-
The detection of the first gravitational wave (GW) from the coalescence of two massive black holes (BHs) by advanced LIGO/Virgo marked the beginning of a new era — the GW astronomy [1]. After 100 years, one of Einstein's crucial predictions was finally confirmed [2]. Following this observation, approximately 90 GW events have been identified by the LIGO/Virgo/KAGRA (LVK) scientific collaborations (see for instance [3−6]). In the future, more advanced ground- and space-based GW detectors will be constructed [7, 8], such as Cosmic Explorer [9], Einstein Telescope [10], LISA [11], TianQin [12, 13], Taiji [14], and DECIGO [15]. These detectors will enable probing signals with a much wider frequency band at larger distances. The advances in this field triggered the interest in the observation of the quasi-normal mode (QNM) of black holes [16], extreme mass ratio inspirals (EMRIs) [17], etc.
In general, GWs emitted during the ringdown stage are studied using the perturbation theory [18, 19]. In general relativity (GR), this theory has been employed extensively in terms of scalar, vector, and tensor (gravitational) perturbations [20]. In fact, the QNMs generated from gravitational perturbations are closely related to the test and confinement of theories of gravity [21]. The resultant QNM frequencies reflect some aspects of the stability of the spacetime under consideration [22]. Simultaneously, the gravitational perturbations on the background fields also play an important role in the stability analysis.
For a spherically symmetric geometry, such a perturbation problem can be divided into odd- and even-parity sectors. In most cases, the latter exhibit a more intricate structure (see for instance [23]). It is important to note that, under the framework of GR, the characters of gravitational perturbations are relatively easy to track (see for instance [24]). However, moving to the realm of modified theories of gravity, the structure of the original action (or equivalently, the Lagrangian) can become sophisticated, which often sets barriers to achieve the desired physical information. One approach to address this problem is to work on the original perturbed Lagrangian and eliminate its non-dynamical terms (according to the degrees of freedom of the theory) before further analysis [16].
Basically, we can substitute the entire background as well as perturbation terms into the original Lagrangian. Treating a perturbation term as a 1st-order infinitesimal quantity allows extracting the 2nd-order part from such a Lagrangian. Subsequently, by using effective mathematical techniques and (probably) introducing suitable gauge invariants, one can (in principle) achieve notable simplification and eliminate all the non-dynamical terms. As a result, it is straightforward to manage the reduced Lagrangian. Such a reduced Lagrangian is crucial for the stability analysis [25−27]. Furthermore, under certain circumstances, this type of stability analysis enables a method to set constraints on a modified theory based on the inherence of its self-consistency [27].
In this study, we investigated the stability of the 2nd-order Lagrangian of a subclass of Horndeski theory under odd-parity gravitational perturbations. As the most general model of scalar-tensor theories, Horndeski theory (and beyond) has recently attracted much attention [25, 28−31]. In Horndeski theory, the action contains a scalar field and the metric tensor field, which give rise to the metric and scalar fields equations with no derivatives beyond the second order. Horndeski theory features the same symmetry as that of GR, including local Lorentz invariance and diffeomorphism [32]. In fact, the stability problem in Horndeski theory has been intensively studied during the past decade [33, 34]. Many typical configurations of the Lagrangian have been investigated. In this study, we focused on a set of specific background solutions of the theory and analyzed the details concerning how the stability is preserved or broken. According to [27], the choice of coupling parameters at the Lagrangian level can affect the criterion for stability analysis in a comprehensive manner. This is demonstrated in this study through analytic background solutions.
The rest of the paper is organized as follows. Sec. II provides the background hairy black hole solutions to the fields in Horndeski theory and demonstrates the corresponding odd-parity perturbations. A notably simplified 2nd-order Lagrangian is obtained from the original one. We present the stability analysis in Sec. III and study how instability emerges. Finally, some concluding remarks are provided in Sec. IV.
In this paper, we adopt a unit system in which
$ c=G=2M=1 $ , where c denotes the speed of light, G is the gravitational constant, and M denotes the total mass of the black hole. All the Greek letters in indices range from 0 to 3. The other usages of indices will be described in due course. -
We consider an action in Horndeski theory with a scalar field denoted by
$ \phi(r) $ [35],$ \begin{aligned}[b] {\cal S} =\;& \int {{\rm d}^4} x \sqrt{-g} \big\{ Q_2(\chi) +Q_3(\chi) \Box \phi + Q_4(\chi) R \\ & +Q_{4, \chi} \big[ (\Box \phi)^2 -\left(\nabla^\mu \nabla^\nu \phi \right) \left(\nabla_\mu \nabla_\nu \phi \right) \big] \big\} ,\; \; \end{aligned} $

(1) where
$ {\chi}\equiv - \frac{1}{2} \nabla^\mu \phi \nabla_\mu \phi, $

(2) and
$ Q_2 = \alpha_{21} \chi + \alpha_{22} (-\chi)^{w_2}, $

(3) $ Q_3 = \alpha_{31} (-\chi)^{w_3}, $

(4) $ Q_4 = \kappa^{-2} + \alpha_{42} (-\chi)^{w_4}, $

(5) with
$ \kappa \equiv \sqrt{8 \pi} $ . For the 4-current to vanish at infinity and considering the finiteness of energy, we set$ \alpha_{21}=\alpha_{31}=0 $ and$ w_2=3 w_4=3/2 $ [35]. The comma in the subscript denotes the derivative with respect to the quantity close to it, R is the Ricci scalar,$ \nabla $ denotes the covariant derivative operator, and the operator$ \Box $ is defined as$ \Box \equiv \nabla^{\mu} \nabla_{\mu} $ .The static and spherically symmetric background metric is expressed in the line-element form as [in the Boyer-Lindquist coordinate
$ (t, r,\theta, \phi) $ ]$ {\rm d} s^2 = -A {\rm d} t^2 + B^{-1} {\rm d} r^2 + r^2 {\rm d}\Omega^2, $

(6) where
${\rm d} \Omega^2$ is the unit two-sphere line element, and A and B are functions of r. Their explicit expressions, together with the background scalar field (denoted by$ \phi_0 $ ), are found to satisfy$ \begin{aligned}[b] & A(r) = B(r) = 1-\frac{1}{r} +\frac{q}{r} \ln r, \\& \phi_0' = \mathfrak{k} \frac{2}{r} \sqrt{-\dfrac{\alpha_{42}}{3 B \alpha_{22}}}, \end{aligned} $

(7) where a prime in the superscript denotes the derivative with respect to r and
$ \mathfrak{k}=\pm 1 $ . The charge q satisfies$ q = (2/3)^{3/2} \kappa^2 \alpha_{42} \sqrt{-\alpha_{42}/\alpha_{22}} $ . Clearly, we must set$\alpha_{42} \cdot \alpha_{22} \leq 0$ .On the basis of the background fields just defined, we are on the position to consider the odd-parity perturbations
1 to them. Note that, given that the scalar field perturbation only has even-parity contributions [39, 40], we only consider the gravitational perturbation for the odd-parity sector.We define the metric as
$ g_{\mu \nu} = {\bar g}_{\mu \nu} + \epsilon h_{\mu \nu} $ , where$ \epsilon $ is a bookkeeping parameter (in contrast, for the scalar field we simply have$ \phi=\phi_0 $ ). The perturbation function$ h_{\mu \nu} $ can be parameterized as [16]$ \begin{array}{*{20}{l}} h_{\mu \nu} &=& \displaystyle\sum\limits_{l=0}^{\infty} \displaystyle\sum\limits_{m=-l}^{l} \begin{pmatrix} 0 & 0 & C_{lm}\csc \theta \partial_\varphi & -C_{lm} \sin \theta \partial_\theta\\ 0 & 0 & J_{lm}\csc \theta \partial_\varphi & -J_{lm} \sin \theta \partial_\theta\\ sym & sym & G_{lm}\csc \theta \big(\cot \theta \partial_\varphi-\partial_\theta \partial_\varphi \big) & sym \\ sym & sym & \dfrac{1}{2} G_{lm}\big(\sin \theta \partial^2_\theta - \cos \theta \partial_\theta- \csc \theta \partial^2_\varphi\big) & - G_{lm} \sin \theta \big(\cot \theta \partial_\phi- \partial_\theta \partial_\varphi \big) \end{pmatrix} Y_{l m}(\theta, \varphi), \\ \end{array} $ 
(8) where
$ C_{lm} $ ,$ J_{lm} $ , and$ G_{lm} $ are functions of t and r, while$ Y_{l m}(\theta, \phi) $ denotes the spherical harmonics. From this point on, we set$ m=0 $ in the above expressions so that$ \partial_\phi Y_{lm}(\theta, \phi)=0 $ . The background has spherical symmetry, and the corresponding linear perturbations do not depend on m [38, 41]. In addition, we adopt the gauge condition$ {G}_{lm}=0 $ (which can be referred to as the RW gauge [38]) in the following, which will set$ C_{lm} $ and$ J_{lm} $ as gauge invariants [16]. For simplicity, we drop the subscript "$ lm $ " in the following to avoid any confusion.By substituting the full metric and scalar field back into the Lagrangian [the integrant of the action described by Eq. (1)], and selecting the
$ {\cal O} (\epsilon^2) $ terms, we obtain$ \begin{aligned}[b] {\cal L}_{\text{odd}} =\;& L\Big( \beta_1 {\dot J}^2 -2 \beta_1 {\dot J} {C^\prime} + \beta_1 \frac{4}{r}{\dot J} C \\ & + \beta_1 {C^{\prime 2}} + \beta_2 J^2 + \beta_3 C^2 \Big), \end{aligned} $

(9) where
$ \begin{aligned}[b] \beta_1 \equiv\;& \frac{1 }{2 \kappa ^2} \sqrt{\frac{B}{A}}, \\ \beta_2 \equiv\;& \frac{A^2}{8 A^{3/2} \kappa ^2 r^2 \phi '} \bigg[8 B^{3/2} \phi '+2 \sqrt{2} B^2 \kappa ^2 \left(4 \alpha _{42} \left(\phi '\right)^2+2 \alpha _{42} r^2 \left(\phi ''\right)^2+\left(\alpha _{22}-2 \alpha _{42}\right) r^2 \left(\phi '\right)^4-2 \alpha _{42} r^2 \phi ^{(3)} \phi '\right) \\ & +\sqrt{2} \alpha _{42} \kappa ^2 r^2 \left(B'\right)^2 \left(\phi '\right)^2-2 \sqrt{2} \alpha _{42} B \kappa ^2 r \phi ' \left(r B'' \phi '+B' \left(r \phi ''+2 \phi '\right)\right)-4 \sqrt{B} L \phi '\bigg] \\ &+ \frac{2 \sqrt{2} \alpha _{42} B^2 \kappa ^2 r^2 \left(A'\right)^2 \left(\phi '\right)^2-A B r \phi ' \left(2 \sqrt{2} \alpha _{42} B \kappa ^2 r A'' \phi '+\sqrt{2} \alpha _{42} \kappa ^2 r A' B' \phi '-8 \sqrt{B} A'\right)}{8 A^{3/2} \kappa ^2 r^2 \phi '}, \\ \beta_3 \equiv\;& \frac{A^2 }{16 A^{5/2} B \kappa ^2 r^2 \phi '} \bigg\{ 2 \sqrt{2} B^2 \kappa ^2 r \left(2 \alpha _{42} r \left(\phi ''\right)^2+\left(\alpha _{22}-2 \alpha _{42}\right) r \left(\phi '\right)^4-4 \alpha _{42} \phi ' \left(r \phi ^{(3)}+2 \phi ''\right)\right) \\ & +8 \sqrt{B} \phi ' \left(L-r B'\right)+\sqrt{2} \alpha _{42} \kappa ^2 r^2 \left(B'\right)^2 \left(\phi '\right)^2 +4 \sqrt{2} \alpha _{42} B \kappa ^2 \phi ' \left[\phi ' \left(r^2 \left(-B''\right)-4 r B'+L\right)-2 r^2 B' \phi ''\right]\bigg\} \\ & +\frac{3 \sqrt{2} \alpha _{42} B^2 \kappa ^2 r^2 A^{\prime 2} \phi^{\prime 2}-4 A B r \phi ' \Big[ \sqrt{2} \alpha _{42} \kappa ^2 r A' B' \phi '+2 \sqrt{B} A'+\sqrt{2} \alpha _{42} B \kappa ^2 \left(r A'' \phi '+A' \left(r \phi ''+2 \phi '\right)\right) \Big]}{16 A^{5/2} B \kappa ^2 r^2 \phi '}, \\ \end{aligned} $ 
(10) $ L\equiv l (l+1) $ ; a dot on a variable denotes time derivative whereas "$ (n) $ '' in the superscript denotes the n-th derivative with respect to r. Note that to obtain Eq. (9), integration by parts [42] and the properties of spherical harmonics [16] have been widely used. Note also that the Lagrangian previously defined can be reduced to that of GR at the$ \alpha_{42}=\alpha_{22}=0 $ limit.According to [27] and introducing a new gauge invariant
$ \zeta \equiv \frac{2}{r} C-C^\prime+{\dot J}, $

(11) the Lagrangian expressed by Eq. (9) becomes
$ \begin{aligned}[b] {\cal L}_{\text{odd}} =\;& L\bigg\{ \beta_1 \left[\zeta^2 -2 \zeta \left( \frac{2}{r} C-C^\prime+{\dot J} \right) \right] \\ & + \beta_2 J^2 + \left( \beta_3-\frac{2}{r^2} \beta_1-\frac{2}{r} \beta_1^\prime \right) C^2 \bigg\},\; \; \; \end{aligned} $

(12) for which the Euler-Lagrange (E-L) equation [43] can be applied on C and J so that their expressions in terms of ζ can be solved. Similar to previous studies, for instance [16] and [27], these solved expressions can be substituted back into Eq. (12), leading to a Lagrangian composed of a single variable ζ (given that non-dynamical terms have been eliminated). Such a Lagrangian can be expressed as
$ {\cal L}_{\text{odd}} = \mathbb{K} {\dot \zeta}^2+\mathbb{G} { \zeta}^{\prime 2}+\mathbb{N} { \zeta}^2. $

(13) To abbreviate the mathematical formulation, we shorten the full expressions of
$ \mathbb{K} $ ,$ \mathbb{G} $ , and$ \mathbb{N} $ . These full expressions can be found in the supplemental material of [44]. The Lagrangian expressed by Eq. (13) is reduced to that of GR at the$ \alpha_{42}=\alpha_{22}=0 $ limit. -
Let us work on the basis of the reduced Lagrangian expressed by Eq. (13). According to [39], the no-ghost stability condition requires
$ \mathbb{K}>0 $ . Using Eq. (7) on$ \mathbb{K} $ , at the point$ r=1 $ it becomes$ \left. \mathbb{K} \right|_{r\to1}= \frac{81 \sqrt{\dfrac{3}{2}} \alpha _{22} \sqrt{-\dfrac{\alpha _{42}}{\alpha _{22}}} L}{64 \pi ^2 \alpha _{42}^2 \left(16 \pi \sqrt{6} \sqrt{-\dfrac{\alpha _{42}}{\alpha _{22}}} \alpha _{42}+9\right){}^2 \mathfrak{k}}. \\ $

(14) Clearly, the no-ghost condition holds only when
${\alpha _{22}} \cdot \mathfrak{k} > 0$ , which implies$ -{\alpha _{42}} \cdot \mathfrak{k} > 0 $ . For later convenience, let us introduce a set of reduced coupling parameters (which are always positive):$ \kappa_{22}\equiv \alpha_{22}/\mathfrak{k} $ and$\kappa_{42}\equiv -\alpha_{42}/\mathfrak{k}$ .According to [27], we define the propagation speed at the radial direction as
$c_r \equiv {\rm d} r_\ast/ {\rm d} t={\hat c}_r/A$ . Here,$ {\hat c}_r $ is a quantity introduced to better describe the radial Laplacian stability condition, which is found to satisfy$ {\hat c}_r^2 \mathbb{K} + \mathbb{G} = 0 $ [27], so that$ {\hat c}_r^2=-\mathbb{G} \cdot \mathbb{K}^{-1} $ . Furthermore, the radial Laplacian stability condition is given by$ {\hat c}_r^2 \geq 0 $ .To monitor the behavior of
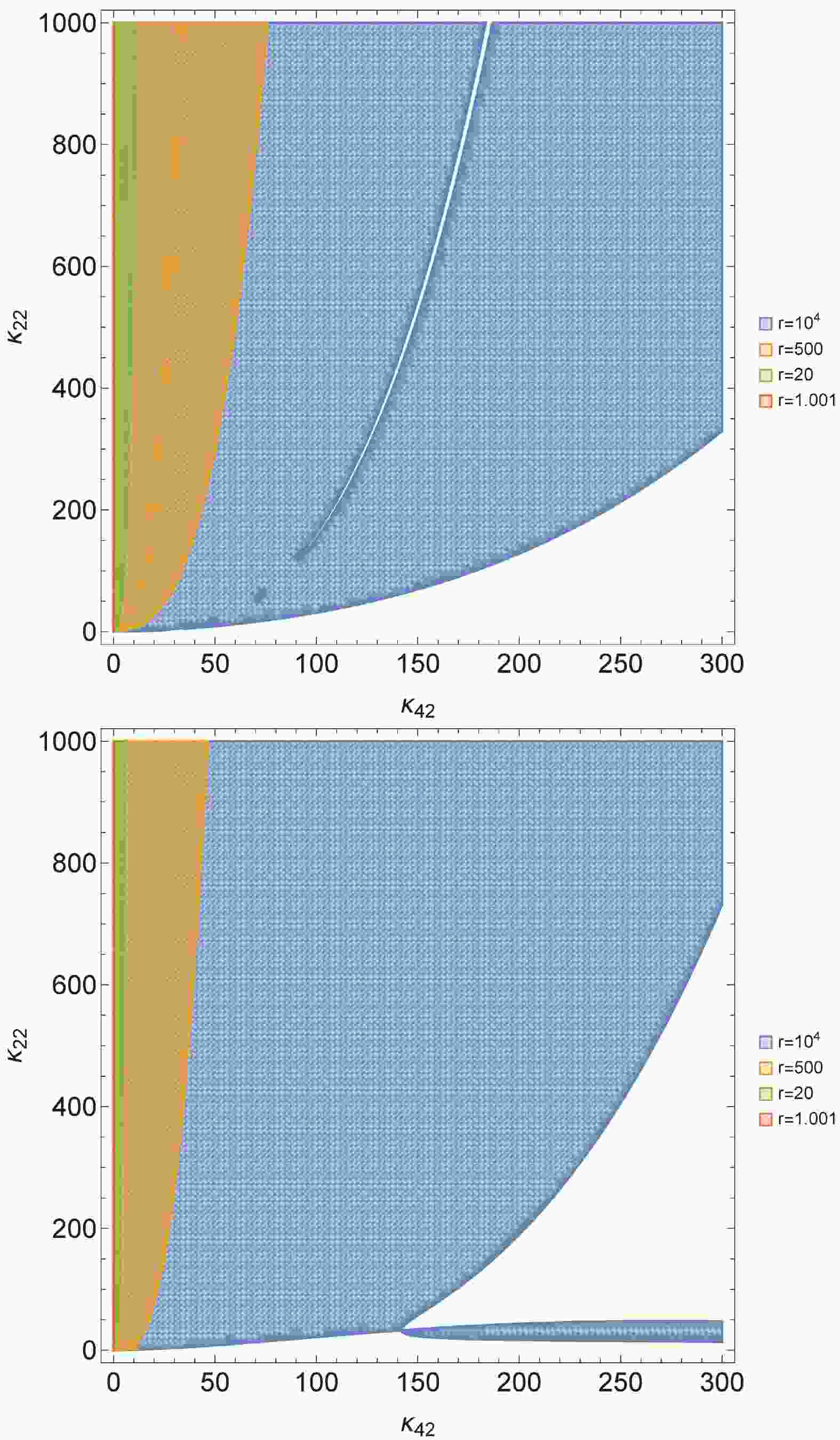
$ {\hat c}_r^2 $ as a function of r, we plotted it out in the phase space of$ (\kappa_{42}, \kappa_{22}) $ by setting$ l=2 $ , as shown in Fig. 1 for various values of r; both cases,$ \mathfrak{k} = \pm 1 $ , are considered. Within the colorful shadowed regions, the radial Laplacian condition, viz.,$ {\hat c}_r^2 \geq 0 $ , is satisfied. In these regions, the quantity$ {\hat c}_r^2 $ is considered at different positions by varying r. Note from Fig. 1 that the "stable region" is shrinking as r approaches the event horizon$ r=1 $ . It is omitted in Fig. 1 that the stable region disappears if r is sufficiently close to$ 1 $ , e.g., when$ r=1+ 10^{-20} $ . This means that this type of instability exists no matter how the coupling parameters are chosen.
Figure 1. Phase space of
$ (\kappa_{42}, \kappa_{22}) $ for which the shadowed regions satisfy$ {\hat c}_r^2 \geq 0 $ , i.e., the radial Laplacian condition is satisfied. The blue, orange, green, and red shadowed regions correspond to$ r=10^4,\;500,\;20,\;1.001 $ , respectively. Upper panel:$ \mathfrak{k} = 1 $ ; lower panel:$ \mathfrak{k} = -1 $ . Here we set$ l=2 $ . Note that only the first quadrant of$ (\kappa_{42}, \kappa_{22}) $ is considered given that$ \kappa_{42} $ and$ \kappa_{22} $ are defined to be positive (cf., Sec. III).For further clarity, let us consider the quantity
$ {\hat c}_r^2 $ in the neighborhood of the event horizon$ r=1 $ (without setting l to a specific value) and insert the full expressions [44]. This leads to$ \begin{aligned}[b] \left. {\hat c}_r^2 \right|_{r \to 1} =\;& -\frac{2}{81} (r-1)^2 \left(16 \sqrt{6} \pi \kappa _{42} \sqrt{\frac{\kappa _{42}}{\kappa _{22}}} \mathfrak{k}-9\right)^2 \\ & + {\cal O}(r-1)^3. \end{aligned} $

(15) Thus, for any combination of the coupling parameters, the radial Laplacian instability always exists in the neighborhood of
$ r=1 $ , as we previously mentioned. This result is consistent with the conclusions drawn in [33−45]2 . -
In this paper, we focused on a specific subclass of Horndeski theory describing the action defined by Eq. (1). Using a set of analytic background solutions expressed by Eq. (7) (with deviations from GR mainly characterized by two coupling parameters), we systematically investigated the odd-parity gravitational perturbation on the background and extracted the 2nd-order Lagrangian of the theory. Applying suitable mathematical techniques, the original Lagrangian was finally reduced to the form expressed by Eq. (13), which presents one degree of freedom, as expected
3 . We further conducted stability analysis (see for instance [25, 27, 39]) and demonstrated how the instability emerges.Certain constraints to the coupling parameters were identified from the no-ghost condition [cf., (14)]. Based on that, the subsequent calculations were simplified. This allows for the calculation and analysis of the radial Laplacian stability condition within the valid phase space of (reduced) coupling parameters (cf., Fig. 1). Figure 1 shows that such a stability condition requires additional constraints to the coupling parameters. More importantly, this stability condition tends to be broken in the neighborhood of the event horizon
$ r=1 $ . Indeed, by using the asymptotic expansion of the criterion$ {\hat c}_r^2 $ [cf., (15)], it is clear that this condition will not be preserved anymore as$ r \to 1 $ [although we observed that such a condition can be satisfied right at the point$ r=1 $ , where$ {\hat c}_r^2(r=1)=0 $ ] is precisely satisfied, no matter how the coupling parameters are chosen. Thus, we conclude that the set of background solutions given by Eq. (7) is not stable and needs to be excluded from the valid solutions, which is consistent with the predictions presented in [34].Setting those coupling parameters to zero (as in the GR limit) in the final criterion or discriminant [cf., (15)] will not always lead to that of GR, departing from what we observed at Lagrangian level. In [27, 45], we observed similar phenomena. This implies that the (in)stability of a theory could be a comprehensive effect and is not necessary for the criterion to behave like a perturbation to the stable GR case. It is also interesting to mention that, according to Fig. 1, the most stringent constraints to the coupling parameters are given by the analysis within the neighborhood of
$ r=1 $ (instead of other positions far from the event horizon). This is similar to the situation described in [39].In the future, we will address other background solutions and models of Horndeski theory. According to [34], we will pay more attention to stable cases. In principle, the corresponding stability analysis can not only help set constraints to the model but also produce a reduced Lagrangian as a byproduct, which can serve for the QNM calculations in the next step. The investigation of more models will facilitate the derivation of some common features according to conclusions from different cases.
-
We would like to express our gratitude to Prof. Anzhong Wang for his valuable comments and suggestions.
Linear instability of hairy black holes in Horndeski theory
- Received Date: 2024-02-29
- Available Online: 2024-07-15
Abstract: Horndeski theory constitutes the most general model of scalar-tensor theories. It has attracted much attention in recent years in relation with black holes, celestial dynamics, stability analysis, etc. It is important to note that, for certain subclasses of Horndeski models, one can obtain analytic solutions for the background fields. This facilitates the investigation of the corresponding stability problems in detail. In particular, we aim to determine the constraints to the model or theory under which the stability conditions can be satisfied. In this study, we focused on a subclass of Horndeski theory and a set of analytic background solutions. In addition, the odd-parity gravitational perturbation and 2nd-order Lagrangian were investigated. Through careful analysis, the instability was identified within the neighborhood of the event horizon. This allows exclusion of a specific geometry for the model. Such an instability is implanted in the structure of the corresponding Lagrangian and is not erased by simply adding numerical constraints on the coupling parameters. As a starting point of our research, the current study provides insights for further exploration of the Horndeski theory.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: