-
The production of heavy quarkonia, including the
$ J/\psi $ meson as the most prominent specimen, provides a perfect laboratory to explore the interplay between perturbative and nonperturbative phenomena in quantum chromodynamics (QCD), given that it accommodates the creation of a heavy quark pair$ Q\bar{Q} $ at high energy as well as its transition into a heavy meson at low energy. The framework of nonrelativistic-QCD (NRQCD) factorization [1] has been successful in explaining the heavy-quarkonium production mechanism. However, the$ J/\psi $ polarization puzzle [2] and other problems in the validation of the predicted universality of the NRQCD long-distance matrix elements (LDMEs) [3, 4] still challenge NRQCD factorization. Shortly after the birth of NRQCD factorization, prompt$ J/\psi $ pair hadroproduction was proposed as a showcase for the color-octet (CO) mechanism, a key feature of NRQCD factorization, because hadroni-zation occurs there twice [5]. Later on, the color-singlet (CS) channel was found to contribute predominately in the region of small and moderate$ J/\psi $ transverse momentum, denoted as$ p_T^{J/\psi} $ [6−9]. Meanwhile, prompt$ J/\psi $ pair hadroproduction is also viewed as a good probe of the double parton scattering (DPS) mechanism in hadron collisions and as a tool to extract its key parameter$ \sigma_{{\rm{eff}}} $ [10]. However, fit results of$ \sigma_{\rm{eff}} $ from experimental [11−14] and theoretical [15, 16] analyses render an incoherent picture.Since the discovery of the Higgs boson at the CERN Large Hadron Collider (LHC) [17, 18], the construction of next-generation
$ e^{+}e^{-} $ colliders that reach center-of-mass energies of hundreds of GeV or even a few TeV for high-precision studies of the electroweak sector of the standard model has been on the agenda of the high-energy physics community. Possible realizations include the CERN Future Circular Lepton Collider (FCC-ee) [19], the Circular Electron Positron Collider (CEPC) [20] in China, and the CERN Compact Linear Collider (CLIC) [21]. As we will argue below, such high-luminosity$ e^{+}e^{-} $ colliders will also offer great opportunities to deepen our understanding of the double prompt$ J/\psi $ production mechanism. A decisive advantage of$ e^{+}e^{-} $ colliders versus hadron colliders resides in the absence of DPS. Historically, inclusive single$ J/\psi $ production in two-photon collisions at the CERN Large Electron Positron Collider (LEP) is among the earliest evidences of the CO mechanism [22, 23].In
$ e^+e^- $ collisions, there are generally two distinct production modes, namely$ e^+e^- $ annihilation and two-photon scattering, where the photons originate from both electromagnetic bremsstrahlung and synchrotron radiation off the colliding bunches known as beamstrahlung. The photons can either directly participate in the hard collision as pointlike particles or as resolved photons via their quark and gluon contents described by photonic parton density functions (PDFs) [24]. This results in three production channels: direct, single resolved, and double resolved.$ J/\psi $ pair production by$ e^{+}e^{-} $ annihilation was investigated by several groups [25−31], even through next-to-next-to-leading order in the strong-coupling constant$ \alpha_s $ [32, 33].$ J/\psi $ pair production by two-photon scattering was first considered by Qiao in 2002 as a contribution to inclusive$ J/\psi $ production [34]. Recently, exclu-sive$ J/\psi $ pair production by two-photon scattering at$ e^{+}e^{-} $ colliders was studied through next-to-leading order (NLO) in$ \alpha_s $ , with the result that QCD corrections, of relative order$ \mathcal{O}(\alpha_s) $ , can decrease theoretical predictions by approximately$ 80\% $ [35].In the charmonium rest frame, the charm quark relative velocity v is not small, being
$ v^2\sim\alpha_s(2m_c) $ , which explains why relativistic corrections, being of relative order$ \mathcal{O}(v^2) $ , may be comparable to QCD corrections. In fact, in$ e^+e^- $ annihilation at center-of-mass energy$ \sqrt{S}=10.6 $ GeV,$ \mathcal{O}(v^2) $ corrections largely enhance the LO predictions for exclusive double charmonium [36] and inclusive$ J/\psi+X_{\rm{non-c\bar{c}}} $ [37, 38] production, and they are also considerable in$ J/\psi $ photo- and hadroproduction, for both yield [39, 40] and polarization [41]. Regarding prompt$ J/\psi $ pair hadroproduction, the$ \mathcal{O}(v^2) $ corrections to the CS channel were found to reduce the cross section appreciably in the large-$ p_T $ region [42] and substantially near threshold [43]. This suggests that$ \mathcal{O}(v^2) $ corrections may also be important in the case of$ J/\psi $ pair production in two-photon scattering, and even further given that$ \mathcal{O}(\alpha_s) $ corrections were found to dramatically reduce the cross section [35], as already mentioned above. This strongly motivates our analysis below. Given that an independent cross check of the results of Ref. [35] is still lacking, we also recalculate the$ \mathcal{O}(\alpha_s) $ corrections here.The rest of this paper is organized as follows. In Sec. II, we describe techniques to calculate the
$ \mathcal{O}(v^2) $ and$ \mathcal{O}(\alpha_s) $ corrections to the short-distance coefficients (SDCs) within the NRQCD factorization framework. In Sec. III, we present numerical predictions appropriate for the FCC-ee, CEPC, and CLIC experimental conditions currently anticipated. In Sec. IV, we summarize our conclusions. -
According to the factorization theorem of the QCD parton model, the differential cross section of inclusive prompt
$ J/\psi $ pair production by two-photon scattering may be expressed as (see, e.g., Ref. [22])$ \begin{aligned}[b] {\rm{d}}\sigma(e^+e^-\to e^+e^-+2J/\psi+X) =\;&\sum\limits_{i,j,H_1,H_2} \int{\rm{d}}x_1{\rm{d}}x_2 f_{\gamma}(x_1)f_{\gamma}(x_2) \int {\rm d} x_i {\rm d} x_j f_{i/\gamma}(x_i)f_{j/\gamma}(x_j) \\ &\times {\rm{d}}\hat{\sigma}(i+j\to H_1+H_2) {\rm{Br}}(H_1 \rightarrow J/\psi+X) {\rm{Br}}(H_2 \rightarrow J/\psi+X)\,, \end{aligned} $ 
(1) where
$ f_{\gamma}(x) $ is the scaled-energy distribution of the photons from both bremsstrahlung and beamstrahlung off the incoming leptons,$ f_{i/\gamma}(x) $ is the PDF in longitudinal-momentum fraction of parton i in the resolved photon, being$ f_{\gamma/\gamma}(x)=\delta(1-x) $ for the direct photon,${\rm{d}}\hat{\sigma} (i+j\to H_1+H_2)$ is the partonic differential cross section for associated production of charmonium states$H_1,H_2=J/\psi, \chi_{cJ},\psi(2S)$ , and$ {\rm{Br}}(H \rightarrow J/\psi+X) $ is the branching fraction of H decay into$ J/\psi $ , being 1 for$ H=J/\psi $ , implying direct production. In Eq. (1), X collectively denotes the undetected particles in the respective final states, reflecting the inclusiveness of the experimental observation mode.At parton level, the Feynman diagrams of
$ 2J/\psi $ production are the same as those of$ J/\psi+c\bar{c} $ production, which was studied for two-photon scattering in Ref. [44], where the single-resolved and double-resolved contributions were found to be greatly suppressed. We recovered this finding at LO for direct$ 2J/\psi $ production in two-photon scattering under FCC-ee experimental conditions, for which we found the single-resolved and double-resolved contributions to be more than three orders of magnitude smaller than the direct contribution. In the following, we concentrate on direct photoproduction. In the latter case, CO contributions are known to be important only at large values of$ p_T^{J/\psi} $ [9], where the cross sections are likely to be too small to be measurable in the first few years of running at the above-mentioned future$ e^+e^- $ colliders. Thus, we particularly focus on CS contributions, which arise from the partonic subprocesses$ \gamma+\gamma\to (c\bar{c})_1({}^3S_1^{[1]})+(c\bar{c})_2({}^3S_1^{[1]})\,, $

(2) $ \gamma+\gamma\to (c\bar{c})_1({}^3P_{J_1}^{[1]})+(c\bar{c})_2({}^3P_{J_2}^{[1]})\,, $

(3) yielding
$ 2J/\psi $ ,$ J/\psi+\psi(2S) $ ,$ 2\psi(2S) $ , and$ \chi_{c_{J1}}+\chi_{c_{J2}} $ final states. We verified that, under FCC-ee experimental conditions, the production rates of the$ \chi_{c_{J1}}+\chi_{c_{J2}} $ channels are approximately one order of magnitude smaller than those of the other channels, and they are reduced by two additional factors of branching fraction to become negligibly small feed-down contributions. We thus concentrate on the partonic subprocess (2) and calculate relativistic corrections of$ \mathcal{O}(v^2) $ and QCD corrections of$ \mathcal{O}(\alpha_s) $ to its cross section. By color conservation, the latter are purely virtual.Through
$ \mathcal{O}(v^2) $ in NRQCD, the relevant partonic cross section appearing in Eq. (1) factorizes as$ \begin{aligned}[b] {\rm{d}}\hat{\sigma}(\gamma+\gamma\to H_1+H_2) =\;&\sum\limits_{m,n,H_1,H_2} \left(\frac{{\rm d} F(m,n)}{m_c^{d_{\mathcal{O}(m)}-4}m_c^{d_{\mathcal{O}(n)}-4}} \langle \mathcal{O}^{H_1}(m)\rangle \langle \mathcal{O}^{H_2}(n)\rangle \right. \\ &+\left.\frac{{\rm d} G_{1}(m,n)}{m_c^{d_{\mathcal{P}(m)}-4}m_c^{d_{\mathcal{O}(n)}-4}} \langle \mathcal{P}^{H_1}(m)\rangle \langle \mathcal{O}^{H_2}(n)\rangle +\frac{d G_{2}(m,n)}{m_c^{d_{\mathcal{O}(m)}-4}m_c^{d_{\mathcal{P}(n)}-4}} \langle \mathcal{O}^{H_1}(m)\rangle \langle \mathcal{P}^{H_2}(n)\rangle \right)\,, \end{aligned} $ 
(4) where
$ m,n={}^{2S+1}L_J^{[a]} $ are quantum numbers in spectroscopic notation, with total spin S, orbital angular momentum L, total angular momentum J, and color configuration$ a=1,8 $ for CS and CO;$ \mathcal{O}^{H}(n) $ and$ \mathcal{P}^{H}(n) $ are four-fermion operators of mass dimensions$ d_{\mathcal{O}} $ and$ d_{\mathcal{P}} $ describing the nonperturbative transition$ n\to H $ at LO and$ \mathcal{O}(v^2) $ ;$ \langle\mathcal{O}^{H}(n)\rangle $ and$ \langle\mathcal{P}^{H}(n)\rangle $ are the respective LDMEs; and$ F(m,n) $ and$ G_i(m,n) $ are the appropriate SDCs. Definitions of the relevant four-fermion operators,$ \mathcal{O}^H({}^3S_1^{[1]}) $ and$ \mathcal{P}^H({}^3S_1^{[1]}) $ , may be found, e.g., in Eq. (3) of Ref. [43]. The calculation of$ F({}^3S_1^{[1]},{}^3S_1^{[1]}) $ and$ G_i({}^3S_1^{[1]},{}^3S_1^{[1]}) $ proceeds in a similar fashion to that of the hadron collider case in Ref. [43] and references cited therein; here, we merely present our final results. Notice that, according to the$ p_T $ power counting rules reported in Ref. [9], we have$ {\rm{d}}\hat{\sigma}/{\rm{d}}p_T^2 \propto 1/p_T^8 $ for partonic subprocess (2).Starting from the Mandelstam variables
$ s=(k_1+k_2)^2 $ ,$ t=(k_1-P_1)^2 $ , and$ u=(k_1-P_2)^2 $ of process$ \gamma(k_1)+\gamma(k_2)\to H_1(P_1)+H_2(P_2) $ , we denote the counterparts of t and u in the nonrelativistic limit as$ t_0 $ and$ u_0 $ , respectively, and define$ \hat{t}_0=t_0+(s-8m_c^2)/2 $ and$ \hat{u}_0=u_0+(s-8m_c^2)/2 $ . The two-body phase space element in the nonrelativistic limit may thus be written as$ {\rm d}\Phi_{20}= \frac{{\rm{d}}\hat{t}_0 {\rm{d}}\hat{u}_0} {8\pi s} \delta\left(\hat{t}_0+\hat{u}_0\right)\,, $

(5) and receives the
$ \mathcal{O}(v^2) $ correction factor$K=-4/(s- 16m_c^2)$ . Our final results then read$ \begin{aligned}[b] \frac{F({^3S_1^{[1]},^3S_1^{[1]}})}{m_c^4}=\;&\frac{1}{2s}\int {\rm d}\Phi_{20} \left(|M_0|^2+|M_1|^2\right)\,, \\ \frac{G_{1}({^3S_1^{[1]},^3S_1^{[1]}})}{m_c^6} =\;&\frac{G_{2}({^3S_1^{[1]},^3S_1^{[1]}})}{m_c^6} \\=\;& \frac{1}{2s}\int {\rm d}\Phi_{20} \left(K|M_0|^2+|N|^2\right)\,, \end{aligned} $

(6) where
$ |M_0|^2 $ is the absolute square of the tree-level am-plitude,$ |M_1|^2 $ denotes its$ \mathcal{O}(\alpha_s) $ correction, and$ |N|^2 $ denotes its$ \mathcal{O}(v^2) $ correction. The expressions for$ |M_0|^2 $ ,$ |M_1|^2 $ , and$ |N|^2 $ assume relatively compact forms when they are expressed in terms of s and$ \hat{t}_0 $ .Below, we present
$ |M_0|^2 $ for reference and$ |N|^2 $ as a new result:$ \begin{aligned}[b] |M_0|^2 =\;& \frac{262144 \pi ^4 \alpha ^2 e_c^4 \alpha _s^2}{729 m_c^2 \left(s^3-4 s \hat{t}_0^2\right)^4} \left[ s^{10} +48 s^9 m_c^2 -16 s^8 \left(\hat{t}_0^2-188 m_c^4\right) -512 s^7 m_c^2 \left(4 m_c^4+\hat{t}_0^2\right) \right. +96 s^6\left(128 \hat{t}_0^2 m_c^4+1024 m_c^8+\hat{t}_0^4\right)\\ & +1536 s^5 \hat{t}_0^2 m_c^2\left(\hat{t}_0^2-16 m_c^4\right) -256 s^4 \left(-3072 \hat{t}_0^2 m_c^8-88 \hat{t}_0^4m_c^4+\hat{t}_0^6\right) +32768 s^3 \hat{t}_0^4 m_c^6 \\ &+\left.256 s^2 \left(128 \hat{t}_0^6 m_c^4 +6144\hat{t}_0^4 m_c^8+\hat{t}_0^8\right) -4096 s \hat{t}_0^6 m_c^2 \left(\hat{t}_0^2 -96m_c^4\right)+49152 \hat{t}_0^8 m_c^4 \right]\,,\quad \end{aligned} $ 
(7) $ \begin{aligned}[b] |N|^2 =\;& -\frac{131072 \pi ^4 \alpha ^2 e_c^4 \alpha _s^2}{2187 m_c^4 \left(s^3-4 s \hat{t}_0^2\right)^5\left(s-16 m_c^2\right)} \left[3 s^{14}-144 s^{13} m_c^2 +s^{12} \left(832 m_c^4-76 \hat{t}_0^2\right) \right. +64 s^{11} \left(55 \hat{t}_0^2 m_c^2-2368 m_c^6\right)\\ &+32 s^{10} \left(-1192 \hat{t}_0^2 m_c^4+82432 m_c^8+25 \hat{t}_0^4\right) -1024 s^9 m_c^2 \left(-2424 \hat{t}_0^2 m_c^4+14336 m_c^8+27 \hat{t}_0^4\right) \\ &-128 s^8 \left(-29184 \hat{t}_0^2 m_c^8-1488 \hat{t}_0^4 m_c^4-1769472 m_c^{12}+35 \hat{t}_0^6\right) +2048 s^7 \hat{t}_0^2 m_c^2 \left(2656 \hat{t}_0^2 m_c^4+50176 m_c^8+47 \hat{t}_0^4\right)\\&+256 s^6 \left(4325376 \hat{t}_0^2 m_c^{12}+98304 \hat{t}_0^4 m_c^8-1184 \hat{t}_0^6 m_c^4+55 \hat{t}_0^8\right) -4096 s^5 \hat{t}_0^4 m_c^2 \left(-4352 \hat{t}_0^2 m_c^4-100352 m_c^8+49 \hat{t}_0^4\right) \end{aligned} $

$ \begin{aligned}[b] \quad\quad &-1024 s^4 \hat{t}_0^4 (-204800 \hat{t}_0^2 m_c^8-272 \hat{t}_0^4 m_c^4-2752512 m_c^{12}+23 \hat{t}_0^6) +16384 s^3 \hat{t}_0^6 m_c^2 (-384 \hat{t}_0^2 m_c^4-75776 m_c^8+27 \hat{t}_0^4) \\ &+16384 s^2 \hat{t}_0^6 (-4352 \hat{t}_0^2 m_c^8-68 \hat{t}_0^4 m_c^4+491520 m_c^{12}+\hat{t}_0^6) -131072 s \hat{t}_0^8 m_c^2 \left(112 \hat{t}_0^2 m_c^4-15360 m_c^8+5 \hat{t}_0^4\right)\\ &\left. +6291456 \hat{t}_0^{10} m_c^4 \left(40 m_c^4+\hat{t}_0^2\right) \right]\,, \end{aligned} $

(8) where α is Sommerfeld's fine-structure constant and
$ e_c=2/3 $ is the fractional electric charge of the charm quark.In the calculation of
$ |M_1|^2 $ , we encountered both ultraviolet (UV) and infrared (IR) divergences, which were both regularized using dimensional regularization with$ D=4-2\epsilon $ space-time dimensions. The UV divergences were removed by renormalizing the parameters and external fields of the tree-level amplitude$ M_0 $ . As usually done in loop computations of heavy-quarkonium production, we adopted the on-mass-shell (OM) scheme for the renormalization of the charm quark wave function ($ Z_2 $ ) and mass ($ Z_m $ ), as well as the gluon wave function ($ Z_3 $ ), and the modified minimal-subtraction ($ \overline{{\rm{MS}}} $ ) scheme for the renormalization of the strong-coupling constant ($ Z_g $ ). For the reader's convenience, we next present the respective one-loop expressions:$ \begin{aligned}[b] \delta Z_2^{{\rm{OS}}} =\;&-C_F\frac{\alpha_s}{4\pi} N_\epsilon \left( \frac{1}{\epsilon_{{\rm{UV}}}} +\frac{2}{\epsilon_{{\rm{IR}}}} +4 \right)+\mathcal{O}(\alpha_s^2)\,,\\ \delta Z_m^{{\rm{OS}}} =\;& -3C_F\frac{\alpha_s}{4\pi} N_\epsilon \left( \frac{1}{\epsilon_{{\rm{UV}}}} +\frac{4}{3} \right)+\mathcal{O}(\alpha_s^2)\,,\\ \delta Z_3^{{\rm{OS}}} =\;& \frac{\alpha_s}{4\pi} N_\epsilon \Bigg[(\beta_0^\prime-2C_A) \left( \frac{1}{\epsilon_{{\rm{UV}}}} -\frac{1}{\epsilon_{{\rm{IR}}}} \right)\\&- \frac{4}{3} T_F(n_f-n_l) \frac{1}{\epsilon_{{\rm{UV}}}}\Bigg]+\mathcal{O}(\alpha_s^2)\,,\\ \delta Z_g^{\overline{{\rm{MS}}}} =\;& -\frac{\beta_0}{2}\, \frac{\alpha_s}{4\pi} N_\epsilon \left( \frac{1}{\epsilon_{{\rm{UV}}}} +\ln\frac{m_c^2}{\mu_r^2} \right)+\mathcal{O}(\alpha_s^2)\,, \end{aligned} $

(9) where
$ N_\epsilon=(4\pi\mu_r^2/m_c^2)^\epsilon/\Gamma(1-\epsilon) $ ,$ \mu_r $ is the renormalization scale,$ \beta_0=11C_A/3-4T_Fn_f/3 $ is the one-loop coefficient of the QCD beta function,$ C_A=3 $ ,$ T_F=1/2 $ ,$ n_f=4 $ is the number of active quark flavors, and$ \beta_0^\prime $ emerges from$ \beta_0 $ by replacing$ n_f $ with the number of light quark flavors$ n_l=3 $ . Thanks to the absence of real gluon radiation, the IR singularities in$ |M_1|^2 $ cancel each other in combination with the IR divergences from wave function renormalization in Eq. (9). Our result for$ |M_1|^2 $ is too lengthy to be included here. We found numerical agreement with the results for double charmonium photoproduction in Ref. [35] upon adopting the inputs specified there. Looking at the one-loop diagrams in Fig. 2 of Ref. [35], we note that all of them scale with$ e_c^2 $ except for the box diagrams in Fig. 2(l), which scale with$ e_q^2 $ . Keeping this in mind, our analytic results readily carry over to double bottomonium production.1 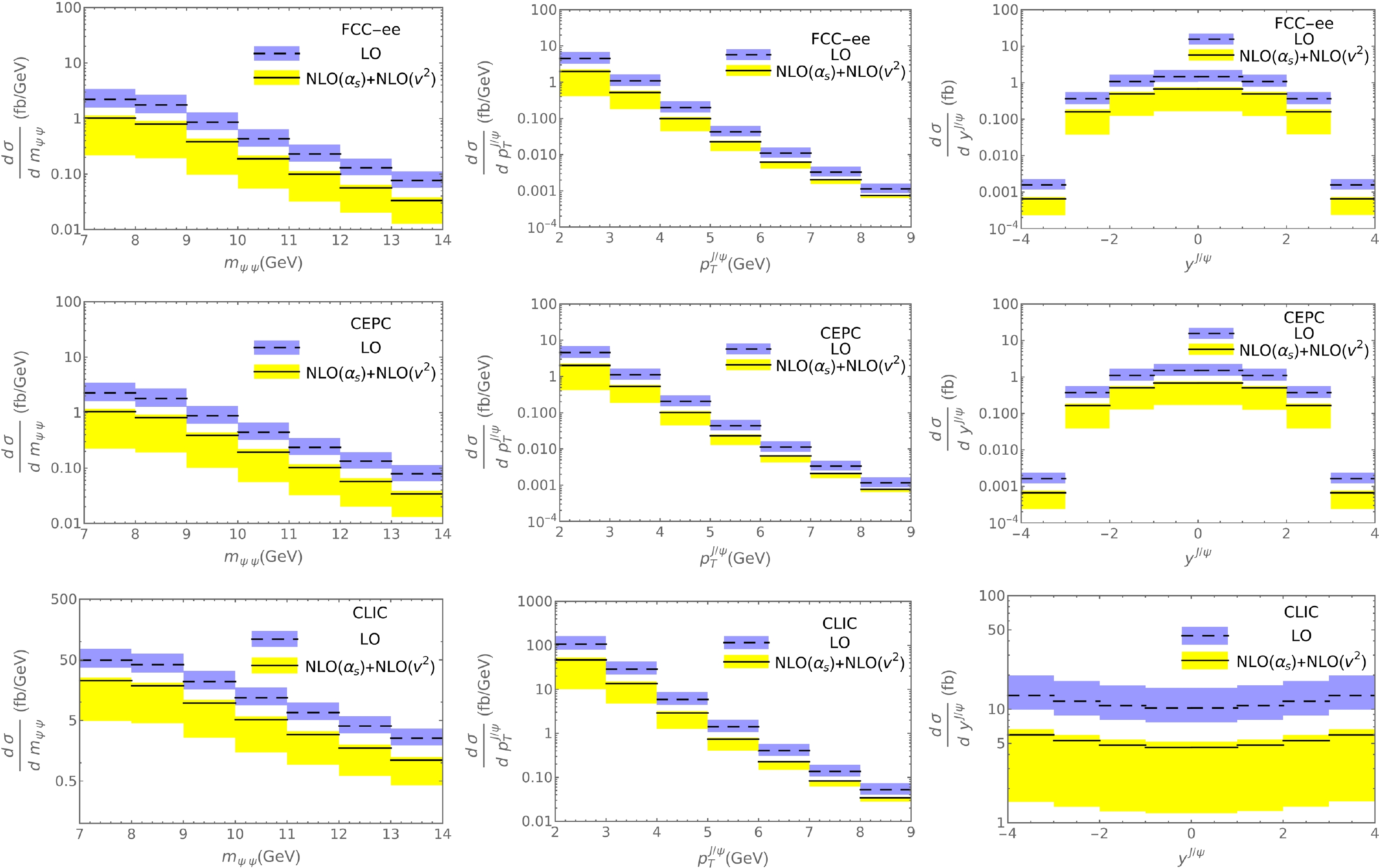
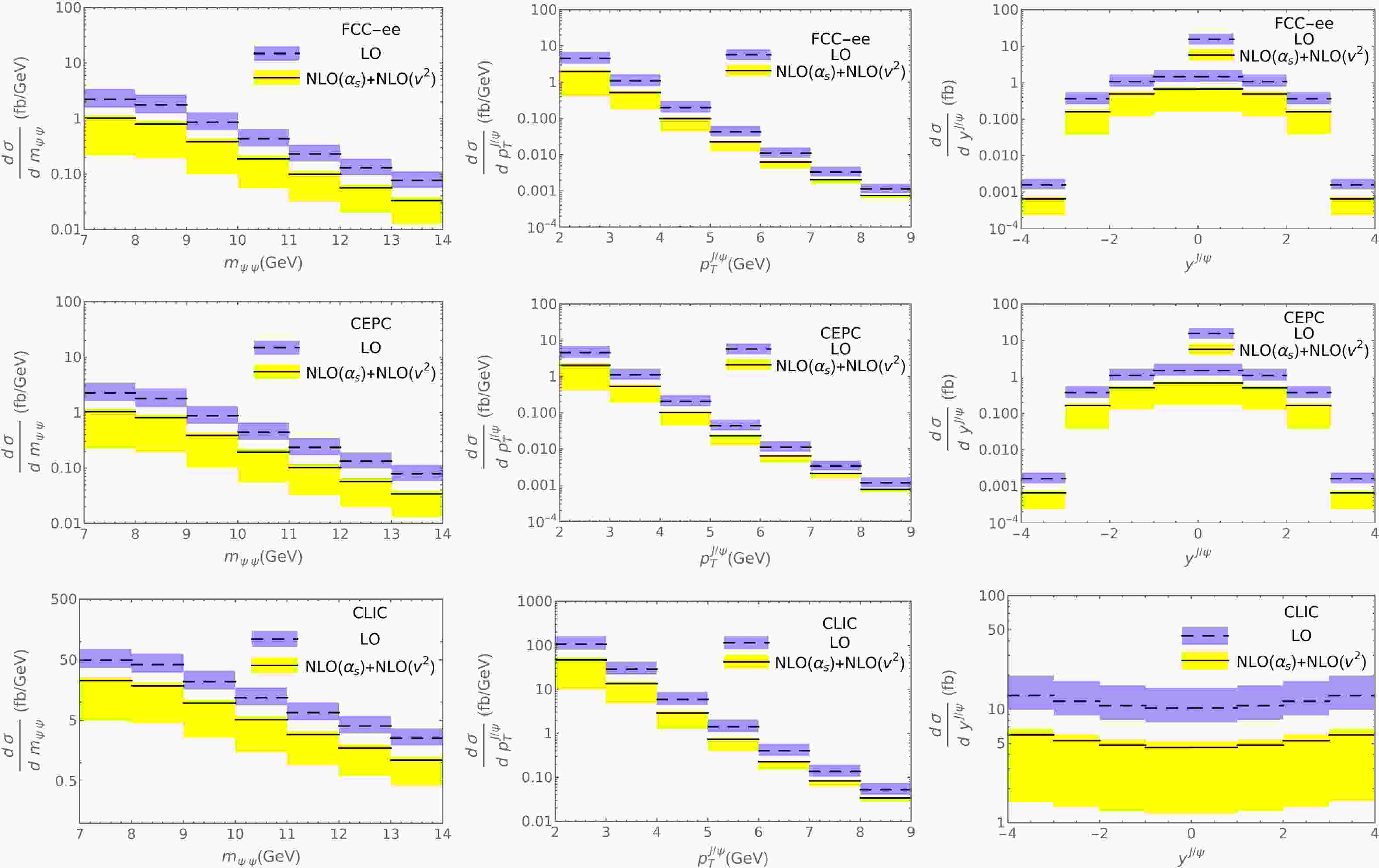
Figure 2. (color online) LO and full NLO NRQCD predictions of
$ {\rm{d}}\sigma/{\rm{d}}m_{\psi \psi} $ [fb/GeV] (left),$ {\rm{d}}\sigma/{\rm{d}}p_T^{J/\psi} $ [fb/GeV] (center), and$ {\rm{d}}\sigma/{\rm{d}}y^{J/\psi} $ [fb] (right) for$ e^+e^-\to 2J/\psi+X $ via photoproduction at FCC-ee (top), CEPC (center), and CLIC (bottom). The theoretical uncertainties at LO and NLO are indicated by the shaded blue and yellow bands, respectively.We used the program packages FeynArts [45] and QGRAF [46] to generate Feynman diagrams and am-plitudes, and FeynCalc [47] and FORM [48] to handle the Dirac and SU(3)
$ {}_c $ algebras. We reduced the one-loop scalar integrals to a small set of master integrals using the Laporta algorithm [49] of integration by parts [50] as implemented in the program packages Reduze 2 [51] and FIRE6 [52]. We evaluated the master integrals analyti-cally using the program packages Package-X 2.0 [53] and QCDloop [54]. -
In the numerical analysis conducted, we evaluated
$ \alpha_s^{(n_f)}(\mu_r) $ with$ n_f=4 $ and$ \Lambda_{\rm{QCD}}^{(4)}=215\; {\rm{MeV}} $ (326 MeV) at tree level (one loop) [55]. We set$ \mu_r=\xi\sqrt{s} $ , with$ \xi=1 $ as default value, and varied ξ between 1/2 and 2 to estimate the theoretical uncertainties from unknown higher orders in$ \alpha_s $ . For the sake of definiteness, we set$ m_c=1.5\; {\rm{GeV}} $ , as frequently done in similar analyses, thereby facilitating comparisons with related results reported in the literature. The values$ m_{J/\psi}=3.097\; {\rm{GeV}} $ ,$ m_{\psi(2S)}=3.686\; {\rm{GeV}} $ , and$ {\rm{Br}}(\psi(2S) \rightarrow J/\psi+X)=61.4\% $ for masses and branching fraction, respectively, were taken from the latest Review of Particle Physics [56]. Concerning the$ J/\psi $ and$ \psi(2S) $ CS LDMEs, we used the values evaluated from the wave functions at the origin for the Buchmüller-Tye potential [57],$ \begin{aligned}[b] \langle \mathcal{O}^{J/\psi}({}^3S_1^{[1]})\rangle &=1.16\; {\rm{GeV}}^3\,, \\ \langle \mathcal{O}^{\psi(2S)}({}^3S_1^{[1]})\rangle &=0.758\; {\rm{GeV}}^3\,, \end{aligned} $

(10) and estimated the values of
$ \mathcal{O}(v^2) $ using the ratio obtained for the$ J/\psi $ case in Ref. [58],$ \frac{\langle \mathcal{P}^{J/\psi}({}^3S_1^{[1]})\rangle} {\langle \mathcal{O}^{J/\psi}({}^3S_1^{[1]} \rangle} = 0.5\; {\rm{GeV}}^2\approx \frac{\langle \mathcal{P}^{\psi(2S)}({}^3S_1^{[1]})\rangle} {\langle\mathcal{O}^{\psi(2S)}({}^3S_1^{[1]})\rangle}\,. $

(11) In the evaluation of feed-down contributions to differential cross sections, we approximated the momentum of the
$ J/\psi $ meson from$ \psi(2S) $ decay as$ p_{J/\psi} = \frac{m_{J/\psi}}{m_{\psi(2S)}}p_{\psi(2S)}\,. $

(12) We included both bremsstrahlung and beamstrahlung by superimposing their spectra. The bremsstrahlung distribution is described in the Weizsäcker-Williams approximation (WWA) as [59]
$ f^{{\rm{WWA}}}_{\gamma}(x) = \frac{\alpha}{2\pi} \left[ \frac{1+(1-x)^2}{x} \ln\frac{Q_{\rm{max}}^2}{Q_{\rm{min}}^2} + 2m_e^2x \left( \frac{1}{Q_{\rm{max}}^2}-\frac{1}{Q_{\rm{min}}^2} \right) \right]\,, $

(13) with photon virtuality
$ Q^2 $ bounded by$ \begin{aligned}[b] Q_{\rm{min}}^2 &= \frac{m_e^2x^2}{1-x}\,, \\ Q_{\rm{max}}^2 &=E_e^2\theta_c^2(1-x) +Q_{\rm{min}}^2\,, \end{aligned} $

(14) where
$ x=E_\gamma/E_e $ ,$ E_e=\sqrt{S}/2 $ is the incoming-lepton energy,$ E_\gamma $ is the radiated-photon energy, and$ \theta_c $ is the maximum angle by which the photon is deflected from the flight direction of the emitting lepton in the center-of-mass frame. The x distribution of beamstrahlung is characterized by the effective beamstrahlung parameter$\Upsilon $ . If$ \Upsilon \lesssim 5 $ , a useful and convenient approximation is given by [60]$ \begin{aligned}[b] f^{{\rm{beam}}}_{\gamma}(x)=\;&\frac{1}{\Gamma(1/3)}\left(\frac{2}{3\Upsilon}\right)^{1/3}x^{-2/3}(1-x)^{-1/3} {\rm e}^{-2x/[3\Upsilon(1-x)]}\\ &\times\Bigg\{\frac{1-\sqrt{\Upsilon/24}}{g(x)}\left[1-\frac{1}{g(x)N_\gamma}\right]\left(1-{\rm e}^{-g(x)N_{\gamma}}\right)\\&+\sqrt{\frac{\Upsilon}{24}}\left[1-\frac{1}{N_\gamma}\left(1-{\rm e}^{-N_\gamma}\right)\right]\Bigg\}\,, \end{aligned} $

(15) where
$ g(x)=1-\frac{1}{2}\left[(1+x)\sqrt{1+\Upsilon^{2/3}}+1-x \right](1-x)^{2/3}\,, $

(16) and
$ N_\gamma=\frac{5\alpha\sigma_zm_e^2\Upsilon}{2E_e\sqrt{1+\Upsilon^{2/3}}} $

(17) is the average number of photons emitted by an electron or position during the collision, with
$ \sigma_z $ being the longi-tudinal bunch length.As mentioned in Sec. I, we assessed three future realizations of high-energy, high-luminosity
$ e^+e^- $ colliders under discussion by the worldwide particle physics community, namely FCC-ee [19], CEPC [20], and CLIC [21], with regard to their potentials to allow for measurements of prompt$ J/\psi $ pair photoproduction. For each of them, Table 1 presents the set of parameters relevant for our numerical analysis, including$ e^+e^- $ center-of-mass energy$ \sqrt{S} $ , upper cut$ \theta_c $ on bremsstrahlung deflection angle, average beamstrahlung parameter$\Upsilon $ , longitudinal bunch length$ \sigma_z $ , and estimated luminosity per experiment$ \int{\rm{d}}t\,\mathcal{L} $ integrated over one year of running, as reported in Ref. [56]. Throughout our study, we imposed the cut$ p_T^{J/\psi}\ge2\; {\rm{GeV}} $ on the transverse momentum of each$ J/\psi $ meson.facility $ \sqrt{S} $ /GeV

$ \theta_c $ /mrad

average $\Upsilon $ 

$ \sigma_z $ /mm

$ \int{\rm{d}}t\,\mathcal{L}/\rm ab^{-1} $ 

FCC-ee 92 30 $ 10^{-4} $ 

15.5 17 CEPC 92 33 $ 2\times10^{-4} $ 

8.7 15 CLIC 3,000 20 5 0.044 0.6 Table 1. Parameters of FCC-ee, CEPC, and CLIC relevant for our calculations.
We started by considering the total cross section
$ \sigma(e^+e^-\to 2J/\psi+X) $ via photoproduction. Starting from the LO NRQCD predictions, we added the$ \mathcal{O}(v^2) $ and$ \mathcal{O}(\alpha_s) $ corrections in turn. Our results for FCC-ee, CEPC, and CLIC are displayed in Table 2, where the central values refer to$ \xi=1 $ and the theoretical error bands to$ \xi=1/2,2 $ . In all three cases, we observe that the$ \mathcal{O}(v^2) $ corrections induce a reduction by approximately 12% and the$ \mathcal{O}(\alpha_s) $ corrections induce a further reduction by approximately 49%, adding up to a total reduction by approximately 55%. To judge the phenomenological significance of the$ \mathcal{O}(v^2) $ corrections in view of the status quo, we must rather compare them to the$ \mathcal{O}(\alpha_s) $ -corrected re-sults [35], in which case the reduction is as large as$ 17^{+39}_{-6} $ %. Regarding theoretical uncertainties, we observe from Table 2 that their absolute sizes are reduced whenever$ \mathcal{O}(v^2) $ or$ \mathcal{O}(\alpha_s) $ corrections are included. Contrary to naïve expectations, the relative uncertainty is slightly increased upon inclusion of the$ \mathcal{O}(\alpha_s) $ corrections. This is because of the abnormally large reductions of the central predictions under the influence of the$ \mathcal{O}(v^2) $ and$ \mathcal{O}(\alpha_s) $ corrections.order FCC-ee CEPC CLIC LO $ 5.88^{+2.99}_{-1.70} $ 

$ 6.00^{+3.06}_{-1.73} $ 

$ 144^{+73}_{-36} $ 

plus $ \mathcal{O}(v^2) $ 

$ 5.17^{+2.64}_{-1.49} $ 

$ 5.28^{+2.69}_{-1.53} $ 

$ 126^{+64}_{-32} $ 

plus $ \mathcal{O}(\alpha_s) $ 

$ 2.65^{+0.34}_{-1.99} $ 

$ 2.71^{+0.34}_{-2.03} $ 

$ 64.6^{+7.5}_{-47.9} $ 

Table 2. NRQCD predictions of
$ \sigma(e^+e^-\to 2J/\psi+X) $ [fb] via photoproduction, at LO and with$ \mathcal{O}(v^2) $ and$ \mathcal{O}(\alpha_s) $ corrections consecutively added, at FCC-ee, CEPC, and CLIC along with the corresponding theoretical uncertainties.Experimentally,
$ J/\psi $ mesons may be most easily detected and reconstructed through their decays to$ e^+e^- $ and$ \mu^+\mu^- $ pairs, with a combined branching fraction of$ {\rm{Br}}(J/\psi\rightarrow l^+l^-)=12\% $ [56]. Dressing the final predictions in Table 2 with two factors of$ {\rm{Br}}(J/\psi\rightarrow l^+l^-) $ and the respective integrated luminosities$ \int {\rm{d}}t\,\mathcal{L} $ per experiment from Table 1, we obtained$ 649^{+82}_{-488} $ ,$ 584^{+75}_{-439} $ , and$ 558^{+64}_{-414} $ signal events per year at FCC-ee, CEPC, and CLIC, respectively.We then turned our attention to cross section distributions in the
$ J/\psi $ pair invariant mass$ m_{\psi\psi} $ as well as transverse momentum$ p_T^{J/\psi} $ , and rapidity$ y^{J/\psi} $ of any$ J/\psi $ meson. Specifically, we considered the ranges$7\; {\rm{GeV}}\le m_{\psi\psi}\le 14\; {\rm{GeV}}$ ,$ 2\; {\rm{GeV}}\le p_T^{J\psi}\le 9\; {\rm{GeV}} $ , and$ -4\le y^{J/\psi}\le 4 $ in bins of unit length, yielding 7, 7, and 8 bins, respectively.To obtain a more detailed picture of the sizes of corrections and theoretical uncertainties, we studied the two consecutive correction factors
$ K_{\alpha_s}={\rm{d}}\sigma^{\mathcal{O}(\alpha_s)}/{\rm{d}}\sigma^{{\rm{LO}}} $ and$ K_{v^2}={\rm{d}}\sigma^{\mathcal{O}(\alpha_s,v^2)}/{\rm{d}}\sigma^{\mathcal{O}(\alpha_s)} $ . For this purpose, we concentrate on the FCC-ee case because the differences with respect to the CEPC and CLIC cases largely cancel out in the ratios. Our NRQCD predictions for$ K_{\alpha_s} $ and$ K_{v^2} $ are presented in Fig. 1. We observe from Fig. 1 that the central values of$ K_{\alpha_s} $ range from 0.55 to 0.75 in the$ m_{\psi\psi} $ ,$ p_T^{J/\psi} $ , and$ y^{J/\psi} $ ranges considered; the$ m_{\psi\psi} $ and$ |y^{J/\psi}| $ distributions monotonically increase, and so does the$ p_T^{J/\psi} $ distribution beyond$ p_T^{J/\psi}=4\; {\rm{GeV}} $ . Figure 1 also shows that$ K_{v^2} $ ranges from 0.6 to 0.9 and features$ m_{\psi\psi} $ ,$ p_T^{J/\psi} $ , and$ y^{J/\psi} $ line shapes that behave inversely to$ K_{\alpha_s} $ . In particular, the relativistic corrections are most important at large values of$ m_{\psi\psi} $ and$ |y^{J/\psi}| $ , as well as at small values of$ p_T^{J/\psi} $ . We conclude that the overall correction factor$K={\rm{d}}\sigma^{\mathcal{O}(\alpha_s,v^2)}/{\rm{d}}\sigma^{{\rm{LO}}} =K_{\alpha_s}K_{v^2}$ exhibits a strongly reduced variation with$ m_{\psi\psi} $ ,$ p_T^{J/\psi} $ , and$ y^{J/\psi} $ .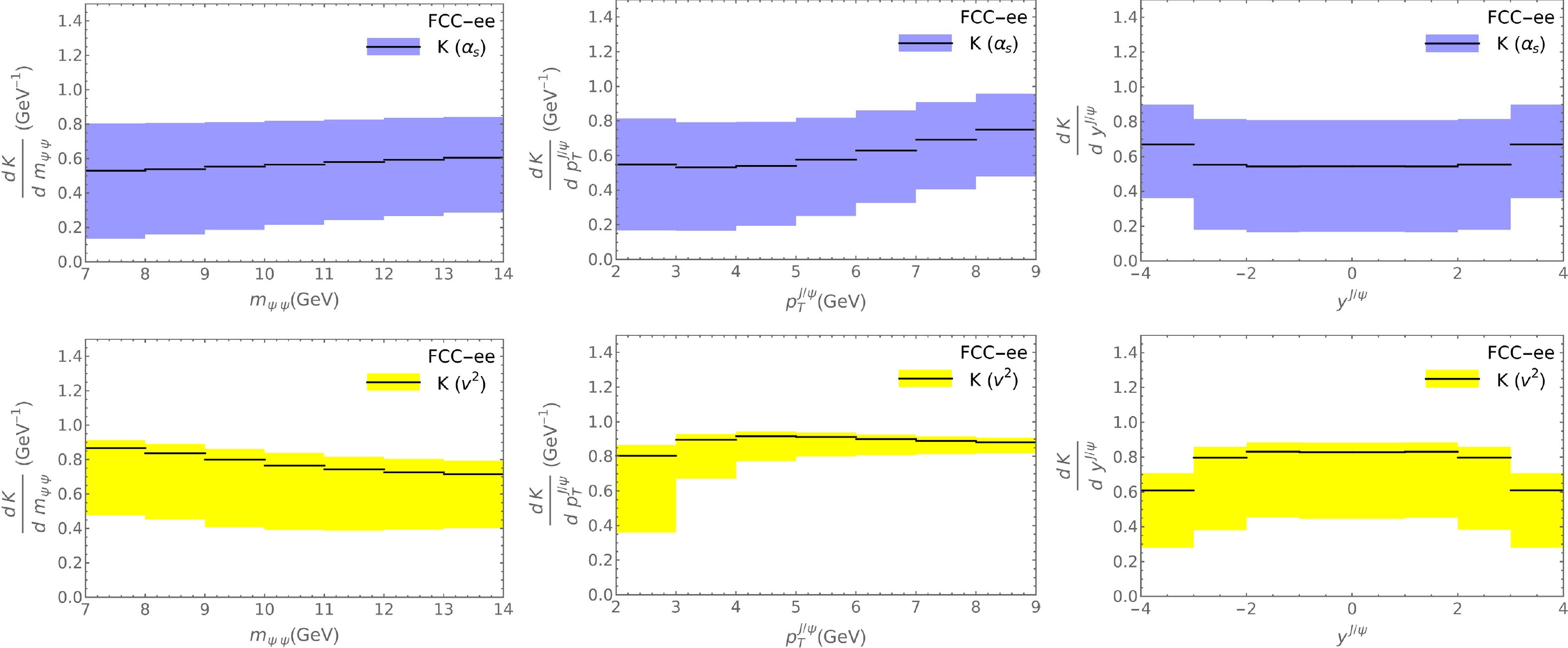
Figure 1. (color online) NRQCD predictions of
$ m_{\psi \psi} $ (left),$ p_T^{J/\psi} $ (center), and$ y^{J/\psi} $ (right) distributions of$ K_{\alpha_s} $ (top) and$ K_{v^2} $ (bottom) at FCC-ee. The theoretical uncertainties in$ K_{\alpha_s} $ and$ K_{v^2} $ are indicated by the shaded blue and yellow bands, respectively.In Fig. 2, we present binned
$ m_{\psi\psi} $ ,$ p_T^{J/\psi} $ , and$ y^{J/\psi} $ distributions of$ e^+e^-\to 2J/\psi+X $ via photoproduction in NRQCD at LO and full NLO, including both$ \mathcal{O}(v^2) $ and$ \mathcal{O}(\alpha_s) $ corrections, for the FCC-ee, CEPC, and CLIC experimental setups. We observe from Fig. 2 that the K factors vary only slightly with$ m_{\psi\psi} $ and$ y^{J/\psi} $ and moderately with$ p_T^{J/\psi} $ , as expected from the above discussion of Fig. 1. In fact, taking FCC-ee again as a representative example, we have$ K=045_{-0.37}^{+0.26} $ for the$ m_{\psi\psi} $ and$ y^{J/\psi} $ distributions, except for bins 1 and 8 of the latter, where$ K=0.41_{-0.30}^{+0.23} $ . For the$ p_T^{J/\psi} $ distribution, the K factor ranges from$ 0.44_{-0.38}^{+0.27} $ in the first bin up to$ 0.66_{-0.27}^{+0.21} $ in the last bin.The respective numbers of signal events per year, based on our best predictions, are collected in Table 3. For the three experimental setups, promising yields are expected in the lower
$ m_{\psi\psi} $ and$ p_T^{J/\psi} $ ranges and in the central$ y^{J/\psi} $ region.bin 1 2 3 4 5 6 7 8 $ m_{\psi\psi} $ 

$ 250^{+30}_{-197} $ 

$ 195^{+25}_{-148} $ 

$ 93.5^{+12.4}_{-70.0} $ 

$ 46.1^{+6.5}_{-32.9} $ 

$ 24.4^{+3.4}_{-16.7} $ 

$ 13.8^{+1.9}_{-8.9} $ 

$ 8.17^{+1.09}_{-5.05} $ 

– $ p_T $ 

$ 486^{+66}_{-386} $ 

$ 128^{+14}_{-83} $ 

$ 24.4^{+2.3}_{-13.7} $ 

$ 5.56^{+0.38}_{-2.49} $ 

$ 1.53^{+0.07}_{-0.52} $ 

$ 0.501^{+0.010}_{-0.124} $ 

$ 0.185^{+0.001}_{-0.032} $ 

– y $ 0.159^{+0.023}_{-0.102} $ 

$ 39.4^{+5.3}_{-30.2} $ 

$ 121^{+15}_{-90} $ 

$ 164^{+21}_{-123} $ 

$ 164^{+21}_{-123} $ 

$ 121^{+15}_{-90} $ 

$ 39.4^{+5.3}_{-30.1} $ 

$ 0.159^{+0.023}_{-0.102} $ 

$ m_{\psi\psi} $ 

$ 225^{+27}_{-177} $ 

$ 176^{+23}_{-134} $ 

$ 84.2^{+11.0}_{-62.3} $ 

$ 41.6^{+5.8}_{-29.6} $ 

$ 22.0^{+3.1}_{-15.0} $ 

$ 12.4^{+1.7}_{-8.1} $ 

$ 7.37^{+0.98}_{-4.55} $ 

– $ p_T $ 

$ 438^{+59}_{-347} $ 

$ 115^{+13}_{-75} $ 

$ 22.0^{+2.1}_{-12.3} $ 

$ 5.01^{+0.35}_{-2.25} $ 

$ 1.38^{+0.06}_{-0.47} $ 

$ 0.452^{+0.010}_{-0.112} $ 

$ 0.167^{+0.001}_{-0.029} $ 

– y $ 0.144^{+0.021}_{-0.093} $ 

$ 35.5^{+4.8}_{-27.2} $ 

$ 109^{+14}_{-81} $ 

$ 147^{+19}_{-110} $ 

$ 147^{+19}_{-111} $ 

$ 109^{+14}_{-81} $ 

$ 35.6^{+4.8}_{-27.2} $ 

$ 0.144^{+0.021}_{-0.093} $ 

$ m_{\psi\psi} $ 

$ 197^{+22}_{-154} $ 

$ 162^{+20}_{-123} $ 

$ 83.8^{+10.7}_{-61.6} $ 

$ 44.4^{+5.8}_{-31.5} $ 

$ 25.2^{+3.3}_{-17.2} $ 

$ 15.1^{+2.0}_{-9.9} $ 

$ 9.61^{+1.18}_{-5.93} $ 

– $ p_T $ 

$ 407^{+50}_{-319} $ 

$ 118^{+13}_{-77} $ 

$ 25.2^{+2.4}_{-14.2} $ 

$ 6.39^{+0.46}_{-2.95} $ 

$ 1.97^{+0.08}_{-0.69} $ 

$ 0.718^{+0.016}_{-0.184} $ 

$ 0.296^{+0.002}_{-0.053} $ 

– y $ 51.5^{+6.2}_{-38.3} $ 

$ 45.9^{+5.5}_{-34.0} $ 

$ 41.9^{+5.0}_{-31.0} $ 

$ 39.9^{+4.8}_{-29.4} $ 

$ 40.0^{+4.8}_{-29.5} $ 

$ 41.9^{+5.0}_{-30.9} $ 

$ 45.9^{+5.5}_{-33.9} $ 

$ 51.4^{+6.2}_{-38.1} $ 

Table 3. Numbers of expected signal events per year in each bin of
$ m_{\psi \psi} $ ,$ p_T^{J/\psi} $ , and$ y^{J/\psi} $ at FCC-ee (top), CEPC (center), and CLIC (bottom).We are faced by considerable theoretical uncertainties in Tables 2 and 3 and Figs. 1 and 2, which manifest themselves in sizable shifts under
$ \mu_r $ variations. While we believe that our default choice$ \mu_r=\sqrt{s} $ for the renormalization scale is most appropriate for the problem considered, it is instructive to also consider alternatives. In the case of$ J/\psi $ single or associated production, the$ J/\psi $ transverse mass$ m_T=\sqrt{p_T^2+4m_c^2} $ is often chosen as the default value. This motivates us to explore the choice$ \mu_r=\xi m_T $ with$ \xi=1/2,1,2 $ . We do this by taking$ {\rm{d}}\sigma/{\rm{d}}p_T $ at FCC-ee as an example; our full NLO NRQCD predictions are presented in Table 4. These turn out to be considerably smaller than our default predictions in Fig. 2 and even partly negative, which disqualifies this low scale choice altogether.bin 1 2 3 4 5 6 7 $ \xi=1/2 $ 

$ -9.42 $ 

$ -1.90 $ 

$ -0.272 $ 

$ -0.0430 $ 

$ -0.00726 $ 

$ -0.00120 $ 

$ -0.000124 $ 

$ \xi=1 $ 

$ -0.162 $ 

0.0673 0.0270 0.00974 0.00370 0.00148 0.000620 $ \xi=2 $ 

1.81 0.519 0.0100 0.023 0.00647 0.00213 0.000790 Table 4. Full-NLO NRQCD predictions of
$ {\rm{d}}\sigma/{\rm{d}}p_T $ [fb/GeV] at FCC-ee for$ \mu_r=\xi m_T $ . -
A tantalizing aspect of the physics potentials of future high-energy, high-luminosity
$ e^+e^- $ colliders is to shed light on the mechanism underlying the formation of heavy quarkonia.$ J/\psi $ pair production, which has been extensively studied at LHC, provides a particularly sen-sitive probe for that. While the hadroproduction of$ J/\psi $ pairs is widely affected by sizable but poorly known DPS contributions [10], the latter are absent in$ e^+e^- $ collisions. This motivated us to study prompt$ J/\psi $ pair production in two-photon collisions at future$ e^+e^- $ colliders considering the FCC-ee [19], CEPC [20], and CLIC [21] experimen-tal setups. We derived, for the first time, the relativistic corrections of$ \mathcal{O}(v^2) $ from both matrix elements and phase space, providing an independent check of the quantum corrections of$ \mathcal{O}(\alpha_s) $ presented in numerical form in Ref. [35]. We found that the familiar$ \mathcal{O}(\alpha_s) $ reduction [35] is significantly amplified by the$ \mathcal{O}(v^2) $ corrections. In fact, the$ \mathcal{O}(\alpha_s) $ -corrected results are typically reduced by 20%. Thanks to the extremely high luminosities envisaged at the future$ e^+e^- $ facilities, promising signal yields may still be expected. Assuming that the$ J/\psi $ mesons are reconstructed via their$ e^+e^- $ and$ \mu^+\mu^- $ decays, we predict$ 649^{+82}_{-488} $ ,$ 584^{+75}_{-439} $ , and$ 558^{+64}_{-414} $ signal events per year at the FCC-ee, CEPC, and CLIC, respectively. The large theo-retical uncertainties are due to the lack of knowledge of higher-order corrections and determined by variations of the renormalization scale, as usual. As a by-product, our results can easily be applied to double$ J/\psi $ production in ultra-peripheral collisions at hadron colliders. -
We thank Cong-Feng Qiao for helpful communications enabling a comparison with the results of Ref. [35].
Next-to-leading-order relativistic and QCD corrections to prompt $ {\boldsymbol J/\boldsymbol\psi} $ pair photoproduction at future ${\boldsymbol e^{\bf +}\boldsymbol e^{\bf -}} $ colliders
- Received Date: 2024-02-27
- Available Online: 2024-08-15
Abstract: Within the framework of nonrelativistic-QCD factorization, we calculate both the next-to-leading-order relativistic and QCD corrections to prompt








 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: