-
Recently, an extension of the interacting boson model with
${S U}(3)$ higher-order interactions (SU3-IBM for short) was proposed to describe the spherical-like γ-soft spectra of 110Cd [1], explain the puzzling$ B(E2) $ anomaly [2, 3], discuss the prolate-oblate asymmetric shape phase transition in the Hf-Hg region including 196Pt [4], and provide an$E(5)$ -like description for 82Kr [5].${O}(6)$ higher-order interactions were found to be unable to explain the$ B(E2) $ anomaly [6]. These results imply that the${S U}(3)$ symmetry dominates the quadrupole deformation of a nucleus, and the γ-softness in realistic nuclei may be an emergent phenomenon, having a deep relationship with the${SU}(3)$ symmetry.The Cd puzzle [7] is the main motivation for proposing the SU3-IBM [1]. The normal states of the Cd isotopes exhibit a new spherical-like γ-soft rotational behavior (the spectra are similar to the phonon excitation of the spherical shape, whereas the transitional rates are similar to the γ-soft rotation), which is unexpected in standard nuclear structure studies [8−14]. The key observation is that no
$ 0_{3}^{+} $ state exists at the three phonon level [10, 13, 14]. This puzzle also occurs in other spherical nuclei, such as Te and Pd [12]; therefore, herein, it is called the spherical nucleus puzzle. In this puzzle, the phonon excitation of the spherical shape is questioned and refuted. As Heyde and Wood stated, “deformation has become a major observed excitation mode, making rigid spherical nuclei rather the exception”, “a shift in perspective is required: sphericity is a special case of deformation” [11]. In the SU3-IBM, with the aid of SU(3) higher-order interactions, a similar spherical-like γ-soft spectra was found, and the spherical shape was replaced by a special quadrupole deformation [1].Recently, another unexpected phenomenon, called the B(E2) anomaly, was also observed [15−18]. In neutron-deficient nuclei 168Os, 166W, 172Pt, 170Os, a very small
$ B_{4/2}=B(E2; 4_{1}^{+}\rightarrow 2_{1}^{+})/B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ was found, which is much smaller than 1.0 (a single particle feature). In these nuclei, the energy ratio$ E_{4/2}=E_{4_{1}^{+}}/E_{2_{1}^{+}} $ between the$ 4_{1}^{+} $ and$ 2_{1}^{+} $ states is larger than 2.0. Therefore, they exhibit a collective excitation. Generally, a small$ B_{4/2} $ value should not appear in the collective behaviors. The B(E2) anomaly also rejects conventional theoretical explanations, including the interacting boson model (IBM-2) calculations based on the SkM$ ^{*} $ energy-density functional and symmetry-conserving configuration mixing (SCCM) calculations [15−18]. In the SU3-IBM, this anomaly can be also explained [2, 3]. Note that this is still the only explanation, and the B(E2) anomaly is also related to γ-softness [2].A successful explanation of these two abnormal phenomena would make the new theory of SU3-IBM very attractive, and further exploration of the applications of the theory has become very valuable, particularly on various γ-soft-like phenomena in nuclear spectra. We must emphasize that these two anomalous phenomena cannot be explained by the interacting boson model with the
${O}(6) \;\; \gamma$ -softness [6]. Recent studies on the prolate-oblate asymmetric shape phase transition have revealed that the key ingredient of the new model SU3-IBM is describing the oblate shape with the SU(3) third-order interaction [4]. γ-softness results from the competition between the prolate and oblate shapes. Thus, in the SU3-IBM, the new γ-softness is an emergent phenomenon, which differs from the usual O(6) description [19].The IBM provides an elegant approach to describing the low-lying collective excited behaviors in nuclear structures [19, 20]. In the simplest IBM-1, the basic building constituents are the s and d bosons with angular momentums of
$ l=0 $ and$ l=2 $ , respectively, and the collective states of a nucleus can be spanned by SU(6) algebra. Up to two-body interactions, the consistent-Q (CQ) Hamiltonian adopted in this model is [21, 22]$ \hat{H}_{1}=c\left[(1-\eta) \hat{n}_{d}-\frac{\eta}{N}\hat{Q}_{\chi}\cdot \hat{Q}_{\chi}\right]. $

(1) Here,
$ \hat{n}_{d}=d^{\dagger}\cdot \tilde{d} $ is the d-boson number operator,$\hat{Q}_{ \chi}= [d^{\dagger}\times\tilde{s}+s^{\dagger}\times \tilde{d}]^{(2)}+\chi[d^{\dagger}\times \tilde{d}]^{(2)}$ is the generalized quadrupole operator, N is the total boson number, c is a scale parameter, and$0\leqslant \eta \leqslant 1,\; -{\sqrt{7}}/{2}\leqslant \chi \leqslant {\sqrt{7}}/{2}$ are parameters that enable spanning a full range of different nuclear spectra. Although the formalism is simple, it can describe the spherical ($ \eta=0 $ , the$U(5)$ limit), prolate ($ \eta=1 $ ,$\chi=-{\sqrt{7}}/{2}$ , the$ {{S U}}(3) $ limit), oblate ($ \eta=1 $ ,$\chi={\sqrt{7}}/{2}$ , the$\overline{ {S U(3)}}$ case), and γ-unstable ($ \eta=1 $ ,$ \chi=0 $ , the${O}(6)$ limit) nuclei. This Hamiltonian is extensively used in fitting realistic nuclear spectra and discussing the shape phase transitions between different shapes [20−24].More than a decade ago, one of the authors (L. Fortunato) and his collaborators generalized the simple formalism (1), and a cubic-Q interaction was introduced as follows [25]:
$ \hat{H}_{2}=c\left[(1-\eta) \hat{n}_{d}-\frac{\eta}{N}(\hat{Q}_{\chi}\cdot \hat{Q}_{\chi}+ \frac{\kappa_{3}}{N}[\hat{Q}_{\chi}\times \hat{Q}_{\chi}\times \hat{Q}_{\chi}]^{(0)})\right], $

(2) where
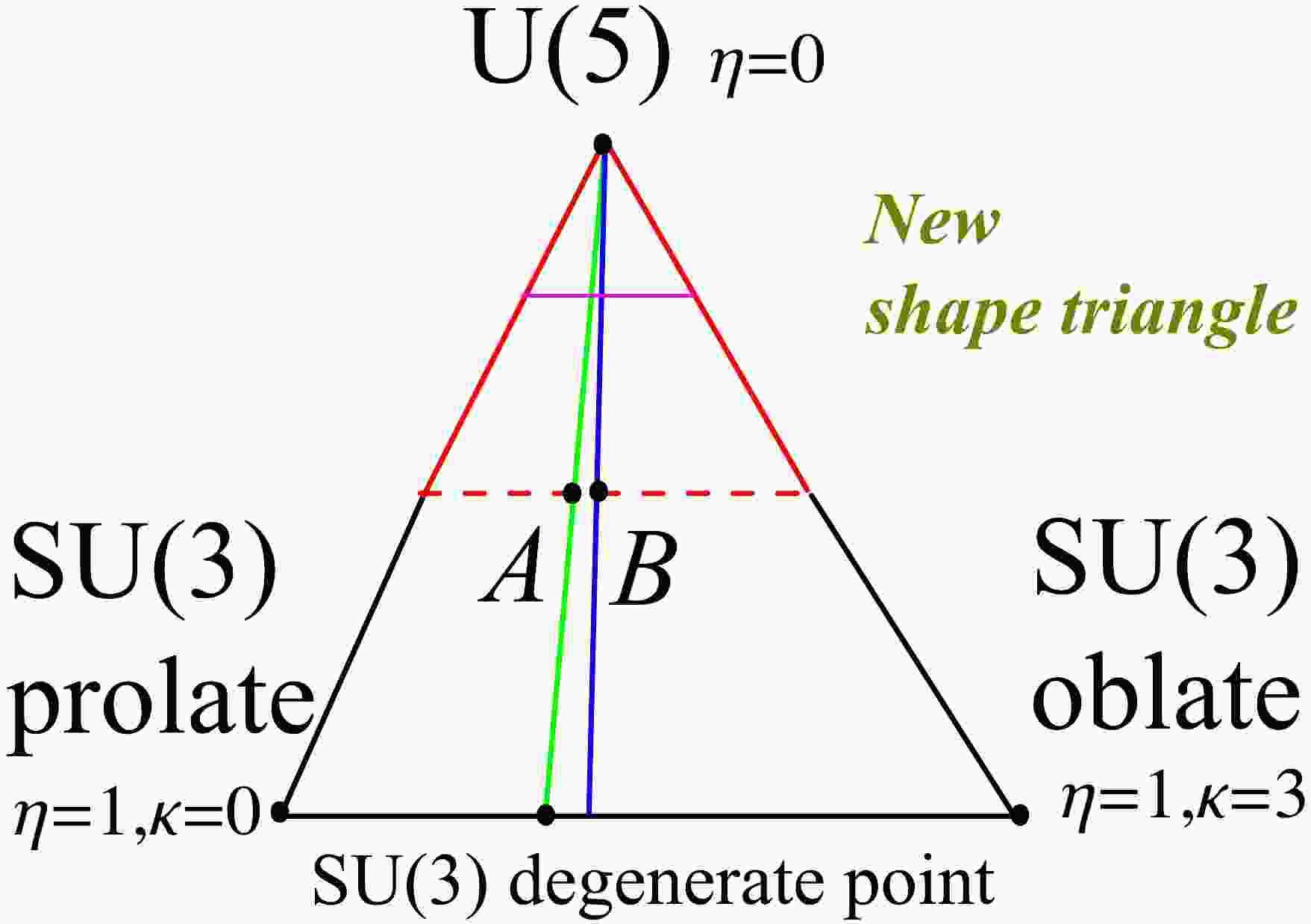
$ \kappa_{3} $ is the coefficient of the cubic term. In the${S U}(3)$ limit, when$\chi=-{\sqrt{7}}/{2}$ , the cubic interaction can describe an oblate shape (${S U}(3)$ oblate), which differs from the previous$\overline{ {S U(3)}}$ oblate shape in Hamiltonian (1). This indicates that the previous description of the oblate shape with$\overline{ {S U(3)}}$ symmetry can be replaced by the${S U}(3)$ symmetry, and a new evolutional path from the prolate shape to the oblate shape can be established within only the${S U}(3)$ limit (bottom black line in Fig. 1). Thus, an analytically solvable prolate-oblate shape phase transitional description within the${S U}(3)$ limit can be provided [26], which offers a rare example for finite-N first-order quantum shape transition. The phase transitional point is also a degenerate point [26], which implies a hidden symmetry [1]. This degenerate point is called the SU(3) degenerate point (black point in the bottom black line in Fig. 1). This hidden symmetry is responsible for the entire new progress in [1−6]. Moreover, this extended Hamiltonian$ \hat{H}_{2} $ contains is only a tiny region of rigid triaxiality in the large-N limit at$\chi=-{\sqrt{7}}/{2}$ when the parameter changes from the$ U(5) $ limit to the$ {{S U}}(3) $ degenerate point (green line in Fig. 1).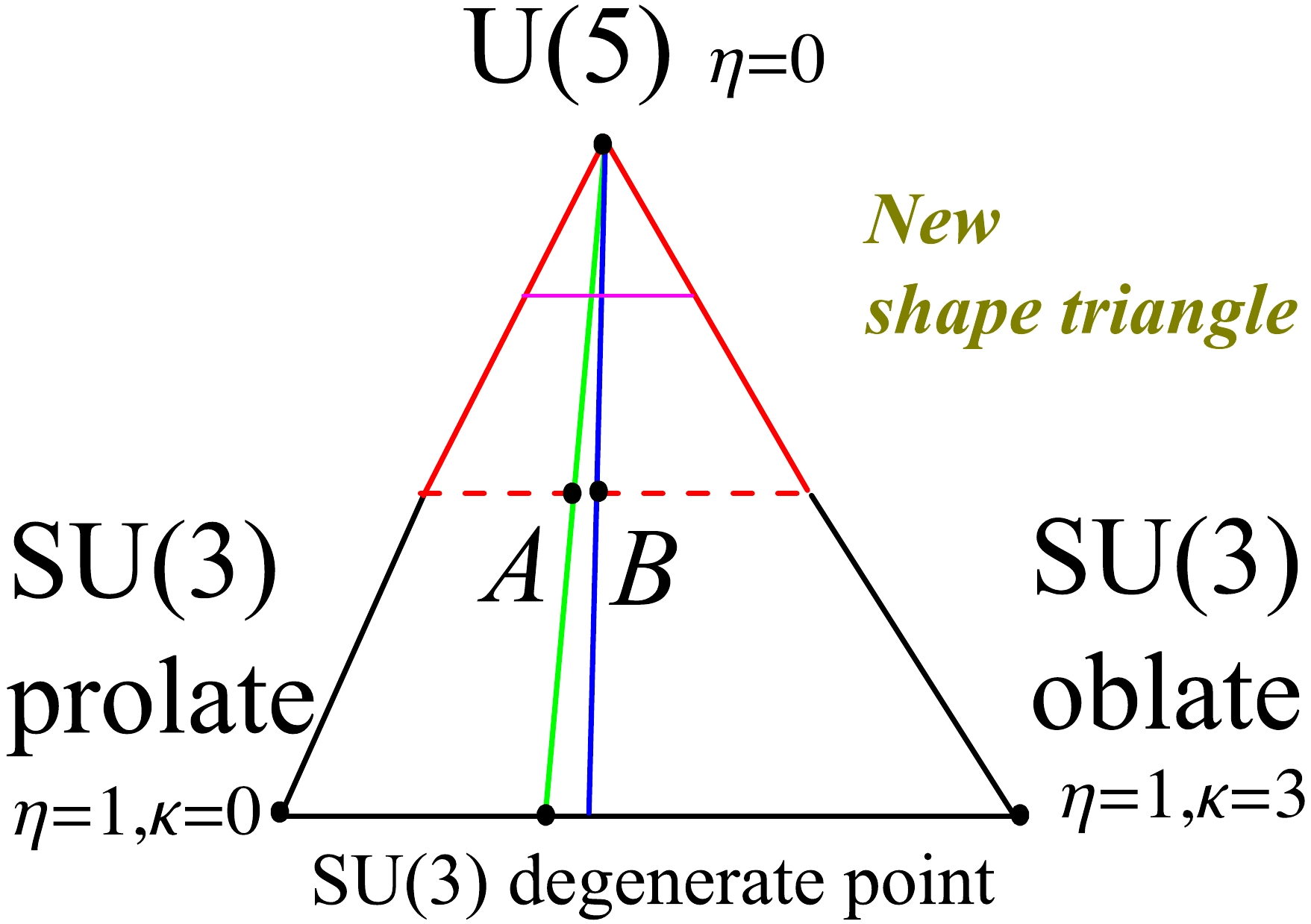
Figure 1. (color online) New shape triangle: the top point of the triangle presents the
$ U(5) $ limit, which is spherical. The two bottom points and black line between them are all within the$ {{S U}}(3) $ limit.The left bottom point presents the$ {{S U}}(3) $ prolate shape, and the right one presents the$ {{S U}}(3) $ oblate shape. The middle point of the green line is point A, which is discussed in [1]. The middle point of the blue line is point B, which is discussed in this paper.These new results presented by Refs. [25, 26] encourage us to explore the existing experimental phenomena from a new perspective. Some new and unexpected results have emerged recently. A new shape triangle can be plotted (see Fig. 1), which is similar to the Casten triangle related to the Hamiltonian (1) [27]. In the new SU3-IBM theory [1], a new γ-soft-like triaxial rotation is found, which differs from the
${{O}}(6) \;\; \gamma$ -unrelated rotational mode in Hamiltonian (1). The shape transitional behaviors from the$ U(5) $ limit to the$ {{S U}}(3) $ degenerate point was numerically explored (green line in Fig. 1). Within the parameter region of the green line in Fig. 1, we find an unexpected result in that an accidental degeneracy of the corresponding energy levels occurs between the ground and quasi-γ bands such that they form an exactly degenerate multiplet (top graph in Fig. 2). The ensuing discussion will clarify that while this degenerate multiplet corresponds to that found in the$SO(5)$ symmetry with quantum number$ \tau=2 $ , the next one ($ \tau=3 $ ) is not exactly degenerate. This characteristic is often observed in actual nuclear spectra. The key observation is that, spherical-like γ-soft triaxial rotational spectra actually exist (bottom graph in Fig. 2), which may be the candidate for solving the spherical nucleus puzzle [7, 11, 12]. This spherical-like spectra was not shown in [1].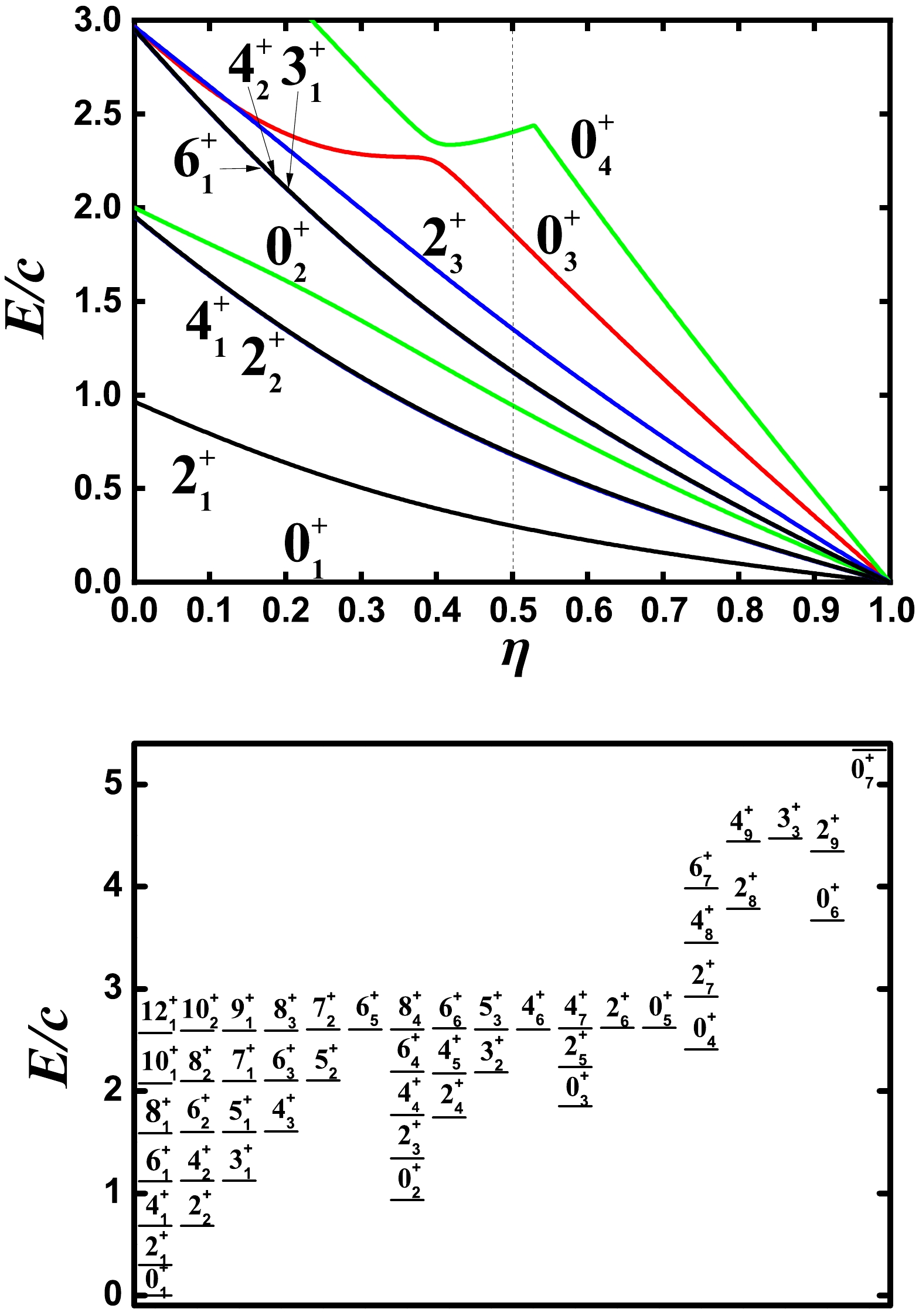
Figure 2. (color online) Top: Partial low-lying level evolution along the green line in Fig. 1 for
$ N=6 $ . Bottom: Spherical-like spectra of point A for$ N=6 $ .Historically, higher-order interactions in IBM-1 were introduced to describe γ-rigid triaxial deformation and interactions
$ [d^{\dagger}d^{\dagger}d^{\dagger}]^{(L)}\cdot[\tilde{d}\tilde{d}\tilde{d}]^{(L)} $ can play an essential role in the triaxiality of the ground state [28, 29]. An important progress related with our research is investigating$ {{S U}}(3) $ symmetry-conserving higher-order interactions [30]. Subsequently, within the$ {{S U}}(3) $ limit, an algebraic realization of the rigid asymmetric rotor was established [31, 32]. Recently, this realization has been used to explain the$ B(E2) $ anomaly [3].$ {{S U}}(3) $ third-order and fourth-order interactions were also discussed in Refs. [33−36]. Higher-order terms are also important in partial dynamical symmetry [37]. The higher-order interaction$ (\hat{Q}_{0}\times\hat{Q}_{0}\times\hat{Q}_{0})^{(0)} $ can present a rotational spectrum [38], where$ \hat{Q}_{0} $ is the quadrupole operator in the${O}(6)$ limit. This result was further studied by [39, 40]. However the O(6) symmetry was questioned in [6]. In these series of new developments [1−6, 25, 26, 31, 32],$ {{S U}}(3) $ higher-order interactions begin to have an extremely important role, albeit at a phenomenological level. These higher-order interactions have already been shown to be relevant to some realistic anomalies in nuclear structure [1−3]. Therefore, introducing these terms is of practical significance.The γ-soft shape, where the geometric Hamiltonian is not dependent on the γ variable, was first described in Ref. [41]. In the IBM, the γ-soft case can be described using the
${O}(6)$ limit [19, 42], and the nucleus of 196Pt was the first candidate for the${O}(6)$ spectra. However, some debate about it remains [43, 44]. In the IBM-2 [20], the triaxial shape can be described even with up to two-body interactions [45−47]. Three-body interactions$ [d^{\dagger}d^{\dagger}d^{\dagger}]^{(L)}\cdot [\tilde{d}\tilde{d}\tilde{d}]^{(L)} $ are also used in the IBM-2 to investigate γ triaxiality [48]. In the sdg-IBM,$ l=4 $ g bosons can be introduced and hexadecapole deformation can be discussed [49]. Except for the IBM, triaxial shapes are also investigated by many existing nuclear models [7, 21, 50−56].Although 196Pt appears to adapt to the description in terms of
${O}(6)$ symmetry, some noticeable deviations still exist and cannot be described at a satisfactory level in the IBM. The first limitation is that it has a large electric quadrupole moment [43],$ Q_{2_{1}^{+}} $ =0.62(8), pointing towards the oblate side. The second is that the staggering feature of γ band breaks${O}(5)$ symmetry, which appears to be intermediate between the γ-soft and γ-rigid. The third is the positions of the$ 0_{2}^{+} $ ,$ 0_{3}^{+} $ ,$ 0_{4}^{+} $ states, which can not be reproduced well [57].Recently, two important results in the SU3-IBM have also been found [4, 5]. In [4], the SU(3)-IBM was used to describe the prolate-oblate shape phase transition with an asymmetric manner, which can adequately explain the shape transitions from 180Hf to 200Hg including the nucleus 196Pt. The transitional region is selected along the dashed red line in Fig. 1, which passes through the middle point A of the transitonal region from the U(5) limit to the SU(3) degenerate point. In this shape phase transition, another special point that exhibits accidental degeneracy features can be located near the middle of the degenerate line (point B in Fig. 1,) and it can be used to describe the properties of 196Pt [4]. In [5], a shape transitional behavior similar to that from the
$ U(5) $ limit to the${O}(6)$ limit in IBM was observed by introducing the$ {{S U}}(3) $ fourth-order interaction, which can describe the$E(5)$ -like γ-softness in 82Kr.Following the concepts of the previous studies, further exploration of the applications of the SU3-IBM is necessary. 196Pt is the focus. The three apparent deficiencies discussed above can be adequately overcome simultaneously. This nucleus is frequently considered a typical example with
${O}(5)$ symmetry in Hamiltonian (1). We have found that the new model can provide a more reasonable description, and our work provides a new understanding for γ-softness in 196Pt and other similar nuclei, which is related with the SU(3) symmetry. Thus, these results in the SU3-IBM ([1−6] and this paper) together confirm the validity of the new concept.This is the first paper in which the nucleus 196Pt is discussed in terms of the SU(3) higher order interactions. In the SU(3) limit, three interactions (the SU(3) second-order Casimir operator
$ \hat{C}_{2}[{S U(3)}] $ , SU(3) third-order Casimir operator$ \hat{C}_{3}[{S U(3)}] $ , and square of the second-order Casimir operator$ \hat{C}_{2}^{2}[{S U(3)}] $ ) can determine the quadrupole shape of the ground state and the energies of the$ 0^{+} $ states [5]. In this paper, the three operators are first investigated to fit the lowest few$ 0^{+} $ states in 196Pt. Other three operators ($ [\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ ,$ [(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ , and$ \hat{L}^{2} $ ) can describe the triaxial rotational spectra [31, 32], which will be discussed in the series of subsequent papers. -
In the SU3-IBM, the d boson number operator
$ \hat{n}_{d} $ must be included, which can describe a spherical shape. This is vital to the pairing interaction between the valence nucleons. The other interacting terms are all$ {{S U}}(3) $ conserving invariants. The traditional second-order interaction$ -\hat{C}_{2}[{S U(3)}] $ can describe the prolate shape. Ref. [25] indicated that the third-order Casimir operator$ \hat{C}_{3}[{S U(3)}] $ can describe the oblate shape. Other higher-order interactions should be considered in some peculiar phenomena, such as$ B(E2) $ anomaly and some unusual experimental data that cannot be described by previous theories [2, 3]. In [5], the square of the second-order Casimir operator$ \hat{C}_{2}^{2}[{S U(3)}] $ was found to be vital to the γ-softness of the realistic nuclei. In this paper, the third-order invariant operator and the square of the second-order invariant operator are introduced into the interactions, similar to Ref. [5] (the fourth-order interaction is only a supplementary term here). Although this is a simple formalism in the SU3-IBM, it reveals many new interesting phenomena. Thus, the Hamiltonian discussed in this paper is$ \begin{aligned}[b] \hat{H} = & c\left[(1-\eta)\hat{n}_{d}+\eta\left(-\frac{\hat{C}_{2}[ {S U(3)}]}{2N}\right.\right. \\ & \left.\left.+\kappa \frac{\hat{C}_{3}[ {S U(3)}]}{2N^{2}}+\xi\frac{\hat{C}_{2}^{2}[ {S U(3)}]}{2N^{3}} \right)\right], \end{aligned} $

(3) where
$ 0\leqslant \eta \leqslant 1 $ , c is a global energy scale parameter, N is the boson number, κ is the coefficient of the cubic term,$ \kappa=\dfrac{9\kappa_{_{3}}}{2\sqrt{35}} $ , ξ is the coefficient of the fourth-order interaction, and$ \hat{C}_{2}[{S U(3)}] $ and$ \hat{C}_{3}[{S U(3)}] $ are the second-order and third-order$ {{S U}}(3) $ Casimir operators, respectively. If the fourth-order term is not considered, that is$ \xi=0.0 $ , the Hamiltonian (3) can be described by the new shape triangle in Fig. 1.Figure 1 requires some explanations. As introduced earlier, the top point of the new triangle in Fig. 1 is the U(5) limit (
$ \eta=0.0 $ ), which results from the pairing interaction between nucleons and can introduce the spherical shape and phonon excitation. The spherical nucleus puzzle implies that this limit cannot exist alone. If$ \eta=1.0 $ , it is the SU(3) limit and corresponds to the two bottom points and the black line between them. The left bottom point presents the SU(3) prolate shape ($\eta=1.0, \kappa=0.0$ ), and the right one presents the SU(3) oblate shape ($\eta=1.0,\;\kappa=3.0$ ). Thus, the bottom black line presents the shape transition from the prolate to oblate shape [3]. These quadrupole shapes can be described by the SU(3) irrep$ (\lambda,\mu) $ . For a certain boson number N, the prolate shape is (2N, 0) while the oblate one is (0, N). Thus the spectra of the prolate and oblate shapes are not the same, which is different from the old IBM with$ \overline{ {S U(3)}} $ symmetry.The shape critical point between the prolate shape and the oblate shape is the SU(3) degenerate point [1, 26], which is denoted by the black point in the bottom black line. On the left side of this degenerate point, the shape is prolate, whereas, at the right side, it is oblate. This degenerate point inspires the SU3-IBM. The green line between the U(5) limit to the SU(3) degenerate point is the degenerate line where the
$ 4_{1}^{+} $ state and the$ 2_{2}^{+} $ state are degenerate (top graph ofFig. 2). The green line is not straight but curved. However, the straight line is a suitable approximation if N is small [4]. The top part of the purple line (near$ \eta=0.2 $ ) is spherical, and the bottom part ($0.2 < \eta \leqslant 1.0$ ) presents the deformations. The middle point A of the green line is in the deformation region. We found that this point A has the spherical-like spectra (bottom graph of Fig. 2). The dashed red line passes through point A, which was discussed in [4] to investigate the asymmetric shape phase transition from the prolate to oblate shape in the Hf-Hg nuclei region. The study found that another accidental degenerate point B exists along the dashed red line between the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states (Fig. 3). Interestingly, 196Pt was observed to be located at this point B. The blue line begins from the U(5) limit and passes through point B, which is the transitional region discussed in this paper.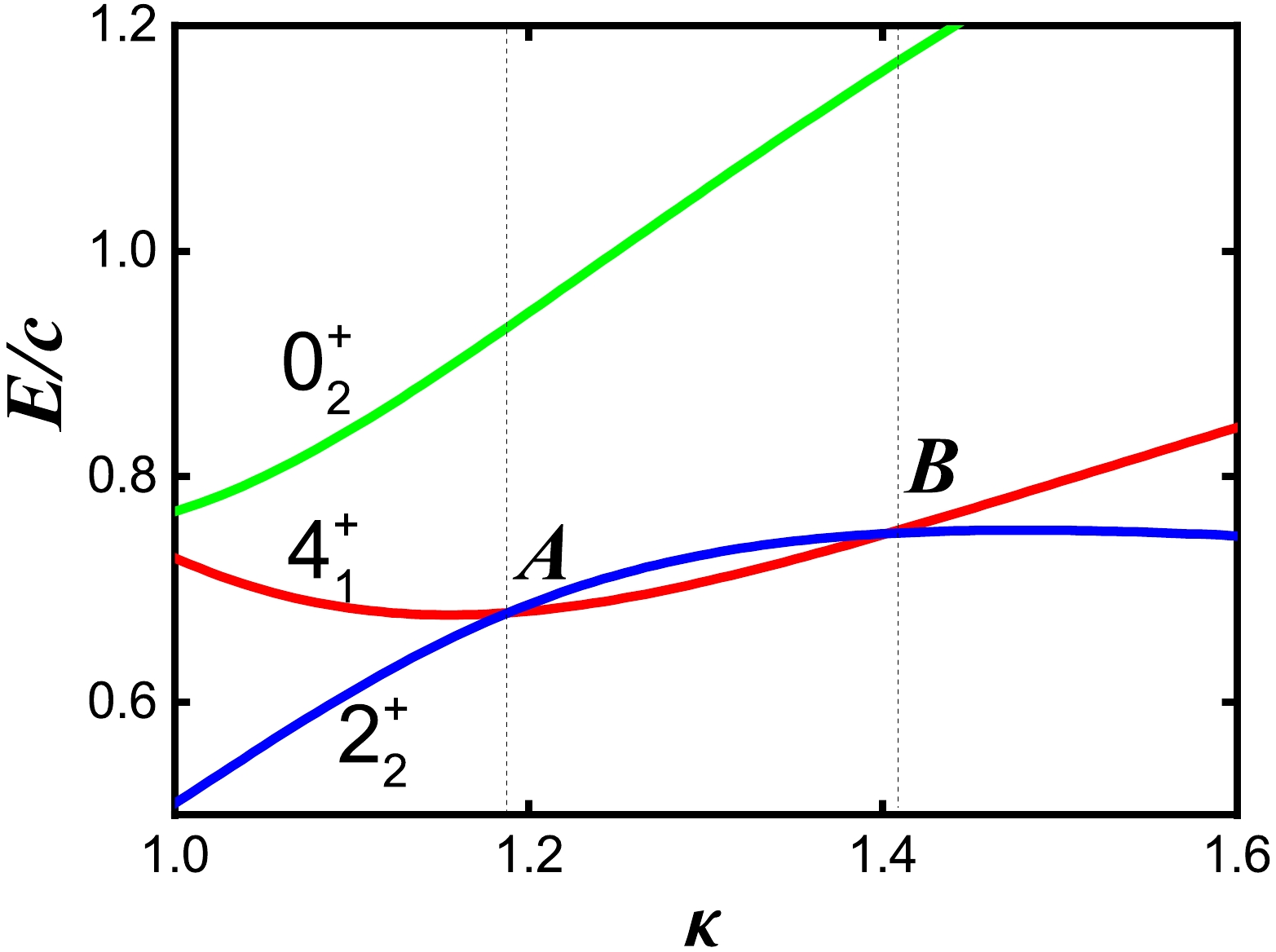
Figure 3. (color online) Level evolution of the
$ 4_{1}^{+} $ ,$ 2_{2}^{+} $ and$ 0_{2}^{+} $ states for the parameter κ from 1.0 to 1.6 when$ \eta=0.5 $ ,$ \xi=0 $ and$ N=6 $ . Two crossing points A and B, where accidental degeneracy occurs, can be observed.In the
$ {{S U}}(3) $ limit, the two Casimir operators can be related with the quadrupole second or third-order interactions as follows [26, 36]:$ \hat{C}_{2}[ {S U(3)}]=2\hat{Q}\cdot \hat{Q}+\frac{3}{4} \hat{L}\cdot \hat{L}, $

(4) $ \hat{C}_{3}[ {S U(3)}]=-\frac{4\sqrt{35}}{9}[\hat{Q}\times \hat{Q} \times \hat{Q}]^{(0)}-\frac{\sqrt{15}}{2}[\hat{L}\times \hat{Q} \times \hat{L}]^{(0)}, $

(5) where
$ \hat{Q}=[d^{\dagger}\times\tilde{s}+s^{\dagger}\times \tilde{d}]^{(2)}-\dfrac{\sqrt{7}}{2}[d^{\dagger}\times \tilde{d}]^{(2)} $ is the SU(3) quadrupole operator, and$ \hat{L}=\sqrt{10}[d^{\dagger}\times \tilde{d}]^{(1)} $ is the angular momentum operator. For a given$ {{S U}}(3) $ irrep$ (\lambda,\mu) $ , the eigenvalues of the two Casimir operators under the group chain${{U(6)}}\supset {S U(3)} \supset {{O(3)}}$ are given as$ \langle \hat{C}_{2}[ {S U(3)}]\rangle=\lambda^{2}+\mu^{2}+\lambda \mu+3\lambda+3\mu, $

(6) $ \langle \hat{C}_{3}[ {S U(3)}]\rangle=\frac{1}{9}(\lambda-\mu)(2\lambda+\mu+3 ) (\lambda+2\mu+3 ). $

(7) If
$ \kappa=\dfrac{3N}{2N+3} $ , the second term in Hamiltonian (3) describes the$ {{S U}}(3) $ degenerate point ($ \xi=0 $ ). Note that the location of the$ {{S U}}(3) $ degenerate point along the variable κ is related to the boson number N [4]. For 196Pt,$ N=6 $ , it is found at$ \kappa =1.2 $ . In the large-N limit,$ \kappa \rightarrow 1.5 $ . At this degenerate point, the$ {{S U}}(3) $ irreps satisfying the condition$ \lambda+2\mu=2N $ are all degenerate.The Hamiltonian (3) is diagonalized using our SU(3) basis diagonalization Fortran code [22] with the
$ U(6)\supset S U(3) \supset S O(3) $ basis spanned by$ { | N(\lambda,\mu)\chi L \rangle} $ , where χ is the branching multiplicity occurring in the reduction of$ S U(3)\downarrow S O(3) $ . The basis vectors are orthonormal; therefore, the eigenstates can be expressed as$ |N,L_{\zeta};\eta,\kappa,\xi\rangle =\sum\limits_{(\lambda,\mu)\chi}C^{L_{\zeta}}_{(\lambda,\mu)\chi}(\eta,\kappa,\xi)| N(\lambda,\mu)\chi L \rangle, $

(8) where ζ is an additional quantum number distinguishing different eigenstates with the same angular momentum L, and
$ C^{L_{\zeta}}_{(\lambda,\mu)\chi}(\eta,\kappa,\xi) $ is the corresponding expansion coefficient. We plan to publish this Fortran code in a forthcoming paper. -
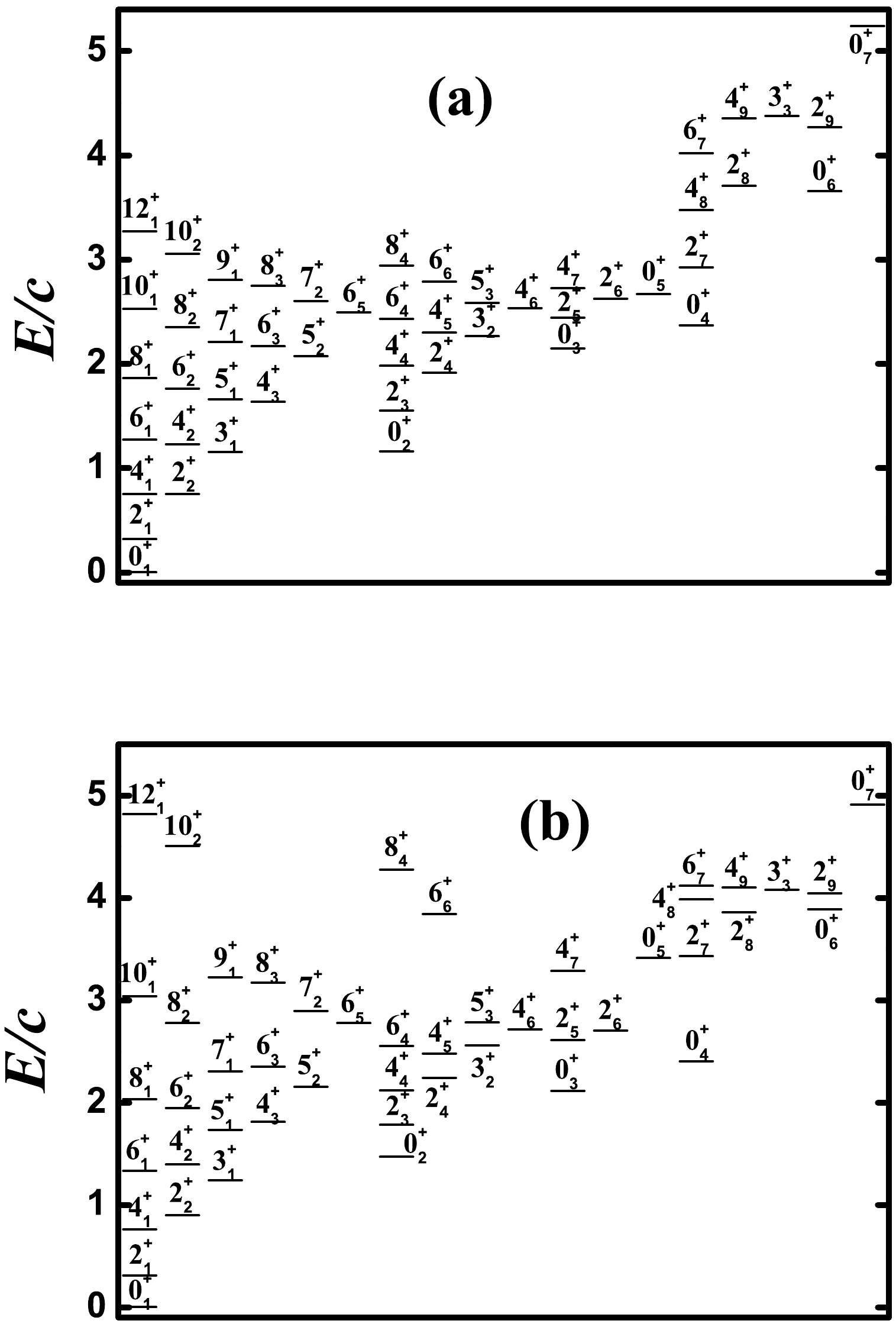
The top graph of Fig. 2 presents the partial low-lying level evolutions from the
$ U(5) $ limit to the$ {{S U}}(3) $ degenerate point for$ N=6 $ as a function of η. The choice of the boson number$ N=6 $ correponds to 196Pt. (In the previous paper [1],$ N=7 $ was discussed for 110Cd.) We can clearly observe that the four lowest$ 0^{+} $ states are all degenerate if$ \eta=1.0 $ . The key finding is that the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states, as well as the triplet states$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ and,$ 3_{1}^{+} $ , are degenerate. This degeneracy can hold for some higher levels. However, the reason for this degeneracy is still unknown. This unexpected γ-softness was discussed in [1].The SU(3) degenerate point is found at
$ \kappa=1.2 $ . A further exploration around this degenerate point is useful for understanding the new γ-softness. Figure 3 plots the level evolution of the$ 4_{1}^{+} $ ,$ 2_{2}^{+} $ , and$ 0_{2}^{+} $ states for the parameter κ from 1.0 to 1.6 when$ \eta=0.5 $ ,$ \xi=0 $ , and$ N=6 $ . Two crossing points occur between the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states at$ \kappa_{A}=1.188 $ and$ \kappa_{B}=1.404 $ . The position relationships of these three states are very important for understanding γ-softness in realistic nuclei. The left one is the point A, and the right point is point B, which is the special point discussed in this paper. The location of the point B is$ \kappa_{B}=1.404 $ . Point A is biased toward the prolate side and point B toward the oblate side. In the γ-soft-like region between the two points, point B is closest to the oblate shape. 196Pt is a γ-soft nucleus with large positive quadruple moment; therefore, it is natural to investigate whether the spectrum at point B can be used to describe this nucleus. Note that the value of$ \kappa_{A}=1.188 $ is slightly smaller than that of the$ {{S U}}(3) $ degenerate point, 1.2; thus, the real degenerate line between the$ U(5) $ limit and the$ {{S U}}(3) $ degenerate point is not the directly connected green line in Fig. 1 [25], which was also discussed in [4]. A sudden shape change occurs through the$ {{S U}}(3) $ degenerate point from the prolate to oblate shape [26]. However, in the large-N limit [25], point A is the critical point between the prolate and γ-rigid triaxial shapes, whereas point B is the critical point between the γ-rigid triaxial and oblate shapes. Thus, the positions of these points differ from each other [4]. However, for a small N, this connected line is a suitable approximation [4]. In Fig. 1, the blue line passes through point B. Note that, for any$ N\geqslant 4 $ , this special point B exists.In [1], the normal states in Cd isotopes were proposed to be a new collective excited mode. The key observation was that the
$ 0_{3}^{+} $ state does not exist at the three phonon level, but a$ 0_{2}^{+} $ state exists at the two phonon level. Thus, the$ 0_{3}^{+} $ state is repelled to a higher level, and the energy ratio betwen the$ 0_{3}^{+} $ and$ 0_{2}^{+} $ states is nearly 2.0. Although this large ratio is vital for the new spherical-like spectra, it is impractical for fitting 196Pt. For point B, this large ratio still exists (Fig. 4 at$ \xi=0.0 $ ). Ref. [5] found that the introduction of the fourth-order interaction$ \hat{C}_{2}^{2}[{S U(3)}] $ can reduce the energy difference between the$ 0_{2}^{+} $ and$ 0_{3}^{+} $ states, even to zero. Fig. 4 presents the level evolutions of$ 0_{2}^{+} $ and$ 0_{3}^{+} $ states when ξ increases from 0 to 0.3 for$ \eta=0.5 $ and$ \kappa=1.404 $ . Note that the fourth-order interaction is only a supplementary term here [4]; therefore, the value of ξ is small. The distance between the two states initially decreases and then increases. The minimum value is approximately$ \xi=0.144 $ , at which the energy ratio is 1.188, which is much smaller than 2.0.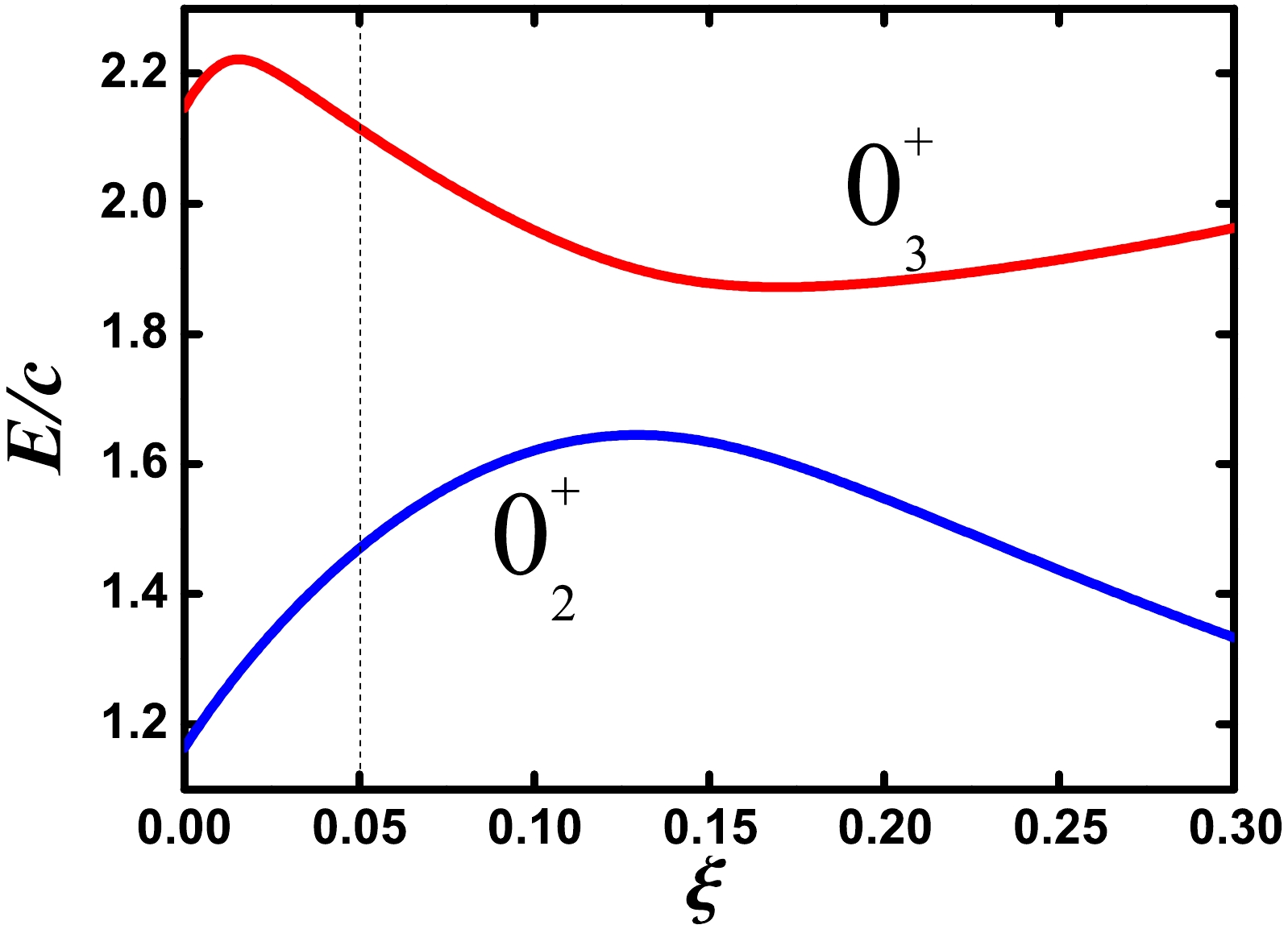
Figure 4. (color online) Level evolution of the
$ 0_{2}^{+} $ and$ 0_{3}^{+} $ states for the parameter ξ from 0 to 0.30 when$ \eta=0.5 $ ,$ \kappa=1.404 $ , and$ N=6 $ .Figure 5 (a) presents the partial low-lying level evolutions along the blue line via point B. The degeneracy between the ground band and γ-band is slightly broken, which can be also observed in Fig. 6 (a) for the energy spectra of point B. Compared with the top graph in Fig. 2, the levels of
$ 0_{2}^{+} $ and$ 2_{3}^{+} $ states rise slightly, and$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ ,$ 3_{1}^{+} $ , and$ 0_{2}^{+} $ are nearly degenerate. Thus, the low-lying part of the spectra is similar to that shown in the$O(6)$ limit [20]. For point B, the energies of$ 0_{2}^{+} $ and$ 0_{3}^{+} $ states are 1.1637c and 2.1472c in Fig. 5 (a). The ratio of the two states$ R'=E_{0_{3}^{+}}/E_{0_{2}^{+}}=1.845 $ is much larger than the experimental one (1.236). In this paper, for a better fitting of the quadruple moment, we select$ \xi=0.05 $ . Fig. 5 (b) presents the partial low-lying level evolutions when η varies from 0 to 1 for$ \kappa=1.404 $ and$ \xi=0.05 $ . The most significant change is that the positions of the$ 0_{2}^{+} $ state increases from 1.16c to 1.47c. The spectra of the position can be observed in Fig. 6 (b), which may be somewhat irregular. However, the low-lying part appears very similar to the spectra of the realistic γ-soft nucleus. For comparison, the bottom graph in Fig. 2 presents the spectra of the point A for$ N=6 $ , which was not shown in [1] and appears to be different from the two figures in Fig. 6. The low-lying part is very similar to the vibrational spectra of a rigid spherical nucleus. The key difference is that some bands ($ 0_{4}^{+} $ ,$ 2_{8}^{+} $ , and$ 0_{6}^{+} $ as bandheads) are significantly elevated. When moving from point A to B and adding a fourth-order term, the degeneracies are gradually broken, and the familiar γ-soft feature emerges, whereas the regularity of the spectra is weakened.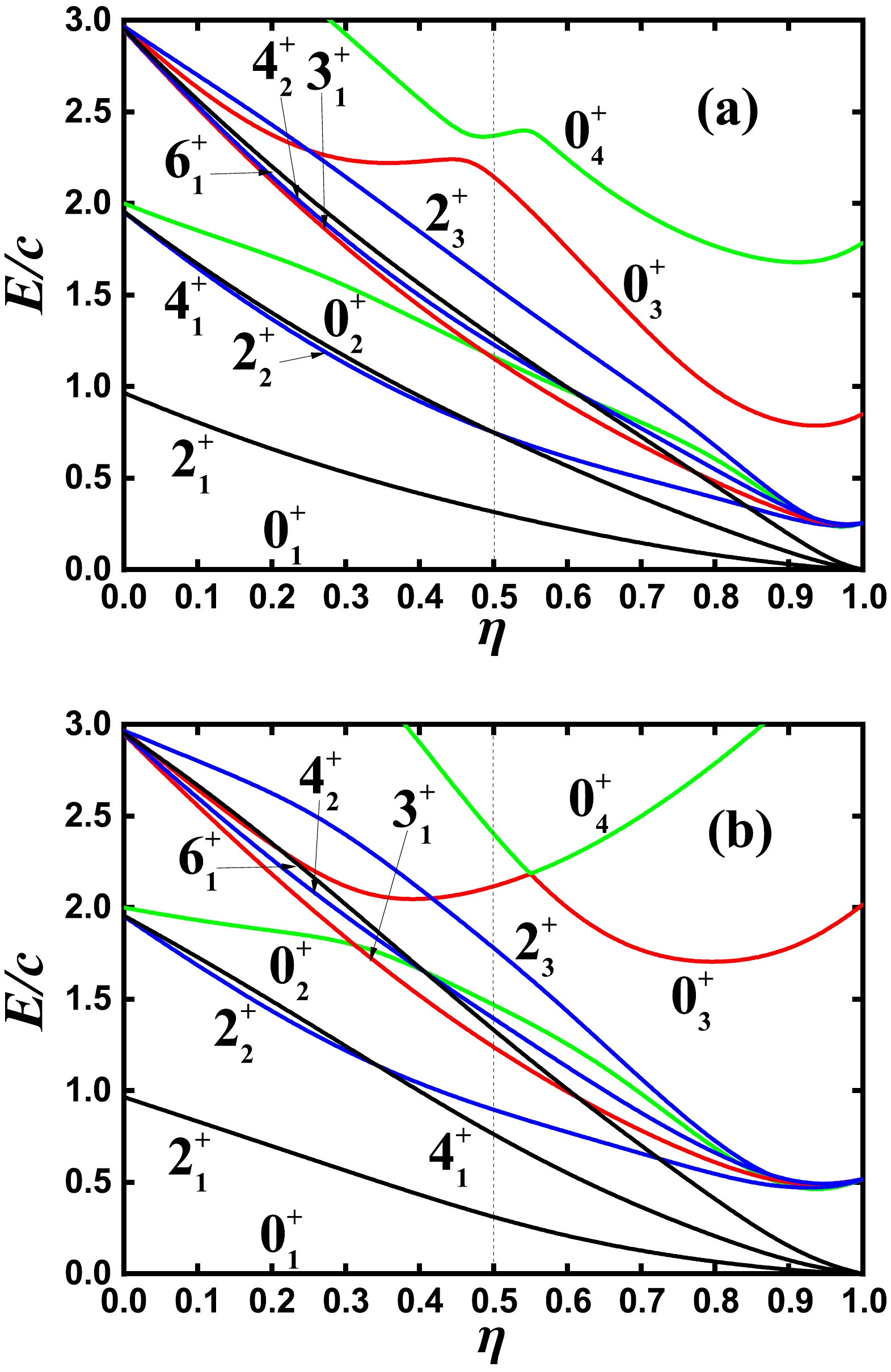
Figure 5. (color online) Partial low-lying level evolution along the blue line in Fig. 1 for
$ N=6 $ when (a)$ \xi=0 $ and (b)$ \xi=0.05 $ . -
The
$ B(E2) $ values are vital to understanding the collective behaviors. In the common experiences of nuclear structure studies, we often expect a definite relationship between the energy spectra and corresponding$ B(E2) $ values, particularly in the IBM. However, this relation may lead to the wrong conclusions. In the spherical nucleus puzzle [9, 11, 12], the energy spectra of the Cd isotopes are similar to those of the rigid spherical vibrations, but the$ B(E2) $ values have been experimentally found to violate the expectations. Thus, new perspectives on the shape evolution from the magic number nucleus to the deformation must be developed. In the$ B(E2) $ anomaly [15−18], this case becomes more apparent. From the level evolutions of the Pt-Os-W isotopes with neutron number, the energy spectra of 172Pt,$ ^{168,170} $ Os, and 166W appear normal, but their$ B(E2) $ values exceed expectations. Thus, collective behaviors cannot be determined solely by the energy spectra. Various nuclear spectroscopic methods are required [12].The
$ B(E2) $ values are also necessary for understanding γ -softness. Particularly when the new γ-softness is provided [1], distinguishing the different γ softness becomes increasingly important in the description of the realistic nuclei properties. The$ E2 $ operator is defined as$ \begin{array}{*{20}{l}} \hat{T}(E2)=e\hat{Q}, \end{array} $

(9) where e is the boson effective charge. The evolution of the
$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ ,$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ ,$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ ,$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ , and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ values are plotted along the blue line in Fig. 1 for$ N=6 $ . In Fig. 7 (a) the$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ value is nearly the same. For$ \eta=1.0 $ , it describes an oblate shape [26]. Thus, the$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ value is suppressed. With increasing η, the values of$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ decrease, whereas those of$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ increase. The trends are similar to those along the green line with degeneracy, and γ-softness can emerge. When the fourth-order interaction is introduced in Fig. 7 (b), at$ \eta=0.5 $ , the value of$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ can be reduced.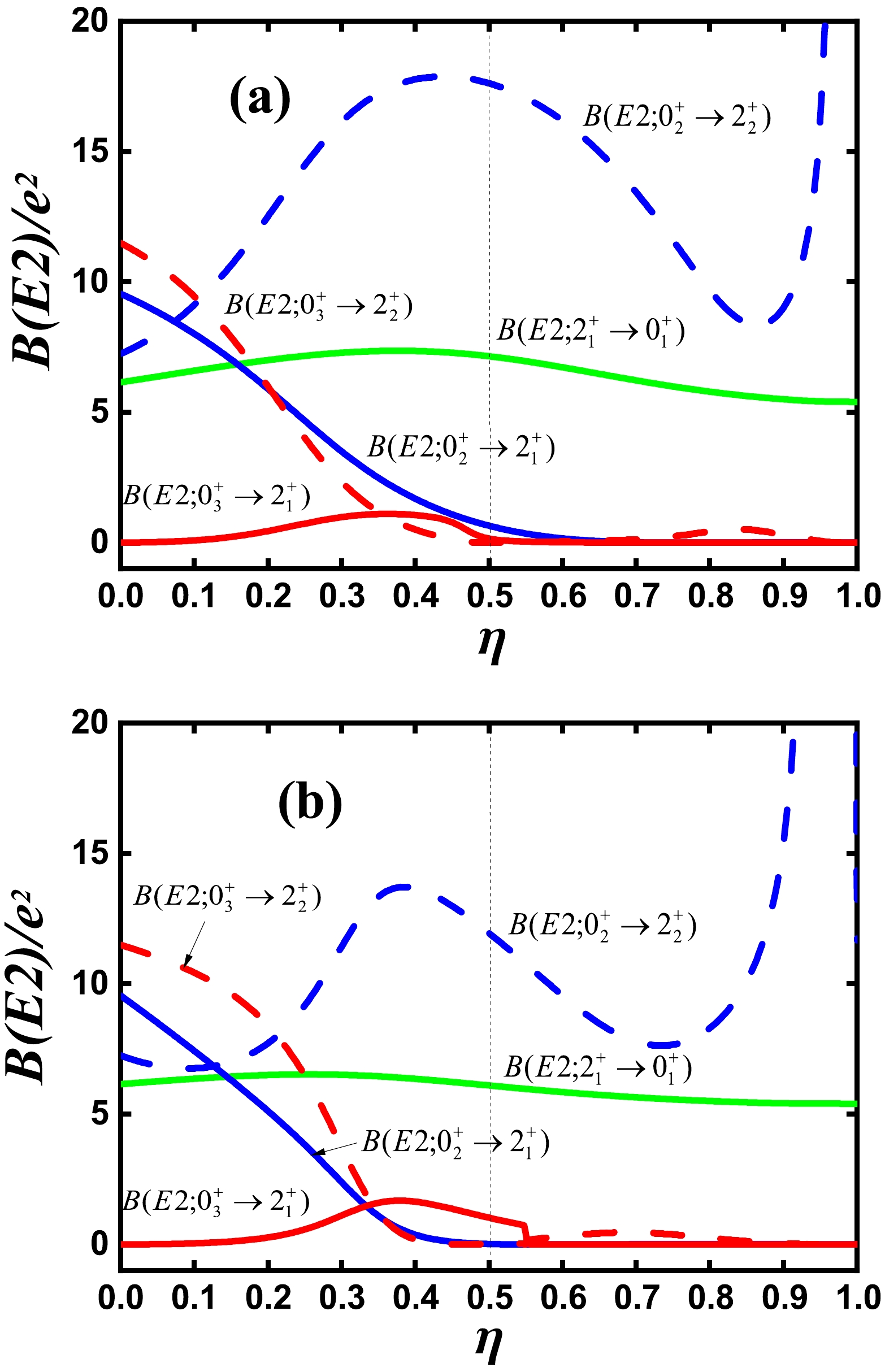
Figure 7. (color online) Evolution of
$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (solid green line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (solid blue line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (dashed blue line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (solid red line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (dashed red line) as functions of η when$ \kappa=1.404 $ : (a)$ \xi=0 $ and (b)$ \xi=0.05 $ for$ N=6 $ .Figure 8 shows the quadrupole moments of the
$ 2^{+}_{1} $ state for$ \xi=0 $ (solid blue line) and$ \xi=0.05 $ (solid red line). For the blue line, when$ \eta\geqslant 0.372 $ , the value becomes positive, which indicates an oblate deformation. The red line bends to the oblate side. Note that the$ E2 $ operator is suitable here. For the U(5) limit, the quadrupole operator is$ [d^{\dagger}\times \tilde{d}]^{(2)} $ , with which the quadrupole moment of the$ 2^{+}_{1} $ state in the U(5) limit is negative (not zero) [20]. If the quadrupole operator is taken as that of the O(6) limit, namely$ \hat{Q}_{0}=[d^{\dagger}\times\tilde{s}+s^{\dagger}\times \tilde{d}]^{(2)} $ , then the quadrupole moment of the$ 2^{+}_{1} $ state in the U(5) limit is only zero. Thus, if$\hat{Q}=[d^{\dagger}\times\tilde{s}+s^{\dagger}\times \tilde{d}]^{(2)}-{{7}}/{2}[d^{\dagger}\times \tilde{d}]^{(2)}$ is used, in the SU(3) limit, it is the$ \hat{Q} $ , whereas in the U(5) limit, it has the same role as$ [d^{\dagger}\times \tilde{d}]^{(2)} $ . This can describe the real evolution. In the actual fitting, the key is that the effective charge will be different.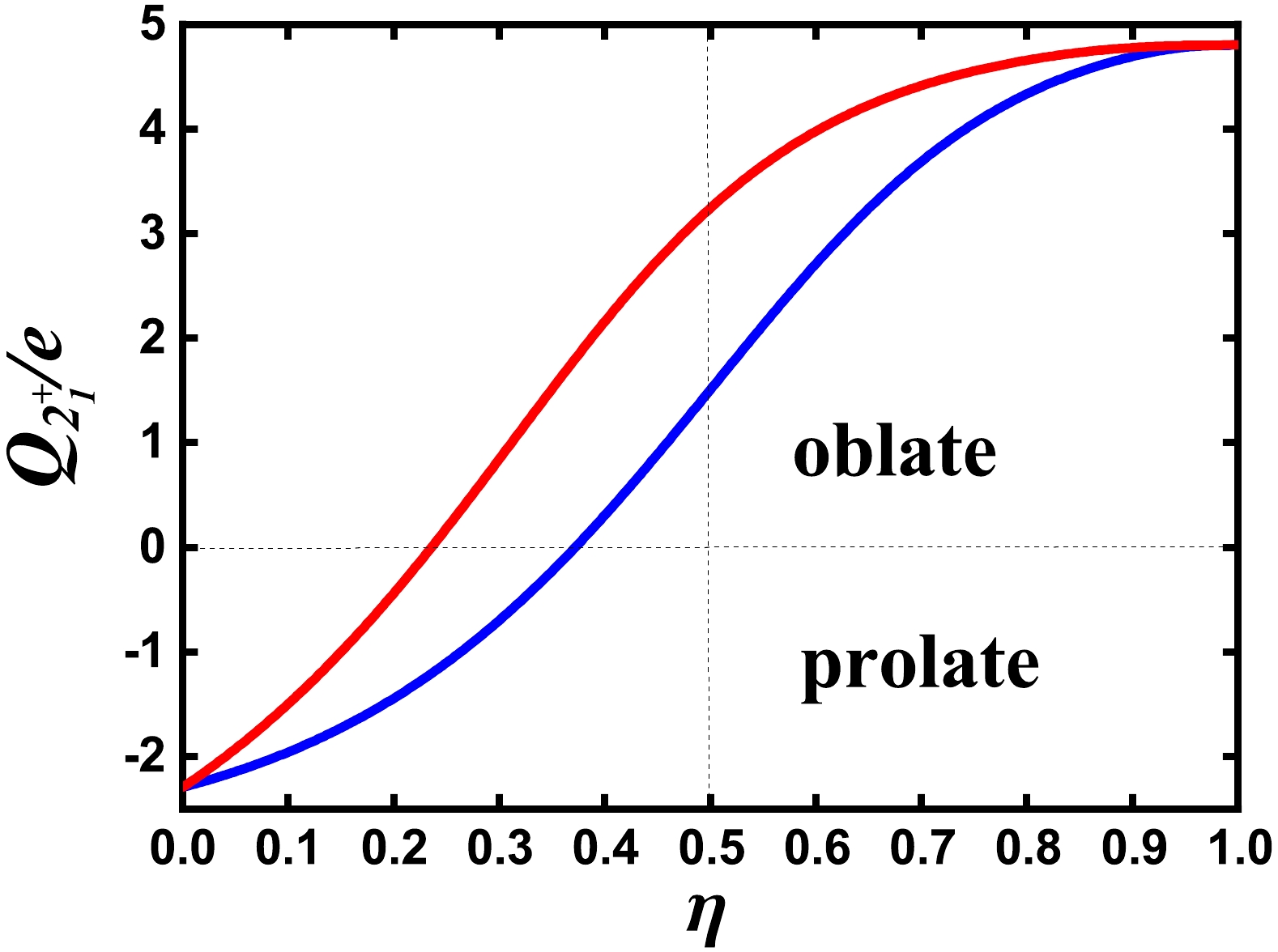
Figure 8. (color online) Evolution of the quadrupole moment of the
$ 2^{+}_{1} $ state along the blue line in Fig. 1 for$ N=6 $ when$ \xi=0 $ (solid blue line) and$ \xi=0.05 $ (solid red line). -
Without considering other higher-order interactions in the
$ {{S U}}(3) $ limit, the properties of point B or adding the fourth-order interaction are used to fit the structure of 196Pt. Although the precision must be improved, the fitting results appear to be excellent. For$ \xi=0 $ at point B, the overall energy parameter c in$ \hat{H} $ is 0.9753 MeV to make the energy value of the$ 0_{2}^{+} $ state equal to the experimental one. The$ L^{2} $ term is also added to fit the$ 2_{1}^{+} $ state, which is 0.00803 MeV. The theoretical spectra of point B shown in Fig. 9 (b) are compared with the experimental data shown in Fig. 9 (a). The theory and experiment correspond well qualitatively, and we can observe that the position relationships of each energy level are also consistent. The rotational-like γ-band in 196Pt is an interesting problem, and the theoretical spectra have similar structures.$ 0_{4}^{+} $ and$ 0_{5}^{+} $ states also fit well. The main limitation is that the$ 0_{3}^{+} $ ,$ 2_{5}^{+} $ , and$ 2_{6}^{+} $ states are slightly higher, that is, the energy difference between the$ 0_{3}^{+} $ and$ 0_{2}^{+} $ states is slightly larger than the experimental result. This is the typical characteristic of the new γ-soft-like rotational mode [1]. For$ \xi=0.05 $ , better fitting results can be obtained, where the characteristics of the γ band are consistent with the actual scenario, and the energies of the$ 0_{3}^{+} $ and$ 0_{4}^{+} $ states are also reduced. To reduce the energies of the higher-levels, Pan et al. presented a new method to provide an excellent fitting result for 194Pt [58], which may be used to improve the fitting precision in the SU3-IBM.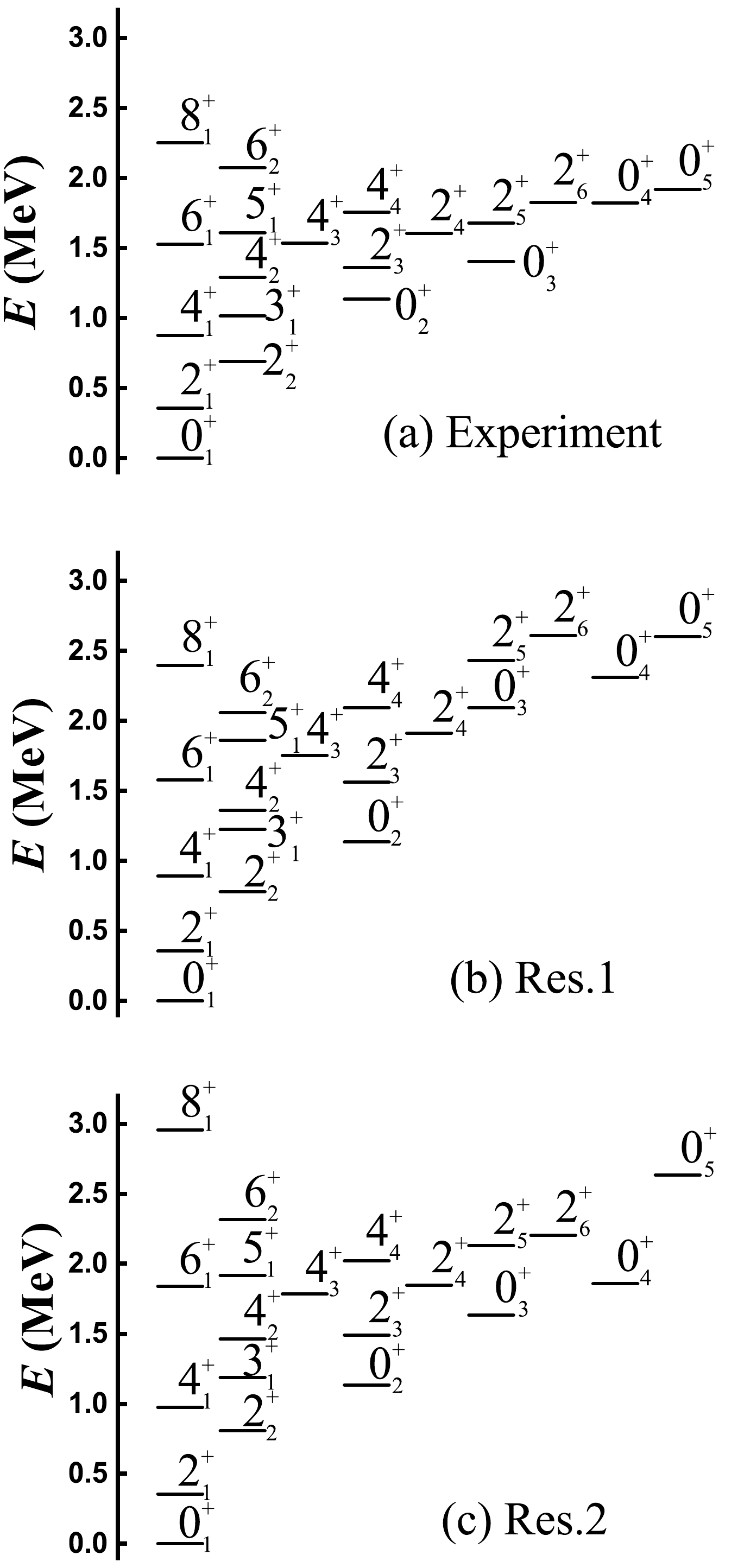
Figure 9. Energy spectra of (a) 196Pt and of the Hamiltonian in Eq. (3) at point B (b) and when adding the fourth-order interaction when
$ \xi=0.05 $ for$ N=6 $ (c).Table 1 lists the
$ B(E2) $ values of some low-lying states in 196Pt, point B (Res.1), the case of adding the fourth-order term (Res.2), the$O(6)$ partial dynamical symmetry model (PDS) [57], the modified soft-rotor model (MSR) [59], and the consistent-Q (CQ) formalism [59]. These previous three models are all related to higher-order interactions in the IBM. In$O(6)$ partial dynamical symmetry, a one three-body interaction that is partially solvable in$O(6)$ symmetry can be constructed, which can mix$ \Sigma =4 $ and$ \Sigma=2 $ , but it does not change the case$ \Sigma =6 $ for$ N=6 $ (Σ is the$O(6)$ label). In the modified soft-rotor model, the higher-order interactions are used to fit the Pt isotopes, which is inspired by the$O(6)$ higher-order symmetry description of 194Pt [58]. For comparison, the CQ results are also listed here. For Res.1, this γ-soft-like description of the point B can exhibit a good consistency with the experimental data qualitatively [60]. From the overall fitting results, it appears somewhat worse than the other two theories, but the result is still reasonable because the parameters of the point B are not adjustable. When the fourth-order interactions are introduced for$ \xi=0.05 $ , the fit can be improved significantly.$ L_{i} $ 

$ L_{f} $ 

Exp. $ ^{a} $ 

Res.1 Res.2 PDS $ ^{b} $ 

MSR $ ^{c} $ 

CQ $ ^{d} $ 

$ 2_1^+ $ 

$ 0_1^+ $ 

40.60(20) 40.6 40.6 40.6 40.6 40.6 $ 2_2^+ $ 

$ 2_1^+ $ 

54(+11 -12) 60.3 43.2 53.0 45.3 50.2 $ 0_1^+ $ 

$<7.8\times 10^{-6} $ 

2.9 5.05 0.27 1.4 0.31 $ 4_1^+ $ 

$ 2_1^+ $ 

60.0(9) 52.6 51.4 53.0 53.6 53.6 $ 0_2^+ $ 

$ 2_1^+ $ 

2.8(15) 3.6 0.122 0.44 3.1 0.55 $ 2_2^+ $ 

18(10) 100.0 79.5 54.1 69.6 51.9 $ 6_1^+ $ 

$ 4_1^+ $ 

73(+4 -73) 52.1 45.3 54.1 54.7 54.7 $ 4_2^+ $ 

$ 4_1^+ $ 

17(6) 34.4 27.4 25.8 18.1 23.8 $ 2_1^+ $ 

0.56(+12 -17) 0.65 1.34 0.14 0.69 0.002 $ 2_2^+ $ 

29(+6 -29) 38.0 31.2 28.3 28.8 28.3 $ 2_3^+ $ 

$ 4_1^+ $ 

0.13(12) 2.34 0.23 0.059 0.60 0.37 $ 2_2^+ $ 

0.26(23) 3.93 3.47 0.19 0.27 0.09 $ 0_1^+ $ 

0.0025(24) 0.025 0.02 0 0.064 0.033 $ 0_2^+ $ 

5(5) 38.3 36.5 17.6 0.003 11.08 $ 0_3^+ $ 

$ 2_1^+ $ 

$<5.0 $ 

0.88 6.82 0 1.05 0.38 $ 2_2^+ $ 

$<0.41 $ 

0.015 0.114 0.41 0.009 1.22 $ 6_2^+ $ 

$ 6_1^+ $ 

16(5) 23.2 17.7 15.3 9.5 0.02 $ 4_1^+ $ 

0.48(14) 0.29 0.77 0.12 0.50 0.0003 $ 4_2^+ $ 

49(13) 42.1 31.9 32.7 32.9 0.008 $ 8_1^+ $ 

$ 6_1^+ $ 

78(+10 -78) 49.1 29.3 47.6 48.5 Table 1. Absolute
$ B(E2) $ values in W.u. for$ E2 $ transitions from the low-lying states in$ ^{196} $ Pt, Res.1 for the cousin point B, Res.2 for adding the fourth-order interaction when$ \xi=0.05 $ , and the PDS and MSR models with effective charge$ e=2.385 $ (W.u.)$ ^{1/2} $ for Res.1 and$e=2.5803$ (W.u.)$ ^{1/2} $ for Res.2.$ ^{a} $ From Ref.[60],$ ^{b} $ From Ref.[57],$ ^{c} $ From Ref.[59], and$ ^{d} $ From Ref.[59].To confirm this conclusion, a quantitative analysis is mandatory. The first quantity that we might study is the staggering parameter
$ S(J) $ in γ band energies [61, 62], defined as$ S(J)=\frac{(E_{J}-E_{J-1})-(E_{J-1}-E_{J-2})}{E_{2_{1}^+}}, $

(10) which quantifies the grouping of adjacent levels within a γ band. Figure 10 presents the
$ S(J) $ for$ J=4,5,6 $ in experimental data, Res.1 and Res.2 in the SU3-IBM, MSR [59], CQ [59], and$O(6)$ symmetry [57]. The black squares are the experimental results. CQ shows the typical γ-soft feature of strong staggering.$O(6)$ , MSR, and Res.1 exhibit similar trends, whereas Res.2 provides the best fitting.The second is on the positions of the
$ 0_{2}^{+} $ ,$ 0_{3}^{+} $ , and$ 0_{4}^{+} $ states in the spectra.$ R'=E_{0_{3}^{+}}/E_{0_{2}^{+}} $ is the energy ratio between the$ 0_{2}^{+} $ and$ 0_{3}^{+} $ states.$ R=E_{0_{4}^{+}}/E_{0_{3}^{+}}-2 $ was used in [57]. Table 2 presents the$ R' $ and R in experimental data, Res.1, Res.2, MSR [59], CQ [59], O(6) symmetry [57], and PDS [57]. For$ R' $ , Res.2, MSR, and CQ can offer reasonable results. For R, Res.1, Res.2, and PDS can provide the best results that are consistent with the experiment data. As shown in [57], although the introduction of higher-order interaction can fit the R well, it increases$ R' $ . Res.2 is the only theory that makes both values more consistent. Note that, because the$ 0_{4}^{+} $ sate in 194Pt is an intruder state [58], the experimental$ 0_{5}^{+} $ (or$ 0_{4}^{+} $ ) state in 196Pt may be also an intruder state.Exp. $ ^{a} $ 

Res.1 Res.2 MSR $ ^{c} $ 

CQ $ ^{c} $ 

O(6) $ ^{b} $ 

PDS $ ^{b} $ 

$ R' $ 

1.236 1.845 1.440 1.131 1.281 1.543 1.786 R −0.701 −0.896 −0.864 −0.192 −0.286 −0.289 −0.629 The experimental data about the quadrupole moments are rare, which are very sensitive to specific nuclear structure models. Table 3 presents the quadrupole moments of some low-lying states in 196Pt, which contain the results of Res.1, Res.2, the MSR model [59], and CQ [59]. The average variance of the fit
$ \Delta Q $ are calculated. Our results are more consistent with the experimental data. The quadrupole moment of these states in the$ O(6) $ limit are all zero with$ \Delta Q=0.64 $ . The quadrupole moments can be a very useful indicator for determining the success of different nuclear models.$ $ 

Exp. $ ^{a} $ 

Res.1 Res.2 MSR $ ^{b} $ 

CQ $ ^{b} $ 

$ Q(2_{1}^{+}) $ 

+0.62 +0.30 +0.70 +0.50 +0.40 $ Q(2_{2}^{+}) $ 

−0.39 −0.48 −0.81 −0.47 −0.37 $ Q(4_{1}^{+}) $ 

+1.03 +0.036 +0.63 +0.66 +0.40 $ Q(6_{1}^{+}) $ 

−0.18 −0.42 +0.35 +0.76 +0.38 $ \Delta Q $ 

0.54 0.39 0.51 0.44 The results of these three quantitative calculations favour the description in terms of SU3-IBM over previous theories.
-
In the traditional understanding of nuclear structure evolution, the collective excitation begins with the phonon excitation mode of the spherical nucleus, just away from the magic number nucleus (the boson number is small). When the boson number increases further, the deformation appears, and then a large deformation gradually emerges, such as the prolate ellipsoid, which is typically characterized by its rotational spectra. Eventually, the γ-soft spectra appear when approaching the next magic nucleus. An authoritative review on this shape phase transitions appeared in 2010 [21]. However, today, these concepts have encountered significant challenges. The spherical nucleus puzzle [63−14] and
$ B(E2) $ anomaly [15−18] dramatically change our understanding of the origin of collectivity in nuclear structure and shape evolutions. If the simple spherical shape does not exist, what collective excitation is it? Additionally, even for magic nuclei, the deformation might already be present [13, 64]. These two peculiar phenomena occur in the collective modes of nuclei with boson number$ N<10 $ . This means that the emergence of collective motions in realistic nuclei will become a more complex problem. An obstinate simple understanding of collective motions in nuclei appears very undesirable. Further experimental information on the two puzzles may provide a more accurate description on nuclear structures. In the SU3-IBM, the spherical shape is replaced by a spherical-like quadrupole deformation, which challenges the traditional perspective.Even for typical large-deformation nuclei as 154Sm and 166Er, new studies have found that the structure of 154Sm exhibits the coexistence of prolate and triaxial shapes, whereas the deformed shape with a strong triaxial instability is demonstrated on 166Er, which has been shown to be related with the self-organization mechanism [65, 66]. This perspective appears to be very attractive. In the traditional understanding, 154Sm and 166Er are typical nuclei with a prolate shape with
$ \beta/\gamma $ vibrational excitations for the rotational spectra exists. However, recently, some nuclear structure models have been used to investigate the nature of 166Er [65, 67, 68]. The studies found that the ground state of this largely-deformed nucleus has triaxial deformation with$ \gamma\approx 9^{\circ} $ . Otsuka et al. argued that the triaxial shapes dominate in the heavy nuclei [69]. These studies questioned the prolate predominance and placed the triaxial shapes in a much more important position.In our study on the prolate-oblate asymmetic shape phase transition [4], only the SU(3) second-order (prolate shape) and third-order (oblate shape) Casimir operators
$ \hat{C}_{2}[{S U(3)}] $ ,$ \hat{C}_{3}[{S U(3)}] $ were considered. In the SU(3) limit, the prolate shape is described by the SU(3) irrep (2N,0), whereas the oblate shape is (0,N). However, these are not sufficient. In this paper, using 196Pt as an example, the square of the SU(3) second-order operator$ \hat{C}_{2}^{2}[{S U(3)}] $ is necessary. Ref. [5] showed that this fourth-order interaction is vital for the triaxial shape. A new study showed that 196Pt may be related with the SU(3) irrep (4,4) [70]. From the perspective of Otsuka et al. [65, 67, 69], this interaction may be also important for other nuclei, even the prolate nuclei 180Hf. This shape phase transition requires further studies, and the SU3-IBM can also be used to study the triaxiality of these large deformation nuclei. For 166Er, if$ \gamma\approx 9^{\circ} $ , the ground state has the SU(3) irrep (22,4), which can be easily treated using the SU3-IBM. Note that every quadrupole deformation is treated equally in the SU3-IBM, which differs from previous models with SU(3) symmetry.In addition to spherical and prolate nuclei, we questioned the O(6) description of the γ-soft nuclei in Refs. [4, 6]. This article can be considered an extension of the previous studies [1, 4]. These papers proposed the SU3-IBM, which was inspired by the interesting findings in Refs. [25, 26]. When only the
$ U(5) $ and$ {{S U}}(3) $ limits are considered, a γ-soft-like rotational mode can also occur as an emergent phenomenon if the$ {{S U}}(3) $ higher-order interactions are introduced into the common formalism. This differs significantly from the γ-softness related to the$O(6)$ limit. In the traditional IBM,$O(6)$ symmetry is exactly solvable, and γ-unstable spectra can be expected. The SU3-IBM in particular can describe the$ B(E2) $ anomaly, which makes the model useful. If triaxiality dominates in heavy nuclei, it can further support the SU3-IBM.Since the inception of the γ-independent solution in the geometric model [41], it has been considered as one of the paradigms in nuclear structure, alongside the spherical and axially-deformed cases. The behavior of the potential in the γ variable can range from the extreme case of γ-independent potential to the γ-rigid case, passing through the intermediate case of γ-soft. In the soft cases (and up to complete γ-independence), the fluctuations in triaxiality might be very large, which makes the shape of a γ-soft nucleus much more difficult to understand with repsect to the spherical and axial cases. The ideal O(6) symmetry implies complete γ-instability [20], and believing that nuclei might achieve it, even only approximately, is unrealistic. The problem results from
$ \overline{ {S U(3)}} $ symmetry in Hamiltonian (1), and the O(6) symmetry point is considered the critical point between the proalte and oblate shapes [23, 24].$ \overline{ {S U(3)}} $ symmetry has the same spectra as SU(3) symmetry [22]. However, this spectral symmetry cannot be found in realistic nuclei, which presents many constraints on the shape evolution from the prolate to oblate shape. Ref. [4] found that this shape evolution is asymmetric. Therefore,$ \overline{ {S U(3)}} $ symmetry cannot be achieved, and O(6) symmetry, albeit attractive from a mathematical perspective, cannot be easily attained in realistic nuclei that can be γ-soft but not fully γ-unstable. Of course, this requires further evidence.In the SU3-IBM, the γ-softness results from the combinations of the d boson number operator and the rigid quadrupole defomations described by the SU(3) interactions. Thus, it is an emergent phenomenon and different from the one with O(6) symmetry.
Figure 11 presents partial energy spectra of 120Cd, 196Pt, and 132Ba, whose boson numbers are all
$ N=6 $ . Ref. [10] obtained the spectra of 120Cd, in which the$ 0_{3}^{+} $ state at the three-phonon level is absent. The energy of the$ 0_{3}^{+} $ state of 120Cd is predicted by our theory to be approximately 2300 keV or even higher. Thus, this is a new γ-soft rotational mode [8, 9, 12] despite it appearing much like the rigid spherical vibrational excitation mode. If we consider that the IBM can truly describe the collective excitations in realistic nuclei, the only way to describe the new γ-soft behaviors is to introduce the$ {{S U}}(3) $ higher-order interactions. The theory functions better than expected [1−3].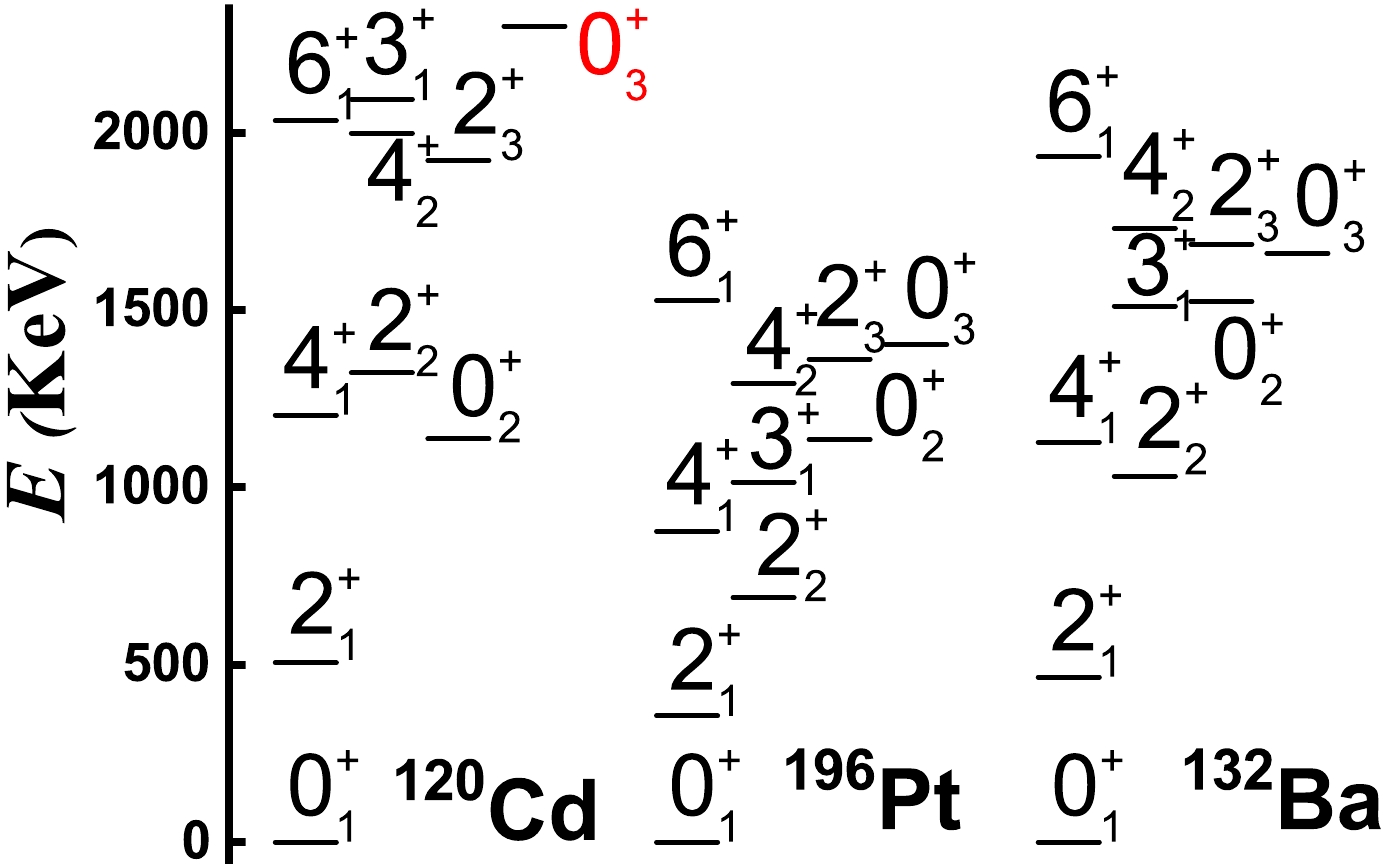
Figure 11. Partial energy spectra in 120Cd normal states, 196Pt and 132Ba [71]. The energy of the
$ 0_{3}^{+} $ state in the 120Cd normal states is predicted by the authors.196Pt and 132Ba are two typical traditional γ-soft nuclei. In the IBM, this type of γ-softness is related to
$O(6)$ or$O(5)$ symmetry, such as$E(5)$ critical point description [72, 73]. In practice, this case is not related to the deformation γ parameter. The SU3-IBM follows the principle that triaxiality results from the competition between the prolate and oblate shapes. In this paper, we show that the new emerging γ-softness can resemble the traditional γ-soft spectra and their$ B(E2) $ behaviors. When other$ {{S U}}(3) $ higher-order interactions are introduced, the fitting of spectra appears excellent. This will be further discussed in subsequent papers.This principle requires some additional clarifications. The sign of the electric quadrupole moment of the
$ 2_{1}^{+} $ state in a realistic nucleus provides a robust characteristic of the shape. If the sign is negative, it is a prolate shape or prolate-biased triaxiality, whereas a positive sign indicates that it is an oblate shape or oblate-biased triaxiality. For realistic nuclei, the sign can change from negative to positive, and triaxiality must play an essential role for understanding the shape revolution [4]. The SU3-IBM is particularly suitable for discussing the evolution of the quadrupole deformations because these shapes can be explicitly and directly given by the SU(3) irrep$ (\lambda, \mu) $ . In the SU3-IBM, the evolution from the prolate to oblate shape can easily include the triaxial shapes, and many evolutional paths including triaxiality exist. Even for the SU(3) degenerate point, it contains various possible quadrupole deformations [1, 26]. When$ \hat{C}_{2}^{2}[{S U(3)}] $ is introduced, the ground state can have a certain rigid triaxial shape in the SU(3) limit [5]. It should be noticed that$ \hat{C}_{2}^{2}[{S U(3)}] $ can not describe the triaxiality alone, and should be used with the$ \hat{C}_{2}[{S U(3)}] $ ,$ \hat{C}_{3}[{S U(3)}] $ interactions.$ \hat{C}_{2}^{2}[{S U(3)}] $ can cause complicated shape evolutions, which requres more investigations in the future. If triaxiality dominates in the heavy nuclei, this principle would be even more important.In previous discussions, spectra and low-lying
$ B(E2) $ values of various γ-soft rotational modes in different nuclear structure theories are very similar. Therefore, distinguishing various γ-softness in different theories is becoming extremely important. New γ-softness in the normal states of Cd nuclei can be described only using the SU3-IBM. However, the spherical nucleus puzzle is still being debated [13, 14, 74, 75]. A detailed study on$ ^{108-120} $ Cd with other SU(3) higher-order interactions was recently performed [76]. A complete description of$ ^{110,112} $ Cd including configuration mixing, like Refs. [77−81], is in progress.$ B(E2) $ values between higher levels are useful, such as the$ 0_{3}^{+} $ ,$ 2_{4}^{+} $ , and$ 2_{5}^{+} $ states. Quadrupole moments of the low-lying states may provide significant value in distinguishing the various models.Although extensive theoretical work is still required, we expect that many observations in γ-soft-like nuclei might be described by the SU3-IBM in a unified manner.
$E(5)$ -like γ-softness in 82Kr is found in the new model [5]. Each interaction in the SU3-IBM has a clear geometric meaning and differs from common considerations in microscopic theory, such as SD-pair shell model [82, 83]. In the microscopic theory, various deformations resulting from the proton-neutron interactions can result in different deformation shapes, including the γ-soft rotational mode [84, 85]. This does not occur in the SU3-IBM; a specific interaction corresponds to a certain shape, and the γ-softness is an emergent phenomenon, which cannot be expected before numerical calculations. Understanding this point is an interesting problem. From the existing results, the SU3-IBM is closer to the geometric collective model [50]. The emerging γ-softness in the geometric model might be an important topic to investigate [86, 87].Since the seminal research by Elliott [88−90],
$ {{S U}}(3) $ symmetry has played an essential role in describing the rotational spectra from the perspective of a microscopic shell model [36, 91−103].$ {{S U}}(3) $ symmetry is essential in describing shell-like quartetting of nucleons, and the$ {{S U}}(3) $ third-order Casimir operator$ \hat{C}_{3}[{S U(3)}] $ is required to describe the experimental spectra to distinguish between the prolate and oblate shapes [104−107]. In previous studies,$ {{S U}}(3) $ symmetry was related to the prolate shape. In our new findings ([1−6] and this paper), the$ {{S U}}(3) $ symmetry actually dominates all the quadrupole deformations. In particular, in this model, we can obtain large quadrupole moments, even with spectra that resemble a γ-soft situation. We expect that this new perspective can be further used in the pseudo-$ {{S U}}(3) $ shell model [94, 95].Along the dashed red line through points A and B, shape phase transition from the prolate to oblate shape has been studied [4], and this is an asymmetric evolution, which differs from the symmetric one in
$ \hat{H}_{1} $ [23, 24]. The study of the properties of 196Pt in this paper further supports this perspective and a more detailed investigation on the prolate-oblate shape phase transition is also needed.In addition, in Ref. [5], the
$ \rm E(5) $ -like energy spectrum was also found in the new model, which contains some new findings pointing to the γ-softness. These findings are further used to understand 196Pt, which will be given in the second part (II) of the discussions [70].The rigid triaxial rotor in nuclear structure was first studied by Davydov and Filippov [108]. In the SU(3) shell model, a SU(3) mapping of the rigid triaxial rotor can be obtained, which bridges the geometrical and shell models [109−111]. This SU(3) mapping was also discussed in the IBM [31, 32]. Twenty years ago, Wood et al. investigated the triaxial rotor model by relaxing the use of irrotational moments of inertia [112]. Subsequently, this model was used to describe the
$ E2 $ matrix elements available for$ ^{186,188,190,192} $ Os [113], which were often treated as γ-soft nuclei. Importantly, the nearly zero value of the B(E2) transition from the$ 2_{2}^{+} $ to$ 0_{1}^{+} $ state in 196Pt can be explained by this model [114]. These can enable us to further improve the fitting of 196Pt.SU3-IBM makes the SU(3) symmetry become even more important. In previous studies, the SU(3) symmetry was primarily related to the prolate shape and its rotational spectra [36]. In the SU3-IBM, the SU(3) symmetry has relationships with all the quadrupole deformations. Although this interpretation is very simple, it was not achieved before. In the SU(3) mapping of the rigid triaxial rotor, the SU(3) higher-order interactions are discussed [109−111], but they are not used to discuss the γ-softness in realistic nuclei. For the proxy-SU(3) symmetry, the energy shells for medium and heavy nuclei are reconsidered as Elliott's SU(3) symmetry shells [102, 103]. Thus, SU(3) symmetry also dominates the higher shells, and the many-nucleons states can be described using SU(3) symmetry. This is a breakthrough for understanding the single particle features. The proxy-SU(3) symmetry was also used to discuss the asymmetric prolate-oblate shape phase transition. This phenomenon can be explained by the short-range nature of the nucleon-nucleon interaction, which leads to the dominance of the highest weight SU(3) irrep. We believe that, if the SU(3) higher-order interactions are considered here, new triaxial shape may be obtained. These results are somewhat consistent with our conclusions. The proxy-SU(3) symmetry appears to provide a microscopic foundation for the SU3-IBM. The proxy-SU(3) shell models with SU(3) higher-order interactions will be discussed in the future, and the mapping of the SU3-IBM from the proxy-SU(3) shell model should be also investigated.
The degree of γ-rigidity or γ-softness is determined by the fluctuation in the γ degree of freedom. Therefore, clearly distinguishing between them is difficult. In our new study, we found that γ-soft spectra can result from the γ-rigid ones [70]. In the geometric model, the Z(5) critical point symmetry was proposed to describe the critical nucleus from the prolate to oblate shape [115], in which it is somewhat γ-rigid with
$ \gamma=30^{\circ} $ . In addition, the equivalence between γ-soft and rigid triaxiality with$ \gamma=30^{\circ} $ has been studied at the O(6) limit of IBM using projection techniques [116, 117]. These questions require further study after our second paper [70].In the SU(3) mapping,
$ [\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ ,$ [(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ , and$ \hat{L}^{2} $ are used to describe the rotational spectrum of the rigid triaxial rotor, but they cannot affect the positions of the$ 0^{+} $ states. In this paper, we show that the$ 0^{+} $ states can be adequately explained by introducing the SU(3) third-order$ \hat{C}_{3}[{S U(3)}] $ and fourth-order interactions$ \hat{C}_{2}^{2}[{S U(3)}] $ . Thus, introducing$ [\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ and$ [(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ will further improve the fitting of the B(E2) values in Table I. SU(3) mapping of the research of Wood et al. [112−114] will be first required. These will be given in the third and fourth parts (III and IV) of the discussion. -
Recently, the interacting boson model with
$ {{S U}}(3) $ higher-order interactions (SU3-IBM) was proposed [1−3] to resolve the spherical nucleus puzzle [8−14],$ B(E2) $ anomaly [15−18], and prolate-oblate asymmetric shape evolution [4, 23, 24]. Although this model can be obtained by considering only the$ U(5) $ and$ {{S U}}(3) $ limits, the γ-soft-like rotational mode can emerge. These results may extend our understanding of the interacting boson model (IBM). As stated by Heyde and Wood, “sphericity is a special case of deformation,” and “the reference frame must be fundamentally one of a deformed many-body system.” [11]. The emerging γ-softness may have an essential role in the shift of perspective.Following previous studies [1, 4], the emerging γ-soft-like rotational mode can be explored to explain the properties of 196Pt. In our studies, we explore a special point, which is near the middle point of the degenerate line connected the
$ U(5) $ limit and$ {{S U}}(3) $ degenerate point. The objective of this study was only to explore the relationship between the emerging γ-softness and γ-soft properties in realistic nuclei. Further detailed fitting will be conducted in the future when other$ {{S U}}(3) $ higher-order interactions are introduced, which is related to the destructive interference in the triaxial rotor model [112−114].Further investigation of the γ-rigid triaxiality is also important in the SU3-IBM. This is a delicate topic [48]. The phase diagram of the SU3-IBM will be given in the future as it can offer meaningful guidance to the rigid triaxiality. Additionally, 6-d interaction may be valuable [28, 29]. Distinguishing between the different γ-softness and discussing the differences between the γ-softness and the rigid triaxiality are topics that require further exploration.
Finally, a direct discussion and fitting of the new model on the oblate nuclei, such as
$ ^{196-204} $ Hg, is extremely important for understanding the SU3-IBM and establishing the relationship between the new and$ {{S U}}(3) $ shell models. A discussion on the triaxiality of 166Er with SU3-IBM will be also considered in the future.
Emerging γ-soft-like spectrum in 196Pt in the SU3-IBM (I)
- Received Date: 2024-03-04
- Available Online: 2024-09-15
Abstract: Recently, studies have argued that a spherical-like spectrum emerges in the SU3-IBM, thus creating new approaches to understanding γ-softness in realistic nuclei. In a previous study, γ-softness with degeneracy of the ground and quasi-γ bands was observed. In this paper, another special point connected to the middle degenerate point is discussed. It is found to be related to the properties of 196Pt. This emergent γ-softness is also shown to be important for understanding the prolate-oblate asymmetric shape phase transition. The low-lying spectra,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: