-
In the past several decades, the reactions induced by weakly bound nuclei around the Coulomb barrier have been extensively examined in both theoretical and experimental fields [1–6]. Due to the relatively strong cluster structure and low breakup threshold, the reaction mechanisms become more complicated when weakly bound nuclei are involved. These weakly bound nuclei include both unstable and stable types. Compared to unstable ones, the beam intensities of stable weakly bound nuclei are orders of magnitude higher. Thus, numerous experiments have been performed to explore the reaction mechanisms induced by stable weakly bound nuclei, especially 6Li, 7Li, and 9Be.
Based on the systematic comparison of experimental results for the fusion process induced by 6Li, it can be shown that the complete fusion (CF), defined by the fully captured of projectile by the target, is suppressed by
$\sim$ 30% at energies above the Coulomb barrier when compared with the coupled channel (CC) calculation, which cannot consider the coupling of breakup reaction. When the cross section of incomplete fusion (ICF) process (only part of projectile is captured by the target) is added to the CF, the total fusion (TF) cross sections are in agreement with the CC calculation, indicating that the missing flux for CF process actually produces ICF residues [7–13]. Thus, the suppression factor can also be fully defined by experimental observables, specifically the ratio between CF and TF cross sections. However, the transfer process, particularly cluster or proton transfer, can produce the same residues as the ICF process, making it difficult to distinguish between these two processes experimentally. This point should be emphasized when dealing with any measured ICF cross section.Furthermore, it is higly interesting to examine the coupling effect of transfer on the fusion or breakup process induced by the 6Li. It is well known that 6Li has a significant α + d structure in the ground state. Hence, in many experimental studies, attempts have been made to determine the origin of large yielded α particles from the reaction. A series of publications [14–16] reported that the direct breakup provides only a small contribution, and the dominant contributor is the breakup following transfer, i.e., "resonant breakup". Meanwhile, the influence of resonant breakup on the CF process strongly depends on the lifetime of the resonant state produced in the transfer reaction. This dependence means that no solid conclusion can be drawn solely based on experimental results. Moreover, a recent study [17] proposed that the dominant process that leads to CF suppression is direct cluster transfer of weakly bound nuclei.
On the other hand, the neutron-transfer excitation functions do not drop as fast as the fusion excitation function at sub-barrier energies. This phenomenon has been observed in 9Be + 169Tm, 181Ta, 187Re [18] systems. On medium mass target nuclei, the one-neutron stripping cross section of 6Li + 96Zr [19] and 6Li + 89Y [20] were measured to investigate the effect of transfer on fusion. For 6Li + 96Zr system, the one-neutron stripping cross sections are much smaller than the CF cross sections above the Coulomb barrier and exhibit the same magnitude as the CF cross section around the Coulomb barrier. For 6Li + 89Y, it is concluded that the neutron transfer reaction may contribute significantly to the total reaction cross sections at energies close to and below the Coulomb barrier.
In this study, we report on an experimental study on 6Li + 94Zr, showing all the measured CF, ICF, and one-neutron transfer cross sections around the Coulomb barrier. Hence, the complicated reaction mechanisms induced by 6Li on medium mass target are investigated further. This paper is organized as follows: Sec. II describes the experimental results. The discussions and comparisons with the results of the theoretical calculations are presented in Sec. III. The summary is given in Sec. IV.
-
The 6Li + 94Zr experiment was performed at HI-13 Tandem Accelerator of China Institute of Atomic Energy (CIAE) [21]. The 6Li3+ beams were produced at six energies corresponding to 29.9, 23.9, 21.9, 17.9, 15.8, and 13.8 MeV. This beam energy ranged from below to above the 16.4-MeV Coulomb barrier at the laboratory frame. The beam intensities were recorded by a Faraday cup placed after the target using a precision current-integrator device. The beam intensities varied from 17.1 to 36.7 enA during the entire experiment.
A 91.2% enriched 94ZrO2 foil with a thickness of 481 μg/cm2 was used as the target. A 2.07-mg/cm2 gold backing exists behind the target to stop all the residues. The 94Zr target was placed at the center of the HPGe detector array. The HPGe detector array was used to detect γ rays emitted by reaction products and comprised 6 HPGe detectors surrounded by BGO crystal for Compton suppression (BGO-HPGe), 2 planar-HPGe, and 2 Clover. All the detectors are fixed at five angles: 2 BGO-HPGE and 2 Clover at 90°, 2 BGO-HPGe and 1 planar at 42°, 1 planar at 120°, 1 BGO-HPGe at 150°, and 1 BGO-HPGe at 153°. The efficiency and energy calibrations were realized by 152Eu and 133Ba sources with known radioactivity placed at the target position. The absolute efficiency of the entire detector array was 0.6% and the energy resolution was 3 keV at 1000 keV. The digital data acquisition system XIA was used to record the data. Detailed descriptions of this digital data acquisition system have been presented in Ref. [22].
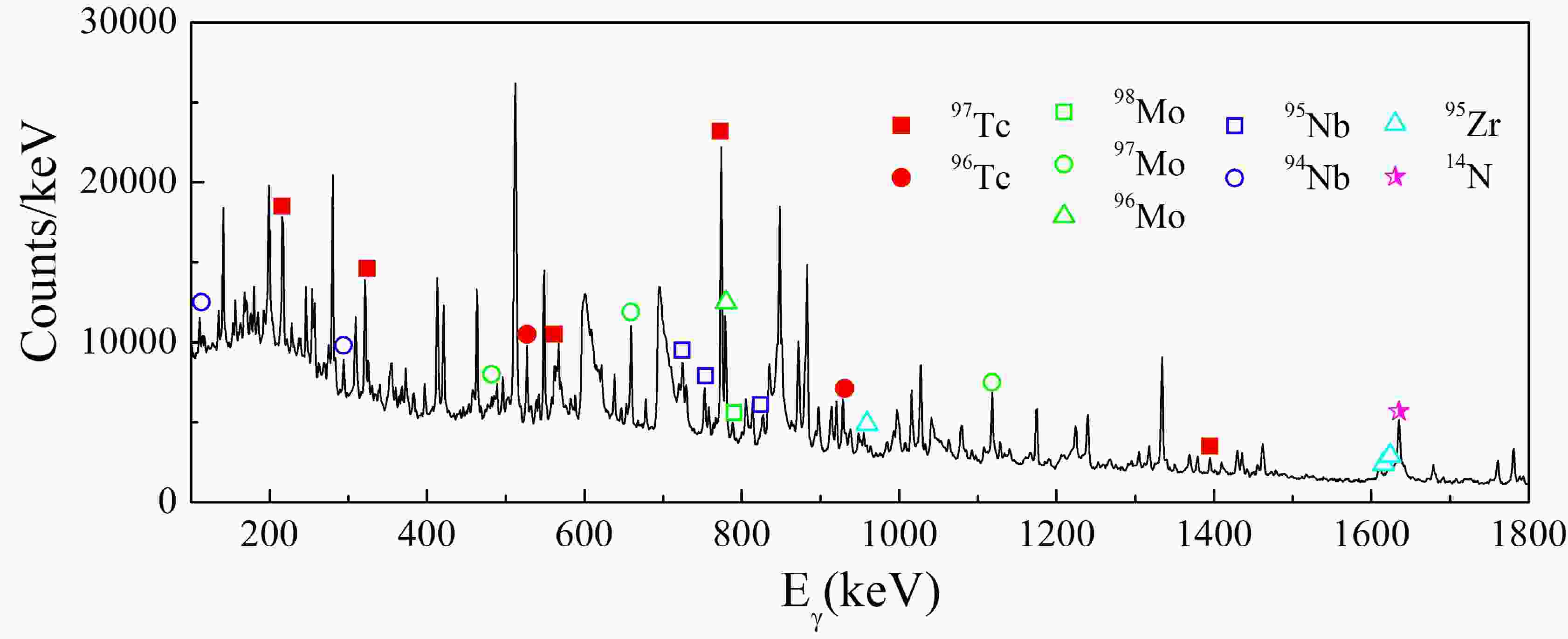
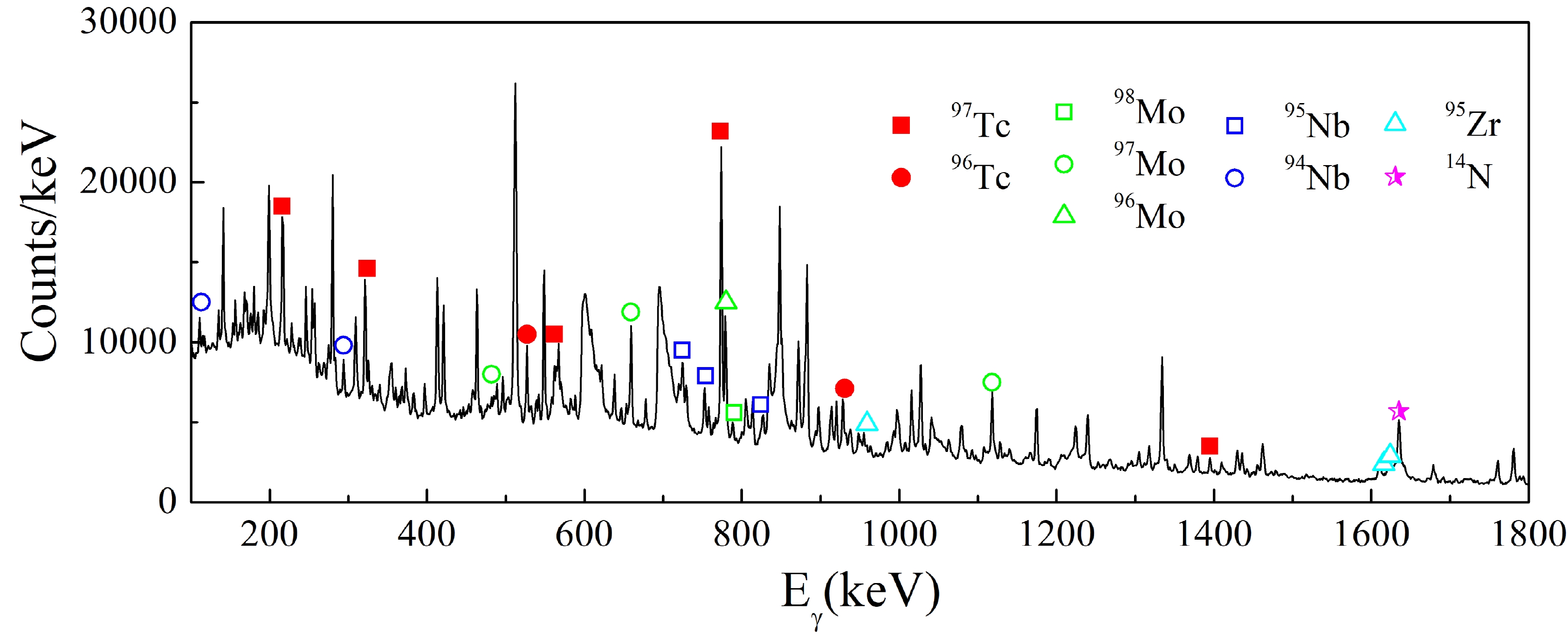
Figure 1 shows a typical online single γ ray spectrum at Elab = 29.9 MeV. The identified characteristic γ rays in 97, 96Tc, 98, 97, 96Mo, and 95, 94Nb, obtained from fusion process, can be observed clearly. The cross section for the online γ method is calculated using this relation:
$ \sigma = \frac{1}{N_B N_T}\left [ \sum\limits^n_{i=1} \frac{N_{\gamma i} (1+F_{\gamma i})}{\varepsilon_{\gamma i } } \right ]. $

(1) Specifically, n denotes the number of γ transitions feeding the ground state or long lived isomer for one residue. Nγi denotes the yield of γ transitions. Furthermore,
$ \varepsilon_{\gamma i } $ denotes the absolute efficiency of all detectors for γ ray. Fγi denotes the inner conversion electron rate. Additionally, NB and NT denote the total numbers of incident beam particles and target nuclei per unit area, respectively. The total uncertainty for cross section included statistical errors of the yields of γ rays, number of incident particles, and 5% systematic error of target thickness.Here, γ transitions, which are solely used to obtain the cross section for each residue, are marked with different labels and listed in the Table 1. The measured cross sections of each residue are summarized in Table 2.
Residue Transition Eγ/keV 97Tc $ 5/2^- \rightarrow 1/2^- $ 

561 $ 5/2^+ \rightarrow 9/2^+ $ 

325 $ 7/2^+ \rightarrow 9/2^+ $ 

216 $ (9/2^+) \rightarrow 9/2^+ $ 

862 $ 11/2^{(+)} \rightarrow 9/2^+ $ 

833 $ 13/2^+ \rightarrow 9/2^+ $ 

773 $ (13/2^+) \rightarrow 9/2^+ $ 

1393 96Tc $ 7^+ \rightarrow 6^+ $ 

526 $ 9^+ \rightarrow 7^+ $ 

927 98Mo $ 2^+ \rightarrow 0^+ $ 

787 97Mo $ 3/2^+ \rightarrow 5/2^+ $ 

481 $ 7/2^+ \rightarrow 5/2^+ $ 

658 $ 9/2^+ \rightarrow 5/2^+ $ 

1117 96Mo $ 2^+ \rightarrow 0^+ $ 

778 95Nb $ 7/2^+ \rightarrow 9/2^+ $ 

757 $ 7/2^+ \rightarrow 9/2^+ $ 

724 $ (13/2^+) \rightarrow 9/2^+ $ 

825 94Nb $ (3)^+ \rightarrow 3^+ $ 

293 $ (5)^+ \rightarrow 6^+ $ 

113 95Zr $ 1/2^+ \rightarrow 5/2^+ $ 

954 $ (3/2)^+ \rightarrow 5/2^+ $ 

1618 $ (5/2^+) \rightarrow 5/2^+ $ 

1625 Table 1. Characteristic γ rays used to extract cross sections.
Residue 29.9 MeV 23.9 MeV 21.9 MeV 17.9 MeV 15.8 MeV 13.8 MeV 97Tc $ 375.7 \pm 20.4 $ 

$ 326.0 \pm 15.0 $ 

$ 220.4 \pm 9.5 $ 

$ 24.1 \pm 1.3 $ 

$ 3.7 \pm 0.2 $ 

96Tc $ 93.3 \pm 6.2 $ 

$ 2.7 \pm 0.3 $ 

98Mo $ 8.1 \pm 0.8 $ 

$ 18.1 \pm 1.7 $ 

$ 16.3 \pm 1.5 $ 

97Mo $ 127.3 \pm 8.1 $ 

$ 84.1 \pm 5.1 $ 

$ 59.4 \pm 3.6 $ 

$ 12.0 \pm 0.7 $ 

$ 3.9 \pm 0.4 $ 

96Mo $ 94.2 \pm 8.7 $ 

$ 26.6 \pm 2.5 $ 

$ 14.8 \pm 1.4 $ 

$ 5.0 \pm 0.5 $ 

$ 2.7 \pm 0.3 $ 

$ 1.9 \pm 0.2 $ 

95Nb $ 62.2 \pm 3.5 $ 

$ 70.7 \pm 3.9 $ 

$ 66.6 \pm 3.6 $ 

$ 49.5 \pm 2.7 $ 

$ 23.0 \pm 1.3 $ 

$ 5.1 \pm 0.3 $ 

94Nb $ 45.6 \pm 3.4 $ 

$ 26.2 \pm 1.9 $ 

$ 23.0 \pm 1.7 $ 

$ 0.8 \pm 0.1 $ 

TF $ 806.3 \pm 24.9 $ 

$ 554.4 \pm 16.6 $ 

$ 400.4 \pm 11.2 $ 

$ 91.6 \pm 3.1 $ 

$ 33.3 \pm 1.3 $ 

$ 7.0 \pm 0.3 $ 

R $ 85.7\pm 5.5\% $ 

$90.3 \pm 6.3\% $ 

$91.8 \pm 4.0\% $ 

$94.2 \pm 3.5\% $ 

$95 \pm 2.8\% $ 

CF $ 547.4 \pm 43.0 $ 

$ 364.0 \pm 30.3 $ 

$ 240.1 \pm 14.8 $ 

$ 25.6 \pm 1.7 $ 

$ 3.9 \pm 0.2 $ 

ICF $ 258.9 \pm 49.7 $ 

$ 190.4 \pm 34.6 $ 

$ 160.3 \pm 18.5 $ 

$ 65.9 \pm 3.5 $ 

$ 29.4 \pm 1.4 $ 

$ 7.0 \pm 0.3 $ 

95Zr (954 keV) $ 15.3 \pm 2.7 $ 

$ 20.1 \pm 3.3 $ 

$ 18.4 \pm 2.8 $ 

$ 12.2 \pm 2.0 $ 

$ 6.5 \pm 1.1 $ 

95Zr (1618 keV) $ 10.7 \pm 2.0 $ 

$ 13.5 \pm 2.3 $ 

$ 12.8 \pm 2.0 $ 

$ 10.3 \pm 1.7 $ 

$ 4.6 \pm 0.8 $ 

95Zr (1625 keV) $ 13.8 \pm 2.5 $ 

$ 20.0 \pm 3.3 $ 

$ 19.0 \pm 3.0 $ 

$ 16.3 \pm 2.7 $ 

$ 7.8 \pm 1.3 $ 

95Zr (total) $ 39.8 \pm 4.2 $ 

$ 53.6 \pm 5.2 $ 

$ 50.2 \pm 4.6 $ 

$ 38.8 \pm 3.8 $ 

$ 18.9 \pm 1.9 $ 

Table 2. Cross sections for each residue. The unit for a cross section is mb.
It should be noted that the level scheme for odd-odd nucleus is more complicated. Some low-lying states states of 96Tc and 94Nb, were not be counts in the data analysis. According to theoretical assessment(based on the method introduced in Ref. [23]), approximately 15% and 6% cross sections of 96Tc and 94Nb were disregarded, respectively.
In addition to the fusion reaction channels, the one-neutron stripping reaction channel was also observed in this experiment. For 6Li + 94Zr system, the residue of one-neutron stripping process is 95Zr. The observed γ transitions of 95Zr are denoted in Fig. 1 and the details are listed in Table 1. In the experiment, the cascading γ transitions of the 954, 1618 and 1625 keV γ transitions were not observed. It means the 954, 1618 and 1625 keV pure single nucleon states in 95Zr were populated which are consistent with the states observed in the single nucleon transfer reaction. If the β decay of 95Y and fusion evaporation process populate the 95Zr, the de-excited γ transition from the excited state with higher spin should be observed. Therefore, the influence of other reaction channels on 95Zr can be excluded. Correspondingly, the direct production cross sections of each excited state of 95Zr were derived by the yield of the corresponding decay γ transitions.
-
Based on the cross sections measured for each residue as listed before, the cross sections for different processes, such as CF and ICF, should be identified first. Then, a detailed discussion can be provided according to the systematic comparison or theoretical calculation. The following two subsections will show a detailed investigation on the fusion and one-neutron transfer process in the 6Li + 94Zr reaction.
-
Before delving into details on the separation between CF and ICF process, the TF cross section can be easily derived by adding the cross sections of all fusion residues. The compound nucleus formed by the CF reaction between 6Li and 94Zr is 100Tc. Specificially, 100Tc decays predominantly by 3n, 4n evaporation channels, generating 97Tc and 96Tc, respectively. It is well known that in this medium mass region, the CF compound nucleus can also evaporate charged particles, such as proton and α, producing same residues with ICF process. Therefore, the CF and ICF cannot be separated exactly when only relying on the experimental result.
Meanwhile, in fusion reaction, the ratio between different residues can be reasonably predicted via a statistical model [11, 12] such as PACE4 [3]. R =
$\sum\sigma_{\rm Tc}^{\rm PACE}/\sigma_{\rm fus}^{\rm PACE}$ was obtained by the result from PACE4 calculation, showing the contribution of neutron evaporation channels from the compound nuclide (100Tc) in the 6Li + 94Zr complete fusion reaction. Here,$\sum\sigma_{\rm Tc}^{\rm PACE}$ is the sum of PACE4 predicted cross sections for Tc isotopes, and the$\sigma_{\rm fus}^{\rm PACE}$ represents the fusion cross section estimated by the same code. Accordingly, the experimental CF cross sections can be deduced by dividing the cumulative measured cross sections of Tc isotopes$\sigma^{\rm expt}_{\rm Tc}$ by ratio R. With the measured TF (as mentioned at the beginning the current subsection) as well as the deduced CF cross section, the cross section for ICF can be derived ICF = TF - CF. The ratio R calculated by PACE4 at different beam energy are shown in Table 2. The level density parameter was set as a = A/10 in the PACE4 calculation according to the systematic study performed in Ref. [24]. The error of R was introduced when a varied from a = A/9 to a = A/12 referring to the value in Refs. [25–27].Hence, the deduced cross sections for TF, CF, and ICF for the current 6Li + 94Zr reaction are summarized in Table 2 and Fig. 2. As mentioned in the introduction, the suppression factor of CF was obtained by the comparison with CC calculation without the coupling of breakup channel. In this case, the cross section of CC calculation is total fusion cross section. Hence, the suppression of CF can be obtained by the relative ratio of CF to TF. In Fig. 2, it can be observed that there is 30% suppression of CF cross section above the Coulomb barrier when compared with the TF, which is consistent with the systematic behaviour for the fusion process induced by 6Li. Additionally, it should be emphasized that the ICF cross-section may include contribution of some transfer processes due to the limit of the current experiment method, such as one proton stripping process.
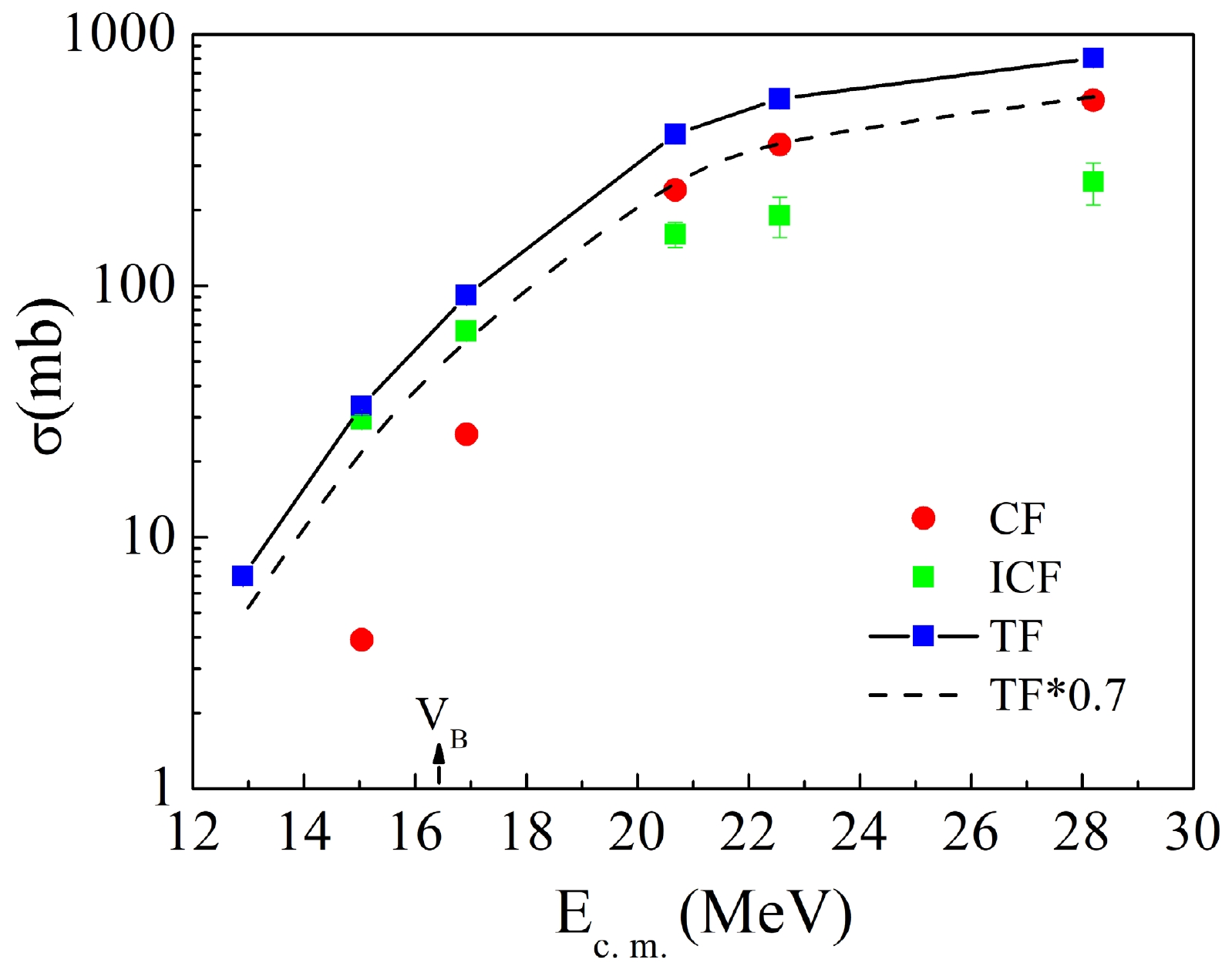
Figure 2. (color online) Summary of CF, ICF cross sections obtained in the current 6Li + 94Zr reaction.
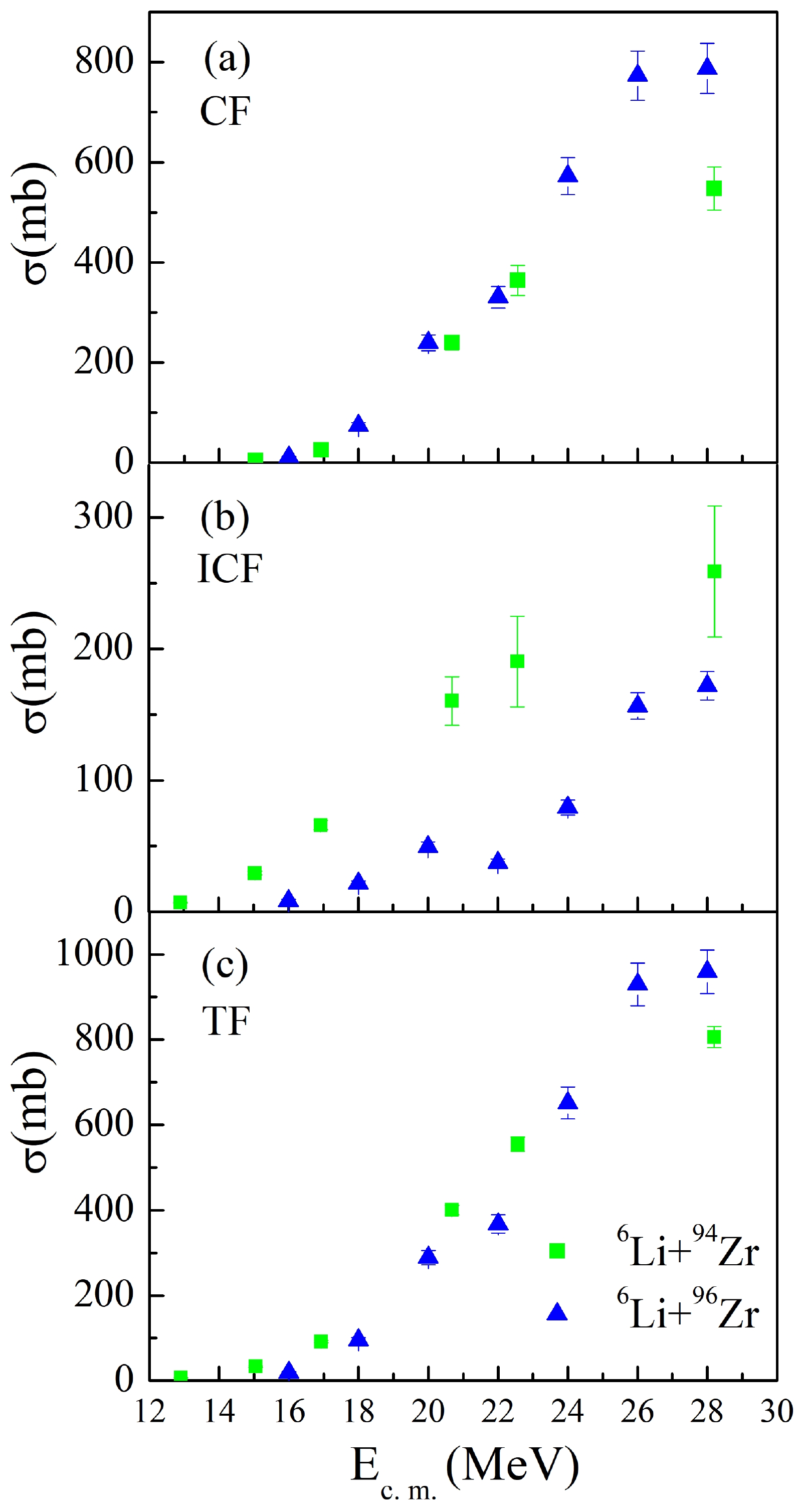
Furthermore, the new cross sections are compared with that from 6Li + 96Zr reaction (data obtained from Ref. [11]) with an emphasis on the above-barrier region. In Fig. 3(c), it can be observed that the two systems exhibit quite similar TF cross sections even though the cross section for 6Li + 96Zr system shows an anomalous increment at 26 MeV. However, the ICF cross section is significantly larger in 6Li + 94Zr system as shown in Fig. 3(b) among the whole measured energy region. This is consistent with the phenomenon that the CF cross section is slightly lower for 6Li + 94Zr system at the above-barrier region as shown in Fig. 3(a).
Considering the fact that the ICF cross section can be ill-defined in experiment since the other reaction channels may contribute to the same residues, such as single-proton transfer reaction (producing the same residues with the deuteron-captured ICF process by evaporating one neutron), which would affect the TF cross section as well. Thus, the best candidates for the systematic comparison would be the CF cross section which is solely deduced from Tc isotopes. Fig. 4 compares the CF cross sections between 6Li + 90, 94, 96Zr systems. Due to the dynamic effect from the coupling of breakup or transfer and the static effect originated from the deformation or cluster structure, the systematic study of fusion cross sections becomes quite difficult. As mentioned in Ref. [28], to obtain a better understanding of the contribution from the breakup process on the fusion reactions, induced by weakly bound nuclei, the reduced CF cross sections F(x) can be obtained by:
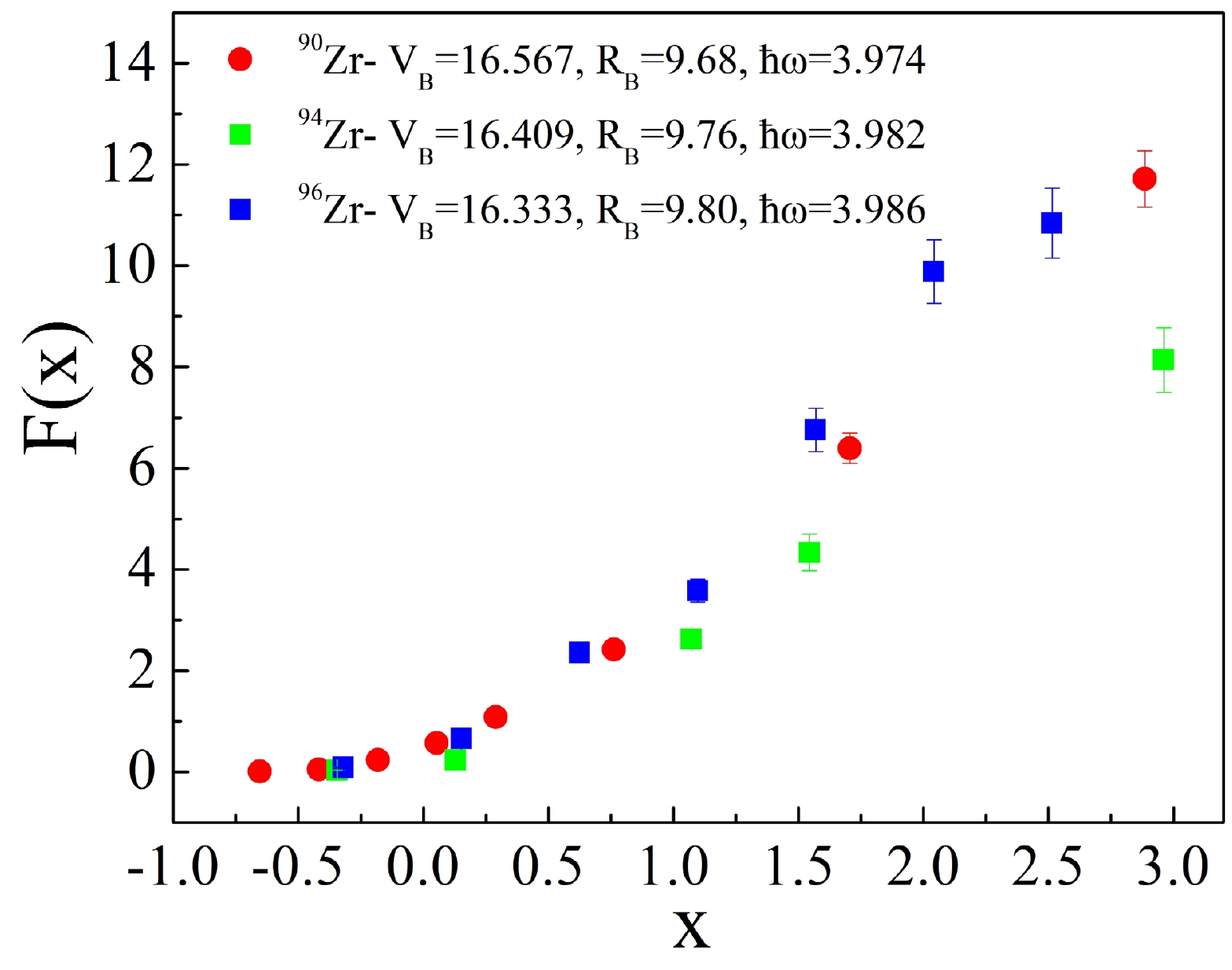
Figure 4. (color online) Systematic comparison of reduced CF cross sections between 6Li + 90, 94, 96Zr systems.
$ F(x) =\frac{2E_{\rm c.m.}}{ R_B^2\hbar\omega}\sigma_{\rm fus}, $

(2) $ x =\frac{E_{\rm c.m.}-V_B}{\hbar\omega}, $

(3) where
$ V_B $ ,$ R_B $ , and$ \hbar\omega $ denote the barrier height, radius, and the curvature of the Coulomb barrier, respectively. Specifically, the data on 6Li + 90, 96Zr systems are considered from Refs. [11, 29]. All the optical barrier parameters for each system are calculated from São Paulo potential (SPP) [30]. The reduced CF cross sections of 6Li + 90, 94, 96Zr are shown in Fig. 4 with their respective parameters. It can be shown that on 90, 96Zr target the behaviours are quite similar, but a significant lowering down effect has been clearly observed for 94Zr case. However, it is quite difficult to directly obtain the conclusion that it is easier for 6Li to breakup before fusing with 94Zr even if the ICF cross section is larger. This is due to the fact that there could be some other possible reasons. For instance, if the proton transfer reaction of 6Li beam on 94Zr target is enhanced due to some unknown reasons, the measured ICF cross section can also become larger in this case. It is not surprising that the reduced CF cross section for 94Zr case can match with the other two if the used optical parameters are slightly changed, such as increasing the$ V_B $ and decreasing the$ R_B $ and$ \hbar\omega $ . This can be related with the enhancement of the breakup effect. This may imply that the different breakup effects of 94Zr cause changes in the barrier distribution. However, to achieve a self-consistent explanation for the entire systematic check, a more detailed or even microscopic theoretical model is highly needed, one that can account for the minor differences between Zr isotopes and their contributions to the fusion process. This is certainly beyond the scope of the current paper.Before ending the discussion of the current fusion reaction, we want to emphasize that a similar systematic study is also performed for fusion of 32S on 90, 94, 96Zr targets in Ref. [31]. The largest deviation, between the fusion cross sections from the experiment and coupled channel calculation considering the effect of different phonon excitations, occurred again for 94Zr case. Thus the sub-barrier fusion enhancement is also most obvious for 32S + 94Zr system. In Ref. [31], a potential reason is attributed to the coupling effect from the positive Q neutron transfer (PQNT). Furthermore, similar studies might be required for the studies of fusion induced by weakly bound nuclei among the above-barrier region.
-
In Ref. [19], the one-neutron stripping cross sections induced by 6Li on the nearby target nuclei 96Zr were measured by the on-line γ method, in which only the statistic of two characteristic γ rays were identified and collected. The theoretical description is much more complicated when compared with the typical (d, p) reaction given that the inner structure of 6Li and coupling effect should be carefully considered. Furthermore, the spectroscopic amplitude is also quite an important factor. To date, there is still no experiment, which can confirm the angular distribution of the emitted 5Li (need the coincident measurement of proton and α), the spectroscopic amplitude for each channel can only be derived from the shell model calculation with constrained model space and effective interaction.
In the current study, to obtain the one-neutron spectroscopic information of the target overlaps, the shell model calculation has been performed within a valence space including π(1
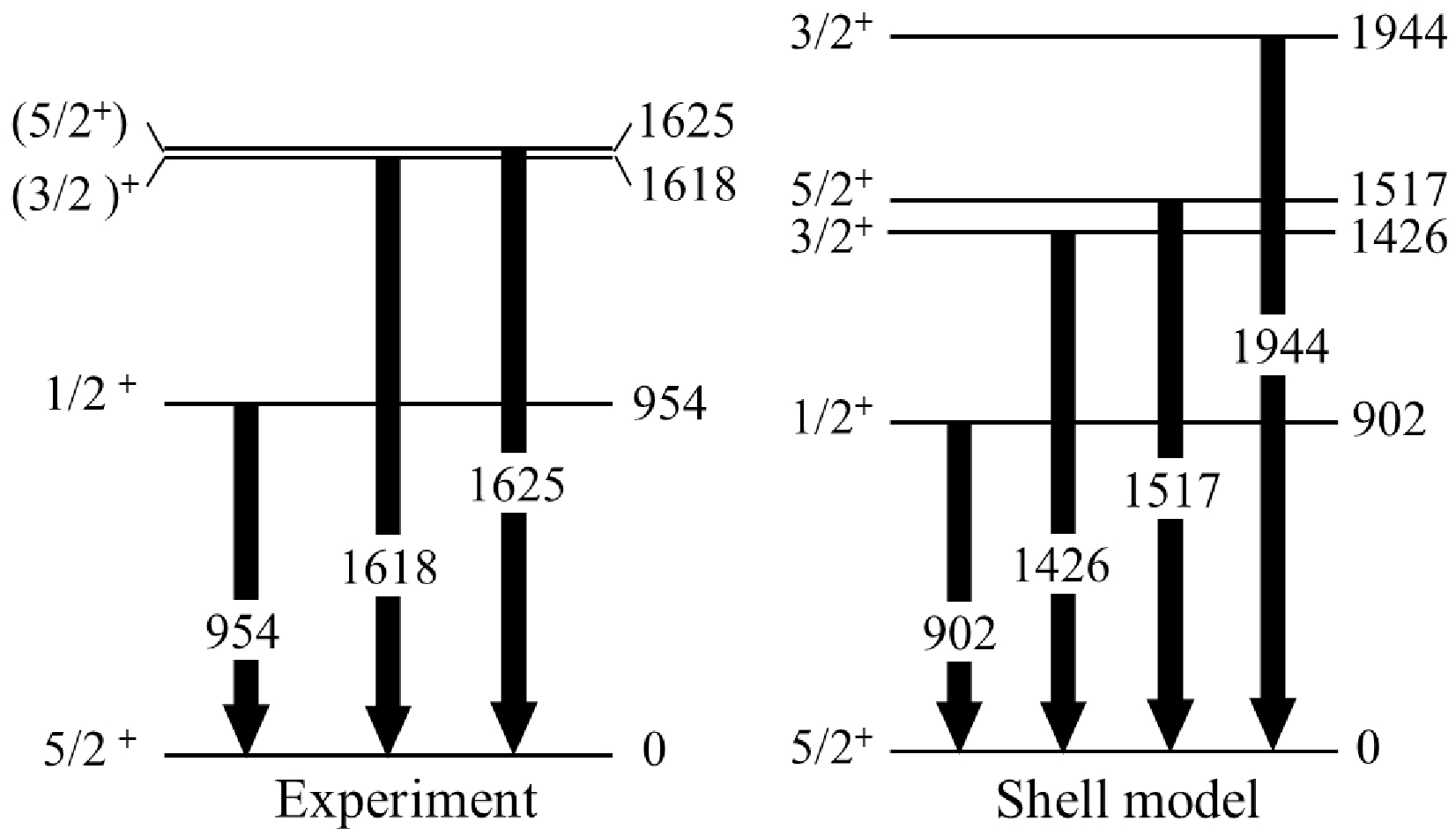
$ f_{5/2} $ , 2$ p_{3/2} $ , 2$ p_{1/2} $ , 1$ g_{9/2} $ ) and ν (1$ f_{5/2} $ , 2$ p_{3/2} $ , 2$ p_{1/2} $ , 1$ g_{9/2} $ , 1$ g_{7/2} $ , 2$ d_{5/2} $ , 2$ d_{3/2} $ , 3$ s_{15/2} $ , 1$ h_{11/2} $ ) orbitals. Given the limitation of computation power, no neutron is allowed to be excited across the N=50 major shell. The nucleon-nucleon interaction in the$ f_{5/2} p_{1/2} p_{3/2} g_{9/2} $ shell applies directly in the JUN45 interaction [32], while the neutron-neutron interaction in the$ g_{7/2} d_{3/2} d_{5/2}s_{1/2} h_{11/2} $ shell and the proton-neutron interaction across the shells are derived from the monopole based universal interaction +M3Y LS [33, 34].Figure 5 compares the experimental observed level scheme in 95Zr with the shell model calculation, showing reasonable agreement with each other. It should be noted that the experimentally observed 1625-keV level in 95Zr is produced quite strongly in the current one-neutron stripping process. On the other hand, the same level is also observed very clearly in the 94Zr (d, p) 95Zr reaction [35]. Even if its spin-parity is still not clear in the adopted value on NNDC [36], this 1625-keV level most likely has a single-particle nature. As shown in Fig. 5, only considering the energy of level, the spin-parity is tentatively assigned to (5/2+) because in the shell model calculation the
$ 5/2^+_2 $ state at 1517 keV is the only remaining level, which cannot be associated to any known experimental levels in this excitation energy region. Furthermore, it should be noted that two 3/2+ levels have been predicted in the current shell model calculation, one at 1426 keV while the other located at 1944 keV. If we only rely on the energy level, the one at 1426 keV should correspond to the experimentally measured (3/2+) level at 1618 keV. However, through the following discussion on the one-neutron stripping cross section, it becomes apparent that the predicted cross section is highly sensitive to the nature of the produced states in 95Zr. This sensitivity raises questions about the current shell model calculations as well.The theoretical calculation for the one-neutron stripping process in 6Li + 94Zr system was obtained by performing the coupled reaction channel (CRC) method using the Fresco code [37]. The São Paulo double folding potential (SPP) is used in both real and imaginary parts (U = (1.0 + iNi)VSP) of the optical potential. Furthermore, Ni denotes the strength coefficient of the imaginary part. The value of Ni = 0.60 was used to account for the loss of flux due to the breakup channel or the coupling to continuum states, as mentioned in Refs. [38, 39]. For the outgoing partition, strength coefficient was also set equal to 0.78. This coefficient was proved to be appropriate for describing the elastic scattering cross section for many systems in a wide energy interval [40]. The single-particle wave functions were derived using Woods-Saxon potentials for the nuclear interactions in the intrinsic Hamiltonian. The depths of the Woods-Saxon potentials were varied to fit the experimental one-neutron binding energies. Furthermore, the reduced radius and diffuseness were set to 1.25 and 0.65 fm, respectively, for both the 6Li projectile and 94Zr target. The collective states (
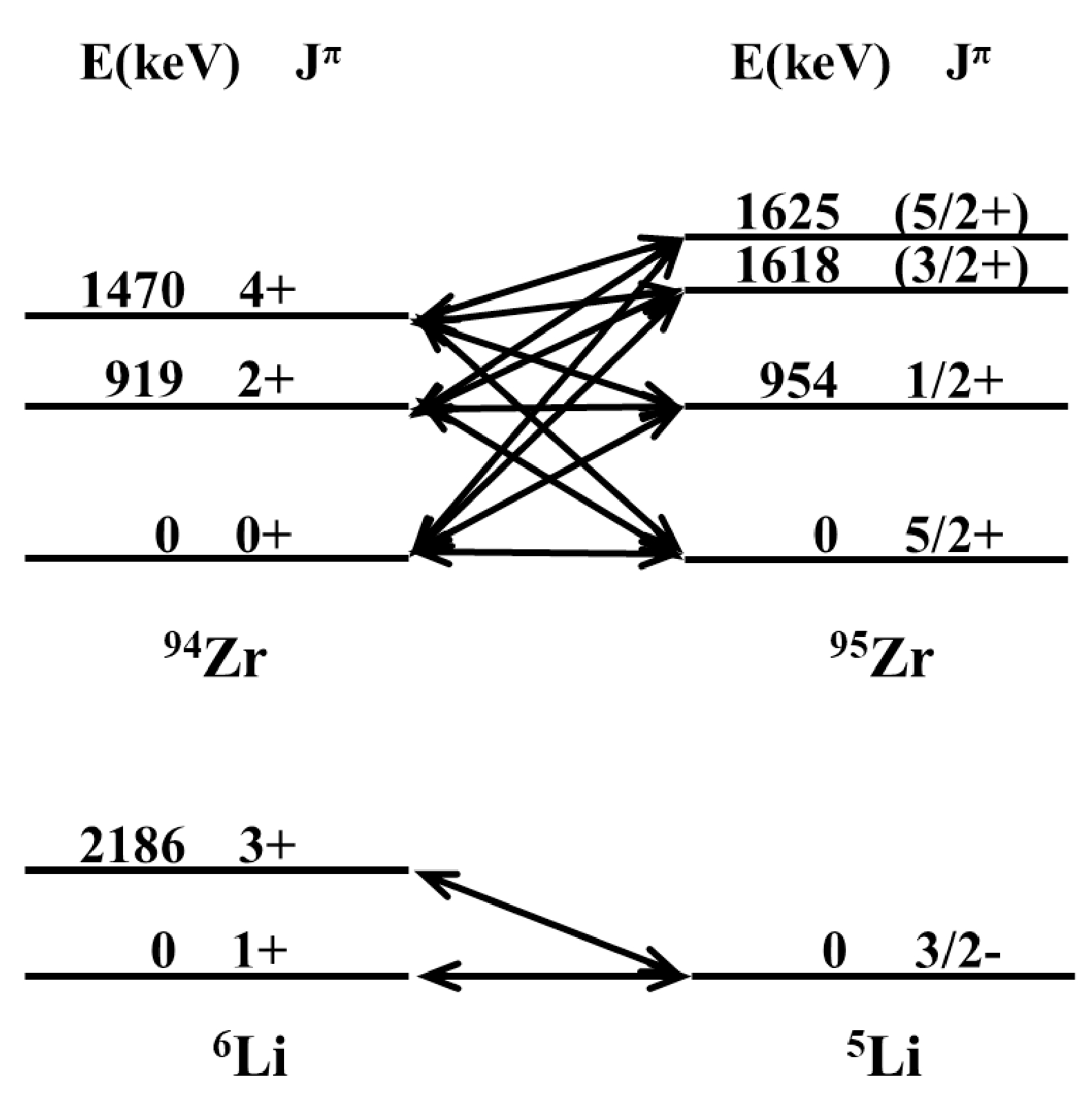
$ 2^+_1 $ and$ 4^+_1 $ ) of the target could be considered in the CRC calculation. Fig. 6 shows the overlap of target and projectile. The spectroscopic amplitudes used in the CRC calculation concerning between 94Zr and 95Zr obtained from the aforementioned shell model calculation are shown in Table 3. For the projectile overlap, the spectroscopic amplitudes for 1+ and 3+ states of 6Li were both set to 1.0.Initial states ν orbital Final states Spec. amp. 94Zr 0+ 2s1/2 95Zr $1/2 ^+_1 $ 

0.9668 1d3/2 95Zr $3/2 ^+_1 $ 

0.1393 1d3/2 95Zr $3/2 ^+_2 $ 

−0.8800 1d5/2 95Zr $5/2 ^+_2 $ 

−0.0910 94Zr $2 ^+_1 $ 

1d5/2 95Zr $1/2 ^+_1 $ 

0.1816 1d3/2 95Zr $1/2 ^+_1 $ 

0.0191 0g7/2 95Zr $3/2 ^+_1 $ 

0.0177 1d5/2 95Zr $3/2 ^+_1 $ 

−0.0127 1d3/2 95Zr $3/2 ^+_1 $ 

−0.1058 2s1/2 95Zr $3/2 ^+_1 $ 

−0.9433 0g7/2 95Zr $3/2 ^+_2 $ 

0.0605 1d5/2 95Zr $3/2 ^+_2 $ 

−0.0980 1d3/2 95Zr $3/2 ^+_2 $ 

0.3673 2s1/2 95Zr $3/2 ^+_2 $ 

−0.1870 0g7/2 95Zr $5/2 ^+_2 $ 

0.0225 1d5/2 95Zr $5/2 ^+_2 $ 

0.1355 1d3/2 95Zr $5/2 ^+_2 $ 

0.0053 2s1/2 95Zr $5/2 ^+_2 $ 

−0.9520 94Zr $4 ^+_1 $ 

0g7/2 95Zr $1/2 ^+_1 $ 

−0.0167 0g7/2 95Zr $3/2 ^+_1 $ 

−0.0145 1d5/2 95Zr $3/2 ^+_1 $ 

−0.0074 2s1/2 95Zr $3/2 ^+_1 $ 

−0.0145 0g7/2 95Zr $3/2 ^+_2 $ 

0.0130 1d5/2 95Zr $3/2 ^+_2 $ 

0.0378 0g7/2 95Zr $5/2 ^+_2 $ 

−0.0276 1d5/2 95Zr $5/2 ^+_2 $ 

−0.1768 1d3/2 95Zr $5/2 ^+_2 $ 

−0.0166 Table 3. Spectroscopic amplitudes for target <94Zr|95Zr> overlap.
In Fig. 7, the CRC calculation is compared with experimental results in the 16–30 MeV beam-energy region. First, it can be observed that, with the change in beam energy, both the calculated and experimental results do not change as rapidly as in the fusion process shown in Fig. 2, showing a similar behaviour with the one-neutron stripping process induced by 6Li on nearby targets such as 96Zr [19] and 89Y [20].
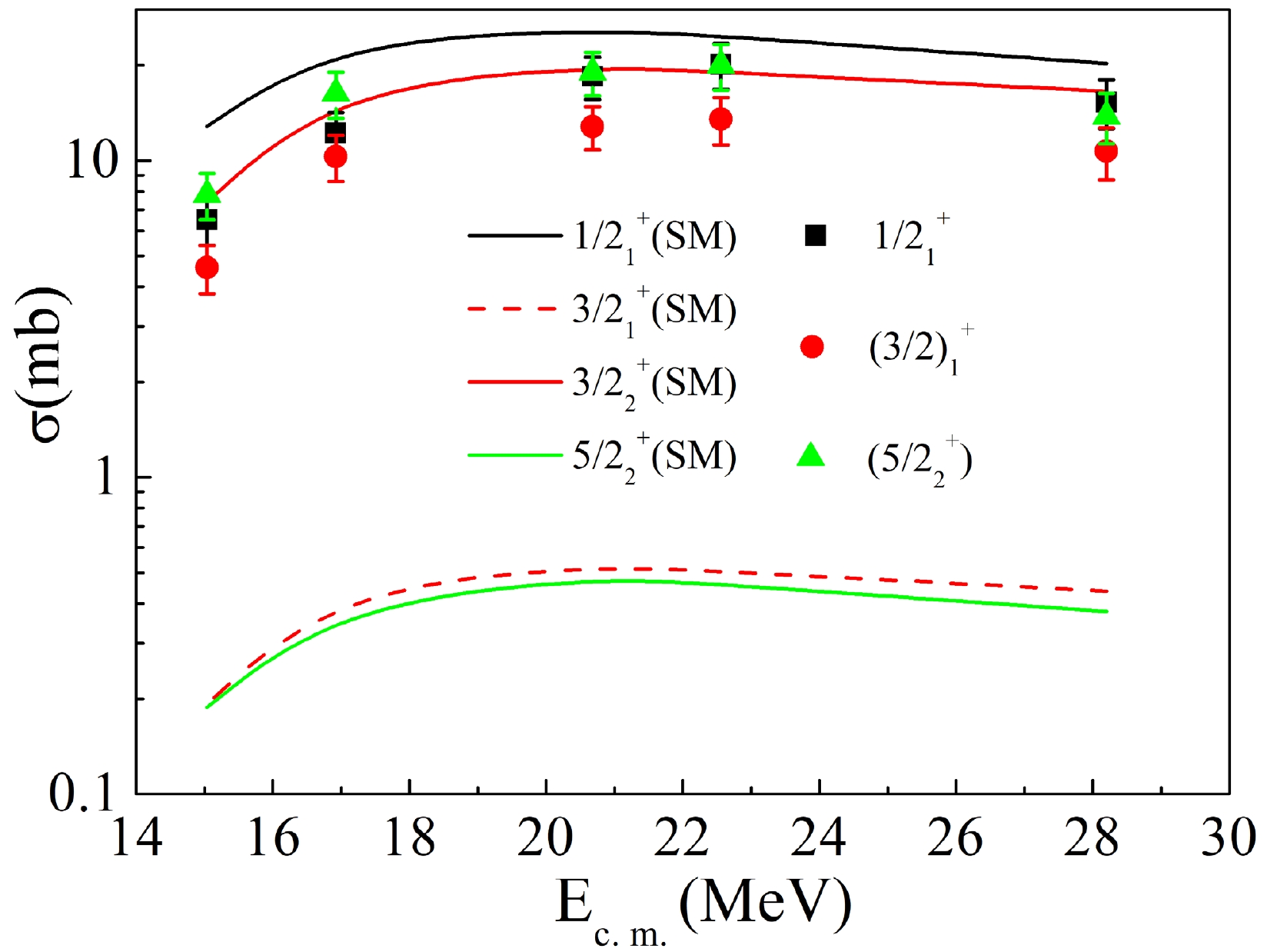
Figure 7. (color online) Comparison of experimental one-neutron stripping cross section with calculations for the 6Li + 94Zr reaction.
Based on the details in Fig. 7, it can be determined that this is the first time the direct production of each level is compared with the CRC calculation, instead of showing a summed one-neutron stripping cross section as in Refs. [18–20, 41]. The new comparison probes not only the reaction mechanism, but also the nature of each observed excited state in 95Zr. In the experimental side, the productions of
$1/2 ^{+}_1 $ ,$(3/2) ^{+}_1 $ , and ($5/2 ^{+}_2 $ ) states are similar to each other among the whole energy region. Meanwhile, from the shell model and CRC calculation, the cross sections of$1/2 ^{+}_1 $ (SM) and$3/2 ^{+}_2 $ (SM) states are orders of magnitude higher than those of$3/2 ^{+}_1 $ (SM) and$5/2 ^{+}_2 $ (SM). This is also consistent with the fact that the shell model predicts$1/2 ^{+}_1 $ (SM) and$3/2 ^{+}_2 $ (SM) states, which are single-particle nature in 95Zr, i.e., ν(s1/2) and ν(d3/2) coupled with the 94Zr ground state, respectively. The argument can be found in Table 3, in which the corresponding spectroscopic amplitudes are almost 1 for both cases. Therefore, referring back to Fig. 5, we suggest that the$3/2 ^{+}_2 $ (SM) state, predicted by shell model calculation, should match the experimental measured (3/2)+ level at 1618 keV. It should be noted that the shell model predicted$3/2 ^{+}_1 $ (SM) state is the coupling between ν(s1/2) and 94Zr 2+ state, which can be observed from the spectroscopic amplitude in Table 3.It is very interesting to continue the discussion on the measured (
$5/2 ^{+}_2 $ ) state whose cross section is comparable to the other two single-particle states at 954 and 1618 keV. This suggests that this is another single-particle state. However, calculation for all the other remaining states fails to reproduce such high cross section. Based on shell model point of view, the remaining possible single-particle states would have the nature of 94Zr 0+ state coupled with ν(g7/2) and ν(d5/2) orbitals. The latter one is the configuration of the ground state of 95Zr, and the former cannot be found in the current shell model calculation with the excitation energy lower than 2 MeV. Thus, the discrepancy between the experiment and theoretical calculation might come from many aspects: (1) In shell model calculation, the interaction as well as the effective single-particle energies should be adjusted or the core-excitation might be required for a better description of the observed level scheme; (2) In the CRC model, the coupling effect is not considered perfectly, especially for the coupling between the excited states and ground state in the target nuclei; (3) In experiment, there are many unknown but weak transitions that feed the 1625-keV level. However, they are not visible in the current analysis, leading to a mismatch in the comparison. Considering the event for the single-particle level at 954 and 1618 keV, there is still an overall overestimation for the cross sections as shown in Fig. 7, leading to a conclusion that further investigation on this topic is highly desired. -
In this study, CF, ICF, TF, and one-neutron stripping cross sections for 6Li + 94Zr system were measured at energies close to the Coulomb barrier by the online γ-ray method. For fusion process, 30% suppression was observed for CF cross section above the Coulomb barrier when compared with the TF. The systematic comparison with CF cross sections of 6Li + 90, 94, 96Zr systems was performed, showing that the breakup of 6Li might differ from 94Zr. For the one-neutron stripping process, the production cross sections of each produced level are extracted and compared with CRC calculation for the first time. The calculations provided similar cross section with the experimental results of 954- and 1618-keV level, but the calculations still overestimate the cross section for 954- and 1618-keV level when compared with experimental results. For the 1625-keV level, the calculations are orders of magnitude higher than the experimental cross section. Thus, the calculations fail to reproduce the cross section of 1625-keV level. According to the comparison, the single-particle nature of the final states can be investigated. Additionally, further study is required to clarify the full reaction mechanism of one-neutron stripping process induced by 6Li.
-
The authors are grateful to the crew of the HI-13 tandem accelerator at the China Institute of Atomic Energy for steady operation of the accelerator and Nuclear Astrophysics Group of China Institute of Atomic Energy who provided the 6Li ion source for us.
Fusion and one-neutron stripping process for 6Li + 94Zr system around the Coulomb Barrier
- Received Date: 2024-02-29
- Available Online: 2024-09-15
Abstract: The complete and incomplete fusion cross section as well as one-neutron stripping process of 6Li + 94Zr system were measured at the energies around the Coulomb barrier by online γ-ray method. In addition to a 30% suppression factor when compared with the measured total fusion process, the complete fusion cross section in 6Li + 94Zr system was observed to be significantly lower than those in the nearby 6Li + 90, 96Zr system. The new experimental result implies that the coupling with breakup channel in the 6Li-induced fusion processes can be affected by the inner structure of the target, which is still not clear in any available model calculation. For the one-neutron stripping process, the direct production cross sections for each level in 95Zr were extracted and compared with the coupled reaction channel calculation, offering a unique opportunity to examine the single-particle nature of the produced excited states. Given the fact that an overall overestimation of the production cross section for 954-keV and 1618-keV levels was observed in the comparison, further investigation is highly demanded in order to understand the full reaction mechanism for the one-neutron stripping process induced by 6Li.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: