-
In 1964, Gell-Mann [1] and Zweig [2, 3] independently formulated a quark model using quarks as fundamental constituents. This model provides a more systematic understanding of numerous hadronic systems, suggesting the possible existence of multiquark states beyond the conventional hadrons. In the 1970s, several theories and models emerged to explore these multiquark states [4], including the MIT bag model [5, 6], constituent quark model [7], string model [8, 9], QCD sum rules [10−12] and their variants, and lattice QCD methods [13].
In comparison to conventional hadronic states, our understanding of exotic hadronic states remains relatively limited. After years of experimental searches, the Belle experiment discovered a distinct particle in 2003, X(3872) [14], which markedly differed from traditional hadronic states. In 2015, the LHCb experiment observed structures resembling pentaquark states, namely
$ P_{c}(4380)^{+} $ and$ P_{c}(4450)^{+} $ , in the decay$ \Lambda^{0}_{b} \to J/ \psi pK^{-} $ [15]. In 2019, the$ P_{c}(4450)^{+} $ state was identified as a two-peak structure comprising$ P_c(4440)^{+} $ and$ P_{c}(4457)^{+} $ [16]. In 2021, the LHCb collaboration discovered two tetraquark states,$ Z_{cs}(4000)^{+} $ and$ Z_{cs}(4220)^{+} $ , containing a strange quark in the decay process$ B^{+}\to J/\psi\phi K^{+} $ [17]. Furthermore, observations such as$ P_{cs} $ [18, 19],$ Z_{c}(3900)^{+} $ [20, 21],$ Z_{c}(4430)^{+} $ [22, 23], and others have represented significant advances on multiquark states, particularly regarding their mass spectra and decay behaviors. Since then, several peculiar hadronic states or candidates have been discovered in high-energy physics experiments, making the investigation of exotic hadronic states one of the focal points.Since the experimental confirmation of the doubly charmed baryon
$ \Xi_{cc}^{++} $ [24, 25], theoretical investigations on multiquark states containing two or more heavy quarks were started [26−32]. Other studies explored potential triply-charm molecular pentaquarks such as$ \Xi_{cc}D_{1} $ and$ \Xi_{cc}D_{2}^{\ast} $ [33], and compact pentaquark states with a$ qqQQ\bar{Q} $ configuration (where$ q=n, s $ ;$ Q=c, b $ ) [27]. Motivated by these findings, our research focuses on the configuration of the triply-heavy pentaquark state$ QQQn\bar{n} $ . In this configuration, this state can be perceived as a pentaquark state formed after the creation of$ n\bar{n} $ combined with a$ QQQ $ , as shown in Fig. 1.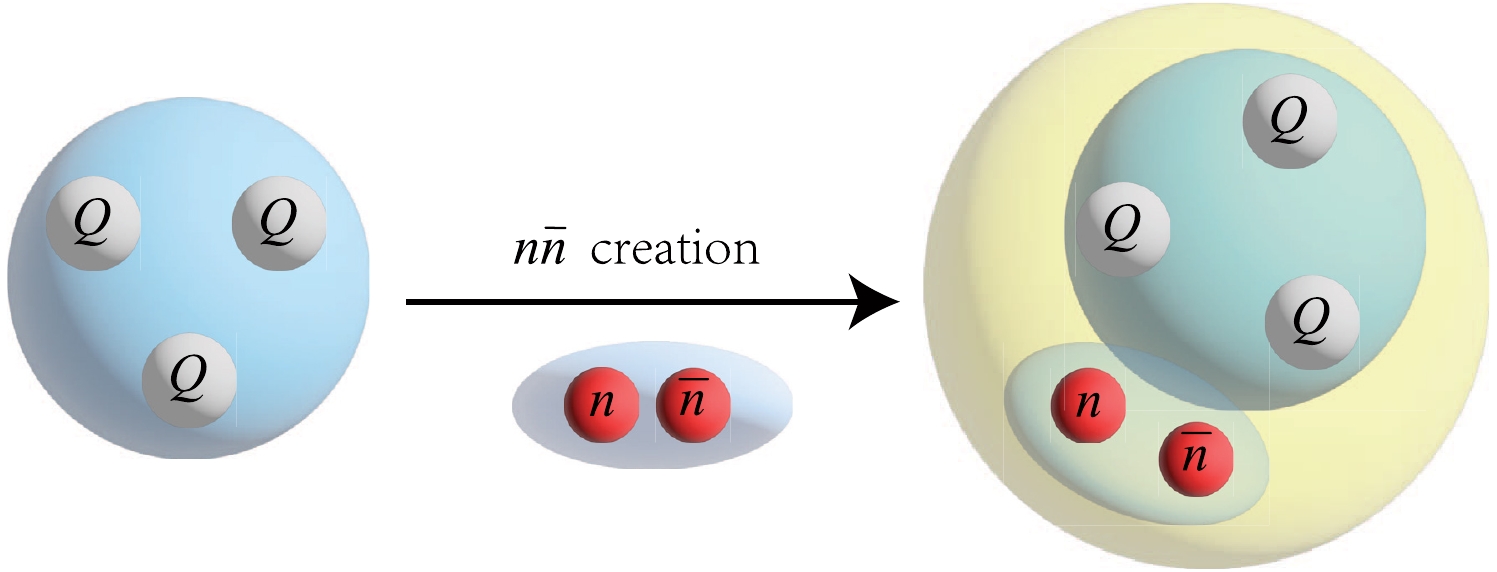
Figure 1. (color online) The triply-heavy baryon
$ QQQ $ combines with the creation of a light-flavored meson$ n\bar{n} $ to form the triply-heavy pentaquark state$ QQQn\bar{n} $ .This study investigated the masses and partial decay width ratios of the triply-heavy pentaquark state
$ QQQn\bar{n} $ , categorized according to the different heavy flavor quarks into$ cccn\bar{n} $ ,$ ccbn\bar{n} $ ,$ bbcn\bar{n} $ , and$ bbbn\bar{n} $ . The MIT bag model has broad applications in baryons [34], mesons [35], pentaquark states, and hybrids [36, 37]. In the framework of the MIT bag model, the masses of$ QQQn\bar{n} $ are calculated by using specific model parameters and fundamental relations. In this paper, based on the partial decay width ratios, we discuss the decay modes of various specific configurations.The structure of this paper is organized as follows. In Section II, we introduce the MIT bag model, which is utilized to calculate the theoretical masses of
$ QQQn\bar{n} $ . Section III outlines the proposed methodology for computing partial decay width ratios; this section contains four subsections presenting the calculated results and decay mode analyses for$ cccn\bar{n} $ ,$ ccbn\bar{n} $ ,$ bbcn\bar{n} $ , and$ bbbn\bar{n} $ , listing the decay products accordingly. Finally, Section IV summarizes this study. -
The MIT bag model describes hadrons as a fundamental physical representation of valence quarks confined within a spherical ''bag''. For a hadron described by a bag of radius R, the model provides a mass formula expressed as follows [38, 39]:
$ \begin{align} \begin{aligned} M(R) =\sum_{i}^{}\omega_{i}+\frac{4}{3} \pi R^{3}B-\frac{Z_{0}}{R}+M_{\rm BD}+M_{\rm CMI}, \end{aligned} \end{align} $

(1) $ \omega_{i}=(m_{i}^{2}+\frac{x_{i}^{2}}{R^{2}})^{1/2}. $

(2) The first term in the equation denotes the cumulative relativistic kinetic energy of all valence quarks confined within the bag. For any quark
$ i $ , the relativistic kinetic energy comprises both the mass$ m_{i} $ and momentum$\dfrac{x_{i}}{R}$ . The parameter$ x_{i} $ is related to the bag radius R by the following equation [38, 39]:$ \tan x_{i}=\frac{x_{i}}{1-m_{i}R-(m_{i}^{2}R^{2}+x_{i}^{2})^{1/2}}. $

(3) This equation is obtained by applying bag surface boundary conditions to the following doublet spinor wave function within the context of the bag model:
$ \begin{align} \psi_{i}\left(r\right)=N_{i}\begin{pmatrix} j_{0}\left(x_{i}r/R\right)U \\ {\rm i} \dfrac{x_{i}}{\left(\omega _{i}+m_{i}\right)R}j_{1}\left(x_{i}r/R\right)\sigma\cdot\hat{r}U \end{pmatrix} {\rm e}^{-{\rm i}\omega_{i}t}. \end{align} $

(4) The bag radius R is determined using the variational method, whereas
$ x_{i} $ is iteratively solved using Eq. (3) [38].The second term is the volume energy, where the constant
$ B $ denotes the energy density difference between perturbative and non-perturbative QCD vacuum. The presence of the third term accounts for zero-point energy, crucial for maintaining the overall stability of the bag.The final two terms in Eq. (1) represent the interaction between quarks. The
$M_{\rm BD}$ term denotes the binding energy within the confinement bag between two heavy quarks or between a heavy quark and a strange quark [40-42]. These binding energies can be expressed in a constant form [35]:$ \begin{align} \begin{Bmatrix} B_{cs}=-0.025\,\mathrm{GeV},& B_{cc}=-0.077\,\mathrm{GeV}, \\ B_{bs}=-0.032\,\mathrm{GeV},& B_{bb}=-0.128\,\mathrm{GeV}, \\ B_{bc}=-0.101\,\mathrm{GeV}. \end{Bmatrix} \end{align} $

(5) The fifth term,
$M_{\rm CMI}$ , is known as chromomagnetic interaction, representing the interaction between quarks confined within the bag by the lowest-order gluon exchange [43]. The chromomagnetic interaction$M_{\rm CMI}$ is expressed as follows [35]:$ \begin{align} \begin{aligned} M_{\rm CMI}=-\sum_{i<j}^{}(\lambda_{i}\cdot \lambda_{j})(\sigma_{i} \cdot \sigma_{j})C_{ij}. \end{aligned} \end{align} $

(6) In the context of the chromomagnetic interaction formula, the subscripts i and j represent indices for quarks or antiquarks, λ denotes the Gell-Mann matrices, σ denotes the Pauli matrices, and
$ C_{ij} $ represents the coupling parameters. For the color and spin factors within the chromomagnetic interaction formula, we employ the following matrix element formula:$ \begin{align} \begin{aligned} \langle\lambda_{i}\cdot\lambda_{j}\rangle_{nm}= \sum_{\alpha=1}^{8}\mathrm{Tr}(c_{in}^{\dagger}\lambda^{\alpha}c_{im}) \mathrm{Tr}(c_{jn}^{\dagger}\lambda^{\alpha}c_{jm}), \end{aligned} \end{align} $

(7) $ \begin{align} \begin{aligned} \langle\sigma_{i}\cdot\sigma_{j}\rangle_{xy}=\sum_{\alpha=1}^{3} \mathrm{Tr}(\chi _{ix}^{\dagger}\sigma ^{\alpha}\chi_{iy})\mathrm{Tr}(\chi _{jx}^{\dagger}\sigma^{\alpha}\chi _{jy}). \end{aligned} \end{align} $

(8) The subscripts n and m in Eq. (7) and x, y in Eq. (8) represent the fundamental vector components of the color and spin wave functions for hadrons, with c and χ symbolizing the color and spin vector bases relevant to quarks. Once the color-spin wave functions are established, the matrices for these two factors can be calculated using the above equations.
Concerning the parameter Cij in the chromomagnetic interaction MCMI, the following relation is satisfied [38]:
$ \begin{align} \begin{aligned} C_{ij}=3\frac{\alpha_{s}(R)}{R^{3}}\bar{\mu}_{i}\bar{\mu}_{j}I_{ij}. \end{aligned} \end{align} $

(9) In the mass formula of the MIT bag model (Eq. (1)), all parameters except for R and xi are constants. The parameters are represented as follows: Z0, which denotes the ground-state energy constant; B, which represents the bag constant; and mi, which denotes the mass of the quark species i or its respective antiquark [35]:
$ \begin{align} \begin{Bmatrix} Z_{0}=1.83, & B^{1/4}=0.145\,\;\mathrm{GeV}, \\ m_{n}=0\,\;\mathrm{GeV}, & m_{s}=0.279\,\;\mathrm{GeV}, \\ m_{c}=1.641\,\;\mathrm{GeV},& m_{b}=5.093\,\;\mathrm{GeV}. \end{Bmatrix} \end{align} $

(10) Given that we do not consider the isospin effects (both cases of
$ m_{n=u,d}=0 $ ), the masses for the isoscalar and isovector$ QQQn\bar{n} $ pentaquarks are degenerate. When we mention a state, we mean all isospin multiplets of this state and assume the readers assign its isospin themselves. By utilizing the given parameters, we limit the variables to only two components: R and$ x_{i} $ . The parameter xi in momentum represents a solution to a transcendental equation, serving as an intermediary reliant on the variable R. Initially, an estimated value for xi is applied to Eq. (3) to solve for R. One can then apply, for a given wave function composed of spatial and color-spin parts, the variational method to Eqs. (1) and (3) to interatively solve for R and xi consistently and thereby compute the masses of triply-heavy pentaquarks [28, 35]. -
Using the MIT bag model described in the previous section, the mass of the studied triply-heavy pentaquark state can be calculated. With the initial mass, one can further research the process of decay. Before starting the study of the triply-heavy pentaquark state decay, certain scattering states need to be eliminated. To differentiate these scattering states from other compact pentaquark states, it is necessary to employ the color-spin wave functions corresponding to each eigenvector of the triply-heavy pentaquark state.
The color-spin wave functions of the triply-heavy pentaquark state resulting from the coupling of baryonic and mesonic decay products can be studied in two different manners: coupling between the baryon color singlet and meson color singlet, denoted as
$ 1_{c} $ , and coupling between the baryon color octet and meson color octet, denoted as$ 8_{c} $ . The color wave functions corresponding to these two coupling modes for the triply-heavy pentaquark states are provided in the appendix [44].$ \begin{align} \Psi=c_{1}|q_{1}q_{2}q_{3}\rangle^{1}_{S_{1}} |q_{4}\bar{q}_{5}\rangle^{1}_{S_{2}}+ c_{2}|q_{1}q_{2}q_{3}\rangle^{8}_{S_{3}} |q_{4}\bar{q}_{5}\rangle^{8}_{S_{4}}+\cdots \end{align} $

(11) For the color-spin wave function structure with the coefficient
$ 1_{c} $ in the above equation, the coupling of S-wave baryon and meson via scattering state may produce a baryon with spin S1 and a meson with spin S2 . If the pentaquark has a strong coupling with$ 1_{c} $ , then the probability associated with this specific vector$ \left |c_{1}\right |^{2} $ tends to a value closer to 1. When the vector satisfies$ \left |c_{1}\right |^{2}\ge0.8 $ , it will be identified as a scattering state. Such states are to be excluded. The compact pentaquark state with the form$ 8_{c} $ can also decay by exchanging quarks to convert$ 8_{c} $ into$ 1_{c} $ .When
$ QQQ\otimes n\bar{n} $ exchanges quarks, we can identify the compact states in the$ QQn\otimes Q\bar{n} $ configuration according to the compact pentaquark states found before. Given that the symmetry of the$ QQn\otimes Q\bar{n} $ configuration is not as high as that of the$ QQQ\otimes n\bar{n} $ configuration, it will contain some non-physical states. Therefore, it is necessary to search for compact states under the$ QQQ\otimes n\bar{n} $ configuration. The decay channels of the compact pentaquark state can be further investigated once the scattering state is eliminated.Here, we specifically study the two-body decay mode
$ A\to B+C $ . For two-body decay, the partial width formula for each decay channel corresponding to the eigenvectors is as follows [44−46]:$ \begin{align} \Gamma_{i}=\gamma_{i}\alpha\frac{k^{2L+1}}{m_{A}^{2L}}\cdot\left |c_{i}\right |^{2}, \end{align} $

(12) $ \begin{align} m_{A}=\sqrt{m_{B}^{2}+k^{2}}+\sqrt{m_{C}^{2}+k^{2}}. \end{align} $

(13) In Eq. (12),
$ \Gamma_{i} $ denotes the partial width of the decay channel$ i $ , while$ \gamma_{i} $ represents a quantity determined by the dynamics of the decay process, α denotes the coupling constant, and$ m_{A} $ corresponds to the mass of the initial compact pentaquark state before decay. The coefficient$ c_{i} $ corresponds to the probability amplitude of the wave function calculated by diagonalization of the chromomagnetic interaction matrix and L represents the orbital angular momentum. Given that we focus on ground states, let us set$ L=0 $ . The symbol k represents the momentum of the decay products in the rest frame for the decay system. The momentum k for the decay products can be computed using Eq. (13). Additionally,$ m_{B} $ and$ m_{C} $ represent the masses of the baryon and meson produced in the decay, respectively. The mass parameters of the decay products are primarily sourced from the Particle Data Group [35, 47, 48], while the mass parameters of the triply-heavy baryons are derived from calculations based on the MIT bag model [28].The decay coefficient
$ \gamma_{i} $ for the two-body decay$ A\to B+C $ depends on the spatial wave functions of the initial and final states. For decay channels composed of scalar mesons (or vector mesons) and baryons with specific flavor combinations in the products, the corresponding$ \gamma_{i} $ values are the same. For instance, if particle A undergoes decay, the resulting particle B (a baryonic product) can be either$ B(J=1/2) $ or$ B^{\ast}(J=3/2) $ , while the resulting particle C (a mesonic product) can be either$ C (J=0) $ or$ C^{\ast} (J=1) $ . For each decay channel in this decay process, the relation between the decay coefficients is as follows [44, 49, 50]:$ \begin{align} \gamma_{BC}=\gamma_{BC^{\ast}}=\gamma_{B^{\ast}C}=\gamma_{B^{\ast}C^{\ast}}. \end{align} $

(14) This relation applies to decay processes in which the baryons and mesons in the decay products possess a definite flavor configuration. Note that for the degenerate pentaquarks of isoscalar and isovector, they have the same
$ QQn\otimes Q\bar{n} $ decay modes and relevant partial widths, indicating that the width ratios between the decays with final states having different isospin I are equal. Note also that there are no isospin-dependent interactions in the adopted model for spectrum and width investigations.For a compact pentaquark with a specific
$ J^{P} $ quantum number and mass, when the flavor compositions of the resulting baryons and mesons after decay are given, multiple decay channels can exist. Among these channels, we selected the partial width of one decay channel as a reference standard. Then, we calculated the ratio of the partial widths of the remaining decay channels to that of the selected channel. This allowed us to obtain the partial decay width ratios for all decay channels involving specific flavor combinations of baryons and mesons, along with their corresponding decay products.For the triply-heavy pentaquark states, there exist three possible
$ J^{P} $ quantum numbers:$ 1/2^{-} $ ,$ 3/2^{-} $ , and$ 5/2^{-} $ . In this study, we classified pentaquark states according to each$ J^{P} $ quantum number and flavor configuration, and analyzed them accordingly. The analysis of$ QQQn\bar{n}(Q=b,c) $ in the following four subsections is mainly divided into two aspects: the scattering states, which are distinguished from the compact pentaquark states; and the decay channels and partial decay width ratios of the compact pentaquark states. -
Using the previously described MIT bag model approach and chromomagnetic interaction, we obtained the masses and eigenvectors of the
$ cccn\bar{n} $ type pentaquark states listed in Table 1. Let us first focus on the eigenvectors of the$ cccn\bar{n} $ type pentaquark states. According to the color-spin wave functions provided in the appendix for the$ QQQn\bar{n} $ type, we observe the following feature of the$ J^{P} $ quantum numbers: for$ J^{P}=1/2^{-} $ , only the third coefficient in each eigenvector corresponds to a$ 1_{c} $ state; for$ J^{P}=3/2^{-} $ , both the second and third coefficients in the respective eigenvectors correspond to a$ 1_{c} $ state; and for$ J^{P}=5/2^{-} $ , there is only one coefficient in the eigenvector, which also corresponds to a$ 1_{c} $ state.State $ J^{P} $ 

$ R_0 $ 

Mass Eigenvector Scattering state $ cccn\bar{n} $ 

$ {1/2}^{-} $ 

5.437 5.741 (0.302, 0.499, 0.812) 5.523 5.827 (−0.839, −0.273, 0.471) 5.665 5.963 (0.455, −0.827, 0.330) $ {3/2}^{-} $ 

5.424 5.372 (−0.108, 0, 0.994) $ \Omega_{ccc}\pi $ 

5.555 5.786 (0, 1, 0) $ \Omega_{ccc}\rho/\omega $ 

5.546 5.854 (0.994, 0, 0.106) $ {5/2}^{-} $ 

5.555 5.786 (1) $ \Omega_{ccc}\rho/\omega $ 

Table 1. Masses, bag radius, eigenvectors, and scattering states of the triply-heavy pentaquark state
$ cccn\bar{n} $ system for each$ J^{P} $ quantum number. The unit of mass is GeV whereas the unit of bag radius is$ \mathrm {GeV^{-1}} $ .When the
$ J^{P} $ quantum number is$ 1/2^{-} $ , the square of the coupling coefficient with$ 1_{c} $ in the eigenvector corresponding to the state with a mass of 5.741 GeV is below 0.8. Hence, this state cannot be defined as a scattering state. Similarly, the coefficients coupled to$ 1_{c} $ at 5.827 and 5.963 GeV indicate that they cannot form a scattering state either. In summary, when$ J^{P}=1/2^{-} $ , the states of the$ cccn\bar{n} $ configuration have no scattering states.When
$ J^{P} = 3/2^{-} $ , the square of the coefficients coupled to$ 1_{c} $ in the eigenvectors at 5.372 and 5.786 GeV are greater than 0.8, indicating that both states are scattering states.The case of
$ J^{P}=5/2^{-} $ is of particular interest. Unlike color-spin wave function systems of the triply-heavy pentaquark states with$ J^{P} $ quantum numbers of$ 1/2^{-} $ and$ 3/2^{-} $ , the color-spin wave function system with$ J^{P}=5/2^{-} $ in the$ cccn\bar{n} $ configuration ($ QQQn\bar{n} $ configuration in the appendix) shows that only the scattering state exists. Therefore, the decay of the triply-heavy pentaquark state with respect to$ J^{P}=5/2^{-} $ is no longer discussed in the$ cccn\bar{n} $ configuration.Table 1 lists the decay products corresponding to the scattering states. The missing scattering states correspond to the compact triply-heavy pentaquark states.
After excluding the scattering states, the remaining compact
$ cccn\bar{n} $ pentaquark states exhibit two decay combinations of$ ccc \otimes n\bar{n} $ and$ ccn \otimes c\bar{n} $ , as shown in Fig. 2.
Figure 2. The triply-heavy pentaquark state
$ cccn\bar{n} $ system has two decay combinations: the$ 1_{c} $ state of$ cccn\bar{n} $ decays via$ ccc \otimes n\bar{n} $ , or$ cccn\bar{n} $ transforms through the exchange of quarks into the form$ ccnc\bar{n} $ , which then decays through$ ccn \otimes c\bar{n} $ in its$ 1_{c} $ state.When the
$ J^{P} $ quantum number is$ 1/2^{-} $ , there exist three states with masses of 5.741, 5.827, and 5.963 GeV. In the case of the$ ccc \otimes n\bar{n} $ type decay, the resulting baryon in the$ 1_{c} $ coupling can only be$ \Omega_{ccc} $ of$ J=3/2 $ , and the corresponding meson can be either ρ or ω of$ J=1 $ . For the two possible decay channels, their decay coefficients satisfy the following relation:$ \begin{align} \gamma_{\Omega_{ccc}\omega}=\gamma_{\Omega_{ccc}\rho}=\gamma_{\Omega_{ccc}\pi}. \end{align} $

(15) Using Eqs. (12) and (13), we can obtain the partial decay width of each state on a specific decay channel. By choosing the channel with the largest partial decay width as a reference, we can obtain the partial decay width ratios for the states at 5.741, 5.827, and 5.963 GeV:
$ \begin{align} \begin{aligned} \frac{\Gamma(cccn\bar{n}\longrightarrow \Omega_{ccc}+\omega)}{\Gamma(cccn\bar{n}\longrightarrow \Omega_{ccc}+\rho)} = 0.970, \mathrm{\ at\ }5.741\mathrm{\ GeV}; \\ \frac{\Gamma(cccn\bar{n}\longrightarrow \Omega_{ccc}+\omega)}{\Gamma(cccn\bar{n}\longrightarrow \Omega_{ccc}+\rho)} = 0.983, \mathrm{\ at\ }5.827\mathrm{\ GeV}; \\ \frac{\Gamma(cccn\bar{n}\longrightarrow \Omega_{ccc}+\omega)}{\Gamma(cccn\bar{n}\longrightarrow \Omega_{ccc}+\rho)} = 0.990, \mathrm{\ at\ }5.963\mathrm{\ GeV}. \end{aligned} \end{align} $

(16) Regarding the
$ ccn\otimes c\bar{n} $ type decay, the resulting baryon in the decay includes$ \Xi_{cc}(J=1/2) $ and$ \Xi_{cc}^{\ast}(J=3/2) $ . In addition, the resulting meson also includes two possible particle types, namely$ D $ and$ D^{\ast} $ .When
$ J^{P}=1/2^{-} $ , according to the color-spin wave functions in the$ QQnQ\bar{n} $ section of the appendix, the$ ccc\otimes n\bar{n} $ state coupled with$ 8_{c} $ transforms via quark exchange to the$ ccnc\bar{n} $ state coupled with$ 1_{c} $ . If decay occurs in the form of$ ccn\otimes c\bar{n} $ , there exist three decay channels:$ \Xi_{cc}\otimes D $ ,$ \Xi_{cc}\otimes D^{\ast} $ , and$ \Xi_{cc}^{\ast}\otimes D^{\ast} $ . The momentum$ k $ can be calculated using Eq. (13) based on the masses of$ \Xi_{cc} $ ,$ \Xi_{cc}^{\ast} $ ,$ D $ ,$ D^{\ast} $ , and the$ cccn\bar{n} $ obtained from the MIT bag model.According to the previously defined expression of
$ \gamma_{i} $ , we can obtain the following relation:$ \begin{align} \gamma_{\Xi_{cc} D}=\gamma_{\Xi_{cc} D^{\ast}}=\gamma_{\Xi_{cc}^{\ast} D}=\gamma_{\Xi_{cc}^{\ast} D^{\ast}}. \end{align} $

(17) The obtained decay coefficients
$ \gamma_{i} $ for each decay channel, along with the coefficients of the momentum$ k $ , are inserted into Eq. (12). The partial decay widths for each decay channel can thus be calculated. For each compact pentaquark state, the decay channel with the largest decay width is chosen as the standard. By calculating the partial decay width ratios of other decay channels to the maximum partial decay width, we obtain the partial decay width ratios for each decay channel.For
$ J^{P}=1/2^{-} $ , using the decay width of$ \Xi_{cc}D $ as the standard, the decay width ratios for the pentaquark state with mass of 5.741 GeV are$ \begin{align} \begin{aligned} \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D^{\ast})}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D)} =0.010,\\ \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D^{\ast})}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D)} =0.063. \end{aligned} \end{align} $

(18) For the pentaquark state with 5.827 GeV, using the decay width of
$ \Xi_{cc}D^{\ast} $ as the standard, the partial decay width ratios are$ \begin{align} \begin{aligned} \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D^{\ast})}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D^{\ast})} =0.008,\\ \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D)}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D^{\ast})} =0.055. \end{aligned} \end{align} $

(19) Finally, for the state at 5.963 GeV, using the decay width of
$ \Xi_{cc}^{\ast}D^{\ast} $ as the standard, the partial decay width ratios for each decay channel are$ \begin{align} \begin{aligned} \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D^{\ast})}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D^{\ast})} =0.005,\\ \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D)}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D^{\ast})} =0.033. \end{aligned} \end{align} $

(20) For
$ J^{P}=3/2^{-} $ , the decay channels for the decay$ ccn\otimes c\bar{n} $ include three possible combinations:$ \Xi_{cc}^{\ast}\otimes D $ ,$ \Xi_{cc}\otimes D^{\ast} $ , and$ \Xi_{cc}^{\ast}\otimes D^{\ast} $ . Following the same calculation process, using$ \Xi_{cc}^{\ast}\otimes D^{\ast} $ as the comparative standard, we obtain the following results:$ \begin{align} \begin{aligned} \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}+D^{\ast})}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D^{\ast})} =0.204,\\ \frac{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D)}{\Gamma(cccn\bar{n}\longrightarrow \Xi_{cc}^{\ast}+D^{\ast})} =0.708. \end{aligned} \end{align} $

(21) Table 2 shows the partial decay width ratios of all decay channels for compact pentaquark states with
$ cccn\bar{n} $ structure.$ J^{P} $ 

Mass $ ccc \otimes n\bar{n} $ 

$ ccn\otimes c\bar{n} $ 

$ \Omega_{ccc}\rho $ 

$ \Omega_{ccc}\omega $ 

$ \Omega_{ccc}\pi $ 

$ \Xi_{cc} ^{*}D^{*} $ 

$ \Xi_{cc}^{*} D $ 

$ \Xi_{cc}D ^{*} $ 

$ \Xi_{cc}D $ 

$ {{1/2}^{-}} $ 

5.741 1 0.970 0.010 0.063 1 5.827 1 0.983 0.008 1 0.055 5.963 1 0.990 1 0.005 0.033 $ {{3/2}^{-}} $ 

5.854 0 0 1 1 0.708 0.204 Table 2. Partial decay width ratios for the decays of the pentaquark configurations
$ ccc\otimes n\bar{n} $ and$ ccn\otimes c\bar{n} $ .The unit of mass is GeV.The results in Table 1 shows that for the
$ cccn\bar{n} $ system with$ J^{P}=1/2^{-} $ , none of the three states is a scattering state. When the$ cccn\bar{n} $ system undergoes decay in the$ ccc\otimes n\bar{n} $ manner, the$ J^{P}=1/2^{-} $ decay channels include$ \Omega_{ccc}\omega $ and$ \Omega_{ccc}\rho $ , while the$ J^{P}=3/2^{-} $ decay channel is$ \Omega_{ccc}\pi $ . There is no shared decay channel between these two cases.When decayed in the
$ ccn\otimes c\bar{n} $ configuration, the three states with$ J^{P} $ quantum number$ 1/2^{-} $ have the same decay channels; however, the dominant decay channels are completely different. The dominant decay channels are those in Table 2 with a partial decay width ratio equal to 1.The decay channel
$ \Omega_{ccc}\pi $ in the$ ccc\otimes n\bar{n} $ configuration is forbidden when$ J^{P}=1/2^{-} $ , because it would violate the conservation of angular momentum. If the triply-heavy pentaquark state$ cccn\bar{n} $ were to decay into the$ \Omega_{ccc}\pi $ channel in the$ ccc\otimes n\bar{n} $ configuration, the resulting decay products would generate a mutual orbital angular momentum of$ L=1 $ . While this would satisfy the conservation of angular momentum, the presence of orbital angular momentum would violate parity conservation after decay. Therefore, the$ \Omega_{ccc}\pi $ decay channel is disallowed. The same holds true for other forbidden decay channels. -
Next, we investigate the decay channels present in the structure of the compact pentaquark states with flavor composition
$ ccbn\bar{n} $ . Using the specific color-spin wave functions of the$ QQQn\bar{n} $ type and the obtained eigenvectors, we differentiate between the scattering and compact pentaquark states for$ ccbn\bar{n} $ , as shown in Table 3.$ R_{0}=5.338\,\mathrm{GeV^{-1}} $ 

State $ J^{P} $ 

Mass Eigenvector Scattering state $ ccbn\bar{n} $ 

$ {1/2}^{-} $ 

8.699 (–0.081, –0.004, –0.068, –0.062, –0.001, –0.001, 0.001, 0.993) $ \Omega_{ccb}\pi $ 

9.087 (–0.048, –0.437, –0.312, 0.131, –0.027, –0.575, 0.600, –0.019) 9.109 (–0.079, –0.073, 0.035, 0.074, 0.254, –0.668, -0.686, 0.001) 9.144 (0.153, 0.162, 0.859, –0.084, 0.108, –0.292, 0.323, 0.066) 9.172 (–0.714, 0.088, –0.009, –0.676, 0.050, –0.068, 0.084, –0.100) 9.203 (0.596, 0.134, 0.200, –0.621, –0.373, –0.237, –0.068, –0.004) 9.324 (0.308, –0.309, –0.081, –0.317, 0.810, 0.206, 0.059, –0.001) 9.299 (–0.032, –0.810, 0.335, –0.149, –0.353, 0.187, –0.222, 0.008) $ {3/2}^{-} $ 

8.712 (0.078, –0.041, –0.002, –0.040, 0, –0.995, 0) $ \Omega_{ccb}^{\ast}\pi $ 

9.113 (–0.047, –0.015, 0.151, –0.019, 0.201, –0.003, 0.966) $ \Omega_{ccb}\rho/\omega $ 

9.124 (0.031, 0.009, –0.089, 0.012, –0.971, 0.002, 0.218) $ \Omega_{ccb}^{\ast}\rho/\omega $ 

9.181 (0.715, –0.679, –0.093, –0.093, 0.031, 0.088, 0.031) 9.214 (0.584, 0.653, –0.417, 0.209, 0.086, 0.011, 0.090) 9.253 (–0.165, –0.277, –0.191, 0.925, 0.027, –0.039, 0.030) 9.313 (0.333, 0.184, 0.866, 0.299, –0.084, 0.005, –0.093) $ {5/2}^{-} $ 

9.126 (0, 1) $ \Omega_{ccb}^{\ast}\rho/\omega $ 

9.281 (–1, 0) Table 3. Masses, bag radius, eigenvectors, and scattering states of the triply-heavy pentaquark state
$ ccbn\bar{n} $ system for each$ J^{P} $ quantum number. The unit of mass is GeV.After excluding the scattering states, decay widths of the remaining compact pentaquark states are analyzed. The approach for handling the
$ ccbn\bar{n} $ system is similar to that of the$ cccn\bar{n} $ system. The difference is that the decay channels of the compact pentaquark state$ ccbn\bar{n} $ involves three configurations of$ ccb\otimes n\bar{n} $ ,$ ccn\otimes b\bar{n} $ , and$ cnb\otimes c\bar{n} $ , as shown in Fig. 3.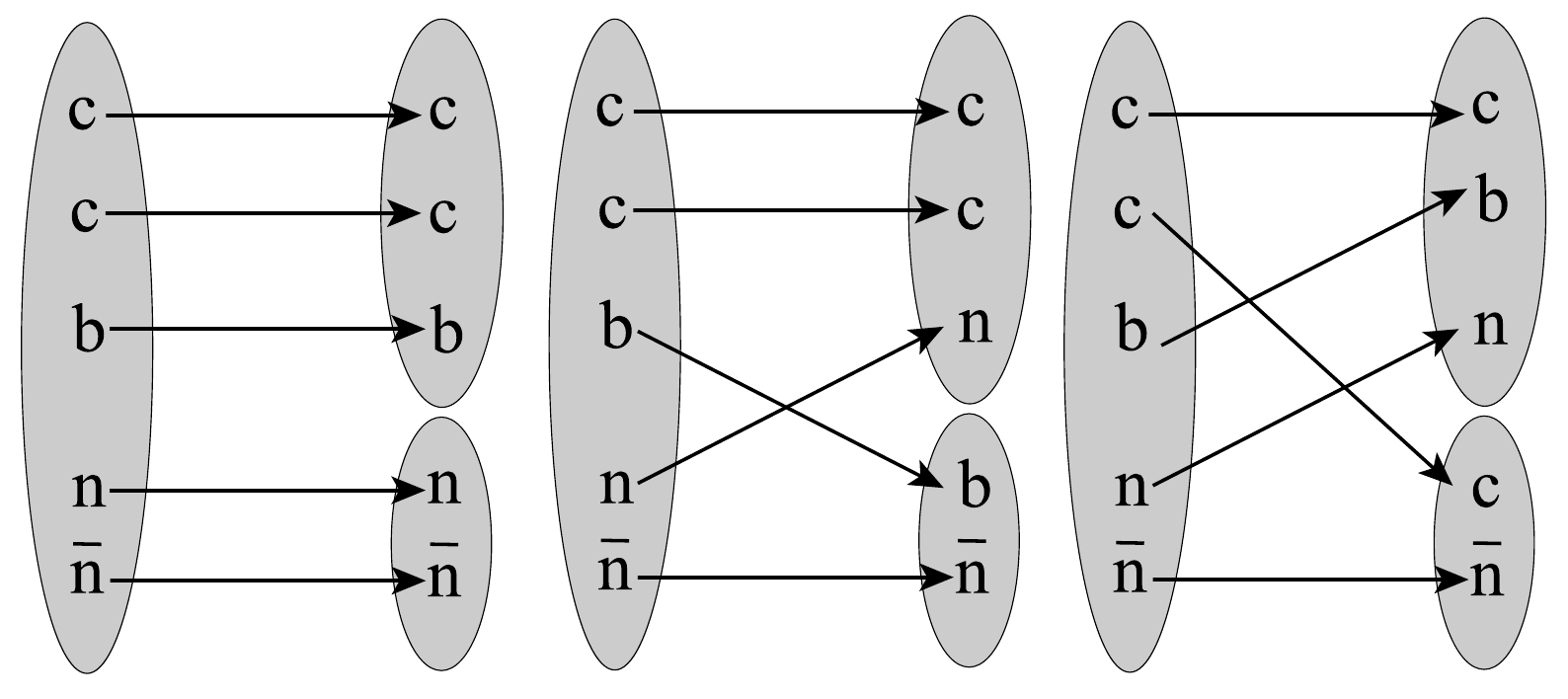
Figure 3. For the triply-heavy pentaquark state
$ ccbn\bar{n} $ , there are three decay combinations: the$ 1_{c} $ state of$ ccbn\bar{n} $ decays via$ ccb \otimes n\bar{n} $ , or$ ccbn\bar{n} $ transforms through the exchange of quarks into the$ 1_{c} $ states of$ ccnb\bar{n} $ and$ cbnc\bar{n} $ , and subsequently decays accordingly.The color-spin wave function of the
$ ccb\otimes n\bar{n} $ type has three$ 1_{c} $ states each for$ J^{P}=1/2^{-} $ and$ J^{P}=3/2^{-} $ . Considering that mesons of the$ n\bar{n} $ configuration include particles ω and ρ with spin 1, then there are six decay channels. If these compact triply-heavy pentaquark states decay into the$ 1_{c} $ state of$ ccb\otimes n\bar{n} $ , the decay coefficients of their six decay channels satisfy the following relation:$ \begin{align} \gamma_{\Omega_{ccb}^{\ast}\omega} = \gamma_{\Omega_{ccb}^{\ast}\rho}= \gamma_{\Omega_{ccb}^{\ast}\pi}= \gamma_{\Omega_{ccb}\omega} = \gamma_{\Omega_{ccb}\rho}= \gamma_{\Omega_{ccb}\pi}. \end{align} $

(22) For the same case, the decay coefficients of decay channels in the
$ ccn\otimes b\bar{n} $ and$ cbn\otimes c\bar{n} $ configurations also satisfy a similar relation:$ \begin{align} \begin{aligned} &\gamma_{\Xi_{cc}^{\ast}B^{\ast}}=\gamma_{\Xi_{cc}B ^{\ast}}=\gamma_{\Xi_{cc}^{\ast}B}=\gamma_{\Xi_{cc}B},\\ \gamma_{\Xi_{bc}^{\ast}D^{\ast}}=&\gamma_{\Xi_{bc}^{'}D ^{\ast}}=\gamma_{\Xi_{bc}D ^{\ast}} =\gamma_{\Xi_{bc}^{'}D}=\gamma_{\Xi_{bc}^{\ast}D}=\gamma_{\Xi_{bc}D}.\\ \end{aligned} \end{align} $

(23) Using Eqs. (12) and (13), we can obtain the partial decay width ratios of the three configurations, as shown in Tables 4 and 5.
$ ccb\otimes n\bar{n} $ 

$ ccn\otimes b\bar{n} $ 

$ J^{P} $ 

Mass $ \Omega_{ccb}^{\ast}\rho $ 

$ \Omega_{ccb}^{\ast}\omega $ 

$ \Omega_{ccb}^{\ast}\pi $ 

$ \Omega_{ccb}\rho $ 

$ \Omega_{ccb}\omega $ 

$ \Omega_{ccb}\pi $ 

$ \Xi_{cc}^{\ast}B^{\ast} $ 

$ \Xi_{cc}^{\ast}B $ 

$ \Xi_{cc}B ^{\ast} $ 

$ \Xi_{cc}B $ 

$ {{1/2}^{-}} $ 

9.087 0.865 0.847 1 0.982 0.002 0.112 0.029 1 9.109 0.897 0.881 1 0.984 0 0.003 0.204 1 9.144 0.776 0.764 1 0.986 0.063 0.027 0.541 1 9.172 0.304 0.300 0.484 0.478 1 0.361 1 0.074 9.203 1 0.988 0.085 0.084 0.004 0.001 1 0.731 9.299 0.685 0.680 1 0.992 0.002 1 0.821 0.005 9.324 1 0.988 0.084 0.083 0 1 0.001 0.054 $ {{3/2}^{-}} $ 

9.181 0.083 0.082 1 0.085 0.084 0.246 0.760 1 9.214 0.870 0.860 0.021 1 0.990 0.002 0.012 1 9.253 0.359 0.355 1 0.439 0.435 0.381 1 0.065 9.313 0.782 0.776 0.003 1 0.993 1 0.218 0.087 $ {{5/2}^{-}} $ 

9.281 1 Table 4. Partial width ratios for the decays of the pentaquark configurations
$ ccb\otimes n\bar{n} $ and$ ccn\otimes b\bar{n} $ . The unit of mass is GeV.$ cbn\otimes c\bar{n} $ 

$ J^{P} $ 

Mass $ \Xi_{bc}^{\ast}D^{\ast} $ 

$ \Xi_{bc}^{\ast}D $ 

$ \Xi_{bc}^{'}D^{\ast} $ 

$ \Xi_{bc}D^{\ast} $ 

$ \Xi_{bc}^{'}D $ 

$ \Xi_{bc}D $ 

$ {{1/2}^{-}} $ 

9.087 0.005 0.010 0.015 1 0.391 9.109 0.017 0.122 0.021 0.899 1 9.144 0.033 0.026 0.262 1 0.019 9.172 0.137 0.201 0.206 0.033 1 9.203 0.010 1 0.031 0.048 0.002 9.299 0.919 0.164 1 0.012 0.070 9.324 1 0.049 0.171 0.054 0.049 $ {{3/2}^{-}} $ 

9.181 0.292 1 0.007 0.245 9.214 0.147 0.035 1 0.618 9.253 0.939 0.046 0.182 1 9.313 1 0.140 0.111 0.374 $ {{5/2}^{-}} $ 

9.281 1 Table 5. Partial width ratios for the decays of the pentaquark configurations
$ cbn\otimes c\bar{n} $ . The unit of mass is GeV.In the states of
$ J^{P}=1/2^{-} $ , the three states with masses of 9.087 GeV, 9.109 GeV, and 9.144 GeV are primarily dominated by the decay channel$ \Omega_{ccb}\rho $ . However, as the mass increases, the dominant decay channel begins to change. The dominant decay of the 9.172 GeV state is the decay channel$ \Omega_{ccb}\pi $ , because the eigenvector of the decay channel$ \Omega_{ccb}\pi $ at 9.172 GeV is larger than the eigenvector of the other decay channels. In addition, the other states are more inclined to$ \rho/\omega $ meson decays.Combined with the result of
$ J^{P}=3/2^{-} $ , we conclude that other decay channels are also possible when the π meson decay channel is dominant. However, when the decay channel of the meson product is$ \rho/\omega $ , almost no decay of the π meson occurs. This indicates that a decay is more likely to occur through channels with higher product mass.For the two configurations of
$ ccn\otimes b\bar{n} $ and$ cbn\otimes c\bar{n} $ , it can be clearly observed that as the mass increases, the product mass of the dominant decay channel also increases slowly, which is reflected in the angular momentum of the decay product. Moreover, the partial decay width ratios of these dominant decay channels are, in most cases, significantly larger than those of other possible decay channels. -
For the
$ bbcn\bar{n} $ system, the coefficients corresponding to the$ 1_{c} $ state in the calculated eigenvectors can differentiate scattering states among states for various$ J^{P} $ quantum numbers, as presented in Table 6.$ R_{0}=5.164\,\mathrm{GeV^{-1}} $ 

State $ J^{P} $ 

Mass Eigenvector Scattering state $ bbcn\bar{n} $ 

$ {1/2}^{-} $ 

12.034 (−0.027, −0.003, −0.097, −0.046, −0.007, 0.001, 0.001, 0.994) $ \Omega_{bbc}\pi $ 

12.443 (0.007, −0.009, −0.254, −0.086, −0.290, 0.602, 0.693, −0.031) 12.453 (−0.032, −0.109, 0.075, 0.039, 0.109, −0.703, 0.688, 0.009) 12.479 (−0.079, −0.101, −0.882, −0.247, −0.150, −0.284, −0.175, −0.101) 12.574 (0.904, 0.256, −0.140, 0.273, −0.122, −0.092, 0.007, 0.023) 12.584 (−0.210, −0.253, −0.256, 0.894, 0.137, 0.089, −0.003, 0.011) 12.647 (−0.053, −0.299, 0.234, 0.122, −0.890, −0.176, −0.121, 0.020) 12.685 (0.358, −0.871, 0.048, −0.197, 0.237, 0.122, −0.029, 0.004) $ {3/2}^{-} $ 

12.047 (0.23, 0.043, 0.004, −0.062, 0, −0.997, 0) $ \Omega_{bbc}^{\ast}\pi $ 

12.446 (−0.018, 0.067, 0.204, −0.066, −0.217, 0.008, 0.950) $ \Omega_{bbc}\rho/\omega $ 

12.462 (−0.008, 0.034, 0.076, −0.032, −0.966, 0.004, −0.242) $ \Omega_{bbc}^{\ast}\rho/\omega $ 

12.503 (−0.088, 0.777, 0.199, −0.568, 0.093, 0.067, −0.118) 12.596 (0.091, −0.611, 0.251, −0.743, 0.035, 0.023, −0.053) 12.619 (0.878, 0.120, −0.430, −0.143, −0.051, 0.033, 0.078) 12.645 (0.461, 0.041, 0.816, 0.311, 0.083, −0.004, −0.128) $ {5/2}^{-} $ 

12.463 (0, 1) $ \Omega_{bbc}^{\ast}\rho/\omega $ 

12.619 (1, 0) Table 6. Masses, bag radius, eigenvectors, and scattering states of the triply-heavy pentaquark state
$ bbcn\bar{n} $ system for each$ J^{P} $ quantum number. The unit of mass is GeV.After excluding the scattering states, for the remaining compact pentaquark states in
$ bbcn\bar{n} $ , there exist three decay configurations:$ bbc\otimes n\bar{n} $ ,$ bbn\otimes c\bar{n} $ , and$ bcn\otimes b\bar{n} $ . The decay coefficients for the different decay channels within these three decay configurations satisfy the following relations:$ \begin{align} \begin{aligned} \gamma_{\Omega_{bbc}^{\ast}\omega}=&\gamma_{\Omega_{bbc}^{\ast}\rho}=\gamma_{\Omega_{bbc}^{\ast}\pi}=\gamma_{\Omega_{bbc}\omega}=\gamma_{\Omega_{bbc}\rho}=\gamma_{\Omega_{bbc}\pi},\\ &\gamma_{\Xi_{bb}^{\ast}D^{\ast}}=\gamma_{\Xi_{bb}D ^{\ast}}=\gamma_{\Xi_{bb}^{\ast}D}=\gamma_{\Xi_{bb}D} ,\\ \gamma_{\Xi_{bc}^{\ast}B^{\ast}}=&\gamma_{\Xi_{bc}^{'}B ^{\ast}}=\gamma_{\Xi_{bc}B^{\ast}} =\gamma_{\Xi_{bc}^{\ast}B}=\gamma_{\Xi_{bc}^{'}B}=\gamma_{\Xi_{bc}B}. \end{aligned} \end{align} $

(24) For each compact pentaquark of a
$ bbcn\bar{n} $ system, the partial decay width of each decay channel can be obtained from Eq. (12). The partial decay channel with the largest decay width is selected for each state in the specific configuration as a reference, thus obtaining the partial decay width ratios for the corresponding decay channel of each state. We list them in Tables 7 and 8.$ bbc\otimes n\bar{n} $ 

$ bbn\otimes c\bar{n} $ 

$ J^{P} $ 

Mass $ \Omega_{bbc}^{\ast}\rho $ 

$ \Omega_{bbc}^{\ast}\omega $ 

$ \Omega_{bbc}^{\ast}\pi $ 

$ \Omega_{bbc}\rho $ 

$ \Omega_{bbc}\omega $ 

$ \Omega_{bbc}\pi $ 

$ \Xi_{bb}^{\ast}D^{\ast} $ 

$ \Xi_{bb}^{\ast}D $ 

$ \Xi_{bb}D ^{\ast} $ 

$ \Xi_{bb}D $ 

$ {{1/2}^{-}} $ 

12.443 0.713 0.704 1 0.988 0.003 0.010 0.034 1 12.453 0.985 0.973 1 0.989 0.0002 0.047 0.909 1 12.479 1 0.989 0.398 0.394 0.185 0.071 0.043 1 12.574 1 0.992 0.006 0.006 0.086 0.615 1 0.120 12.584 1 0.992 0.002 0.002 0.020 0.051 1 0.012 12.647 1 0.993 0.493 0.490 0.016 1 0.090 0.039 12.685 1 0.994 0.058 0.057 0.001 1 0.113 0.075 $ {{3/2}^{-}} $ 

12.503 0.583 0.578 0.430 1 0.991 0.022 1 0.085 12.596 0.425 0.422 0.233 1 0.993 0.300 1 0.030 12.619 0.416 0.413 0.217 1 0.993 1 0.656 0.009 12.645 0.409 0.407 0.012 1 0.994 1 0.204 0.085 $ {{5/2}^{-}} $ 

12.619 1 Table 7. Partial width ratios for the decays of the pentaquark configurations
$ bbc\otimes n\bar{n} $ and$ bbn\otimes c\bar{n} $ . The unit of mass is GeV.$ bcn\otimes b\bar{n} $ 

$ J^{P} $ 

Mass $ \Xi_{bc}^{\ast}B^{\ast} $ 

$ \Xi_{bc}^{\ast}B $ 

$ \Xi_{bc}^{'}B^{\ast} $ 

$ \Xi_{bc}B^{\ast} $ 

$ \Xi_{bc}^{'}B $ 

$ \Xi_{bc}B $ 

$ {{1/2}^{-}} $ 

12.443 0.066 0.139 0.018 0.103 1 12.453 0.028 0.043 0.170 1 0.538 12.479 0.087 0.342 0.254 1 0.058 12.574 0.013 1 0.287 0.115 0.530 12.584 0.006 1 0.112 0.870 0.821 12.647 0 0.022 1 0.004 0.330 12.685 1 0.002 0.084 0.084 0.075 $ {{3/2}^{-}} $ 

12.503 0.372 0.671 0.628 1 12.596 0.518 0.783 0.435 1 12.619 0.618 1 0.628 0.575 12.645 1 0.021 0.045 0.422 $ {{5/2}^{-}} $ 

12.619 1 Table 8. Partial width ratios for the decays of the pentaquark configurations
$ bcn\otimes b\bar{n} $ . The unit of mass is GeV.The structures of the
$ bbcn\bar{n} $ and$ ccbn\bar{n} $ systems are similar. Given that the masses of the$ bbcn\bar{n} $ system are larger, they are more likely to decay. Therefore, as the mass of the$ bbcn\bar{n} $ system increases, the characteristics of the decay channels become more evident.When the
$ bbcn\bar{n} $ system decays through the$ bbc\otimes n\bar{n} $ configuration, the two states at 12.443 GeV and 12.453 GeV and$ J^{P}=1/2^{-} $ , and the partial decay width ratios of the four decay channels$ \Omega_{bbc}^{\ast}\rho $ ,$ \Omega_{bbc}^{\ast}\omega $ ,$ \Omega_{bbc}\rho $ , and$ \Omega_{bbc}\omega $ are all larger. However, the$ bbcn\bar{n} $ system begins to tend to the dominant decay channels$ \Omega_{bbc}^{\ast}\rho $ and$ \Omega_{bbc}^{\ast}\omega $ as the mass increases. When$ J^{P}=3/2^{-} $ , the two decay channels$ \Omega_{bbc}\rho $ and$ \Omega_{bbc}\omega $ always dominate.When the
$ bbcn\bar{n} $ system decays in two configurations of$ bbn\otimes c\bar{n} $ and$ bcn\otimes b\bar{n} $ , it becomes evident that the decay channel tends to increase the decay product mass with the increase of mass. Tables 7 and 8 show that the angular momentum of the decay products increases. -
Finally, concerning the
$ bbbn\bar{n} $ system, similar to the earlier$ cccn\bar{n} $ system, after excluding the scattering states using the calculated eigenvectors, we obtain the values listed in Table 9.State $ J^{P} $ 

$ R_0 $ 

Mass Eigenvector Scattering state $ bbbn\bar{n} $ 

$ {1/2}^{-} $ 

5.032 16.032 (0.357, −0.928, 0.111) 4.940 15.957 (−0.933, −0.355, 0.064) 4.996 15.792 (0.018, 0.126, 0.992) $ \Omega_{bbb}\rho/\omega $ 

$ {3/2}^{-} $ 

5.011 15.796 (0, 1, 0) $ \Omega_{bbb}\rho/\omega $ 

4.972 15.967 (0.999, 0, 0.034) 4.846 15.377 (−0.035, 0, 0.999) $ \Omega_{bbb}\pi $ 

$ {5/2}^{-} $ 

5.011 15.796 (1) $ \Omega_{bbb}\rho/\omega $ 

Table 9. Masses, bag radius, eigenvectors, and scattering states of the triply-heavy pentaquark state
$ bbbn\bar{n} $ system for each$ J^{P} $ quantum number. The unit of mass is GeV whereas the unit of bag radius is$ \mathrm{ GeV^{-1} } $ .The compact pentaquark states
$ bbbn\bar{n} $ have two decay configurations:$ bbb\otimes n\bar{n} $ and$ bbn\otimes b\bar{n} $ . The decay coefficients for different decay channels satisfy the following relations:$ \begin{align} \begin{aligned} &\gamma_{\Omega_{bbb}\omega}=\gamma_{\Omega_{bbb}\rho}=\gamma_{\Omega_{bbb}\pi},\\ &\gamma_{\Xi_{bb}^{\ast}B^{\ast}}=\gamma_{\Xi_{bb}^{\ast}B}=\gamma_{\Xi_{bb}B^{\ast}}=\gamma_{\Xi_{bb}B}. \end{aligned} \end{align} $

(25) Using the same computational method, the decay partial width ratio for each decay channel of
$ bbbn\bar{n} $ are listed in Table 10.$ bbb\otimes n\bar{n} $ 

$ bbn\otimes b\bar{n} $ 

$ J^{P} $ 

Mass $ \Omega_{bbb}\rho $ 

$ \Omega_{bbb}\omega $ 

$ \Omega_{bbb}\pi $ 

$ \Xi_{bb}^{\ast}B^{\ast} $ 

$ \Xi_{bb}^{\ast}B $ 

$ \Xi_{bb}B^{\ast} $ 

$ \Xi_{bb}B $ 

$ {{1/2}^{-}} $ 

15.957 1 0.995 0.023 1 0.236 16.032 1 0.995 1 0 0.124 $ {{3/2}^{-}} $ 

15.967 0 0 1 1 0.608 0.198 Table 10. Partial width ratios for the decays of the pentaquark configurations
$ bbb\otimes n\bar{n} $ and$ bbn\otimes b\bar{n} $ . The unit of mass is GeV.In the decay process of the
$ bbb\otimes n\bar{n} $ configuration, there are distinct decay channels for each$ J^{P} $ quantum number. However, in the$ bbn\otimes b\bar{n} $ configuration, the angular momentum of decay products increases with the increase of mass of decay channels dominated by different states. -
This study comprehensively investigated the properties of the triply-heavy pentaquark state
$ QQQn\bar{n} $ within the framework of the MIT bag model. We provide a detailed characterization of the mass ranges for different systems of$ QQQ n\bar{n} $ . In this process, we observed that for the$ cccn\bar{n} $ system, the mass range is approximately 5.7−6.0 GeV, while the$ ccbn\bar{n} $ system has a mass range of 9.1−9.3 GeV. The mass for the$ bbcn\bar{n} $ system is within the range of 12.4−12.7 GeV, and the$ bbbn\bar{n} $ system has a mass of approximately 16.0 GeV. Given that the masses of the triply-heavy pentaquarks calculated in this study are all above their respective baryon-meson thresholds, all these pentaquarks are unstable in the two-body strong decay.In addition to mass, we also systematically studied the partial decay width ratios of decay channels for different configurations in each
$ QQQn\bar{n} $ system. Given that the angular momentum is conserved during decay, this limits some types of decay channels. If there is an orbital angular momentum$ L=1 $ between the two particles produced by the decay, then conservation of angular momentum can be satisfied. However, the parity will have an additional –1 related to the orbital angular momentum, resulting in non-conservation of parity for the entire decay process. Therefore, some decay channels are prohibited.After excluding the scattering states, we found that as the mass of each configuration of the triply-heavy pentaquark state increases, and the dominant decay channels (i.e., the decay channels with the partial decay width ratio equal to 1 in each state) tend to the states with the increase in angular momentum of the decay products. The partial decay width ratio of the final dominant decay channels will be much larger than that of other decay channels. This suggests that once the momentum required for decay is satisfied, the residual mass will be as large as possible in the form of decay products.
We hope that these conclusions can be verified in future experiments on the triply-heavy pentaquark state
$ QQQ n\bar{n} $ . -
$ \begin{aligned}[b] \phi_{1}^{P}=\;&|[(12)^{6}3]^{8}(4\bar{5})^{8} \rangle\\ =\;&\frac{1}{4\sqrt{3}}\Big[2\bigl(rrgb\bar{r}+ggbr\bar{g}+bbrg\bar{b}-rrbg\bar{r}-bbgr\bar{b}\\ &-ggrb\bar{g}\bigr)+\bigl(rgbr\bar{r}+grbr\bar{r}+gbrg\bar{g}+bgrg\bar{g}+brgb\bar{b}\\ &+rbgb\bar{b}-brgr\bar{r}-rbgr\bar{r}-rgbg\bar{g}-grbg\bar{g}-gbrb\bar{b}\\ &-bgrb\bar{b}+rggb\bar{g}+grgb\bar{g}+gbbr\bar{b}+bgbr\bar{b}+brrg\bar{r}\\ &+rbrg\bar{r}-rgrb\bar{r}-grrb\bar{r}-gbgr\bar{g}-bggr\bar{g}-brbg\bar{b}\\ &-rbbg\bar{b}\bigr)\Big], \end{aligned} $

(A1) $ \begin{aligned}[b] \phi_{2}^{P}=\;&|[(12)^{\bar{3}}3]^{8}(4\bar{5})^{8}\rangle\\ =\;&\frac{1}{12}\Big[3\bigl(rgrb\bar{r}-grrb\bar{r}+rggb\bar{g}-grgb\bar{g}+gbgr\bar{g}\\ &-bggr\bar{g}+gbbr\bar{b}-bgbr\bar{b}+brbg\bar{b}-rbbg\bar{b}\\ &+brrg\bar{r}-rbrg\bar{r}\bigr)+2\bigl(rgbb\bar{b}-grbb\bar{b}+gbrr\bar{r}\\ &-bgrr\bar{r}+brgg\bar{g}-rbgg\bar{g}\bigr)-\bigl(rgbr\bar{r}-grbr\bar{r}\\ &+gbrg\bar{g}-bgrg\bar{g}+brgb\bar{b}-rbgb\bar{b}+rgbg\bar{g}\\ &-grbg\bar{g}+gbrb\bar{b}-bgrb\bar{b}+brgr\bar{r}-rbgr\bar{r}\bigr)\Big], \end{aligned} $

(A2) $ \begin{aligned}[b] \phi_{3}^{P}=\;&|[(12)^{\bar{3}}3]^{1}(4\bar{5})^{1}\rangle\\ =\;&\frac{1}{3\sqrt{2}}\Big[\bigl(grb-rgb+rbg-brg+bgr-gbr\bigr)r\bar{r}\\ &+\bigl(grb-rgb+rbg-brg+bgr-gbr\bigr)g\bar{g}\\ &+\bigl(grb-rgb+rbg-brg+bgr-gbr\bigr)b\bar{b}\Big]. \end{aligned} $

(A3) $ \begin{aligned}[b] \chi_{1}^{P}=\;&|[(12)_{1}3]_{3/2}(4\bar{5})_{1}\rangle_{5/2}, \chi_{2}^{P}=|[(12)_{1}3]_{3/2}(4\bar{5})_{1} \rangle_{3/2},\\ \chi_{3}^{P}=\;&|[(12)_{1}3]_{3/2}(4\bar{5})_{0}\rangle_{3/2}, \chi_{4}^{P}=|[(12)_{1}3]_{1/2}(4\bar{5})_{1} \rangle_{3/2},\\ \chi_{5}^{P}=\;&|[(12)_{0}3]_{1/2} (4\bar{5})_{1}\rangle_{3/2}, \chi_{6}^{P}=|[(12)_{1}3]_{3/2} (4\bar{5})_{1}\rangle_{1/2},\\ \chi_{7}^{P}=\;&|[(12)_{1}3]_{1/2} (4\bar{5})_{1}\rangle_{1/2}, \chi_{8}^{P}=|[(12)_{1}3]_{1/2}(4\bar{5})_{0}\rangle_{1/2},\\ \chi_{9}^{P}=\;&|[(12)_{0}3]_{1/2}(4\bar{5})_{1}\rangle_{1/2}, \chi_{10}^{P}=|[(12)_{0}3]_{1/2} (4\bar{5})_{0}\rangle_{1/2}. \end{aligned} $

(A4) -
A.Wave function of pentaquark
$ QQQn\bar{n} $ (flavor :Q1 = Q2 = Q3)a.
$ J^{P}=5/2^{-}: $ $ \phi_{3}\chi_{1} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{5/2}. $

(B1) b.
$ J^{P}=3/2^{-}: $ $ \begin{aligned}[b] \frac{1}{\sqrt{2}}\big(\phi_{1}\chi_{5}-\phi_{2}\chi_{4}\big)=\;&\frac{1}{\sqrt{2}}\big(| [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{3/2} \\ &-| [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{3/2}\big), \\ \phi_{3}\chi_{2} =\;& | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{3/2}, \\ \phi_{3}\chi_{3} =\;& | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{0} \rangle_{3/2}. \end{aligned} $

(B2) c.
$ J^{P}=1/2^{-}: $ $ \begin{aligned}[b] \frac{1}{\sqrt{2}}\left(\phi_{1}\chi_{9}-\phi_{2}\chi_{7}\right)=\;&\frac{1}{\sqrt{2}}\big(| [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2} \\ &-| [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2}\big), \\ \frac{1}{\sqrt{2}}\left(\phi_{1}\chi_{10}-\phi_{2}\chi_{8}\right)=\;&\frac{1}{\sqrt{2}}\big(| [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2} \\ &-| [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}\big), \\ \phi_{3}\chi_{6} =\;& | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{1/2}. \end{aligned} $

(B3) B. Wave function of pentaquark
$ QQnQ^{\prime}\bar{n} $ (flavor :Q1 = Q2 ≠ Q3)a.
$ J^{P}=5/2^{-}: $ $ \begin{aligned}[b]& \phi_{2}\chi_{1} = | [(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1} \rangle_{5/2}, \\ & \phi_{3}\chi_{1} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{5/2}. \end{aligned} $

(B4) b.
$ J^{P}=3/2^{-}: $ $ \begin{aligned}[b]& \phi_{1}\chi_{5} = | [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{3/2}, \\ & \phi_{2}\chi_{2} = | [(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1} \rangle_{3/2}, \\ & \phi_{2}\chi_{3} = | [(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{0} \rangle_{3/2}, \\ & \phi_{2}\chi_{4} = | [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{3/2}, \\ & \phi_{3}\chi_{2} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{3/2}, \\ & \phi_{3}\chi_{3} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{0} \rangle_{3/2}, \\ & \phi_{3}\chi_{4} = | [(12)^{\bar{3}}_{1}3]^{1}_{1/2} (4\bar{5})^{1}_{1} \rangle_{3/2}. \end{aligned} $

(B5) c.
$ J^{P}=1/2^{-}: $ $ \begin{aligned}[b] &\phi_{1}\chi_{9} \ = | [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{1}\chi_{10} = | [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{2}\chi_{6} \ = | [(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{2}\chi_{7} \ = | [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{2}\chi_{8} \ = | [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{3}\chi_{6} \ = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{1/2}, \\ &\phi_{3}\chi_{7} \ = | [(12)^{\bar{3}}_{1}3]^{1}_{1/2} (4\bar{5})^{1}_{1} \rangle_{1/2}, \\ &\phi_{3}\chi_{8} \ = | [(12)^{\bar{3}}_{1}3]^{1}_{1/2} (4\bar{5})^{1}_{0} \rangle_{1/2}. \end{aligned} $

(B6) C. Wave function of pentaquark
$ QQ^{\prime}nQ\bar{n} $ (flavor :Q1 = Q3 ≠ Q2)a.
$ J^{P}=5/2^{-}: $ $ \begin{aligned}[b]& \phi_{1}\chi_{1}=|[(12)^{6}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1}\rangle_{5/2}, \\ & \phi_{2}\chi_{1}=|[(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1}\rangle_{5/2}, \\ & \phi_{3}\chi_{1}=|[(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1}\rangle_{5/2}. \end{aligned} $

(B7) b.
$ J^{P}=3/2^{-}: $ $ \begin{aligned}[b] & \phi_{2}\chi_{2}=|[(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1}\rangle_{3/2}, \\& \phi_{1}\chi_{2}=|[(12)^{6}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1}\rangle_{3/2}, \end{aligned} $

$ \begin{aligned}[b] & \phi_{1}\chi_{3}=|[(12)^{6}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{0}\rangle_{3/2}, \\& \phi_{1}\chi_{4}=|[(12)^{6}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1}\rangle_{3/2}, \\ & \phi_{1}\chi_{5}=|[(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1}\rangle_{3/2},\\ & \phi_{2}\chi_{3}=|[(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{0}\rangle_{3/2}, \\ & \phi_{2}\chi_{4}=|[(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1}\rangle_{3/2}, \\ & \phi_{2}\chi_{5} = | [(12)^{\bar{3}}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{3/2}, \\ & \phi_{3}\chi_{2} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{3/2}, \\ & \phi_{3}\chi_{3} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{0} \rangle_{3/2}, \\ & \phi_{3}\chi_{4} = | [(12)^{\bar{3}}_{1}3]^{1}_{1/2} (4\bar{5})^{1}_{1} \rangle_{3/2}, \\ & \phi_{3}\chi_{5} = | [(12)^{\bar{3}}_{0}3]^{1}_{1/2} (4\bar{5})^{1}_{1} \rangle_{3/2}. \end{aligned} $

(B8) c.
$ J^{P}=1/2^{-}: $ $ \begin{aligned}[b] &\phi_{1}\chi_{6} = | [(12)^{6}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{1}\chi_{7} = | [(12)^{6}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{1}\chi_{8} = | [(12)^{6}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{1}\chi_{9} = | [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{1}\chi_{10} = | [(12)^{6}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{2}\chi_{6} = | [(12)^{\bar{3}}_{1}3]^{8}_{3/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{2}\chi_{7} = | [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{2}\chi_{8} = | [(12)^{\bar{3}}_{1}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{2}\chi_{9} = | [(12)^{\bar{3}}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{1} \rangle_{1/2}, \\ &\phi_{2}\chi_{10} = | [(12)^{\bar{3}}_{0}3]^{8}_{1/2} (4\bar{5})^{8}_{0} \rangle_{1/2}, \\ &\phi_{3}\chi_{6} = | [(12)^{\bar{3}}_{1}3]^{1}_{3/2} (4\bar{5})^{1}_{1} \rangle_{1/2}, \\ &\phi_{3}\chi_{7} = | [(12)^{\bar{3}}_{1}3]^{1}_{1/2} (4\bar{5})^{1}_{1} \rangle_{1/2}, \\ &\phi_{3}\chi_{8} = | [(12)^{\bar{3}}_{1}3]^{1}_{1/2} (4\bar{5})^{1}_{0} \rangle_{1/2}, \\ &\phi_{3}\chi_{9} = | [(12)^{\bar{3}}_{0}3]^{1}_{1/2} (4\bar{5})^{1}_{1} \rangle_{1/2}, \\ &\phi_{3}\chi_{10} = | [(12)^{\bar{3}}_{0}3]^{1}_{1/2} (4\bar{5})^{1}_{0} \rangle_{1/2}. \end{aligned} $

(B9)
Masses and decays of triply-heavy pentaquarks
- Received Date: 2024-03-21
- Available Online: 2024-10-15
Abstract: In this study, we analyzed masses and decays of triply-heavy pentaquarks






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: