-
High-quality measurements of neutron-induced nuclear reaction data have improved reactor design and the accuracy of fundamental physics research [1]. Most analysis and simulation codes rely on evaluated cross-section data from libraries such as ENDF/B-VIII.0 [2], CENDL-3.2 [3], or JENDL-5 [4]. These databases also rely on high-precision measurement data for assessment and improvement. The neutron total cross-section is an important experimental input for the evaluation of neutron-induced cross-sections. In the fast-neutron energy range, neutron total cross-sections exhibit significant sensitivity to both compound nucleus model and optical model parameters [5]. Therefore, the accuracy of experimental neutron total cross-section data directly influences the improvement of theoretical nuclear model parameters.
Chromium is commonly alloyed with iron and other materials for structural applications in both fission and fusion nuclear facilities. Recently, it has also been proposed as an alternative to zirconium alloy coatings to enhance the oxidation resistance of cladding [6]. Naturally occurring chromium,
$ ^{\mathrm{nat}} $ Cr, consists of three stable isotopes ($ ^{52,53,54} $ Cr) and an extremely long-lived isotope,$ ^{50} $ Cr (half-life$ > $ 1.8 × 10$ ^{17} $ y). These isotopes have proton number$ Z = 24 $ and are close to the neutron shell closure at$N=28 $ . The major isotope$ ^{52} $ Cr has exactly 28 neutrons. Similar to other nuclei in the same mass region, chromium isotopes have low level densities and a propensity for low-lying unnatural parity states. The low level density manifests as non-statistical fluctuations of neutron cross sections at low energies, enhancing the role of neutron capture by the first resonance levels of odd isotopes [7]. It also causes the resonance fluctuations to extend to higher energies (1 MeV), well into the energy range typical of neutron fission spectra. As expected, these fluctuations affect not only the neutron flux but also neutron leakage control in reactors. Therefore, the need for accurate neutron-induced reaction data of$ ^{\mathrm{nat}} $ Cr can be found on the high-priority request list (HPRL) [8].The evaluated data for the chromium isotopes in the ENDF/B-VIII.0 library followed recent measurements [9] and evaluation efforts [10] in support of the U.S. Department of Energy (DOE) Nuclear Criticality Safety Program (NCSP), with particular focus on the resolved resonance region. In the intermediate and high energy region, although a recent study by Pereslavtsev [11] is currently included in the JEFF-3.3 library [12], the ENDF/B-VIII.0 library still relies on work performed in 1997 by Chiba and the data released in the ENDF/B-VI.1 library [13, 14], which was extended to 200 MeV. By comparing the neutron-induced total cross-section data of chromium in the major evaluation nuclear data libraries, several differences were found among the databases, especially in the neutron resonance energy region. In addition, the 41 sets of experimental data included in the EXFOR [15] database also exhibit some discrepancies in this region. No measurement was found covering the energy region of interest for reactor applications in a single experiment with one type of spectrometer. This is not conducive to the evaluation of nuclear reaction data for natural chromium. To this end, high-precision neutron total cross-section data for chromium across the reactor energy range from a single comprehensive measurement are needed as a reference for data re-evaluation.
In this study, the
$ ^{\rm nat} $ Cr neutron total cross-section was obtained on the back-streaming neutron beamline (Back-n [16, 17]) using the Neutron Total Cross Section Spectrometer (NTOX) and the transmission method over a wide neutron energy range (0.3 eV−20 MeV). The measured neutron total cross-sections were compared with data extracted from EXFOR and evaluation libraries. Theoretical calculation of the$^{\rm{nat}} $ Cr neutron total cross-section in the energy range of 1.5 to 20 MeV was then conducted using TALYS-1.96 for comparison and validation. -
The transmission is the fraction of the neutron counting rate through a sample to the rate without a sample [18]. If
$ N_o $ is the number of counts without a sample and$ N_i $ is the number of counts with a sample placed between the neutron source and detector, then the transmission$ T $ at a specific neutron energy ($ E $ ) is given by$ T= \frac{N_i}{N_o}={\rm e}^{-nd\sigma_T} , $

(1) where
$ n $ denotes the number of atoms per unit volume, and$ d $ is the sample thickness. The neutron total cross-section$ \sigma_T $ can then be determined as$ \sigma_T= -\frac{1}{nd}\ln{T} =\frac{1}{nd}\ln{\frac{(M_o-B_o)/P_o}{(M_i-B_i)/P_i}} , $

(2) where
$ M_i $ and$ M_o $ are the signal counts of the beam-on measurement with sample-in and sample-out, respectively,$ B_i $ and$ B_o $ are the background counts of the beam-on measurement with sample-in and sample-out, respectively, and$ P_o $ and$ P_i $ represent the proton beam intensity, which is used for neutron count normalization and is simultaneously monitored by a current transformer. -
The CSNS Back-n has two experimental stations, Experimental Stations 1(ES#1) and 2(ES
$ \# $ 2), which are 55.0 m and 77.0 m from the neutron targeting station, respectively [19, 20]. The experimental layout for this measurement is shown in Fig. 1. The proton beam current was in double-bunch mode, the average proton hitting power was 125 kW, and the experiment was performed for approximately 152 h. ES$ \# $ 1 was used to install the samples to be measured and ES$ \# $ 2 held the NTOX spectrometer. In each pulse, there were two proton bunches approximately 30 ns wide (rms) with a 410 ns interval. The NTOX spectrometer [21, 22] that was used for the measurements was a multi-layer fast fission chamber (FIXM). The sample changer installed in ES$ \# $ 1 can be remotely controlled to change or remove the sample. The multi-layer fast fission chamber was placed in ES$ \# $ 2, which provided the termination signal of the neutron flight.The main structure of the FIXM consisted of high-purity fission cells, front and rear neutron windows, and a drum cavity. Four cells of
$ ^{235} $ U and four cells of$ ^{238} $ U were arranged in the multi-layer fast fission ionization chamber for low-energy and fast-energy neutron detection, respectively. The time resolution of the FIXM was better than 6 ns. The pulses from the eight fission cells were fed into preamplifiers and digitized by a 1 GHz sampling data acquisition system (DAQ). The proton beam trigger signal was fed directly into the DAQ as the starting trigger signal of the system [23]. -
To improve the accuracy of the measurements, neutron scattering due to the thickness of the sample and the uncertainty of the transmission needed to be considered. Therefore, Geant4 simulation was employed to evaluate the appropriate thickness of the natural chromium sample. In this experiment, a 15 mm thick natural chromium sample was used for the transmission measurement. Additional physical parameters of the sample are listed in Table 1. The sample was oriented perpendicular to the neutron beam to reduce experimental uncertainty. The diameter of the
$ ^{\mathrm{nat}} $ Cr sample was 70 mm to cover the neutron beam with a diameter of approximately$ \Phi50 $ at the sample position. The measurement time for the sample-in phase was 102 h, whereas the measurement time for the sample-out phase was approximately 50 h.Sample Purity (%) Diameter/mm Thickness/mm Mass/g Density/(g/cm $ ^{3} $ )

Abundance (%) $ ^{\mathrm{nat}} $ Cr

99.99 70 15 416.5 7.26 4.345( $ ^{50} $ cr)

83.789( $ ^{52} $ cr)

9.501( $ ^{53} $ cr)

2.365( $ ^{54} $ cr)

Table 1. Characteristic parameters of the
$ ^{\mathrm{nat}} $ Cr sample. -
To determine the incident neutron energy, the time-of-flight (TOF) technique is typically used [24]. It determines the neutron energy by measuring the time taken by a neutron to travel over a fixed distance. In the TOF measurement, the incident neutron kinetic energy
$ E_n $ is expressed as Eq. (3).$ E_{n}= m_{n} c^{2}\left[\frac{1}{\sqrt{1- \left(\dfrac{L}{c \cdot {\rm TOF}_{n}}\right)^{2}}}-1\right], $

(3) where
$ m_n $ is the rest mass of the neutron,$ c $ is the speed of light,$ L $ is the neutron flight length, and${\rm TOF}_n$ is the neutron flight time.Spallation neutrons are generated simultaneously with high-intensity γ-rays (hereafter called γ-flash). Because a γ-flash travels at the speed of light, γ-rays arrive at the NTOX spectrometer before neutrons. Consequently, the time difference between the detected γ-flash and the measured neutron signal can be used to ascertain the neutron TOF [25], as shown in Eq. (4).
$ {\rm TOF}_n = T_n-T_{n0}=T_n-(T_{\gamma}-{\rm TOF}_{\gamma}) , $

(4) where
$ T_n $ is the neutron arrival time determined by the fission signal,$ T_{n0} $ is the generation time of neutrons, and$ T_{\gamma} $ is the arrival time of the γ-flash.${\rm TOF}_{\gamma}$ , denoting the flight time of the γ-flash, is defined as the flight length ($ L $ ) divided by the speed of light ($ c $ ).To derive the neutron kinetic energy (
$ E_n $ ) from the TOF differences between the neutron and γ-flash, three resonance peaks of$ ^{235} $ U at energies of 8.774 eV, 12.386 eV, and 19.288 eV were used to determine the flight length. The neutron flight length can be obtained based on the fitting of the relationship between the resonance peak energy and the neutron arrival time$ T_n $ in Eq. (5).$ T_n-T_{\gamma} = \frac{L}{c}\left[ \frac{1}{\sqrt{1-\left( \dfrac{E_n}{m_nc^2}+1\right)^{-2}}}-1\right]. $

(5) Fitting the resonance peak energies of four different
$ ^{235} $ U fission cells with$ T_n $ , the results of their distances from the target source were obtained, as listed in Table 2, and the fitted distances show that these fission fragments conformed to a geometrical design with a spacing of approximately 20 mm. Because$ ^{238} $ U fission cells are not sensitive to low-energy neutrons, the flight distances of four$ ^{238} $ U fission cells were obtained by increasing the 20 mm distance sequentially through the geometrically designed structure of the FIXM [26].Fission $ ^{235} $ U-1

$ ^{235} $ U-2

$ ^{235} $ U-3

$ ^{235} $ U-4

L/m 77.7380 77.7566 77.7768 77.7966 Table 2. Determined neutron flight path of fission cells.
-
A precise assessment of background contributions was vital in this study. The background included electronic noise,
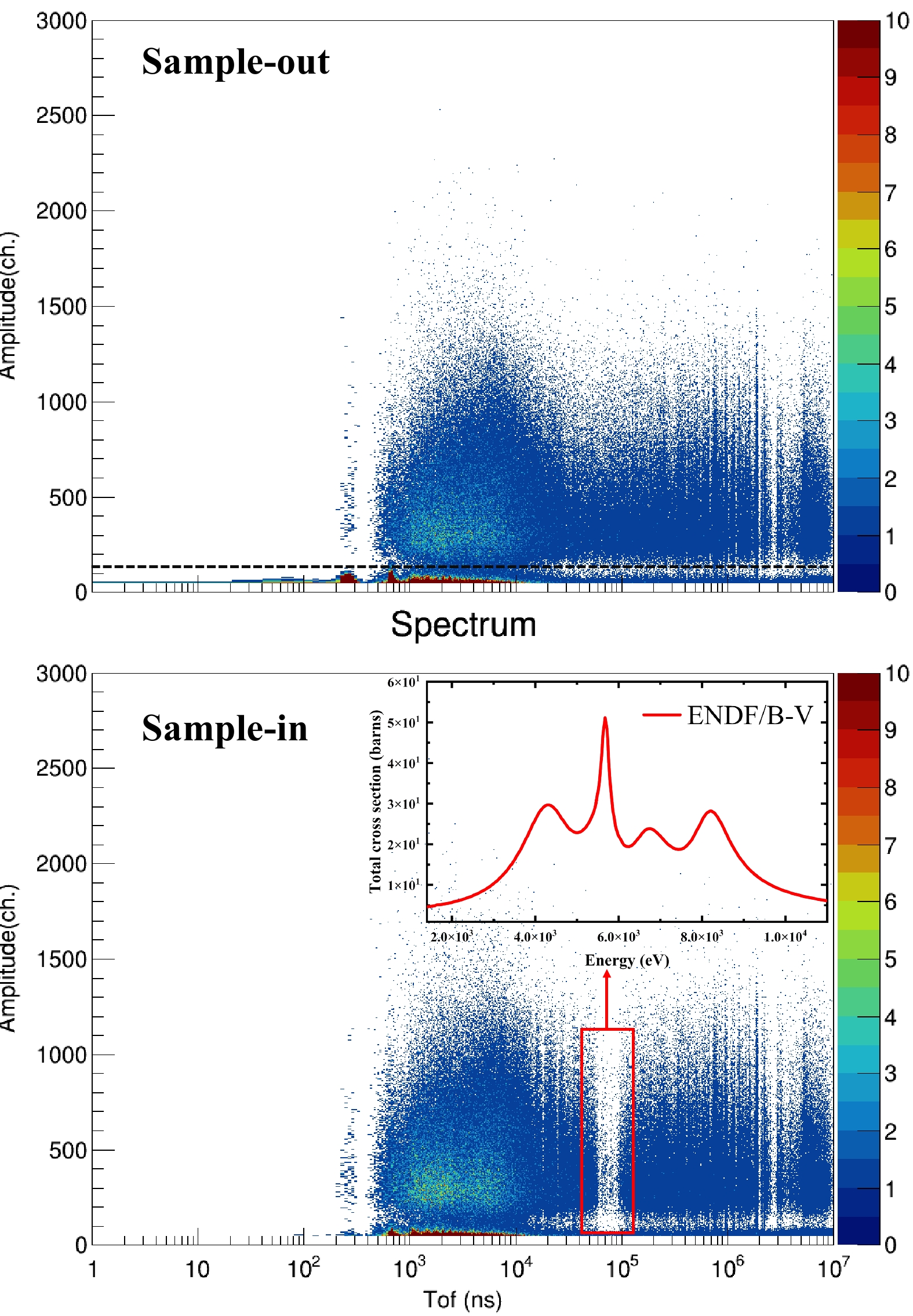
$ \alpha $ -background signals, and environmental neutron background signals.$ \alpha $ -background signals emanate from fission cells and are uniformly distributed over time. More comprehensive insights into this area can be found in a previous paper [27].Signals were obtained from each fission cell time and amplitude statistics, yielding a two-dimensional distribution of TOF versus amplitude. Figure 2 shows the TOF-amplitude two-dimensional distribution of the
$ ^{235} $ U-1 cell with sample-out and sample-in. Leveraging the TOF-amplitude two-dimensional spectrum, background signals were mitigated by implementing distinct amplitude discrimination thresholds. A comparative analysis of the TOF-amplitude two-dimensional sprectrum with sample-out revealed a conspicuous resonance phenomenon within the highlighted red region in the corresponding graph with sample-in. Using the neutron TOF technique, this resonance phenomenon was found to be caused by the presence of significant resonance peaks in the$ ^{\mathrm{nat}} $ Cr total cross-section in the energy range from 2.0×10$ ^3 $ to 1.0×10$ ^4 $ eV. -
In the neutron total cross-section measurement at the CSNS, cadmium foil was used to absorb low-energy neutrons, covering the energy range from the thermal region to hundreds of MeV. The accelerator of the CSNS was operated in the double-bunch mode, where each pulse consists of two proton bunches with a 410 ns interval. This double-bunch effect results in fast neutrons from the second beam bunch simultaneously arriving at the detector with slow neutrons from the first bunch, making them indistinguishable. The 410 ns interval may cause significant uncertainty in the neutron TOF measurement and eventually affect the measurement accuracy of the total cross-section.
Therefore, to reduce the influence of the double-bundle effect and obtain the fission events as a function of neutron energy in the single-bundle mode, the unfolding program DemoUnfolding_v3.4 based on the Bayesian principle was employed. The program correlates measurement data with true data using corresponding matrices and implements unfolding by estimating true data through the Bayesian theorem and iterative algorithms [28]. The energy range of unfolding with
$ ^{235} $ U and$ ^{238} $ U was 10 keV to 20 MeV and 1.5 to 20 MeV, respectively. Note that the neutron count for each channel underwent a change after unfolding. -
The counts from four
$ ^{235} $ U fission cells and four$ ^{238} $ U fission cells are combined to reduce the statistical uncertainty in the counts, after obtaining the unfolded neutron energy spectrum. Combined with Eq. (1), the transmission of the$ ^{\mathrm{nat}} $ Cr sample was obtained. Selecting the neutron total cross-section data of$ ^{\mathrm{nat}} $ Cr from the primary evaluation libraries, the sample thickness equivalent to that used in the experiment was determined. Through calculations, the reference transmission was obtained, and the results were compared, as shown in Fig. 3.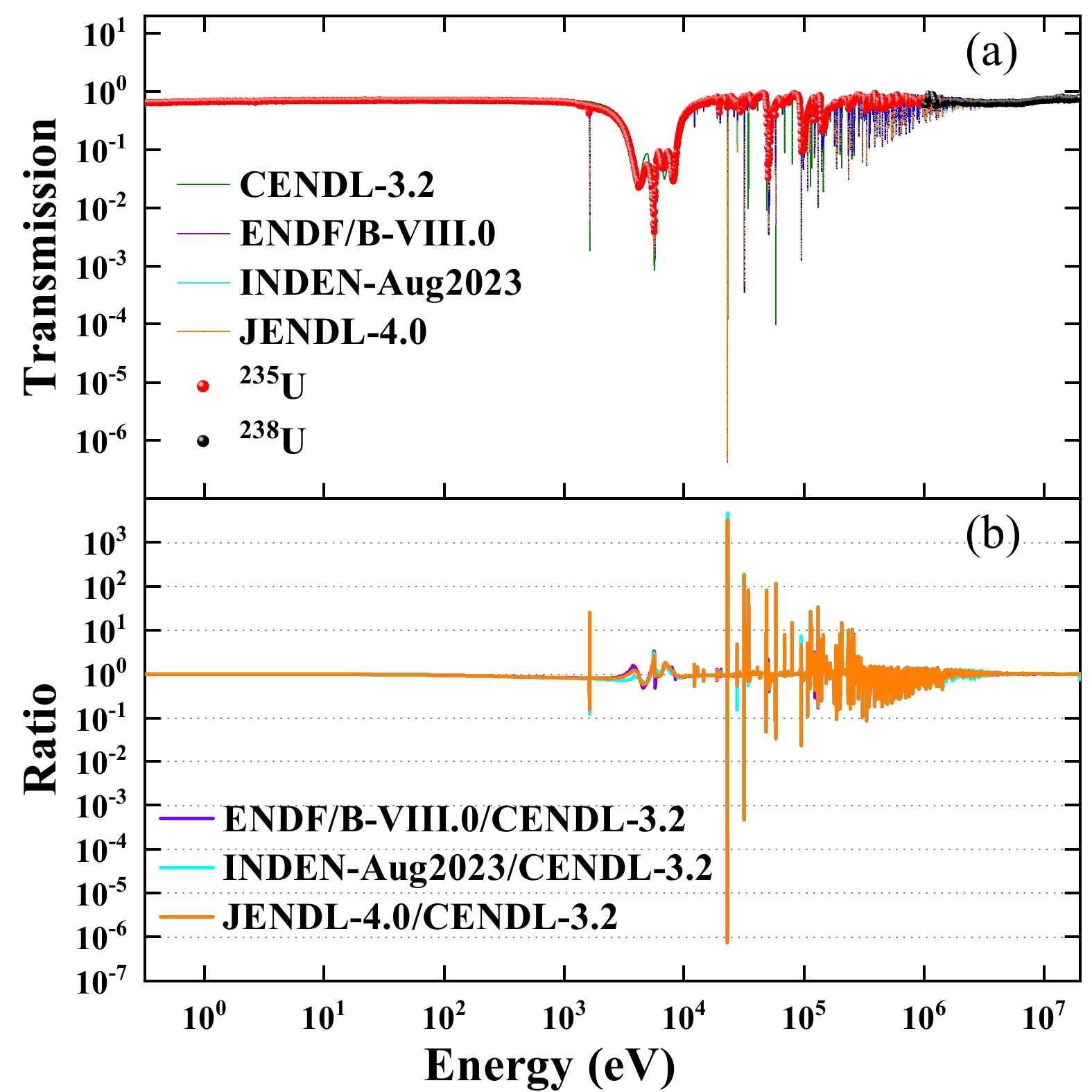
Figure 3. (color online) Neutron transmission of
$ ^{\mathrm{nat}} $ Cr was measured and compared with those in several major nuclear evaluated libraries.As shown in Fig. 3(a), the experimentally measured transmission maintained good agreement with those of several major nuclear evaluated libraries. Figure 3(b) presents the current ratios of various nuclear evaluated databases to CENDL-3.2, revealing significant discrepancies among different nuclear databases, particularly in the high-energy resonance region.
-
The neutron total cross-section is determined by incorporating Eq. (2) after obtaining the transmission. Figure 4 illustrates the comparison between the experimental neutron total cross-section data of
$ ^{\mathrm{nat}} $ Cr obtained in this study and the previously measured data from EXFOR, along with a comparison with those of evaluated libraries (ENDF/B-VIII.0, CENDL-3.2). The measured total cross-sections are generally in good agreement with other existing data and the ENDF/BVIII.0 evaluated data. The data measured by Guber et al. [29] in the energy range of 2 eV to 0.6 MeV generally agree well with the current results. Because the width of proton beam bunches is approximately 30 ns, the extremely narrow resonance peaks observed by Guber et al. were not observed in the current measurement. The data measured by Hibidon et al. [30] generally agree well with the results of this measurement. However, in the energy range of 3 to 9 keV, their measurements were lower than the existing experimental and evaluated data, as shown in Fig. 4(b). Figure 4(f) demonstrates that the data obtained using the$ ^{235} $ U and$ ^{238} $ U fission cells exhibited good consistency, and the results of this study above MeV energy are in good agreement with those measured by Perey et al. and Cierjacks et al. [15, 31].
Figure 4. (color online) Comparison of the neutron total cross-sections of
$ ^{\mathrm{nat}} $ Cr in this study with previous experimental data and evaluated libraries.As indicated by Eq. (2), the uncertainty in the total cross-section primarily arises from the uncertainties in the atomic density of the sample and in the transmission, with the latter being related to the statistical uncertainty in neutron counting. In the process of double-bunch unfolding, uncertainty will also arise. The unfolding code uses an iterative method to calculate the error of each channel, including the error of the fission events as a function of neutron TOF and energy. The uncertainty in the neutron total cross-section can be expressed by Eq. (6).
$ \frac{\Delta \sigma}{\sigma} = \frac{-\sqrt{\left(\frac{\Delta T}{T}\right)^2+(\ln T)^{2}\left[\left(\frac{\Delta d}{d}\right)^{2} + \left(\frac{\Delta n}{n}\right)^{2}\right]+(e_{i})^{2}+(e_{o})^{2}}}{\ln T} $

(6) where
$ e_i $ and$ e_o $ are the uncertainties in unfolding with sample-in and sample-out.Figure 5 shows fluctuations in the uncertainty of the neutron total cross-section measurements of
$ ^{\mathrm{nat}} $ Cr in the energy range of 4 eV to 1.5 keV caused by the material Ta-181 wrapped around the spallation target exhibiting high neutron absorption and resonances of$ ^{235} $ U in this energy range. In the energy range of 0.01 to 1 MeV, significant statistical fluctuations in neutron counts occurred owing to the large neutron resonance cross-section of$ ^{\mathrm{nat}} $ Cr, introducing uncertainty and fluctuations. In the measurement of the neutron total cross-section of$ ^{\mathrm{nat}} $ Cr using$ ^{235} $ U fission cells, approximately 79% of energy points had uncertainties below 5%, 18% had uncertainties between 5 and 10%, and 3% had uncertainties between 10 and 29%. For measurements using$ ^{238} $ U fission cells, approximately 92% of energy points had uncertainties below 5%, 7% had uncertainties between 5 and 10%, and 1% had uncertainties between 10 and 19%.
Figure 5. (color online) Neutron total cross-sections and uncertainties of
$ ^{\mathrm{nat}} $ Cr obtained using$ ^{235} $ U and$ ^{238} $ U cells.When obtaining the fission events as a function of neutron energy, the neutron count corresponding to a particular energy point is the sum of neutron counts within an energy bin range. In regions with significant cross-section variations, this can result in an overestimation of the average neutron count (in areas where the cross-section decreases with energy) or an underestimation (in areas where the cross-section increases with energy). Consequently, this leads to an underestimation or overestimation of the neutron transmission, thus exhibiting a leftward shift in resonance peaks. Fig. 6 depicts a comparison of transmission profiles with different energy bins, illustrating the disparity between employing 100 bins and 600 bins within each order of magnitude.
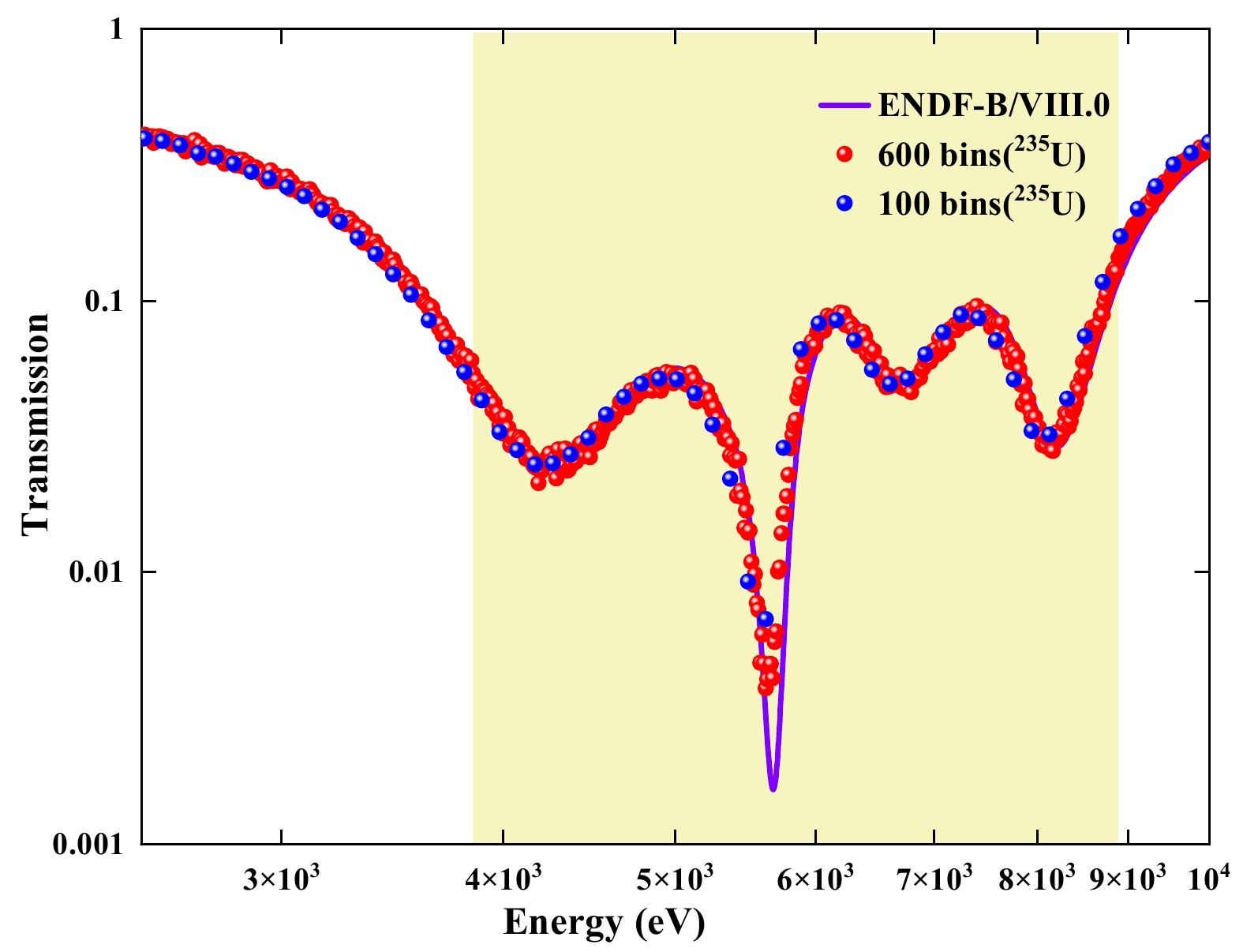
Figure 6. (color online) Comparison of the transmission of
$ ^{\mathrm{nat}} $ Cr using different energy bins.For several transmission valleys caused by resonances within this energy range, a smaller number of bins resulted in a leftward shift, introducing deviations in experimental outcomes. Comparative analysis revealed that within the 0.3 to 20 eV energy range, experimental data with a lower bin count exhibited deviations in all resonance valleys ranging from 0.9 to 2.7%.
Note that when the bin count reached 600, the resonance valleys were no longer shifted. Moreover, excessively large bin values may introduce significant experimental errors, affecting data precision. Considering these factors, this study adopted 100 bins for the energy range below 1.3 keV, where there were no resonance peaks. For the energy range from 1.3 keV to 20 MeV, 600 bins were used to obtain the fission events as a function of neutron energy and proceed with subsequent analyses.
As shown in Fig. 6, after selecting an appropriate bin value of 600, the measured resonance peaks still exhibited slight deviations compared with those of ENDF/B-VIII.0. This is because the energy resolution varies with neutron energy, and the energy resolution function (ERF) affects the broadening and shifting of the resonance peaks in the neutron total cross-section. Resolution broadening in measured data is influenced by (1) finite time intervals required for both the neutron beam and detecting apparatus, including primary beam pulse-burst and time uncertainties in the detector and electronics, and (2) variations in the flight path length of the neutron due to its original position within the neutron-producing target, interaction position with the sample, and detection position. The total resolution broadening is the convolution of these components. The effect of the ERF on the measured data is discussed in more detail in Ref. [32].
-
The neutron total cross-section in the energy range of 1.5 to 20 MeV was theoretically calculated using TALYS-1.96 [33] with default parameters. The calculation of TALYS was not used as a fitting of the measured result, but as a prediction for nuclear reactions and the neutron nuclear cross-section. In this study, all possible exit reaction channels and all associated cross sections of the n+
$ ^{\mathrm{nat}} $ Cr reaction at different neutron energies were considered, and the total cross-section of$ ^{\mathrm{nat}} $ Cr was extracted and analyzed. The results of the theoretically calculated excitation function are also shown in Fig. 7.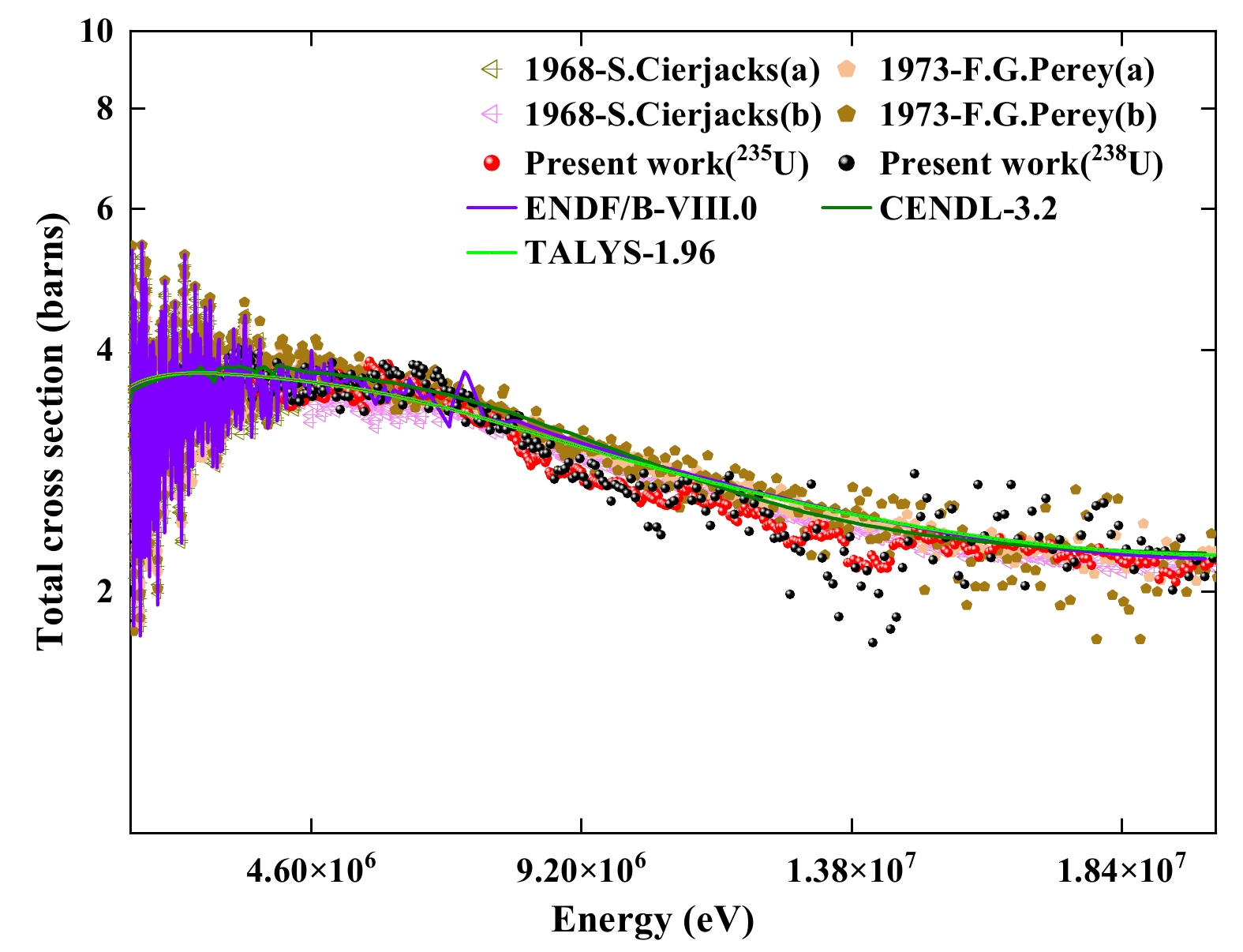
Figure 7. (color online) Measured data are compared with evaluation libraries, theoretical calculation data, and existing experimental data.
The overall trend of the measured data agrees well with both the evaluated databases and the data obtained from the TALYS calculations. Compared with the results measured by Perey et al. and Cierjacks et al., the measured data in this study were slightly lower than those of the evaluated libraries and TALYS calculations. The parameters of relevant nuclear reaction models require further validation using this data.
-
The neutron total cross-sections of
$ ^{\mathrm{nat}} $ Cr in the energy range of 0.3 eV to 20 MeV were measured using the NTOX spectrometer on the Back-n beamline at the CSNS. Offline processing was performed for the acquired full-waveform digital data, including background subtraction, neutron flight time determination, energy calibration, transmission analysis, and neutron total cross-section derivation. The current measurement results are generally in good agreement with existing experimental data and evaluated data in ENDF/B-VIII.0. Therefore, the TALYS-1.96 program was used to calculate the excitation function of the total cross-section of$ ^{\mathrm{nat}} $ Cr in the energy region of 1.5 to 20 MeV. In this study, the neutron total cross-sections of$ ^{\mathrm{nat}} $ Cr was obtained for the first time in one experiment in the energy range of interest for reactor applications. This provides a high-quality data reference and comprehensive uncertainty analysis, facilitating the re-evaluation and improvement of the neutron-induced cross-sections of$ ^{\mathrm{nat}} $ Cr.In the future, a
$ ^{6} $ Li-containing scintillator-based detector will be developed for the application in neutron-induced total cross-section measurements. A fast scintillator-based neutron total cross-section (FAST) spectrometer is under construction, the physical design of which has been completed [34]. The FAST spectrometer has a higher neutron detection efficiency and could provide a reference in the resonance region of$ ^{235} $ U with a lower statistical uncertainty compared with data collected by NTOX. -
The authors would like to thank the operating crew at the CSNS for providing a very stable neutron beam for measurements.
New measurement of the neutron-induced total cross-sections of natCr in a wide energy range on the Back-n at CSNS
- Received Date: 2024-04-19
- Available Online: 2024-10-15
Abstract: The neutron total cross-section of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: