-
The emergence of regular collective motions in complex many-body systems has become one of the most fascinating and fruitful subjects in quantum physics. In nuclear physics, the collective rotational modes associated with quadrupole deformations of nuclei can be well illustrated within a Bohr-Mottelson picture of the dynamics using geometric language [1], which can be extended to include the axially-deformed rotor, triaxially-deformed rotor, γ-unstable rotor, and spherical vibrator modes. These collective modes have been demonstrated equivalently well within the interacting boson model (IBM) using group or algebraic language [2], including U(5) (spherical vibrator),
$S U$ (3) (axially-deformed rotor), and O(6) (γ-unstable rotor). From an experimental perspective, these collective modes can be readily recognized by inspecting the spectroscopy and electromagnetic transition observables related to yrast states. The most common quantities are the energy ratio$ R_{4/2}= E(4_1^+)/E(2_1^+) $ and$ B(E2) $ ratio$ B_{4/2}= B(E2;4_1^+\rightarrow 2_1^+)/ B(E2;2_1^+\rightarrow0_1^+) $ [3]. These are characterized by$ R_{4/2}\approx $ 2.0 and$ B_{4/2}\approx2.0 $ for U(5),$ R_{4/2}\approx3.3 $ and$ B_{4/2}\approx 1.4$ for$S U$ (3), and$ R_{4/2}\approx2.5 $ and$ B_{4/2}\approx1.4 $ for O(6). Although the different collective modes cannot be easily distinguished using B(E2) ratios, they all show a common feature of$ B_{4/2}>1.0 $ , together with$ R_{4/2}\geq2.0 $ . For a long time, this has been considered as a robust rule for nuclear collective modes, as it is consistent with various theoretical calculations and the large amount of experimental data on collective nuclei [1].The global development of large-scale radioactive beam facilities, including the HIAF in China, FAIR in Europe, FRIB in USA, and RIBF in Japan, have made it possible to explore exotic nuclei with extreme ratios of proton and neutron numbers, which can exhibit dynamic shell structures very different from traditionally known ones, as well as new kinds of collective motions (e.g., see Refs. [4, 5] and references therein). In particular, an anomalous collective motion characterized by
$ R_{4/2}\geq2.0 $ and$ B_{4/2}<1.0 $ was observed recently in some neutron deficient nuclei [5−9] near$ N_{n}=90 $ and the proton dripline. Such an unusual feature can neither be understood from the familiar conventional collective modes nor be reproduced by large-scale shell models or beyond mean-field approaches, presenting a great challenge for nuclear theory [6]. In addition, a similar phenomenon was observed to occur in odd-mass nuclei [9], where the situation becomes more complicated due to the mixing between collective and single-particle degrees of freedom [10], as indicated by different microscopic approaches, such as those based on nuclear energy density functionals [11−14]. To date, most existing research on$ B(E2) $ anomalies have focused on experimental aspects [5−9, 15−18] and even-even nuclei. It is still unclear whether the odd-even and even-even systems associated with the anomalous$ E2 $ structures can be dynamically correlated with each other. Therefore, theoretical investigations of$ B(E2) $ anomalies are urgently needed to elucidate the possible mechanism behind this phenomenon.In this study, an algebraic scheme including three-body boson interactions is proposed within the IBM framework to study the influence of triaxial modes on
$ B(E2) $ transitions. We show that the proposed model can offer a unified description of the$ B(E2) $ anomalous structures of the Os nuclei with both even and odd mass numbers. -
Hamiltonian and physical operators in the IBM [2] are constructed from two kinds of boson operators: the s boson with
$ J^\pi=0^+ $ and the d boson with$ J^\pi=2^+ $ . Among them, the angular momentum and quadrupole operators are defined by$ \begin{array}{*{20}{l}} &&\hat{L}_u=\sqrt{10}(d^\dagger\times\tilde{d})_u^{(1)}\, , \end{array} $

(1) $ \begin{array}{*{20}{l}} &&\hat{Q}_u^\chi=(d^\dagger\times\tilde{s}+s^\dagger\times\tilde{d})_u^{(2)}+\chi(d^\dagger\times\tilde{d})_u^{(2)}\, \end{array} $

(2) with the parameter
$ \chi\in [0,-{\sqrt{7}}/{2} ] $ . One can prove that these operators will generate the$S U$ (3) algebra when$ \chi=- {\sqrt{7}}/{2} $ and become a part of the O(6) algebra when$ \chi=0 $ . Another operator frequently employed in the IBM is the d boson number operator:$ \hat{n}_{d}=\sum\limits_md_m^\dagger d_m\, , $

(3) which is simultaneously the 1st-order Casimir operator of the U(5) algebra [2] and to some extent reflects the influence of the pairing interaction between valence nucleons [19]. It is shown below that the widely discussed consistent-Q Hamiltonian [20] in the IBM is simply constructed by the operators defined above.
-
A big advantage of the IBM is that the finite-N effect in a nucleus has been reasonably taken into account by having the total boson number N equal to the number of valence nucleon pairs. An early study [21] of the rotor modes in the IBM even showed that the
$ B(E2;L\rightarrow L-2) $ values for yrast states may decrease as a function of L in a finite triaxial system, which provides a theoretical clue towards producing a depressed$ B(E2) $ cascade structure with$ B_{4/2}<1.0 $ . It was recently justified [22] that the$S U$ (3) IBM realization of a triaxial rotor [21, 23−25] can indeed yield the$ B(E2) $ anomaly features with$ B_{4/2}\ll1.0 $ , as observed in some neutron-deficient nuclei. Another recent work [26] based on the IBM framework showed that a combination of the 2nd- and 3rd-order$S U$ (3) Casimir operators [27], which will allow a region of triaxiality after adding the U(5) term [28], may generate a similar$ E2 $ anomalous structure. These studies suggest the necessity of introducing triaxial modes to generate such anomalous$ E2 $ -related behavior. Nevertheless, these schemes were only applied to describe the even-mass systems, while their descriptions of the$ B(E2) $ anomaly phenomenon greatly rely on the languages of the$S U$ (3) irreducible representations [24, 25, 29]. In this study, we propose a different way to generate triaxial modes in the IBM, and the resulting model is shown to be able to yield the required$ E2 $ anomalous features in both even- and odd-mass nuclei.It has been long known [30] that the cubic interaction term
$ (d^\dagger\times d^\dagger\times d^\dagger)^{(3)}\cdot(\tilde{d}\times\tilde{d}\times\tilde{d})^{(3)} $ in the IBM can induce triaxial deformation in its classical potential function. Specifically, a stable triaxial minimum can be induced at the mean-field level by adding this term to the O(6) limit of the IBM [31, 32]. The resulting dynamical influences have been applied to improve the traditional IBM descriptions of Xe, Ba, Os, and Er isotopes [31−35]. In particular, it has been shown [36] that the strength parameters for similar cubic terms in the proton-neutron IBM could even be microscopically determined from the potential energy surfaces obtained from the nuclear energy density functionals, by which the theoretical descriptions of the γ bands in heavy nuclei can be clearly improved without any need for phenomenological adjustments. Another important cubic interaction term is$ (\hat{L}\times\hat{Q}^\chi\times\hat{L})^{(0)} $ , which has been widely addressed in previous IBM descriptions of rotational dynamics [21, 23, 37−39]. Although this term itself cannot induce a stable triaxial deformation [22, 37, 38], it may mix states with the same spin in neighboring rotational bands. For instance, the degeneracy in the first β and γ bands in an axially-deformed system described by the two-body$S U$ (3) interactions will be removed by adding this term [37]. Thus, it is anticipated that this cubic term can similarly contribute to band mixing in a triaxial system [39].Based on the above considerations, the model Hamiltonian is designed as follows:
$ \begin{aligned}[b] \hat{H}_\mathrm{B}=\;&\epsilon\hat{n}_d+ \frac{\kappa}{N}\Bigg[\hat{Q}^\chi\cdot \hat{Q}^\chi+a\frac{(d^\dagger\times d^\dagger\times d^\dagger)^{(3)}\cdot(\tilde{d}\times\tilde{d}\times\tilde{d})^{(3)}}{N}\\ &+b\frac{(\hat{L}\times\hat{Q}^\chi\times\hat{L})^{(0)}}{N}+c\hat{L}^2\Bigg]\, , \end{aligned} $

(4) where
$ \epsilon,\; \kappa,\; a,\; b $ , and c are real parameters, and N represents the total boson number. To solve this Hamiltonian, the eigenstates can be expanded in terms of the${U(6)}\supset S U(3) \supset S O(3) \supset S O(2)$ basis vectors as$ |\alpha LM_L\rangle=\sum\limits_{(\lambda,\mu)\tilde{\chi}}C_{(\lambda,\mu)\tilde{\chi}}^{\alpha,L}|N(\lambda,\mu)\tilde{\chi}LM_L\rangle\, , $

(5) where α generally denotes the other quantum numbers, in addition to angular momentum.
$ C_{(\lambda,\mu)\tilde{\chi}}^{\alpha,L} $ are the expansion coefficients, with$ (\lambda,\mu) $ labeling the$S U$ (3) irreducible representations and$ \tilde{\chi} $ denoting the multiplicity in the reduction${S U(3)}\downarrow {S O(3)}$ . Clearly, by taking$ a=b= c= 0 $ , the Hamiltonian (4) will be exactly reduced to the well known consistent-Q Hamiltonian [20],$ \hat{H}_\mathrm{CQ}=\epsilon\hat{n}_d+ \frac{\kappa}{N}\hat{Q}^\chi\cdot \hat{Q}^\chi\, , $

(6) which has often been employed to describe the dynamical evolution between the different symmetry limits of the IBM. Specifically,
$ \hat{H}_\mathrm{CQ} $ describes the U(5) limit when$ \varepsilon>0 $ and$ \kappa=0 $ ; the O(6) limit when$ \varepsilon=0 $ ,$ \kappa<0 $ , and$ \chi=0 $ ; and the$S U$ (3) limit when$ \varepsilon=0 $ ,$ \kappa<0 $ , and$ \chi=-\sqrt{7}/{2} $ . These three limits in turn correspond to three typical collective modes, as mentioned above. However, an IBM Hamiltonian up to two-body terms, such as$ \hat{H}_{\mathrm{CQ}} $ , cannot yield a stable triaxial deformation and the associated modes linked to the triaxial rotor [40], which has been extensively employed to elucidate nuclear excitation correlated with triaxiality in both even [41] and odd nuclei [42−44]. The Hamiltonian given in (4), which can be considered as an extension of the consistent-Q formula in (6), overcomes this limitation and can therefore be applied to demonstrate all typical quadrupole modes, including triaxial rotor. To justify this at the mean-field level, an analysis of the classical potentials is presented below.The classic limit of an IBM Hamiltonian can be determined based on the coherent state defined by [2]
$ |\beta, \gamma, N\rangle=G[s^\dagger + \beta \mathrm{cos} \gamma\; d_0^\dagger\ + \frac{1}{\sqrt{2}} \beta \mathrm{sin} \gamma (d_2^\dagger + d_{ - 2}^\dagger)]^N |0\rangle\, $

(7) with
$ G=1/\sqrt{N!(1+\beta^2)^N} $ . The classical potential function corresponding to$ \hat{H}_\mathrm{B} $ is then derived as$ \begin{aligned}[b] V(\beta,\gamma)_\mathrm{B}=\;&\frac{1}{N}\langle\beta, \gamma, N|\hat{H}_\mathrm{B}|\beta, \gamma,N\rangle|_{N\rightarrow \infty}\\ =\;&\epsilon\frac{\beta^2}{1+\beta^2}+\kappa\frac{4\beta^2-4\sqrt{\dfrac{2}{7}}\chi\beta^3\mathrm{cos}(3\gamma)+\dfrac{2}{7}\chi^2\beta^4}{(1+\beta^2)^2}\\ &+\kappa a\frac{\beta^6[\mathrm{cos}^2(3\gamma)-1]}{7(1+\beta^2)^3}\, , \end{aligned} $

(8) using which the ground-state energy per boson is determined by minimizing the potential with respect to β and γ. Note that the last two terms in (4) involving the angular momentum operator
$ \hat{L} $ are proven to contribute nothing to the large-N (classical) limit. As expressed in Eq. (8), the potential function exhibits a dependence on$ \mathrm{cos}^2(3\gamma) $ in its third term, which implies that triaxial deformation will be allowed by the present Hamiltonian [30]. By contrast, the potential function corresponding to the consistent-Q Hamiltonian only encompasses the first two terms of (8). For better visualization, the potential surfaces generated from (8) for different cases are presented in Fig. 1. It is shown that the U(5) potential reaches its minimum at$ \beta_\mathrm{e}=0 $ , signifying a spherical shape; the$S U$ (3) one reaches its minimum at$ \gamma_\mathrm{e}=0^\circ $ , corresponding to prolate deformation; and the O(6) potential manifests a γ-unstable picture with its minimum being independent of γ. These potentials are actually those derived from the consistent-Q Hamiltonian without considering three-body terms. The most noteworthy case is the one denoted by O(6)$ _{\mathrm{Tri}.} $ , as shown in Fig. 1(D). The results indicate that a stable triaxial deformation can be developed at the mean-field level after adding the six-d term to the O(6) limit, which agrees well with the previous analysis presented in [32]. This suggests that collective modes for various quadrupole deformations can be equally addressed using the model Hamiltonian (4).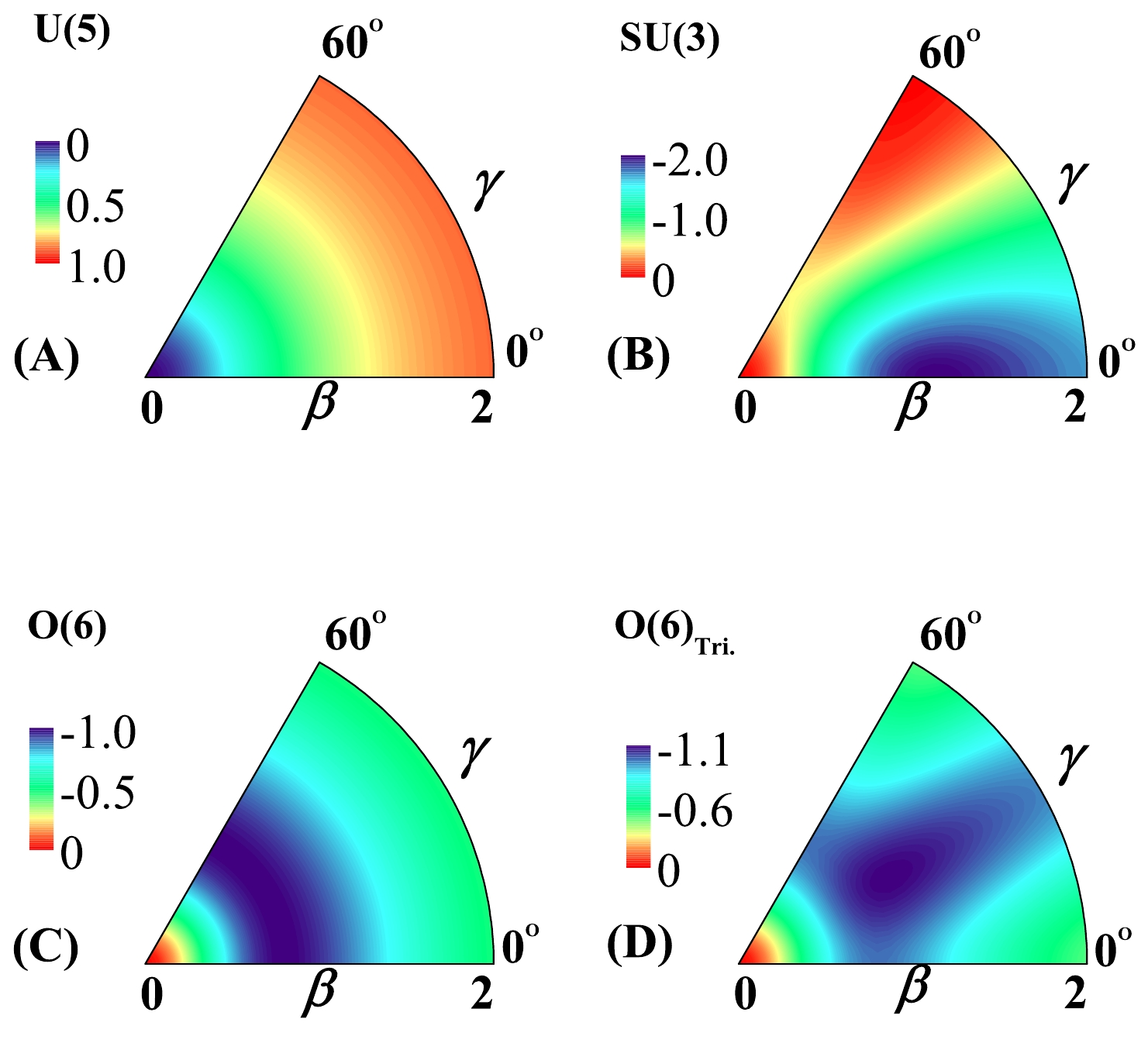
Figure 1. (color online) Potential surfaces extracted from Eq. (8) with nonzero parameters adopted as
$ \varepsilon=1.0 $ for U(5);$ \kappa=-1.0 $ and$\chi=- {\sqrt{7}}/{2}$ for$S U$ (3);$ \kappa=-1.0 $ and$ \chi=0 $ for O(6); and$ \kappa=-1.0 $ ,$ \chi=0 $ , and$ a=-5.5 $ for O(6)$ _{\mathrm{Tri}} $ .To determine whether a depressed
$ E2 $ structure can be produced in the present scheme, the ratios$ R_{4/2} $ and$ B_{4/2} $ solved from$ \hat{H}_\mathrm{B} $ for different transitional regions are examined. For convenience, the strength parameters in (4) have been rewritten as$ \epsilon=(1-\eta) $ and$ \kappa=-{\eta}/{4} $ , using which the U(5)-O(6) transition is characterized by$ \eta\in[0, 1] $ and$ \chi=0 $ ; the U(5)-$S U$ (3) transition by$ \eta\in[0, 1] $ and$ \chi=-\sqrt{7}/2 $ ; and the$S U$ (3)-O(6) transition by$ \chi\in[-\sqrt{7}/2,0] $ and$ \eta=1 $ . Furthermore, two sets of dimensionless parameters,$ (a,b,c)=(-5.5,2.0,-0.5) $ and$ (a,b,c)=(0,0,0) $ , are considered for numerical investigation; the former ensures that$ \hat{H}_\mathrm{B} $ at the O(6) point ($ \eta=1 $ and$ \chi=0 $ ) generates a stable triaxial deformation, as depicted in Fig. 1(D), while the latter may yield results consistent with the consistent-Q Hamiltonian, leading to a γ-unstable picture in the O(6) limit, as shown in Fig. 1(C).Throughout this paper, the
$ E2 $ transitional operator is simply adopted as$ \begin{array}{*{20}{l}} \hat{T}^{E2}=e\hat{Q}^\chi\, \end{array} $

(9) where e denotes the effective charge, and χ takes the same value as in the Hamiltonian. Then, the reduced
$ B(E2) $ transitional probability can be evaluated via$ B(E2;L_i\rightarrow L_f)=\frac{|\langle \alpha_fL_f\parallel\hat{T}^{E2}\parallel \alpha_iL_i\rangle|^2}{2L_i+1}\, . $

(10) With the reset parameters, the results for
$ R_{4/2} $ and$ B_{4/2} $ solved from$ \hat{H}_\mathrm{B} $ are shown in Fig. 2 to present a comparison across different transitional situations. As shown in Fig. 2, the evolution of$ R_{4/2} $ values for$ H_\mathrm{B} $ closely resembles that for$ H_\mathrm{CQ} $ in each transitional region. Notably, the ratio values in all cases are maintained within$ 2.0\leq R_{4/2}\leq3.33 $ , as expected for a collective mode. Regarding the$ B_{4/2} $ ratio, the results indicate a significant difference between the present model and consistent-Q Hamiltonian, particularly for the$S U$ (3)-O(6) transitional case, as depicted in Fig. 2(f). It is shown that the ratio in the present model (denoted by$ H_\mathrm{B} $ ) may decrease to very low values with$ B_{4/2}<1.0 $ over a wide range of χ, contrasting with the nearly constant evolution with$ B_{4/2}\sim1.4 $ (denoted by$ H_\mathrm{CQ} $ ) produced by the consistent-Q Hamiltonian. This striking feature suggests that an anomalous$ E2 $ structure is more readily produced in the current model that involves various collective modes, including the triaxial rotor. In fact, it can be observed from Fig. 2(e) that the$ B_{4/2} $ value in the present model at the O(6) point, which may give rise to the O(6)$ _{\mathrm{Tri}} $ potential shown in Fig. 1(D), is already much smaller than that obtained from the traditional O(6) mode described by$ \hat{H}_\mathrm{CQ} $ . Further numerical calculations indicate that the potentials corresponding to the cases with$ B_{4/2}\ll1.0 $ around$ \chi\sim-0.3 $ may still preserve their minima with$ 60^\circ>\gamma_\mathrm{e}>0^\circ $ , as shown in Fig. 2 (f). The above results demonstrate that a certain triaxial component is indeed essential for producing$ B(E2) $ anomalies in theory [22].
Figure 2. (color online) Upper:
$R_{4/2}$ values solved from the model Hamiltonian (4) in the U(5)-$ $ $S U$ (3), U(5)-O(6), and$S U$ (3)-O(6) transitional regions, where$H_\mathrm{B}$ and$H_{\mathrm{CQ}}$ denote the results obtained for$(a,b,c)=(-5.5,2.0,-0.5)$ and$(a,b,c)=(0,0,0)$ , respectively (see text for the other parameters). Lower: same as in the upper row but for the ratio$B_{4/2}$ . The thick (blue) line in panel (f) represents$B_{4/2}=1.0$ . The total boson number in the calculations is set to$N=8$ . -
To elucidate the
$ E2 $ -related behaviors in odd-mass systems, the algebraic scheme proposed above must be extended from the IBM to the interacting boson-fermion model (IBFM) [45]. A Hamiltonian in the IBFM can generally be expressed as$ \begin{array}{*{20}{l}} \hat{H}=\hat{H}_\mathrm{B}+\hat{H}_\mathrm{F}+\hat{V}_{\mathrm{BF}}\, , \end{array} $

(11) where
$ \hat{H}_{\mathrm{B}} $ is the IBM Hamiltonian describing the boson core,$ \hat{H}_{\mathrm{F}} $ denotes the fermion Hamiltonian describing the unpaired fermions, and$ \hat{V}_{\mathrm{BF}} $ denotes the boson-fermion interaction [46−49]. Owing to the dynamical correlation between neighboring even-even and odd-even systems, the IBM Hamiltonian$ \hat{H}_\mathrm{B} $ takes the same form as defined in (4). For low-energy excitation, often only one unpaired fermion is considered. The fermion Hamiltonian for a single particle is then written as$ \hat{H}_{\mathrm{F}}=\sum\limits_{jm}\varepsilon_j\; a_{jm}^\dagger a_{jm} $ , where$ a_{jm}^\dagger\; (a_{jm}) $ is the creation (annihilation) operator for an odd particle, and$ \varepsilon_j $ denotes single-particle energies. It is further assumed that the unpaired fermion is confined to move within a specific single-j orbit, consistent with our study cases. This implies that the single Hamiltonian$ \hat{H}_{\mathrm{F}} $ in this scenario may contribute merely a constant and thus be set to zero for convenience. Regarding the boson-fermion interactions, we consider only the most important quadrupole-quadrupole term [47], which is defined as [45]$ \begin{array}{*{20}{l}} \hat{V}_{\mathrm{BF}}=\Gamma\hat{Q}^\chi\cdot\hat{q}_j\, \end{array} $

(12) with the quadrupole operators
$ \hat{Q}^\chi $ given by (2) and$ \hat{q}_j=(a_j^\dagger\times\tilde{a}_j)^{(2)} $ . Another interaction term called exchange interaction, which takes into account the fact that the bosons are fermion pairs [45], is often adopted for a detailed reproduction of low-energy structures of odd-mass nuclei [14], especially the ordering of different rotational bands [45]. Because only yrast bands are involved in the present analysis of the odd-A systems due to limited data availability, we omit this term in the following discussions for simplicity, as done in [47] . Clearly, in addition to being influenced by the boson-fermion interaction, the low-lying properties of an odd-even system in the present scheme are somewhat determined by its core dynamics. In other words, if the$ B(E2) $ anomaly phenomenon appears in an even-even system, it is highly possible to observe a similar phenomenon in its neighboring odd-even partner. This point can be partially understood from the matrix elements of the quadrupole operator in the weak-coupling limit of the model, which may exactly occur for$ \Gamma=0 $ .The
$ B(E2) $ anomaly in odd-even and even-even systems can be characterized by$ B_{4/2}=B(E2;j+4\rightarrow j+2)/ B(E2;j+2\rightarrow j)<1.0 $ , where j represents the single-particle spin in the former and is set to zero in the latter. In the weak-coupling limit, the eigenvector of the odd-even system can be expressed as$|\alpha JM_J\rangle=\sum\limits_{M_L,m_j}\langle L M_L j m_j|J M_J\rangle|\alpha L M_L\rangle|jm_j\rangle\, , $

(13) where
$ |\alpha LM_L\rangle $ and$ |jm_j\rangle=a_{jm_j}^\dagger|0\rangle $ denote the eigenvectors for the even-even core and single particle, respectively. For simplicity, we apply the$ E2 $ operator defined in (9) to calculate the$ B(E2) $ transitions for odd-mass systems as well. By employing the Wigner-Eckart theorem, one can further demonstrate that the reduced matrix element of the quadrupole operator between the vectors defined in (13) satisfies$ \frac{\langle\alpha J-2\| \hat{Q}^\chi\|\alpha J\rangle}{\langle\alpha L-2\| \hat{Q}^\chi\|\alpha L\rangle}=\sqrt{\frac{2J+1}{2L+1}}\, . $

(14) This means that the reduced
$ B(E2) $ transitional probabilities in an odd-even system, which can be evaluated via$ B(E2;J_i\rightarrow J_f)=\frac{|\langle \alpha_fJ_f\parallel\hat{T}^{E2}\parallel \alpha_iJ_i\rangle|^2}{2J_i+1}\, , $

(15) will be entirely dictated by its even-even core, yielding the same
$ B_{4/2} $ values. Although this ideal situation is not expected to truly occur in a realistic nuclear system, the derived result inspires us to "see" the B(E2) anomaly in neighboring odd- and even-mass systems in a unified manner. In more general cases with$ \Gamma\neq0 $ , the model solutions cannot be written as in Eq. (13) but can instead be solved by diagonalizing the IBFM Hamiltonian under the weak-coupling basis:$ |N(\lambda,\mu)\tilde{\chi}(Lj) JM_J\rangle\equiv\sum\limits_{M_Lm_j}\langle L M_L j m_j|J M_J\rangle|N(\lambda,\mu)\tilde{\chi}LM_L\rangle|jm_j\rangle\, , $

(16) where
$ |N(\lambda,\mu)\tilde{\chi}LM_L\rangle $ denotes the$S U$ (3) basis vectors, which are the same as those defined in (5). -
Experimentally, neutron-deficient Os isotopes provide a laboratory for investigating
$ B(E2) $ anomalies. Specifically, unusually low values of$B_{4/2}= B(E2;4_1^+\rightarrow2_1^+)/ B(E2; 2_1^+ \rightarrow 0_1^+)$ have been observed in$ ^{168,170} $ Os by measuring the lifetime of the low-lying excited states [6, 8], thereby providing two compelling examples of the$ B(E2) $ anomaly with$ B_{4/2}<1.0 $ . Similarly, a rather small value of$ B(E2;21/2^+\rightarrow17/2^+)/ B(E2;17/2^+\rightarrow13/2^+) $ was found to manifest in$ ^{169} $ Os for the band built on$ \nu i_{\; 13/2} $ [9], indicating that the$ B(E2) $ anomaly can also occur in odd-mass systems. Additionally, the same$ B(E2) $ ratio is shown to be enhanced significantly in the neighbouring odd-even nucleus,$ ^{171} $ Os [9], although its value still holds for$ B_{4/2}\leq1.0 $ within error bars. To test the present algebraic scheme in explaining these exotic$ E2 $ structures, we first apply the boson Hamiltonian (4) to describe$ ^{168,170} $ Os and then employ its IBFM extension defined in (11) to describe$ ^{169,171} $ Os. -
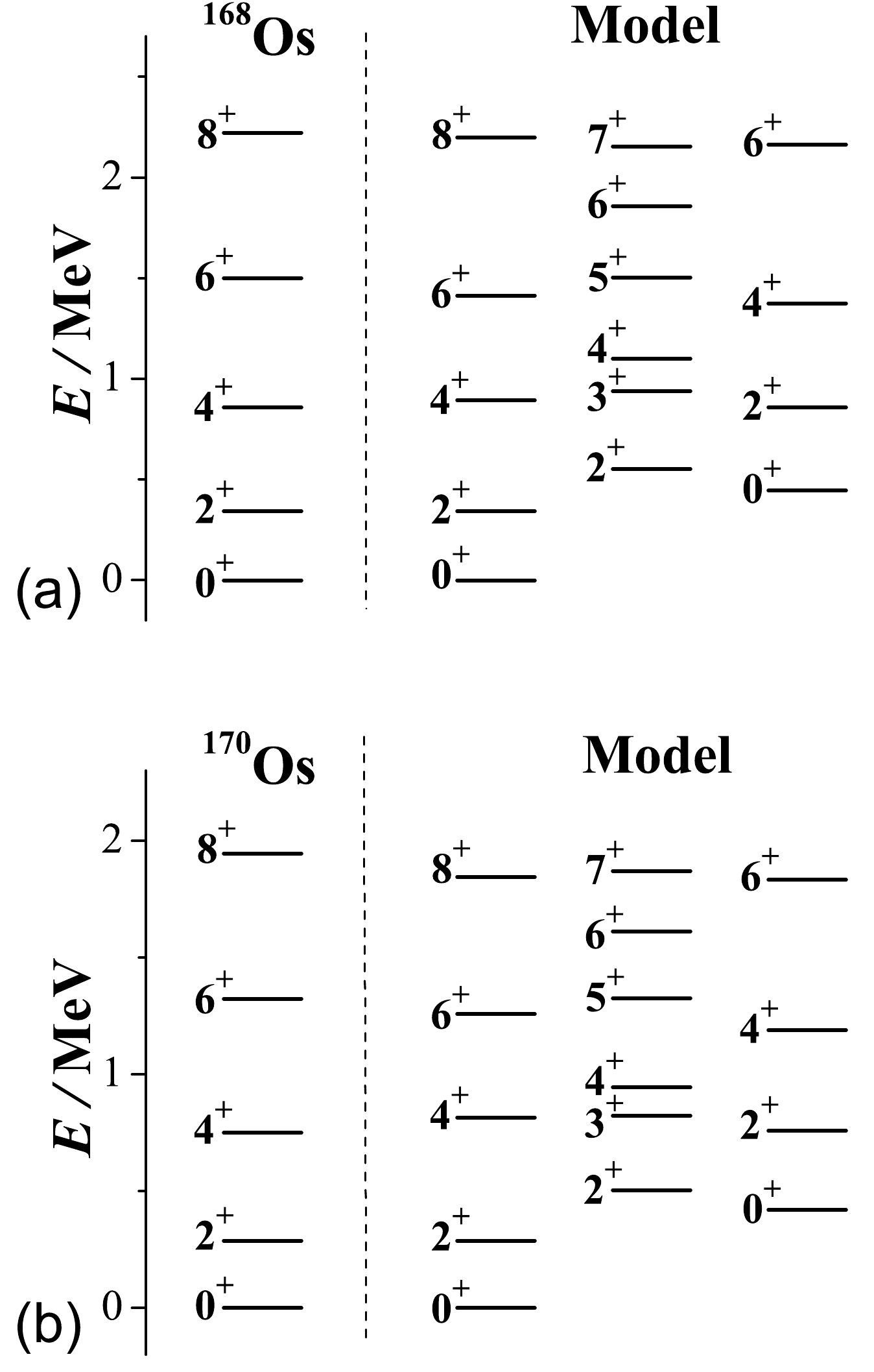
As discussed above, the extended CQ Hamiltonian (4) can generate collective structures with
$ B_{4/2}<1.0 $ by introducing two triaxiality-related cubic interactions. The neutron-deficient$ ^{168,170} $ Os nuclei are expected to be more or less triaxially deformed according to the analysis in [8, 50]. Therefore, it is reasonable to apply the present model to describe the low-lying properties of these two nuclei. Due to limited data availability, only those for the yrast states in$ ^{168,170} $ Os are provided to compare with theoretical calculations. In this context, the model parameters for$ ^{168} $ Os($ ^{170} $ Os) are chosen as$ \varepsilon=0.276(0.250) $ MeV and$ \kappa=-0.12(-0.115) $ MeV while fixing the dimensionless parameters as$ a=-3.2,\; b=7.84,\; c=-1.1 $ , and$ \chi=-0.98 $ . As shown in Fig. 2, the low-lying yrast levels in both Os nuclei can be well reproduced by the model calculations, which predict the low-energy β and γ bands, indicating triaxially. More importantly, one can see from Table 1 that the significantly suppressed$ B_{4/2} $ ratio in$ ^{168,170} $ Os is reasonably described by the theoretical results, which further implies that the anomalous$ E2 $ behavior associated with$ B(E2;L_1^+\rightarrow (L-2)_1^+)/ B(E2;2_1^+\rightarrow0_1^+)<1.0 $ may persist even for yrast states with$ L>4 $ . These predictions actually suggest a robust test of the present model calculations in future experiments for low-lying non-yrast states, as producing$ B_{4/2}<1.0 $ in theory will impose stringent constraints on the model parameters, as indicated in Fig. 2(f). In addition, the results presented in Table 1 confirm that traditional collective modes such as U(5),$S U$ (3), and O(6), even when taking into account the finite-N effects, cannot account for the$ B(E2) $ anomaly phenomenon. It should be noted that the present results obtained from fitting the low-lying properties of$ ^{168,170} $ Os are qualitatively similar to those given in [22] and [26], where two different Hamiltonians were employed in the IBM. A commonality beetween these models is that they all may contain triaxial rotor modes and incorporate triaxial deformations under the given parameters due to the introduction of the high-order terms. The difference is that a clear triaxial picture can be achieved in a very simple way in the current approach in contrast to the previous schemes, where the high-order$S U$ (3) Casimir operators are specifically required in their Hamiltonian constructions. Therefore, the present analysis evidently reveals the connection between the$ B(E2) $ anomaly features and possible triaxiality in neutron-deficient nuclei.$ L_i^\pi\rightarrow L_f^\pi $ 

$ ^{168} $ Os

Model $ ^{170} $ Os

Model U(5) $S U$ (3)

O(6) $ 2_1^+\rightarrow0_1^+ $ 

100 100 100 100 100 100 100 $ 4_1^+\rightarrow2_1^+ $ 

34(18) 40 38(11) 50 178 139 137 $ 6_1^+\rightarrow4_1^+ $ 

− 32 − 28 233 146 150 $ 8_1^+\rightarrow6_1^+ $ 

− 23 − 22 267 141 149 $ 2_2^+\rightarrow2_1^+ $ 

− 79 − 49 178 0.0 137 $ 0_2^+\rightarrow2_1^+ $ 

− 10 − 9 178 0.0 0.0 Table 1. Calculated
$ B(E2) $ results for$ ^{168} $ Os [6] and$ ^{170} $ Os [8], normalized to$ B(E2;2_1^+\rightarrow0_1^+)=100 $ , are presented to compare with the available data. Here, "-" indicates unknown experimental data. In addition, the results for the three symmetry limits derived from$ \hat{H}_{\mathrm{CQ}} $ with$ N=9 $ are included for comparative analysis. -
To further analyze the adjacent odd-A systems, we apply the model to calculate the yrast levels and associated
$ E2 $ transitions in$ ^{169,171} $ Os for the band built on the single-j orbit$ \nu{i_{13/2}} $ , as only data relevant to yrast states are currently available [9]. To assess the impact of the single particle on the suppressed$ B(E2) $ structures, we first examine how the$ R_{4/2} $ and$ B_{4/2} $ ratios evolve with respect to the boson-fermion interaction strength. In the present case, the two ratios are defined as$ R_{4/2}=E(21/2^+)/ E(17/2^+) $ and$ B_{4/2}=B(E2;21/2^+\rightarrow17/2^+)/ B(E2;17/2^+\rightarrow 13/2^+) $ due to the given single-particle spin$ j=13/2 $ . As shown in Fig. 3, the$ R_{4/2} $ values may decrease monotonically as a function of$ \Gamma/\epsilon $ , while the$ B_{4/2} $ values exhibit a non-monotonic evolution approximately symmetric around$ \Gamma/\epsilon=0 $ . Furthermore, the results indicate that slightly reducing$ \kappa/\epsilon $ has a minor effect on the values of$ R_{4/2} $ but leads to a noticeable increase in values of$ B_{4/2} $ .For a clearer illustration of the evolution of the
$ E2 $ anomalous structures, the experimental values of$ R_{4/2} $ and$ B_{4/2} $ are shown in Fig. 4 and compared with the theoretical calculations for$ ^{168-171} $ Os. Two calculations are presented. In the first group of calculations for$ ^{169,171} $ Os, all the model parameters involved in the core Hamiltonian$ \hat{H}_\mathrm{B} $ remain consistent with those for the adjacent even-even nuclei ($ ^{168,170} $ Os), except for a slight adjustment to$ \kappa=-0.1 $ MeV for both nuclei. For the boson-fermion interaction$ \hat{V}_{\mathrm{BF}} $ , the strength parameter is adopted as$ \Gamma=-0.02 $ MeV for$ ^{169} $ Os and$ \Gamma=-0.01 $ MeV for$ ^{171} $ Os, corresponding to$ \Gamma/\epsilon=-0.07 $ and$ \Gamma/\epsilon=-0.04 $ , respectively. As illustrated in Table 2, the yrast levels and depressed$ B_{4/2} $ in experiments can be generally well described by the calculated results, especially for$ ^{169} $ Os. This means that the correlation between the neighbouring odd- and even-mass Os nuclei associated with$ B(E2) $ anomalies is reasonably reflected by the model calculations. In addition, it is noteworthy that the$ B(E2) $ ratios for the yrast states in$ ^{171} $ Os [9] may approach unity, in contrast to the much depressed$ B_{4/2} $ value in$ ^{170} $ Os, as listed in Table 1. This dramatic change is not well reproduced theoretically if the model parameters are solely determined from the even-even core. Therefore, we readjust the model parameters by setting$ \kappa=-0.115 $ (in MeV),$ b=4.7 $ , and$ \chi=-0.5 $ to better fit the data for$ ^{171} $ Os. The calculated results denoted by the superscript "a" given in Table 2 now align more closely with the available data, particularly for the much enhanced$ B(E2) $ transitions.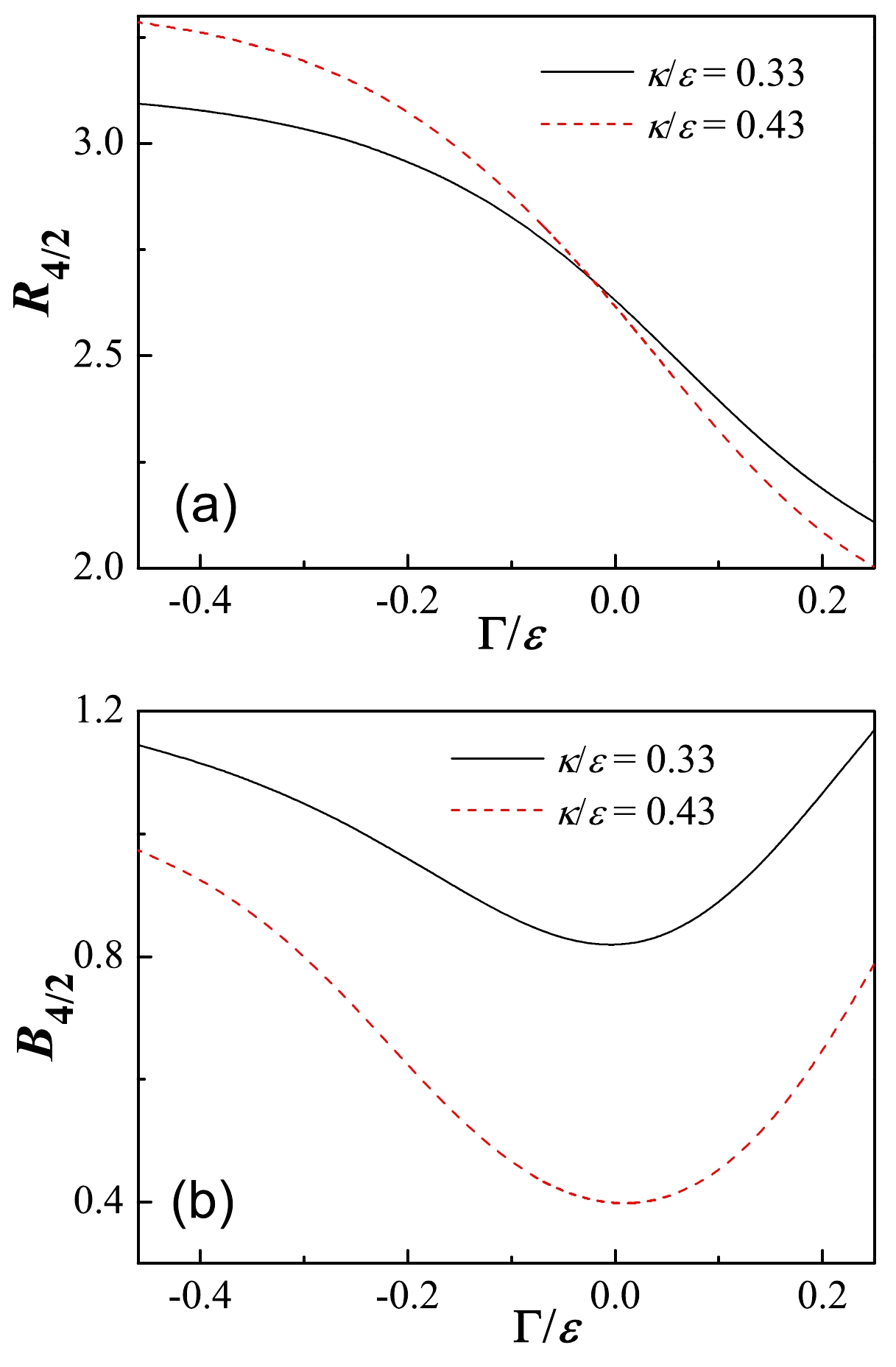
Figure 4. (color online) (a) Energy ratio
$ R_{4/2} $ solved from the Hamiltonian (11) presented as a function of$ \Gamma/\varepsilon $ for two values of$ \kappa/\varepsilon $ . (b) Same as in (a) but for the ratio$ B_{4/2} $ . In the calculations, the boson number was fixed as$ N=8 $ , and the dimensionless parameters$ (a,b,c) $ were chosen to be consistent with those used in Fig. 3. For simplicity and to facilitate comparison, we denote$ R_{4/2}=E(21/2^+)/ $ $ E(17/2^+) $ and$B_{4/2}= $ $ B(E2;21/2^+\rightarrow17/2^+)/B(E2;17/2^+\rightarrow13/2^+)$ .Energy $ ^{169} $ Os

Model $ ^{171} $ Os

Model $ E(13/2_1^+) $ 

0.0 0.0 0.0 0.0 $ E(17/2_1^+) $ 

0.280 0.292 0.254 0.251 (0.244 $ ^\mathrm{a} $ )

$ E(21/2_1^+) $ 

0.758 0.820 0.701 0.740 (0.679 $ ^\mathrm{a} $ )

$ E(25/2_1^+) $ 

1.369 1.344 1.268 1.193 (1.219 $ ^\mathrm{a} $ )

$ E(29/2_1^+) $ 

2.072 2.055 1.896 1.748 (1.878 $ ^\mathrm{a} $ )

$ E(33/2_1^+) $ 

− 3.259 2.540 2.632 (2.734 $ ^\mathrm{a} $ )

$ L_i\rightarrow L_f $ 

$ ^{169} $ Os

Model $ ^{171} $ Os

Model $ 17/2_1^+\rightarrow13/2_1^+ $ 

100 100 100 100 $ 21/2_1^+\rightarrow17/2_1^+ $ 

79 $ _{-20}^{+27} $ 

69 96 $ _{-19}^{+23} $ 

76 (113 $ ^\mathrm{a} $ )

$ 25/2_1^+\rightarrow21/2_1^+ $ 

− 41 128 $ _{-52}^{+62} $ 

33 (101 $ ^\mathrm{a} $ )

$ 29/2_1^+\rightarrow25/2_1^+ $ 

− 30 101 $ _{-29}^{+34} $ 

28 (90 $ ^\mathrm{a} $ )

Table 2. Energy levels (in MeV) and
$ B(E2) $ transitions for the yrast states in$ ^{169,171} $ Os [9] built on$ \nu{i_{13/2}} $ compared with the model calculations (see text for the parameter details). All the$ B(E2;L_i^\pi\rightarrow L_f^\pi) $ values have been normalized to$B(E2;17/2_1^+ $ $ \rightarrow13/2_1^+)=100$ , where "-" indicates unknown data, and the superscript "a" means that the corresponding values are obtained from new parameters.It can be seen from Fig. 5 that both the
$ R_{4/2} $ and$ B_{4/2} $ ratios as a function of the mass number A exhibit evidently odd-even staggering. This demonstrates that the anomalous$ E2 $ structure in the odd-even systems will be influenced by the appearance of odd particles. Encouragingly, all these features can be qualitatively well explained from the model calculations. One can thus conclude that the$ B(E2) $ anomaly features in the odd and even Os systems, as well as their dynamical correlations, may be understood in a unified manner within the proposed algebraic model.
Figure 5. (color online) Evolution of
$ R_{4/2} $ and$ B_{4/2} $ in$ ^{168,169,170,171} $ Os presented as a function of the mass number A for comparison with the model results. The red star represents the value obtained from a new calculation with parameters slightly refined to better reproduce the spectrum of$ ^{171} $ Os (denoted with superscript "a" in Table 2). -
In summary, an algebraic scheme that can treat different collective modes on an equal footing was proposed to examine the
$ E2 $ anomalous structures, as observed in neutron-deficient nuclei. Based on the mean-field analysis and realistic calculations, it was revealed that unusually low values of the$ B_{4/2} $ ratio can emerge from the present model describing the mixing of triaxial rotor and other collective modes. It was further demonstrated that the low-lying levels and anomalous$ E2 $ features with$ B_{4/2}<1.0 $ in$ ^{168,169,170,171} $ Os [6, 8, 9] can be well reproduced by the model calculations, offering a unified explanation of the$ B(E2) $ anomaly structures in the Os nuclei with both even- and odd-mass numbers. It can be said that the present analysis has extended the conventional IBM description of collective modes and uncovered novel features related to triaxiality. The obtained results provide a crosscheck of the triaxial condition in explaining$ B(E2) $ anomalies previously proposed based on the$S U$ (3) schemes [22]. Nonetheless, further experimental measurements, especially on the low-lying non-yrast states in neutron-deficient nuclei, are still needed to confirm the current model explanation of$ B(E2) $ anomalies. -
Discussions with F. Pan and T. Wang on triaxial rotor modes are acknowledged, Chong Qi Thanks KTH for the financial support of his sabbatical leave and Liaoning Normal University for her hospitality during his stay when part of the work was done.
A novel approach for the anomalous collectivity in neutron-deficient Os isotopes
- Received Date: 2024-08-04
- Available Online: 2025-01-15
Abstract: An algebraic model with three-body boson interactions is proposed to incorporate the different quadrupole modes in nuclear collectivity. It is shown that the recently observed anomalous collective structure characterized by





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: