-
The basic assumption of nuclear structure is that nuclei with magic numbers are spherical [1−3]. When the number of valence nucleons increases, spherical vibrational excitation seems to appear inevitably for an even-even nucleus where the residual two-body interaction should appear [2]. This excitation exhibits a nearly equidistant spectrum created by the quadrupole phonon. At the two-phonon excitation level, there are three degenerate states with angular momentum
$ L=4,2,0 $ , whereas at the three-phonon level, there are five degenerate states with$ L=6,4,3,2,0 $ [4].The interacting boson model (IBM) provides a simple but effective method of studying the collectivity in nuclei [5−7]. Recently the extended interacting boson model with SU(3) higher-order interactions (SU3-IBM) was proposed [8], and one spherical-like γ-soft rotation was found in this model to explain the Cd puzzle [4, 9, 10]. The energy of the
$ 0_{3}^{+} $ state is nearly twice that of the$ 0_{2}^{+} $ state; hence, it does not appear near the$ 6^{+},4^{+},3^{+},2^{+} $ states. The$ 0_{3}^{+} $ state is expelled to a higher level (see the bottom graph of Fig. 2 in Ref. [11]).This new model can be considered an IBM realization of the SU(3) symmetry viewpoints adopted in the SU(3) shell models [12−20], some of which have been discussed with pseudo-SU(3) symmetry [21, 22]. Recently, proxy-SU(3) symmetry was found by Bonatsos et al. [23, 24], who investigated the prolate-oblate shape phase transition within only SU(3) symmetry. Higher-order interactions are needed in the IBM [25] to include triaxiality [26, 27]. SU(3) higher-order interactions are related to SU(3) mapping of the rigid triaxial rotor [28−30], which have been investigated to release the degeneracy of the β- and γ-bands in the SU(3) limit [31] and realize the rigid triaxial rotor [32, 33].
The spherical-like spectra in the Cd puzzle [4, 9, 10] have only been found in this SU3-IBM [8]. The B(E2) anomaly can only be explained by the SU3-IBM [34−36], which can not be described by other nuclear theories [37−40] or O(6) symmetry [41]. The prolate-oblate shape phase transition was also found to evolve with an asymmetric way in this model, which is more consistent with the evolution of actual nuclei in the Hf-Hg region [42]. This model can also explain the energy spectra of
$ ^{196} $ Pt at a better level [11, 43] as well as$ ^{82} $ Kr [44]. The SU3-IBM describes the oblate shape with the SU(3) third-order Casimir operator [45, 46], which predicts a boson number odd-even effect [46]. This effect was recently found in$ ^{196-204} $ Hg, which conclusively proves the validity of this new model [47].Recently, Otsuka et al. argued that nuclei previously thought to be prolate ellipsoid, such as
$ ^{166} $ Er, are actually of a triaxial shape [1, 48−50]. This result is attractive and supports the SU3-IBM because it can easily handle triaxial deformations.It is necessary to further investigate the Cd puzzle [4, 9, 10] using the SU3-IBM. In a previous paper [8], only the SU(3) second-order and third-order Casimir operators were considered. In this study, we further investigate other higher-order interactions to explain the near zero B(E2) values between the
$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states. The coupling strength between the normal and intruder states in$ ^{108-116} $ Cd is weak [51]. However, for$ ^{118,120} $ Cd, we find that the coupling between the normal and intruder states can be ignored. Thus, the spectra in$ ^{118,120} $ Cd can be explained without the calculation of configuration mixing (see Table 1). Similar spherical-like spectra may also be found in Pd nuclei [52, 53]. Finally, for the first time, the anomalous evolutional behavior of the quadrupole moments of the$ 2_{1}^{+} $ state in$ ^{108-116} $ Cd can be discussed via the theory, implying that the discussions are meaningful.Cd nuclei Coupling strength Configuration mixing $ ^{108-116} $ Cd

weak needed $ ^{118,120} $ Cd

ignored no Table 1. Main viewpoints adopted in this study.
The Cd puzzle has also been studied from other perspectives [54−57], in which the normal states of Cd nuclei were not regarded as a new collective mode. The properties of Cd nuclei were also discussed in [58, 59], which provides a reasonable qualitative description of the experimental energy levels and transition rates.
-
The Cd puzzle is a challenge discovered in nuclear structure physics [9, 10]. Because a similar phenomenon has also been found in other nuclei, such as Te and Pd [4], it is referred to as the spherical nucleus puzzle in this paper [8]. It was established long ago that shape coexistence [9, 60−62] exists in Cd isotopes [63, 64]. It was also found that the electromagnetic transitions among the normal states are different from the phonon excitation modes. To explain this inconsistency, researchers hypothesized that the coupling between the normal and intruder states is strong by considering Cd nuclei to be spherical [65−67].
However, new experiments do not support this strong coupling viewpoint [68, 69]. The coupling strength was found to be weak [51], which has caused considerable confusion. If the coupling is weak, the normal states are not evidence of a spherical nucleus (the Cd puzzle), and from the electromagnetic transitions, it is more a γ-soft rotor [51]. Thus, the experimental data revealed a new spherical-like γ-soft rotational mode.
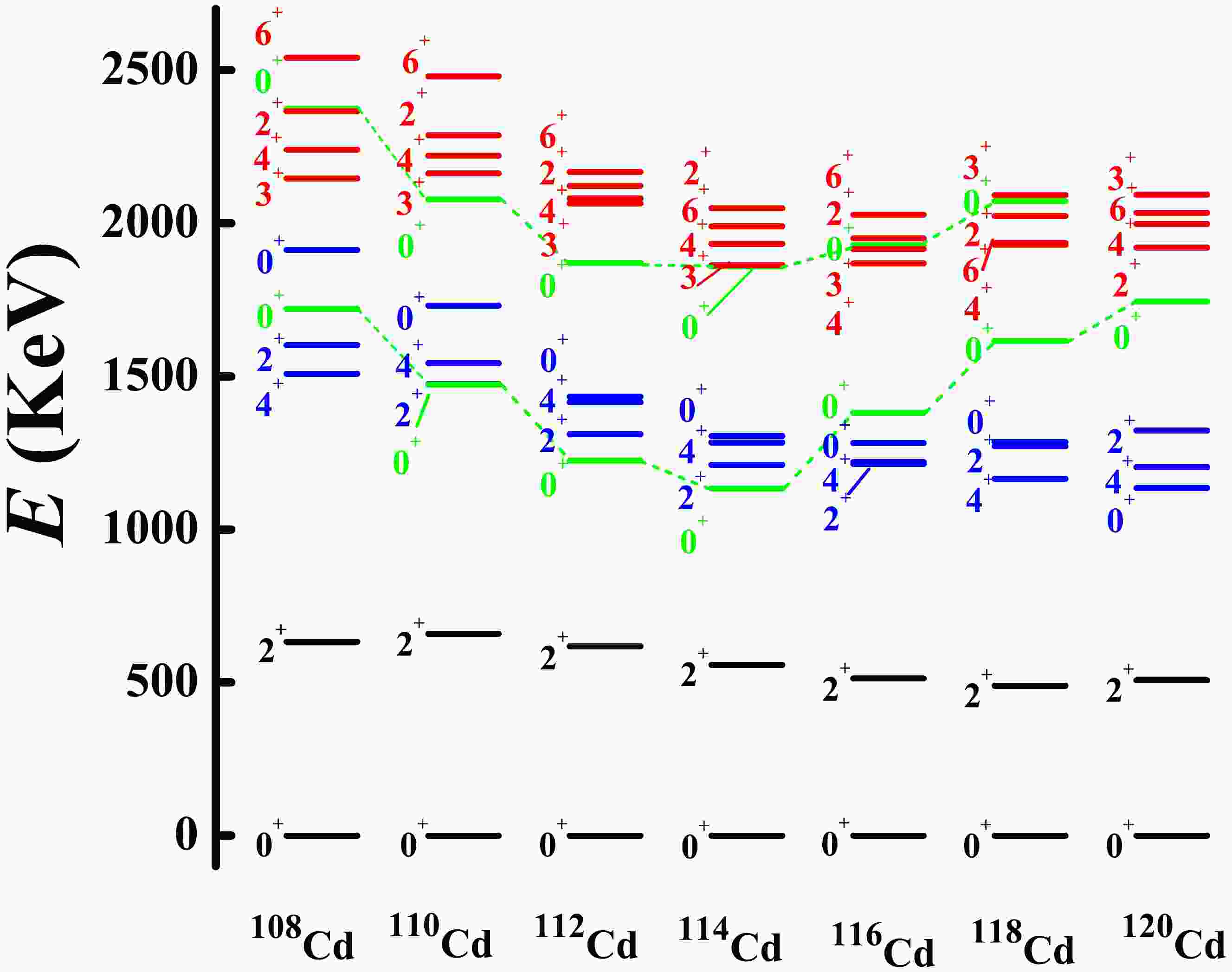
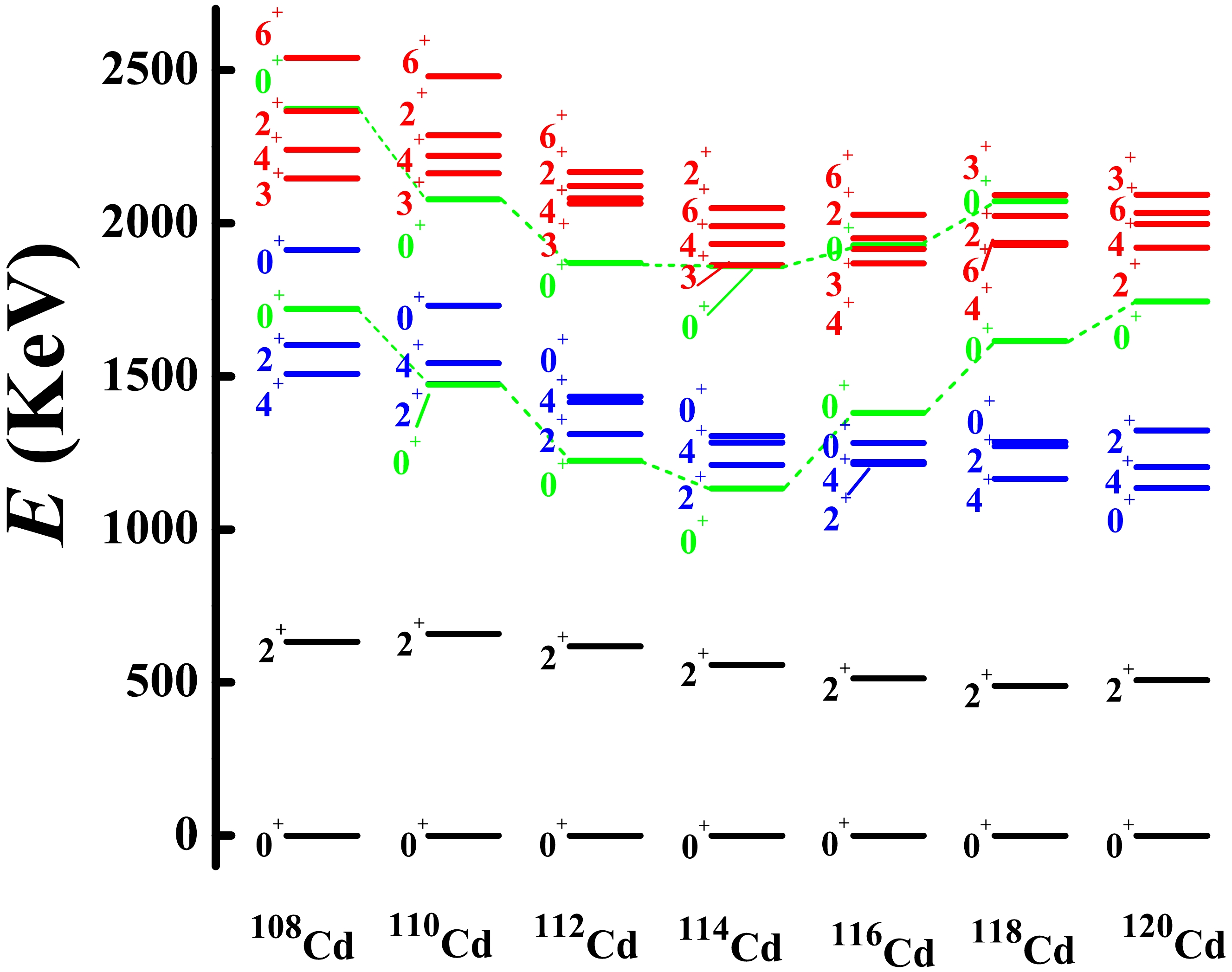
In Ref. [70], it was experimentally found that
$ ^{120} $ Cd has no$ 0_{3}^{+} $ state near the three-phonon level (see Fig. 1 (a)). The$ 0_{3}^{+} $ state is the bandhead of the first intruder states (red band); therefore, for the normal states, the$ 0^{+} $ state at the three-phonon level disappears, and the four states with$ L=6^{+},4^{+},3^{+},2^{+} $ remain. This feature can also be confirmed in$ ^{112} $ Cd experimentally [54, 55] (see Fig. 1 (b)). The$ 0^{+} $ state (blue band) at the three-phonon level was verified as the bandhead of the second intruder states. Thus, at the three-phonon level in$ ^{112} $ Cd, the$ 0^{+} $ state does not exist at all. The normal states in Cd nuclei are, in fact, those indicated in black in Fig. 1.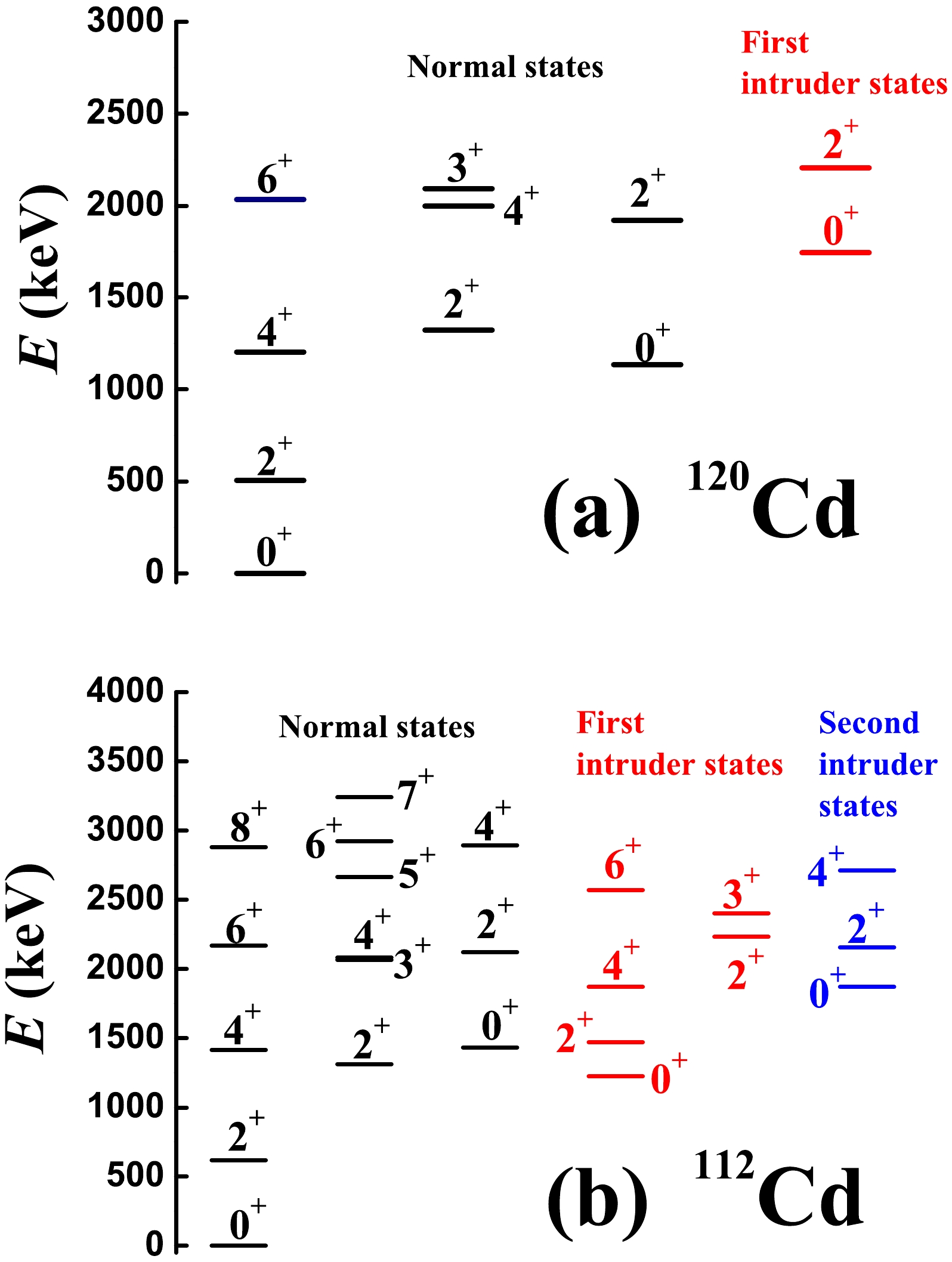
Figure 1. (color online) Partial experimental low-lying spectra for (a)
$ ^{120} $ Cd and (b)$ ^{112} $ Cd. The key observation is that there is no$ 0^{+} $ state at the three-phonon level.More importantly, the two
$ 0^{+} $ states (green color) in the evolution of$ ^{^{108-120}} $ Cd appear to have obvious parabolic shapes (see the experimental systematics in Fig. 2). This is a typical feature of shape coexistence [9, 60−62]. Evidently, the$ 6^{+},4^{+},3^{+},2^{+} $ states evolve in a different manner from the$ 0_{3}^{+} $ state. As shown in Fig. 2, the$ 0^{+} $ state (blue color) evolves in the same manner as the$ 4_{1}^{+}, 2_{2}^{+} $ states and does not exhibit the parabolic feature. Thus, the normal states exhibit a new spherical-like γ-soft spectrum, with a γ-soft rotor, but not an O(6) nucleus. There are two key differences: (1) there is a$ 0_{2}^{+} $ state near the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states (spherical-like), and (2) there is a$ 2_{3}^{+} $ state near the$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ , and$ 3_{1}^{+} $ states, and no$ 0_{3}^{+} $ state.There is a key point to be stressed here (see Fig. 3). From
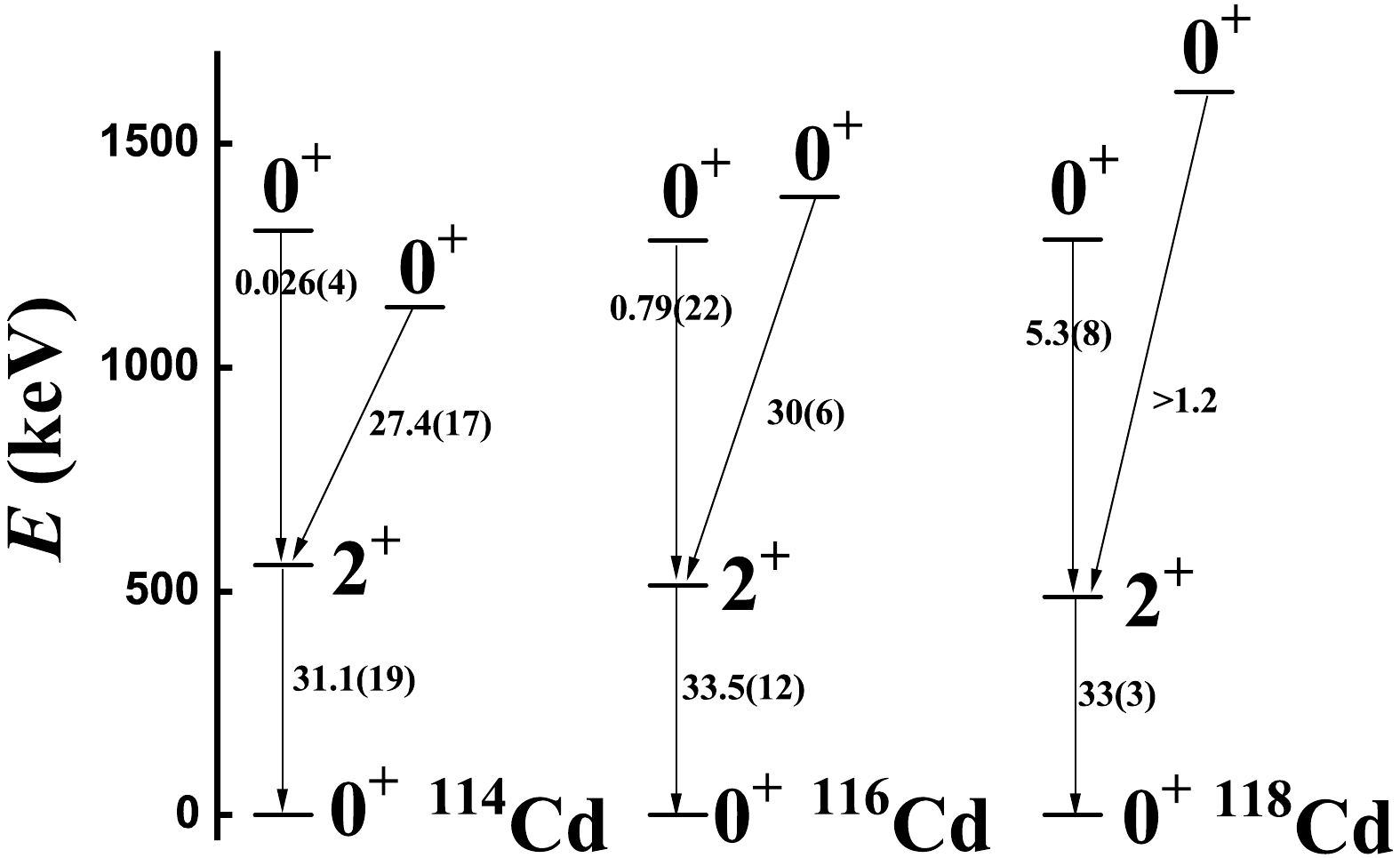
$ ^{114,116} $ Cd to$ ^{118} $ Cd, the experimental level position of the intruder$ 0^{+} $ state moves up, and for$ ^{118} $ Cd, the coupling between the normal and intruder states can be ignored. As shown in Fig. 3, the B(E2) value between the$ 0^{+} $ and$ 2^{+} $ states in the normal states changes rapidly from nearly zero to around 5.3 W.u., which implies that the near zero B(E2) value in$ ^{114,116} $ Cd is partly induced by configuration mixing. The normal states of$ ^{120} $ Cd are the highest; hence, the coupling can also be ignored (see Fig. 2). Thus, we suggest that the normal states of$ ^{118,120} $ Cd are typical of the new spherical-like γ-soft rotation. -
The Hamiltonian in the SU3-IBM has been discussed in Ref. [8, 34, 35, 42, 44]. In a previous paper, except for the d boson number operator
$ \hat{n}_{d} $ , only the SU(3) second-order and third-order Casimir operators$ -\hat{C}_{2}[SU(3)] $ and$ \hat{C}_{3}[SU(3)] $ were considered to explain the normal states of$ ^{110} $ Cd [8]. When other SU(3) higher-order interactions are added, the Hamiltonian is as follows [11]:$ \begin{aligned}[b] \hat{H}=\;&c\Bigg\{\hat{n}_{d}+\eta\Bigg[-\frac{\hat{C}_{2}[SU(3)]}{2N}+\alpha\frac{\hat{C}_{3}[SU(3)]}{2N^{2}} \\ &+\beta\frac{\hat{C}_{2}^{2}[SU(3)]}{2N^{3}}+\gamma\frac{\Omega}{2N^{2}}+\delta\frac{\Lambda}{2N^{3}}\Bigg]\Bigg\}, \end{aligned} $

(1) where c, η, α, β, γ, and δ are fitting parameters,
$ \hat{Q} $ is the SU(3) quadrupole operator,$ \Omega $ is$ [\hat{L}\times \hat{Q} \times \hat{L}]^{(0)} $ , and$ \Lambda $ is$ [(\hat{L}\times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ . The latter two quantities result from SU(3) mapping of the rigid triaxial rotor [32, 33].$ -\hat{C}_{2}[SU(3)] $ ,$ \hat{C}_{3}[SU(3)] $ , and$ -\hat{C}_{2}^{2}[SU(3)] $ can make any SU(3) irreducible representation$ (\lambda,\mu) $ become the ground state in the SU(3) limit. The study of the SU3-IBM revealed that higher-order interactions are essential for describing the rotor rotation; however, many researchers have ignored them to date. This also makes the IBM useful in understanding some collective behaviors.The two SU(3) Casimir operators are related to the quadrupole second or third-order interactions in the SU(3) limit as follows:
$ \begin{aligned} \hat{C}_{2}[ {{SU(3)}}]=2\hat{Q}\cdot\hat{Q}+\frac{3}{4}\hat{L}\cdot\hat{L}, \end{aligned} $

(2) $ \begin{aligned}[b] \hat{C}_{3}[ {{SU(3)}}]=\;&-\frac{4}{9}\sqrt{35}[\hat{Q}\times\hat{Q}\times\hat{Q}]^{(0)}\\ &-\frac{\sqrt{15}}{2}[\hat{L}\times\hat{Q}\times\hat{L}]^{(0)}. \end{aligned} $

(3) For a given SU(3) irreducible representation
$ (\lambda,\mu) $ , the eigenvalues of the two Casimir operators under the group chain$ U(6) \supset SU(3) \supset O(3) $ are expressed as$ \begin{aligned} \hat{C}_{2}[ {{SU(3)}}]=\lambda^{2}+\mu^{2}+\mu\lambda+3\lambda+3\mu, \end{aligned} $

(4) $ \begin{aligned} \hat{C}_{3}[ {{SU(3)}}]=\frac{1}{9}(\lambda-\mu)(2\lambda+\mu+3)(\lambda+2\mu+3). \end{aligned} $

(5) In a previous paper, only the
$ -\hat{C}_{2}[SU(3)] $ and$ \hat{C}_{3}[SU(3)] $ were considered.$ -\hat{C}_{2}[SU(3)] $ describes the prolate shape, which has been known for many years, and$ \hat{C}_{3}(SU(3)) $ describes the oblate shape, which was only recently taken seriously from Ref. [45]. In Ref. [46], the prolate-oblate shape phase transition from$ -\hat{C}_{2}(SU(3)) $ to$ \hat{C}_{3}[SU(3)] $ was first discussed. Recently, when$ \hat{n}_{d} $ was introduced, the asymmetric shape transition was studied in the Hf-Hg region [42], which provided a solid experimental basis for the validity of the SU3-IBM.In the SU(3) description of the rigid triaxial rotor, the other SU(3) higher-order interactions are requisite [32, 33]. Recently, it was also found that explaining the B(E2) anomaly needs the introduction of other SU(3) higher-order interactions [34−36].
From
$ -\hat{C}_{2}[SU(3)] $ to$ \hat{C}_{3}[SU(3)] $ , there is a degenerate point for the SU(3) irreducible representation$ (\lambda,\mu) $ satisfying the condition$ \lambda+2\mu=2N $ , which is also the shape phase transition point from the prolate shape to the oblate shape. Here, N is the boson number. The degenerate point is at$ \alpha=\dfrac{3N}{2N+3} $ . For the transitional region from the U(5) limit to the SU(3) degenerate point, degeneracy between the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states can be found [8], which is a typical feature of γ-softness. Several other higher levels can also be degenerate. However, the reason for this degeneracy is still unknown. The key finding is that the middle positions of the transition region can exhibit spherical-like spectra for the explanation of the normal states of Cd nuclei.Adding the
$ \hat{C}_{3}(SU(3)) $ interaction has already described the spherical-like mode; however, other SU(3) higher-order interactions are necessary when additional details and configuration mixing are considered. Thus, in this study, the influences of other SU(3) higher-order interactions are investigated at a perturbation level, which are also important for understanding other nuclei with the spherical nucleus puzzle, such as Te and Pd nuclei [4].To better understand various types of γ-softness,
$ B(E2) $ values are also necessary. The method of distinguishing the different types of γ-softness becomes more important in the investigation of realistic nucleus properties. The$ E2 $ operator is defined as$ \begin{aligned} \hat{T}(E2)=e\hat{Q}, \end{aligned} $

(6) where e is the boson effective charge. The evolution of the
$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ ,$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ ,$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ ,$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ , and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ values are discussed for various parameters. -
The case in which other SU(3) higher-order interactions are not considered has been discussed in [8], as shown in Fig. 4. Note that the Hamiltonian here is somewhat different from that in [8], leading to more explicit evolutional behaviors. The boson number is chosen as 7. Obviously, the degeneracy between the
$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states can be found. A similar degenerate phenomenon can also be observed in the$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ , and$ 3_{1}^{+} $ states. The$ 0_{2}^{+} $ state is between the two groups of degenerate levels, and the$ 0_{3}^{+} $ state clearly moves up and can no longer be degenerate with the$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ ,$ 3_{1}^{+} $ , and$ 2_{3}^{+} $ states. Note that the$ 0_{2}^{+} $ state can not be higher than the$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ , and$ 3_{1}^{+} $ states (this conclusion can be obtained by numerical calculation). These level features are very different from those in O(6) symmetry (see Ref. [11]).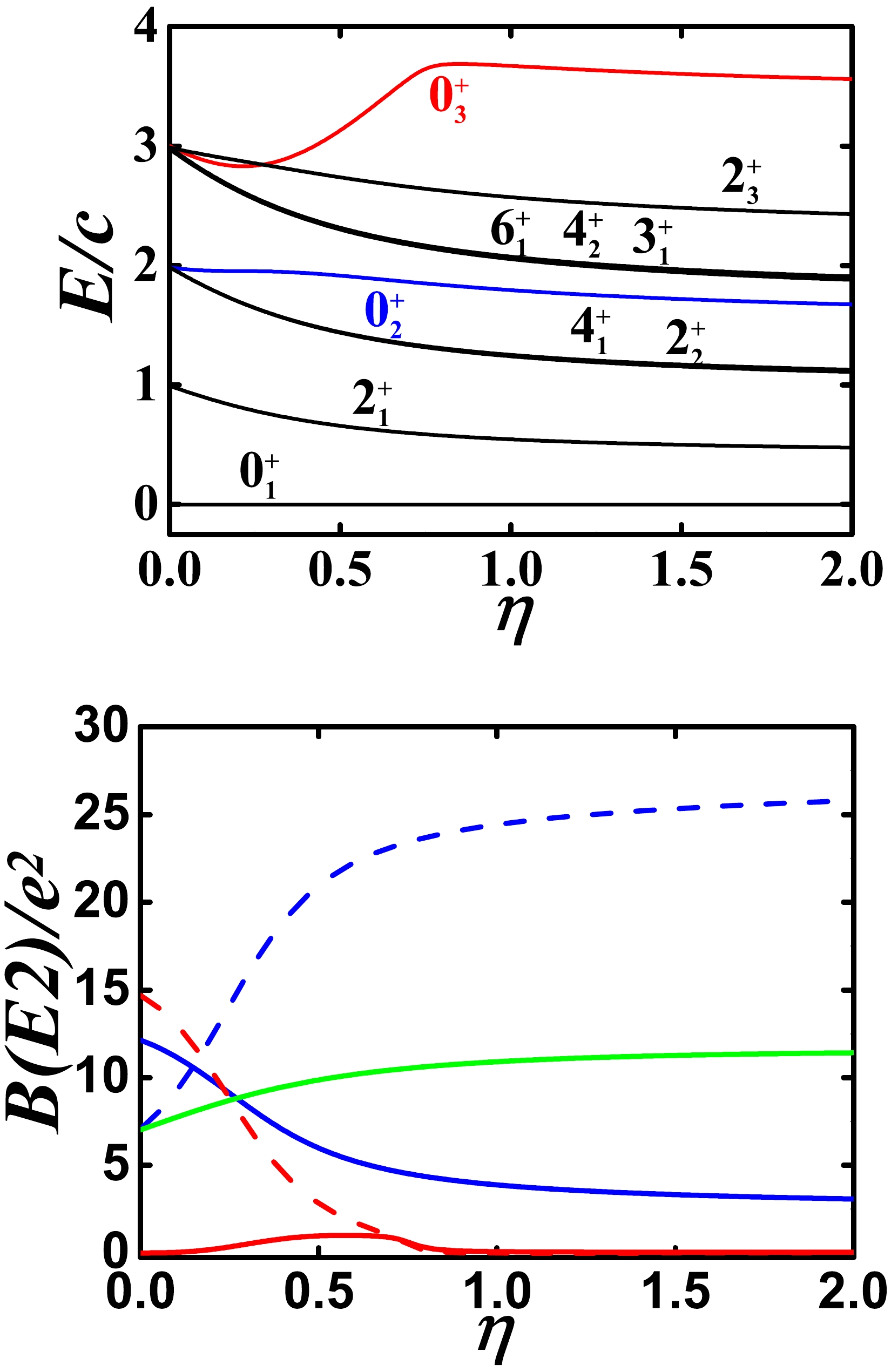
Figure 4. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ and$ \alpha=1.235 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.Although the low-lying levels of the theoretical fitting results and experimental data agree well, the fitting effect of the B(E2) values among the levels is still insufficient in Ref. [8]. In particular, the B(E2) values between the
$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states can be nearly zero in$ ^{112-116} $ Cd. The$ 0_{2}^{+} $ state seems to be nearly degenerate with the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states, which leads to the misunderstanding that the three states constitute the two-phonon triplet states. However, the near zero B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states indicates that the phonon vibration model is impossible. This conclusion may be difficult for many researchers to accept in the field of nuclear structure. In Fig. 4 (bottom graph), it is evident that the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states is considerably smaller than that between the$ 2_{1}^{+} $ and$ 0_{1}^{+} $ states. However, it cannot reach near zero, and to further reduce the B(E2) value, other SU(3) higher-order interactions are needed. Moreover, in Fig. 4, the$ 0_{2}^{+} $ state is closer to the$ 6_{1}^{+} $ ,$ 4_{2}^{+} $ ,$ 3_{1}^{+} $ , and$ 2_{3}^{+} $ states. If the$ 0_{2}^{+} $ state can be brought closer to the$ 4_{1}^{+} $ and$ 2_{2}^{+} $ states, the introduction of the higher-order interactions seems more plausible.Here, we focus on the position
$ \eta=1.0 $ , which shows a typical spherical-like spectrum. For$ \alpha=\frac{3N}{2N+3} $ , this position is the critical point between the prolate shape and rigid triaxial shape [42]. When other SU(3) higher order interactions are introduced at a perturbation level, the quadrupole deformation changes slightly to become more prolate or more oblate.First, the O(3) scalar shift operator
$ \Omega=[\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ is added to the model calculation, as shown in Figs. 5 and 6. The coefficient of this SU(3) third-order interaction in Fig. 5 is 1.0, whereas it is –2.0 in Fig. 6. The negative coefficient greatly reduces the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states, and the degeneracy of the energy levels is broken but varies little.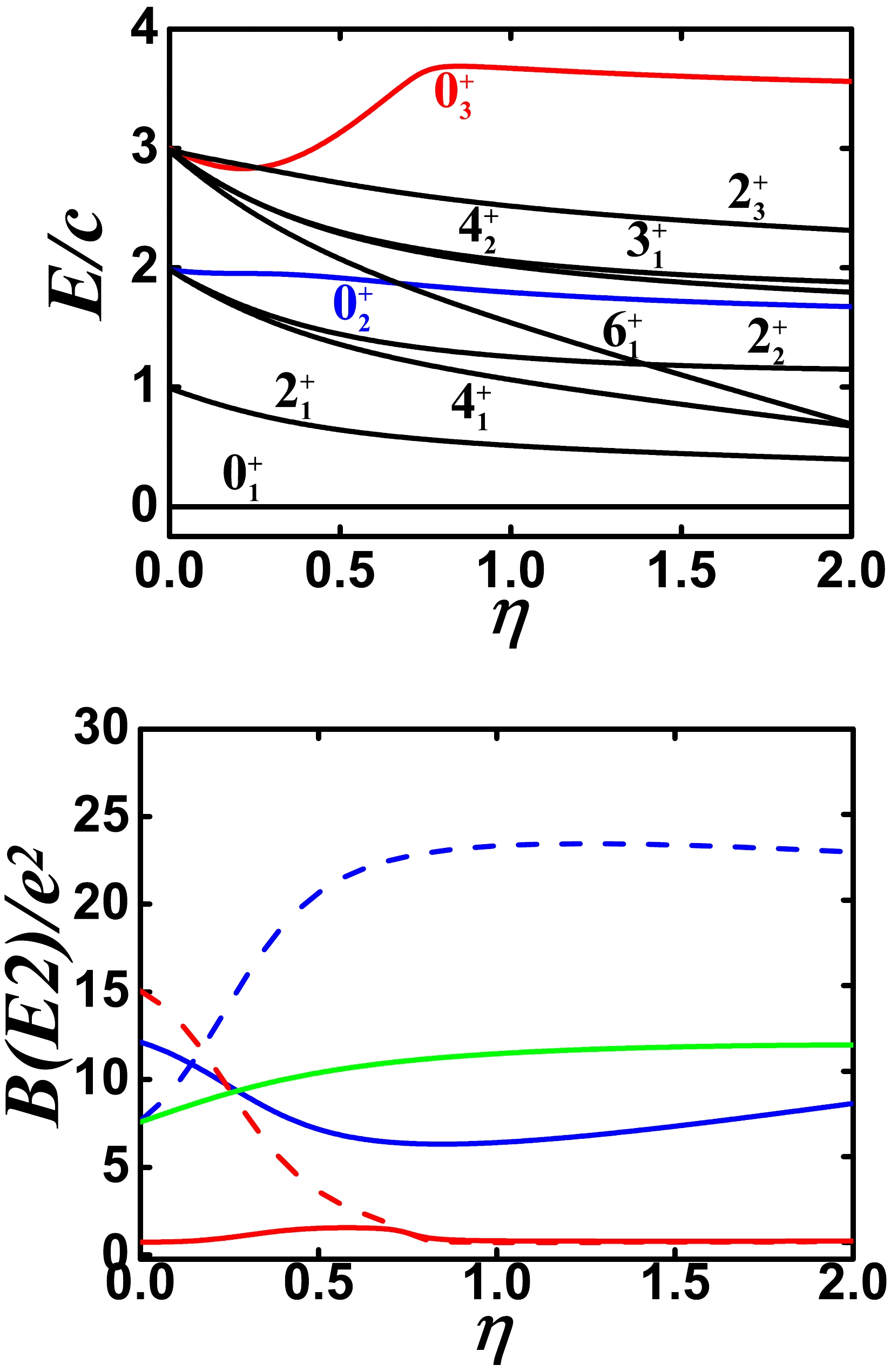
Figure 5. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ , and$ \gamma=1.0 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.
Figure 6. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ , and$ \gamma=-2.0 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.Second, the SU(3) fourth-order interaction
$ [(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ is added to the model calculation, as shown in Figs. 7 and 8. The coefficient is 2.0 in Fig. 7 , whereas it is –4.0 in Fig. 8. The negative coefficient reduces the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states slightly. However, the levels are more like the spectra in the U(5) limit, except for the$ 0_{3}^{+} $ state. This is an important result.
Figure 7. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ , and$ \delta=2.0 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.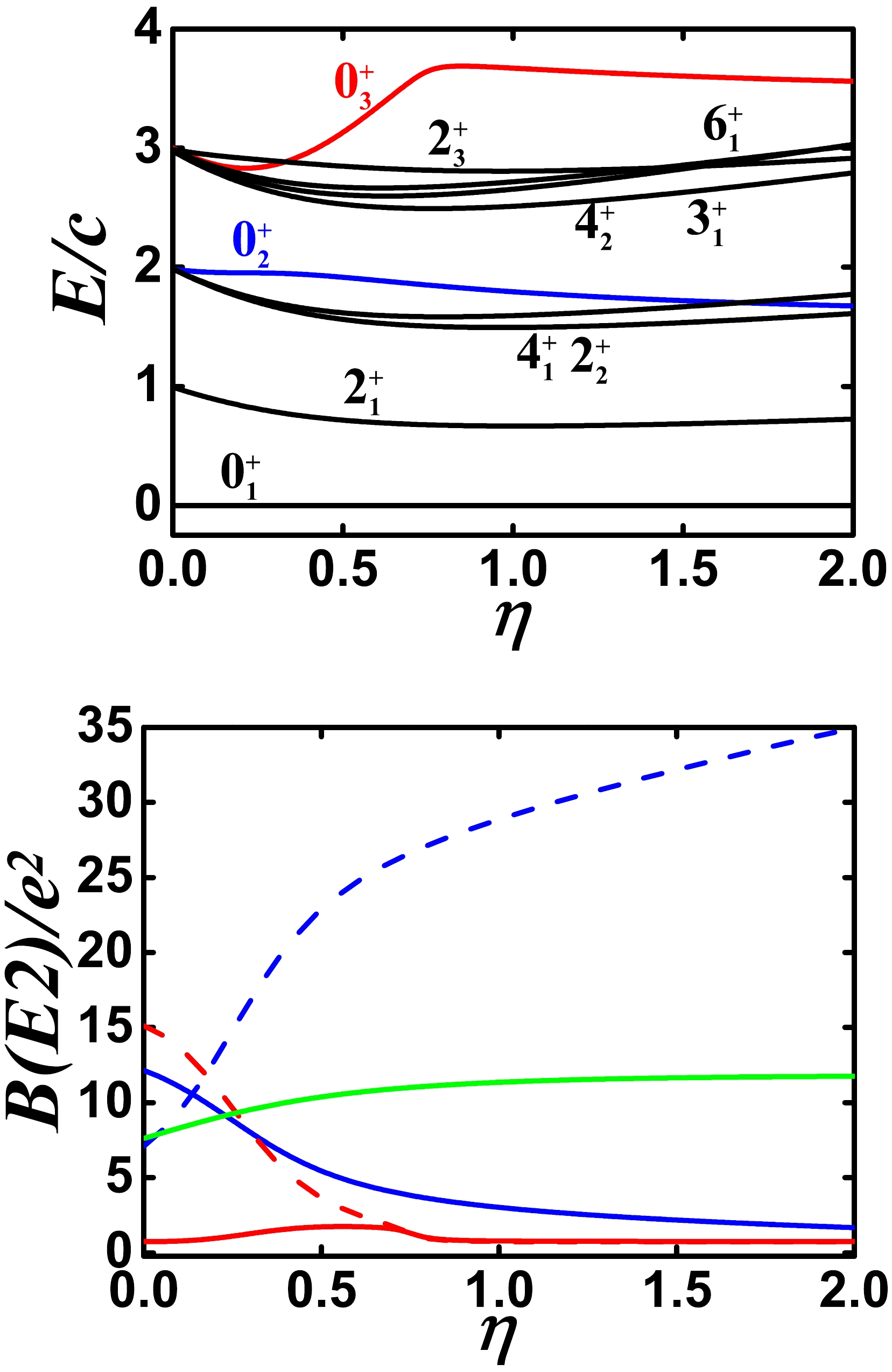
Figure 8. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ , and$ \delta=-4.0 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.Third, the
$ \hat{C}_{2}^{2}[SU(3)] $ is added to the model calculation, as shown in Figs. 9 and 10. The coefficient is 0.03 in Fig. 9 , whereas it is –0.03 in Fig. 10. The positive coefficient reduces the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states, and the degeneracy of the energy levels is broken but also varies little.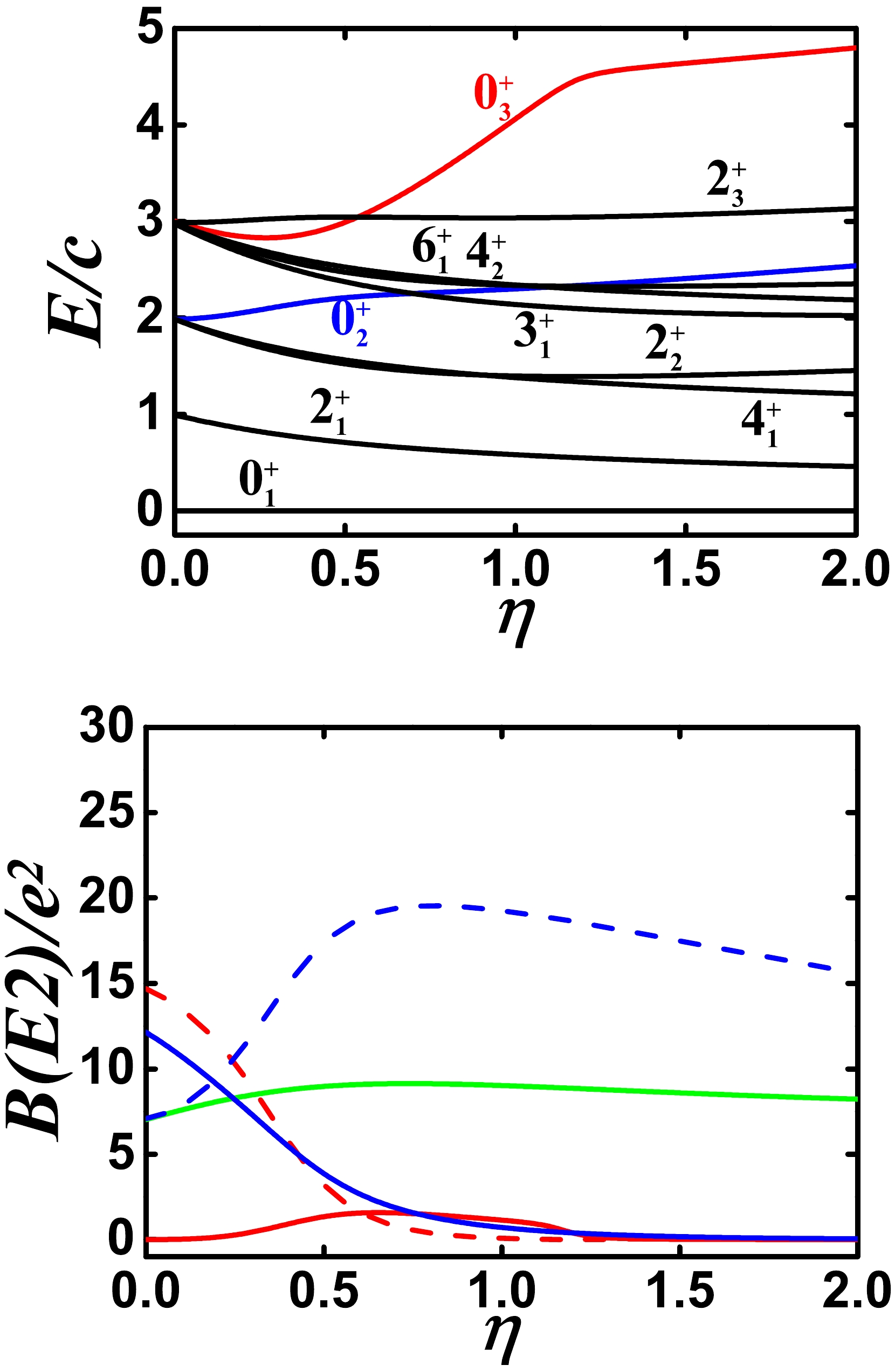
Figure 9. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ , and$ \beta=0.03 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.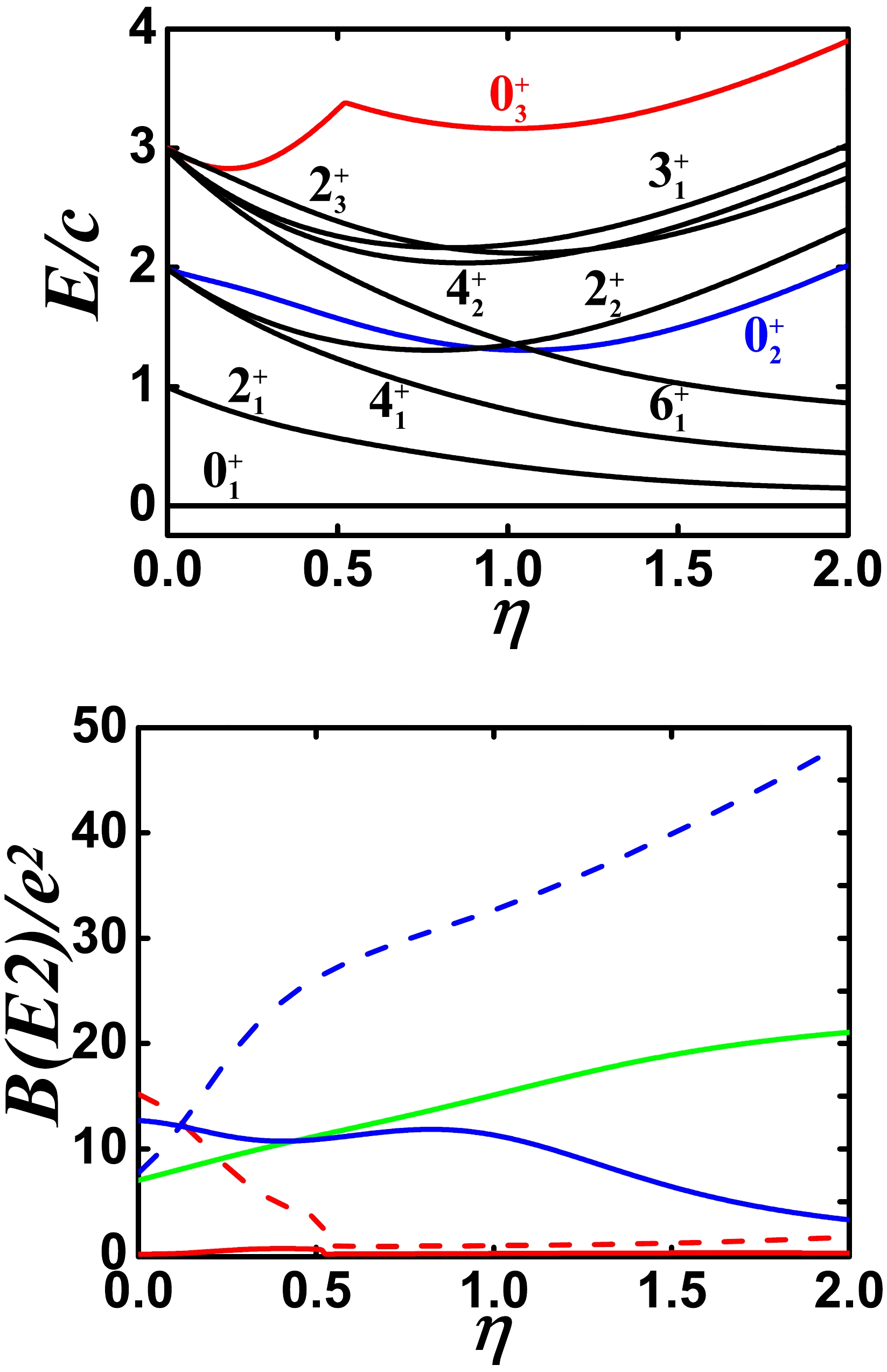
Figure 10. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ , and$ \beta=-0.03 $ (other parameters are zero). Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.Now,
$ \Omega=[\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ and$ [(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ are both added to the model calculation, as shown in Fig. 11. The coefficients of the two are –2.0 and –4.0. The energy spectra are similar to the phonon excitation of a spherical nucleus, except for the$ 0_{3}^{+} $ state, and the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states is small. The spherical-like spectra really exist, which is exactly what we aim to find. Within previous theories, it is difficult to believe that this collective excitation is possible. This reveals that the SU3-IBM is completely self-consistent.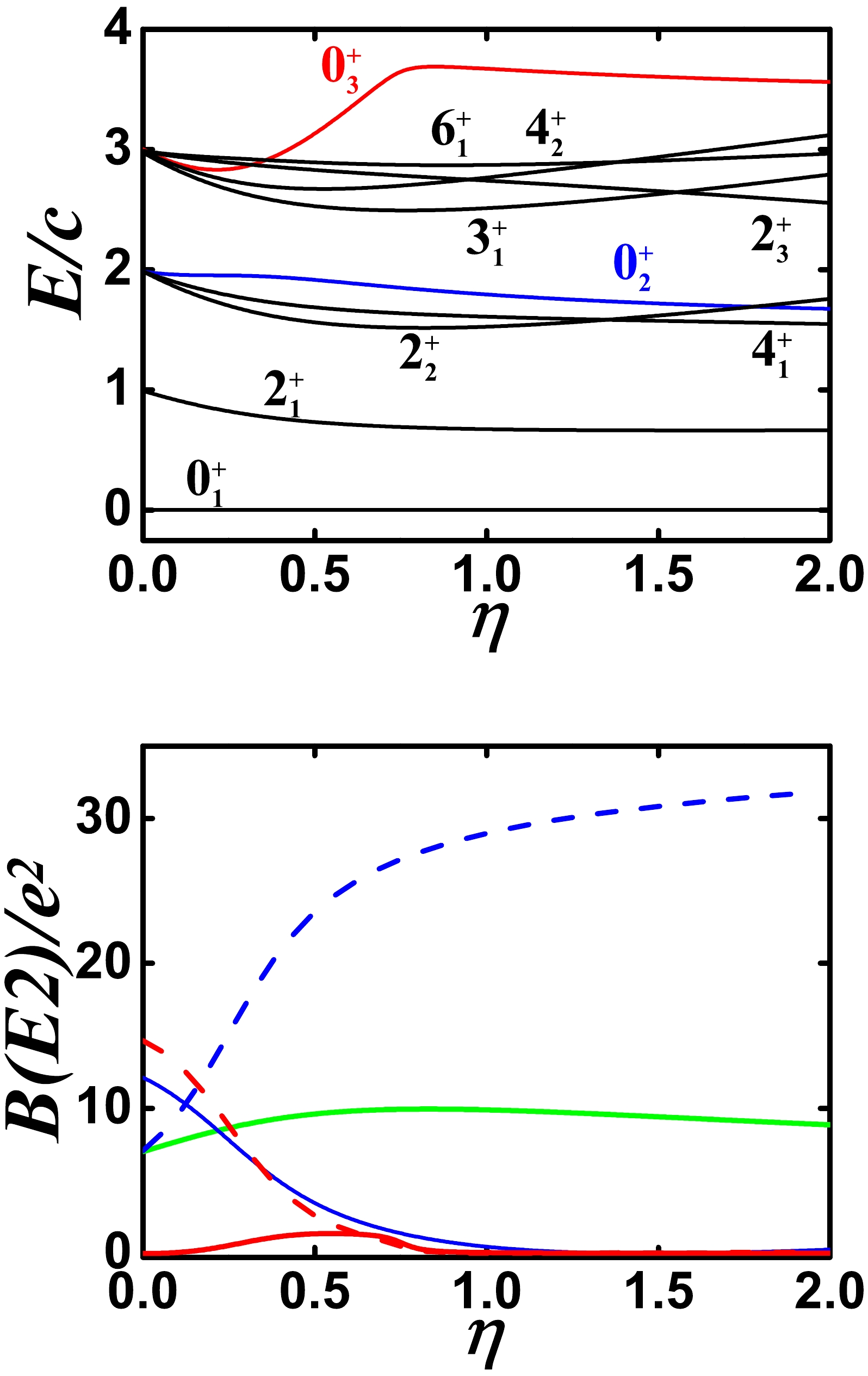
Figure 11. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ ,$ \beta=0 $ ,$ \gamma=-2.0 $ , and$ \delta=-4.0 $ . Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.For completeness, the three higher-order interactions are all added to the model calculation, as shown in Fig. 12 , with the coefficients –2.0, –4.0, and 0.03. The B(E2) value between the
$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states is nearly zero. However, the B(E2) value between the$ 0_{3}^{+} $ and$ 2_{1}^{+} $ states increases.
Figure 12. (color online) Top: Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 2.0 for
$ N=7 $ ,$ \alpha=1.235 $ ,$ \beta=0.03 $ ,$ \gamma=-2.0 $ , and$ \delta=-4.0 $ . Bottom: Evolutional behaviors of$ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line),$ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line),$ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and$ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 2.0 for the same parameters as for the top figure.Finally, the quadrupole moments of the
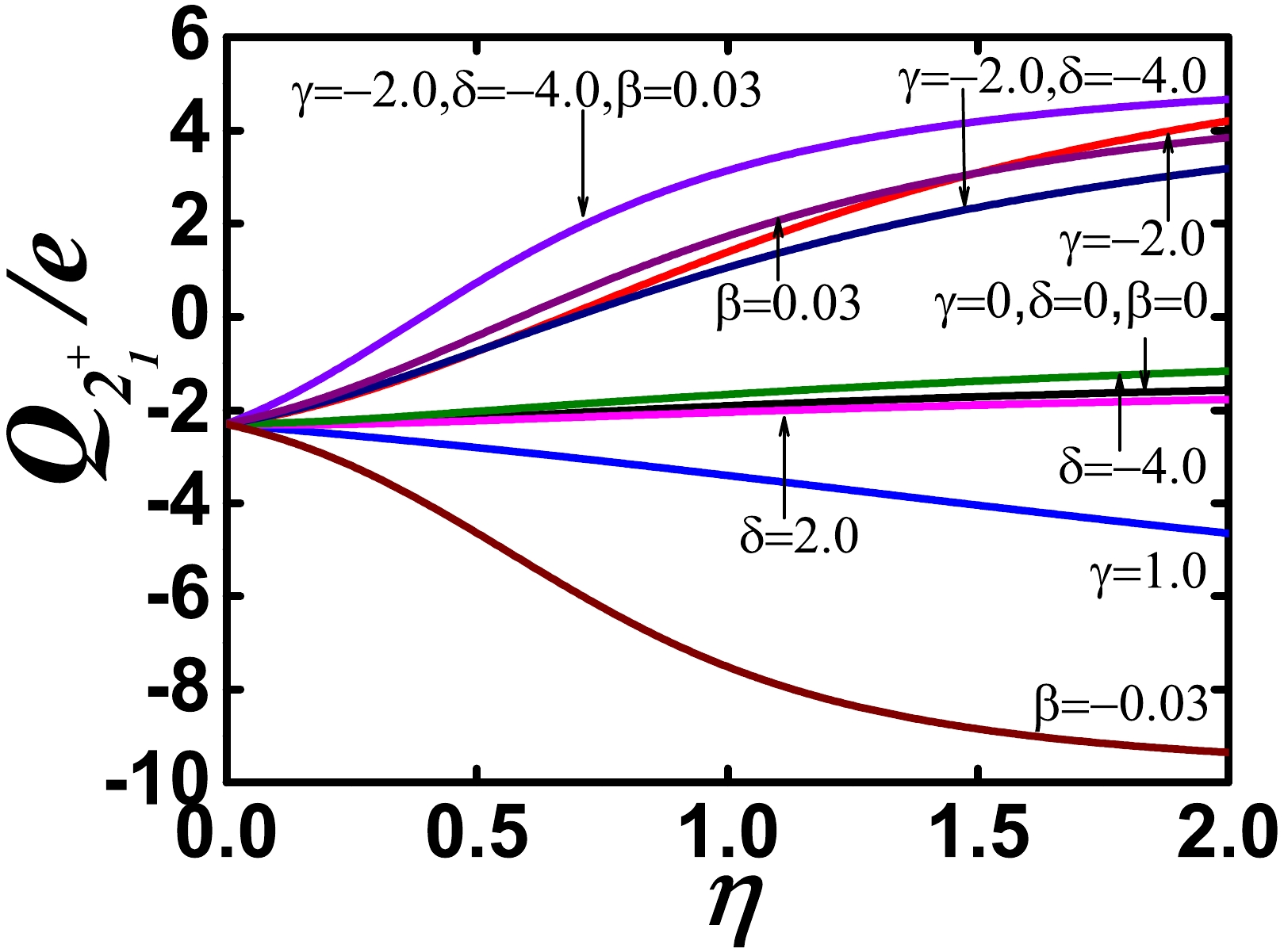
$ 2_{1}^{+} $ state$ Q_{2_{1}^{+}} $ are discussed when various parameters are chosen, as shown in Fig. 13. When other SU(3) higher-order interactions are not considered, the$ Q_{2_{1}^{+}} $ value is approximately -2.0e, which indicates a prolate shape. The$ Q_{2_{1}^{+}} $ value is insensitive to the fourth-order interaction$[(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)}$ (parameter δ), which can induce prominent spherical-like spectra. Thus, this interaction is necessary. The introduction of$ \Omega=[\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ and$ \hat{C}_{2}^{2}[SU(3)] $ can significantly decrease the B(E2) values of the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states; however, this also causes the$ Q_{2_{1}^{+}} $ values to shift to the positive side and the nucleus to become an oblate shape, which conflicts with the experimental results. Thus, these quantities may be needed, but their parameters should not be too large. These findings provide strong constraints for SU(3) higher-order interactions, which will be important for future fitting and configuration mixing calculations. In the latter fitting,$ Q_{2_{1}^{+}} $ plays an important role. Our calculation can reproduce the unique evolution trend of the the quadrupole moments of the$ 2_{1}^{+} $ state$ Q_{2_{1}^{+}} $ in$ ^{108-116} $ Cd, which proves the validity of the conjecture on the spherical-like γ-soft mode. -
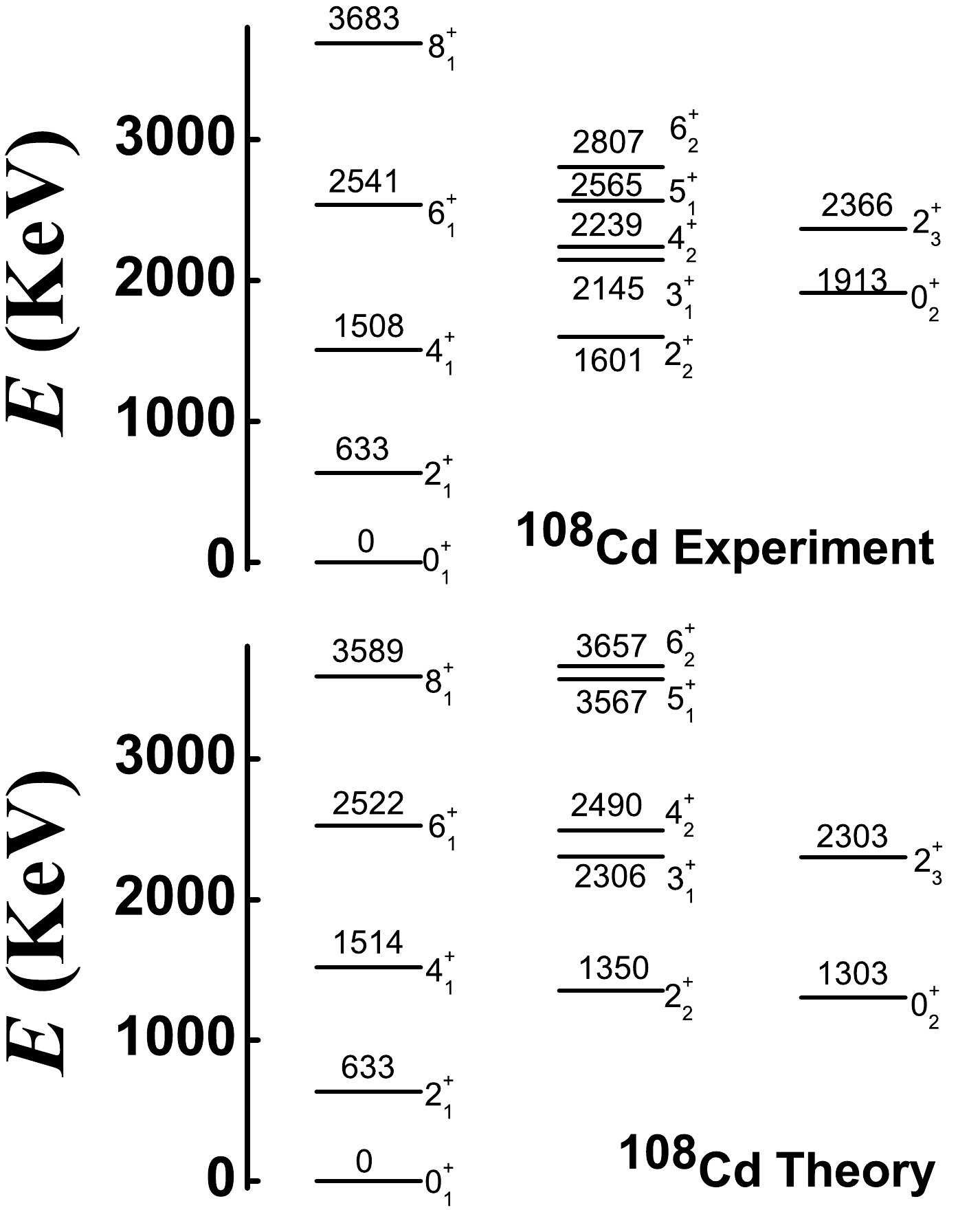
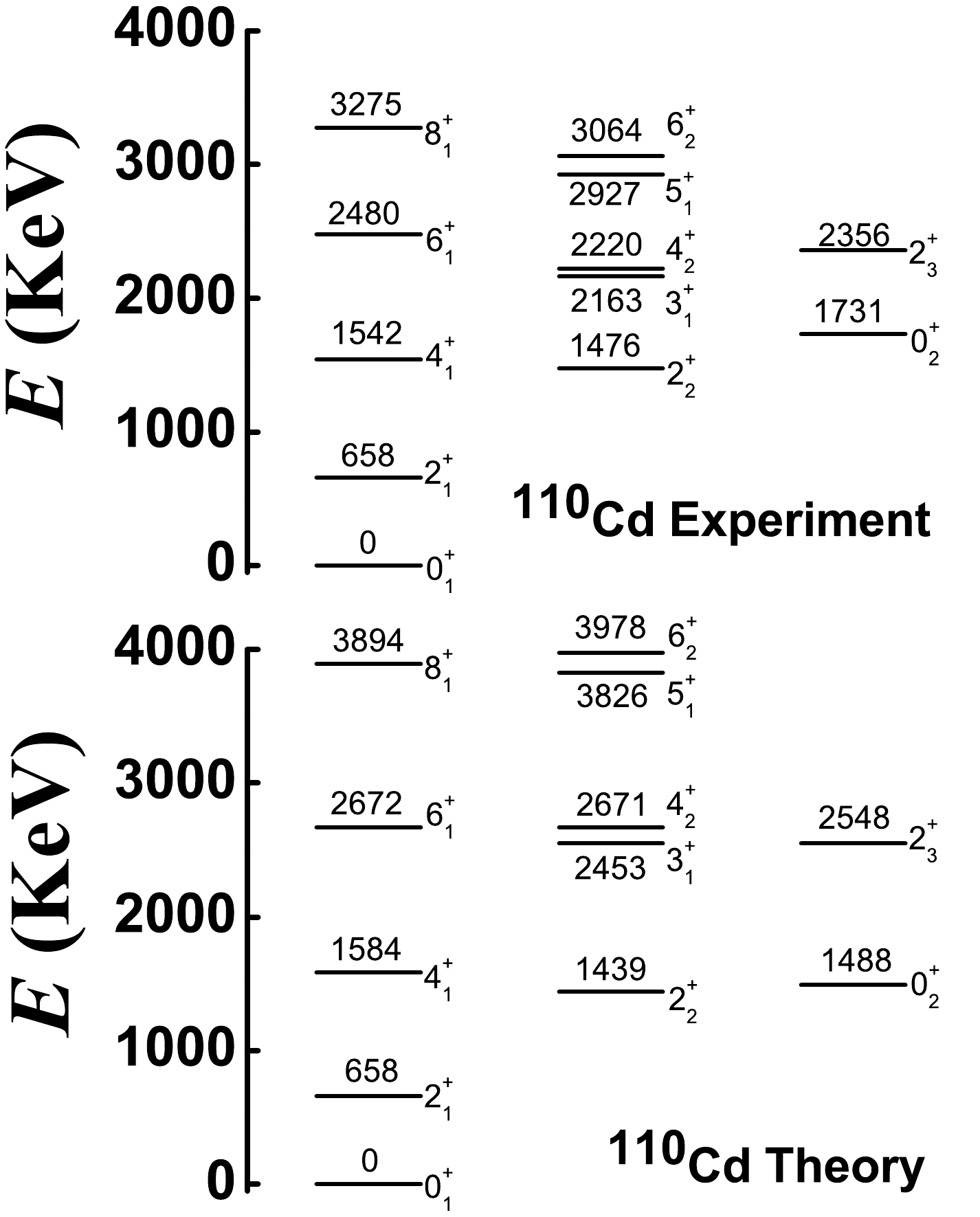
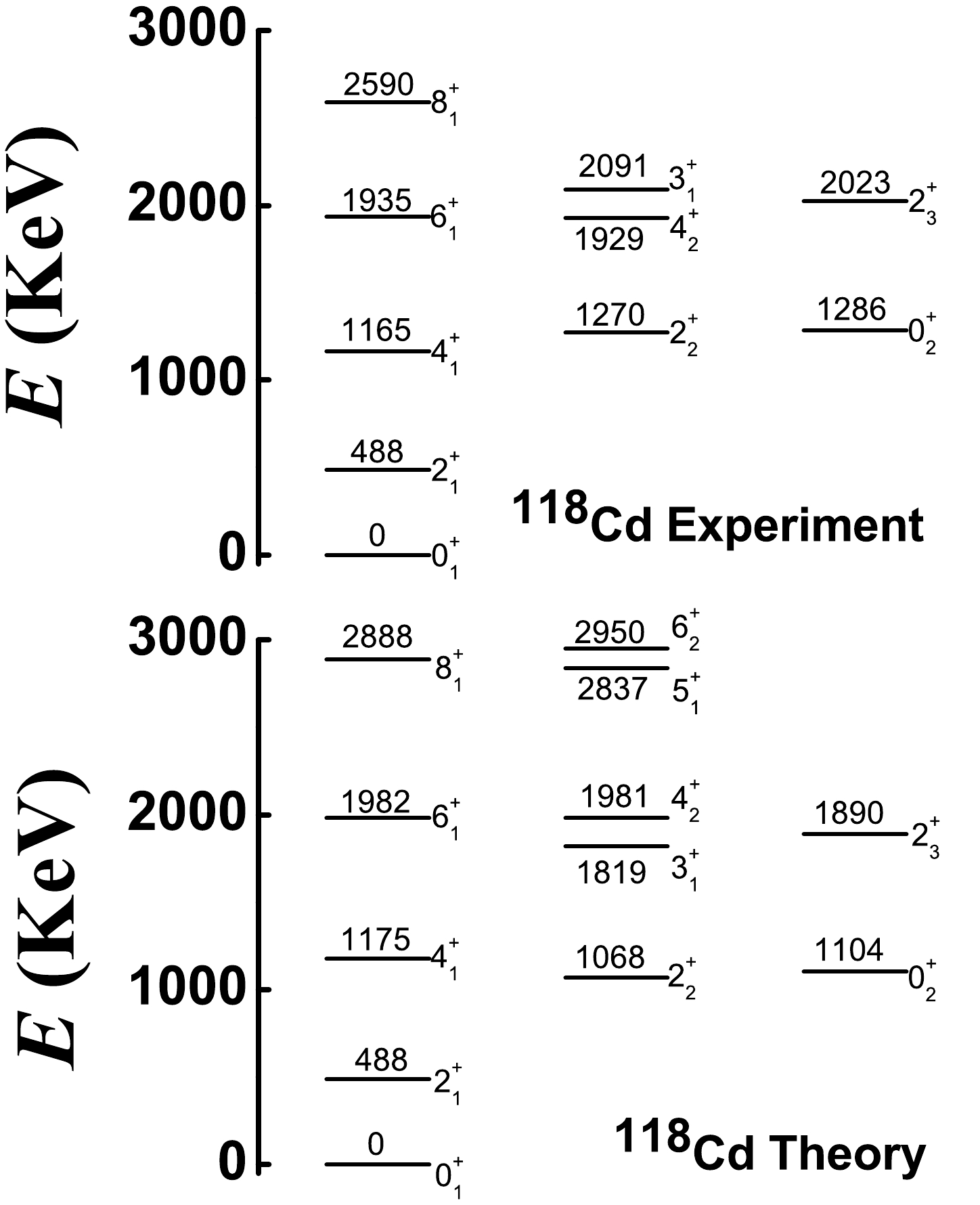
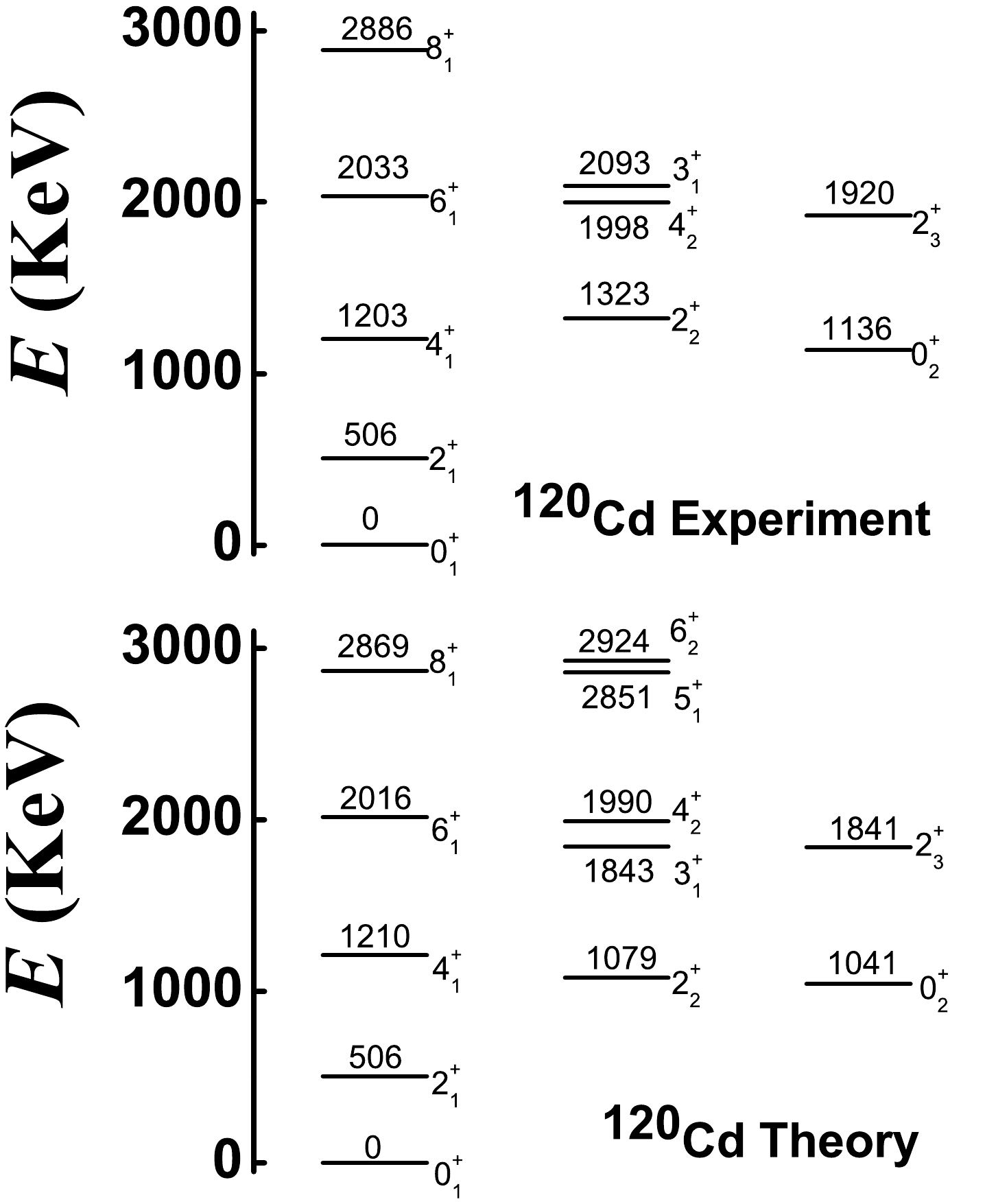
Previous conclusions are used to fit
$ ^{108-120} $ Cd. From Fig. 11, when$ \eta=1.0 $ ,$ \alpha=1.235 $ ,$ \beta=0.0 $ ,$ \gamma=-2.0 $ , and$ \delta=-4.0 $ , we can achieve our aim. As shown, spherical-like spectra clearly exist (top graph), and the B(E2) values from the$ 0_{2}^{+} $ to$ 2_{1}^{+} $ states can be small (bottom graph). However, from Fig. 13, we know that the magnitude of the parameter γ cannot be large. Thus, for all Cd isotopes, we focus on the position$ \eta=1.0 $ and$\alpha={3N}/({2N+3})$ , which is the middle point of the transitional region from the U(5) limit to the SU(3) degenerate point and the typical position of spherical-like spectra [8]. The boson numbers of$ ^{108-120} $ Cd are N = 6, 7, 8, 9, 8, 7, and 6, respectively. It is interesting that the parameters$ \beta=0.0 $ ,$ \gamma=-0.5 $ , and$ \delta=-8.0 $ are also the same for all Cd isotopes. The magnitude of the parameter γ is reduced from –2.0 to –0.5 to ensure the existence of the negative$ Q_{2_{1}^{+}} $ value and reduce the B(E2) values from the$ 0_{2}^{+} $ to$ 2_{1}^{+} $ state. The parameter$ \delta=-8.0 $ reveals spherical-like spectra at a good level, and the$ \hat{C}_{2}^{2}[SU(3)] $ interaction is not needed here. We let the energy of the$ 2_{1}^{+} $ state be the same as the experimental value and choose the fitting parameters c with 688.64, 829.76, 887.39, 902.9, 738.17, 615.38, and 550.48 keV for$ ^{108-120} $ Cd. These results exhibit specific regularity. Figs. 14−20 show the low-lying levels of$ ^{108-120} $ Cd compared with the experimental data [71]. The general features of the energy levels fit well. It should be stressed that there is no$ 0_{3}^{+} $ state at the energy position of the previous three phonon level. The energies of the$ 0_{2}^{+} $ states are somewhat smaller than the experimental values, whereas the high-spin states are somewhat larger. The fitting effect of$ ^{118,120} $ Cd appears to be better than that of the lighter ones because the coupling between the normal and intruder states can be ignored for the two nuclei and the normal states are simply those of the spherical-like γ-soft model.Some deficiencies also require further analysis. It is hoped that the fitting effect can be further improved when configuration mixing is considered in the next study. In this study, a single Hamiltonian is used to fit the entire
$ ^{108-120} $ Cd. This verifies the SU3-IBM but also results in insufficient fitting of some of the levels. We believe that this consequence is justifiable. In further fitting, the parameters will be adjusted more correctly. For$ ^{108-118} $ Cd, the calculated ground-band and γ-band are systematically stretched compared to the observed ones. Considering$ ^{120} $ Cd, this phenomenon is not severe; therefore, we believe that these bands would be more consistent with the experimental results when configuration mixing is considered. We expect this to be confirmed by the latter fitting. Interestingly, the fitting also does not account for the inverted energy levels of the$ 3_{1}^{+} $ and$ 4_{2}^{+} $ states in$ ^{118,120} $ Cd. Note that in$ ^{106} $ Pd, the two levels are normal [52, 53]. The inversion phenomenon will be further discussed in future via careful adjustment of the parameters.The absolute B(E2) values for E2 transitions from the low-lying normal states of
$ ^{108-120} $ Cd are shown in Tables 2−8, revealing that the fitting effects are still good. The key quantity is the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states. In a previous paper [8], without other SU(3) higher-order interactions, this value was 12.2 W.u for$ ^{110} $ Cd, whereas in this study, it is 4.14 W.u.. For$ ^{112,114} $ Cd, these values are nearly zero, whereas for$ ^{116} $ Cd, it is 0.79 W.u. and larger than those of lighter ones. For$ ^{118} $ Cd, the value is 5.3 W.u. (see also Fig. 3). The theoretical fitting result is 5.07 W.u., which fits well (see Table 7). This is the target result of the second paper, and its emergence brings about consistency between theory and experiments. Thus, it can be suggested that the near zero values of$ ^{112,114} $ Cd and the small value of$ ^{116} $ Cd may arise from configuration mixing between the normal and intruder states. This will be discussed in a future paper.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

26.6(3) 26.6 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

41(6) 31.86 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

17(5) 38.89 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

1.8(3) 1.02 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

4.04 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

18.89 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

4.07 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

90.41 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

27.83 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

0.31 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

0.13 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

1.02 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

14.79 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

2.39 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

25.44 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

18.83 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.41 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

20.61 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.026 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.2 $ Q_{2^{+}_{1}} $ 

-0.45 -0.086 Table 2. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{108} $ Cd with effective charge$ e=1.78 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

27.0(8) 27 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

42(9) 33.99 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

30(5) 39.85 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

1.35(20) 0.95 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.7 $ _{-0.6}^{+0.5} $ 

3.55 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

24.2(22) 20.17 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

$ < $ 7.9

4.14 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

$< $ 1680

$ ^{a} $ 

84.05 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

40(30) 35.512 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

$< $ 5

$ ^{a} $ 

0.33 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

$< $ 5

$ ^{a} $ 

0.3 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

2.8 $ _{-1.0}^{+0.6} $ 

0.71 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

12 $ _{-6.0}^{+4.0} $ 

16.13 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.2 $ _{-0.09}^{+0.06} $ 

2.02 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

32 $ _{-14}^{+10} $ 

26.59 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

5.9 $ _{-4.6}^{+1.8} $ 

18.67 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

1.1 $ _{-0.8}^{+1.3} $ 

0.47 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

38 $ _{-24}^{+8} $ 

23.50 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.072 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.13 $ Q_{2^{+}_{1}} $ 

-0.40 -0.076 Table 3. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{110} $ Cd with effective charge$ e=1.59 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

30.31(19) 30.31 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

63(8) 39.47 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

39(7) 45.31 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

0.65(11) 1.166 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

3.42 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

25(7) 23.23 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.0121(17) 4.04 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

99(16) 91.38 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

39.96 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

0.477 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

0.456 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

2.2(6) 0.65 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

24(8) 19.26 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.9(3) 1.85 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

58(17) 30.85 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

25(8) 20.59 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

1.8(5) 0.70 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

64(18) 28.21 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.164 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.093 $ Q_{2^{+}_{1}} $ 

-0.38 -0.045 Table 4. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{112} $ Cd with effective charge$ e=1.53 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

31.1(19) 31.1 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

62(4) 41.39 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

22(6) 44.72 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

0.48(6) 1.72 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

$ < $ 1.9

3.14 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

17 24.51 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.0026(4) 3.65 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

127(16) 89.58 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

119(15) 43.54 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

0.56 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

0.54 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.53 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

20.39 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

1.60 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

31.92 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

20.99 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.88 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

30.72 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.21 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.059 $ Q_{2^{+}_{1}} $ 

-0.35 -0.018 Table 5. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{114} $ Cd with effective charge$ e=1.41 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

33.5(12) 33.5 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

56(14) 43.63 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

25(10) 50.08 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

1.11(18) 1.29 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

3.80 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

25.68 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.79(22) 4.47 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

3.0 $ \times $ 10

$ ^{4} $ (8)

101 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

1.1 $ \times $ 10

$ ^{2} $ 

$ _{-8}^{+4} $ 

44.17 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

0.53 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

0.5 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.72 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

21.28 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

2.04 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

34.07 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

22.76 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.775 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

31.18 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.181 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.103 $ Q_{2^{+}_{1}} $ 

-0.42 -0.049 Table 6. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{116} $ Cd with effective charge$ e=1.61 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

8.37 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

10.02 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

12.23 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

0.32 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

1.27 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

5.94 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

1.28 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

28.43 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

8.75 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

0.01 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

0.04 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.325 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

4.65 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.75 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

80 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

5.92 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.13 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

6.48 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.0083 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.064 $ Q_{2^{+}_{1}} $ 

-0.052 Table 8. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{120} $ Cd with effective charge$ e=1.0 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.B(E2) Exp. Theory B(E2) Exp. Theory 2 $ _{1}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

33(3) 33 4 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

$ > $ 61

41.61 2 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

48.8 2 $ _{2}^{+} $ 

$ \rightarrow $ 0

$ _{1}^{+} $ 

1.16 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

4.35 2 $ _{3}^{+} $ 

$ \rightarrow $ 0

$ _{2}^{+} $ 

24.69 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

5.3(8) 5.07 0 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

102.9 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

39.84 6 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{2}^{+} $ 

0.40 2 $ _{3}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

0.37 2 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.87 4 $ _{2}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

19.75 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

2.49 4 $ _{2}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

32.56 3 $ _{1}^{+} $ 

$ \rightarrow $ 4

$ _{1}^{+} $ 

22.86 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.57 3 $ _{1}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

28.77 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{1}^{+} $ 

0.087 0 $ _{3}^{+} $ 

$ \rightarrow $ 2

$ _{2}^{+} $ 

0.16 $ Q_{2^{+}_{1}} $ 

-0.089 Table 7. Absolute B(E2) values in W.u. for
$ E2 $ transitions from the low-lying normal states of$ ^{118} $ Cd with effective charge$ e=1.76 $ (W.u.)$ ^{1/2} $ . The last row is the$ Q_{2_{1}^{+}} $ value in eb.Note that the theoretical values
$ Q_{2_{1}^{+}} $ in$ ^{108-116} $ Cd are considerably smaller than the experimental data. In the previous analysis, we find that the coupling between the normal and intruder states in$ ^{118,120} $ Cd can be ignored (this is also supported by Ref. [70]). Therefore, the deviation in the$ Q_{2_{1}^{+}} $ values in$ ^{108-116} $ Cd may result from configuration mixing. The first intruder states in$ ^{114} $ Cd are the lowest among all Cd isotopes; hence, their theoretical values$ Q_{2_{1}^{+}} $ have the largest deviation from the experimental value. In this case, the experimental values$ Q_{2_{1}^{+}} $ in$ ^{118,120} $ Cd can be predicted at around –0.09 eb, which is considerably smaller than the values for$ ^{108-116} $ Cd. We strongly suggest that future experiments measure this value and, if this is the case, prove the validity of the SU3-IBM.The top graph of Fig. 21 shows the evolutional behaviors of the
$ Q_{2_{1}^{+}} $ values in Te, Pd, Cd, Ru, and Xe nuclei. Clearly, the evolutional trends in$ ^{108-116} $ Cd are different from the neighbouring ones and decrease as N increases. This is an anomalous phenomenon. (To the best of our knowledge, this anomaly is mentioned for the first time in this paper.) Although these theoretical$ Q_{2_{1}^{+}} $ values are significantly smaller than the experimental values, they reproduce the anomalous trend (see the bottom graph of Fig. 21). The differences arise from configuration mixing. This result indicates that both our hypothesis and results are reasonable.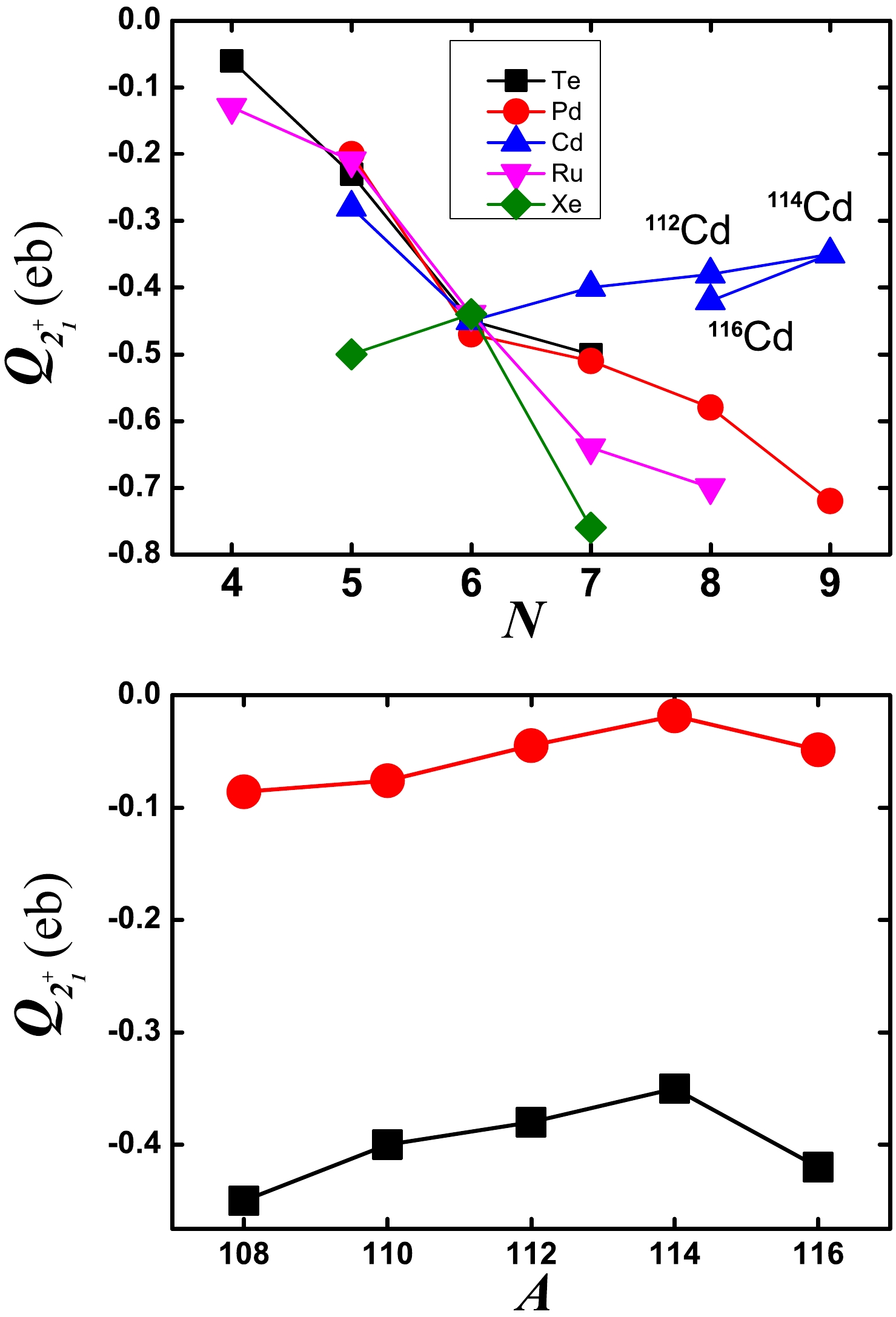
Figure 21. (color online) Top: Evolutional behaviors of the experimental
$ Q_{2_{1}^{+}} $ values in Te, Pd, Cd, Ru, and Xe nuclei [71]. Bottom: Evolutional behaviors of the theoretical (red) and experimental (black) results for$ ^{108-116} $ Cd.The theoretical fitting and practical situation are consistent, and the deficiency originates from not considering configuration mixing. For
$ ^{108-116} $ Cd, the coupling effect, although weak, must be considered, and the resulting deficiency is clear. For$ ^{118,120} $ Cd, the fitting is very reasonable, indicating that the coupling between the normal and intruder states can be ignored. We look forward to more experimental studies on$ ^{118,120} $ Cd.The energy level feature of a nearby nucleus
$ ^{106} $ Pd is found to also possess both of these features. The$ 0_{3}^{+} $ state is found to be an intruder state [52], such that the$ 0_{4}^{+} $ state is in fact the third$ 0^{+} $ state of the normal states [53], and its energy is 1.77 times than that of$ 0_{2}^{+} $ state (see Fig. 6 in Ref.[53]). The energy level feature at the four phonon level in the spherical-like spectra can be verified, which will be discussed in future. In this study, we show that the new spherical-like γ-soft mode can be found in the normal states of$ ^{118,120} $ Cd. -
This is the second paper discussing the Cd puzzle with the SU3-IBM. The first noted that the Cd puzzle implies a new mode of collective motion, which indicates a new possibility for the origin of the collective nature of nuclei. In the SU3-IBM, this mode was found by introducing the SU(3) third-order interaction. In this study, we continue to examine this idea in preparation for further configuration mixing calculations.
The rationality of the theory is further verified from three aspects. First, we fit all
$ ^{108-120} $ Cd using a single Hamiltonian. When the SU(3) higher-order interactions are added, the sphere-like spectra can be described more accurately, which is also the first purpose of this study. Except for some deficiencies, the overall fitting effect of the energy spectra of these isotopes is good at a qualitative level. The fitting results agree with the experimental values, especially for$ ^{118,120} $ Cd. When using only a single Hamiltonian, the change in the spectra of the Cd nuclei depends on the boson number N.The second aspect is the B(E2) values from the
$ 0_{2}^{+} $ to$ 2_{1}^{+} $ state. The purpose of this study is to further reduce this B(E2) value from the results of the first study. The experimental values in$ ^{112,114} $ Cd are nearly zero, which provides a challenge for nuclear structure theories. We find that the theory can explain the B(E2) value in$ ^{118} $ Cd at a good level. The theoretical value is 5.07 W.u., whereas the experimental value is 5.3(8) W.u. This result illustrates that the near zero B(E2) values in$ ^{112,114} $ Cd are due to two reasons. The first is because the value of the spherical-like γ-soft mode itself is relatively small, and the second is configuration mixing. We anticipate further calculations to confirm this.The third and most important aspect is to provide the anomalous evolution trend of the quadrupole moment of the
$ 2_{1}^{+} $ state$ Q_{2_{1}^{+}} $ . This result is especially valuable given that only one Hamiltonian is used and is also an unexpected finding. This anomaly is induced by spherical-like γ-soft rotation. The differences between the experimental and theoretical values arise from configuration mixing, which will be verified in the next study.Based on recent research on
$ ^{196-204} $ Hg [47] and the work in this paper, we find that the fit is sensitive to the boson number N, which confirms the basic assumption of the IBM. Thus, the bosons are highly like nucleon pairs. In the actual case, distinguishing protons and neutrons is important for understanding spherical-like spectra. Therefore, further generalization to the SU3-IBM-2 is needed, and we may find that the Hamiltonian will cause differences between the descriptions of protons and neutrons. This will also help us better understand the evolution of Cd isotopes and further improve the fitting effect.Nuclear energy density functionals are also useful for understanding shape evolution, which have been explored to study the properties of Cd nuclei [58, 59, 72−74]. This approach establishes the connection between nuclear force theory and nuclear structure theory. The SU3-IBM has the potential to further improve our understanding of nuclear forces; therefore, establishing a link between the energy density functional and SU3-IBM is necessary, such as in the works of Nomura et al. [75−78].
Clearly, these new results provide a key step toward completely solving the spherical nucleus puzzle. According to studies on the SU3-IBM [8, 11, 34−36, 42−44, 47] as well as this study, the SU3-IBM is a more plausible model for describing the low-energy excitation behaviors of realistic nuclei. Ref. [8] and this paper stress the Cd puzzle. These studies are even more important because they support denying the existence of spherical nuclei. Although the absence of spherical nuclei has been proposed in Refs. [4, 10, 51, 68, 69], there is no theory to truly support this conclusion, especially in identifying this pattern. In this study, we reveal that the SU3-IBM can offer a reasonable answer and fits well in many aspects.
The SU3-IBM contains two features that are not found in previous nuclear structure theories: higher-order interactions and SU(3) symmetry, which the interactions have except for the pairing one. In this study, we show that the SU(3) second-order and SU(3) third-order interactions both play the same important roles, and other higher-order interactions are also necessary (although small). As we know, the theories of nuclear structure are based on the mean field perspective; therefore, the residual interactions should be governed by two-body interactions. However, the Cd puzzle breaks down with this idea. In our theory, the three-body interaction can play the same role as the two-body interaction. In Refs. [42, 46], the SU(3) third-order interaction even plays a decisive role. These results appear to conflict with the idea of the mean field perspective.
It is clear that the experimental results of the Cd puzzle challenge the mean field perspective, and our results support this challenge. The mean field is present, but for residual interactions, the two-body interactions do not necessarily play the dominant role. Our current understanding of the mean field is inadequate. Recently, Machleidt and Sammarruca raised the following question: "Are the energies typically involved in conventional nuclear structure physics low enough to treat nucleons as structure-less objects?" [79] We conjecture that the Cd puzzle may be related to the medium modifications of the nuclear force [80]. We anticipate more possible studies on this conjecture.
-
Based on a previous study in which the Cd puzzle was referred to as a spherical-like γ-soft rotation, other SU(3) higher-order interactions are used to understand this new γ-soft pattern. The SU(3) fourth-order interaction
$ [(\hat{L} \times \hat{Q})^{(1)} \times (\hat{L} \times \hat{Q})^{(1)}]^{(0)} $ can induce prominent spherical-like spectra, except for the$ 0^{+} $ state at the three phonon level, which is repelled to a higher energy level (at the four phonon level). This quantity also has little effect on the electric quadrupole moment of the$ 2_{1}^{+} $ state. The SU(3) third-order interaction$ \Omega=[\hat{L} \times \hat{Q} \times \hat{L}]^{(0)} $ and the square of SU(3) second-order Casimir operator$ \hat{C}_{2}^{2}[SU(3)] $ can reduce the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states. However, they can also reduce the electric quadrupole moment of the$ 2_{1}^{+} $ state, which poses strict restrictions on the parameters of these two quantities.It is encouraging that a simple set of parameters can be used to fit
$ ^{108-120} $ Cd, especially$ ^{118,120} $ Cd. The coupling between the normal and intruder states in$ ^{118,120} $ Cd can be ignored. This conclusion is also supported by the experimental data, in which the intruder states in$ ^{118,120} $ Cd are higher than those in$ ^{108-116} $ Cd. For$ ^{118} $ Cd, the B(E2) value between the$ 0_{2}^{+} $ and$ 2_{1}^{+} $ states fits well, which is one of the main results of this study.This study predicts that the values of the electric quadrupole moment of the
$ 2_{1}^{+} $ state in$ ^{118,120} $ Cd are approximately –0.09 eb, which requires experimental verification.The normal states in
$ ^{118,120} $ Cd are suggested to be typical examples of spherical-like spectra, and the normal states in$ ^{106} $ Pd and other possible spherical-like spectra will be investigated in future.These reasonable results imply that the assumption of a spherical-like γ-soft rotational mode is reasonable and that the SU3-IBM can be used to explain the spherical nucleus puzzle. The remaining deficiency on the Cd puzzle may arise from configuration mixing, which will be performed in the next study.
Spherical-like spectra for the description of the normal states of 108-120Cd in the SU3-IBM and the $ {{\boldsymbol Q}_{\bf 2_{1}^{\bf +}}} $ anomaly
- Received Date: 2024-08-14
- Available Online: 2025-01-15
Abstract: The Cd puzzle implies that the phonon excitation of a spherical nucleus should be questioned and refuted. To understand the newly and experimentally discovered spherical-like γ-soft mode, the SU3-IBM was recently proposed. In this study, the evolutions of the normal states in






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: