-
In the last few decades, tremendous progress has been made in the experimental synthesis of superheavy elements [1−3]. Two distinct experimental approaches have been employed in the quest to synthesize superheavy nuclei. Hot fusion reactions have been primarily conducted at the FLNR (Dubna, Russia) laboratory, where the elements numbered 113−118 were successfully synthesized by bombarding actinide target nuclei with
$ ^{48} $ Ca [3−27]. Cold fusion reactions have been mainly performed at GSI (Darmstadt, Germany) [2, 3, 8, 19, 22, 28−33] and RIKEN (Tokyo, Japan) [34], where the elements numbered 107−113 were successfully synthesized by bombarding$ ^{208} $ Pb and$ ^{209} $ Bi targets with projectile nuclei such as$ ^{54} $ Cr,$ ^{58} $ Fe,$ ^{64} $ Ni, and$ ^{70} $ Zn. In recent decades, various projectile-target combinations have been attempted in an effort to produce superheavy nuclei with atomic numbers$ Z = 119 $ and$ Z = 120 $ ; however, there has been no evidence to suggest that new elements have been synthesized [35, 36].Currently, the synthesis of superheavy nuclei with atomic numbers greater than 118 faces numerous challenges. For example: (i) For Es and heavier actinides, target nucleus fabrication is extremely challenging. (ii) Reactions conducted with projectiles such as
$ ^{50} $ Ti,$ ^{54} $ Cr,$ ^{58} $ Fe, and$ ^{64} $ Ni bombarding an actinide target have not yet successfully detected the evaporation residue cross section (ERCS) [37]. (iii) In heavy-ion synthesis experiments, finding suitable projectile-target combinations and identifying optimal incident energies are crucial. Furthermore, the cross-section for synthesizing elements with atomic number$ Z $ >118 is extremely low, falling below the detection efficiency limit of existing detectors (0.1 pb). Therefore, not only is it necessary to theoretically determine the optimal projectile-target combinations and incident energies, but also to enhance key technologies such as detection efficiency and beam intensity [38].Many methods for studying the mechanisms of heavy-ion fusion evaporation reactions have been theoretically developed, such as the dinuclear system (DNS) model [3, 22, 24−27, 39−41], fusion by diffusion [42−48], time-dependent Hartree-Fock theory (TDHF) model [49−55], and some other models [56−65]. However, these methods predict cross-sections for the same projectile-target combinations, which can vary by several orders of magnitude, and the peak values of the excitation functions can differ by several MeV. Inspired by significant discrepancies in results from various theoretical approaches, we choose three projectile-target combinations for theoretical calculations,
$ ^{54} $ Cr +$ ^{243} $ Am [66, 67],$ ^{51} $ V +$ ^{248} $ Cm [67−71], and$ ^{50} $ Ti +$ ^{249} $ Bk [67−70, 72−74], and select the optimal projectile-target combination and incident energy for the synthesis of$ Z = 119 $ . -
In the DNS concept, the ERCS is calculated as a summation over all partial waves J [75],
$ \begin{aligned} \sigma_{\mathrm{ER}}\left(E_{\mathrm{c.m}.}\right)=\sum_{J}\sigma_{\mathrm{\rm{cap}}}\left(E_{\mathrm{c}. \mathrm{m}.}, J\right) P_{\mathrm{\rm{CN}}}\left(E_{\mathrm{c}. \mathrm{m}.}, J\right) W_{\text {sur }}\left(E_{\mathrm{c}. \mathrm{m}.}, J\right), \end{aligned} $

(1) where
$ E_{\rm{c.m.}} $ is the incident energy in the center-of-mass frame. The capture cross section$ \sigma_{\rm{cap}} $ is calculated using an empirical coupled-channel approach [76].$ P_{\rm{CN}} $ is the probability that the system evolves from a touching configuration to the compound nucleus in competition with the quasifission. The final term$ W_{\rm{sur}} $ is the survival probability of the formed compound nucleus, which can be estimated via a statistical model.The capture cross section
$ \sigma_{\rm{cap}}(E_{\rm{c.m.}}) $ at a given center-of-mass energy$ E_{\rm{c.m.}} $ can be written as [77]$ \begin{aligned}\sigma_{\rm{cap}}(E_{\rm{c.m.}})=\frac{\pi\hbar^{2}}{2\mu E _{\rm{c.m.}}}\sum_{J}(2J+1)T(E_{\rm{c.m.}},J), \end{aligned}$

(2) where
$ E_{\rm{c.m.}} $ and J represent the incident energy in the center of mass system and angular momentum, respectively.$ T(E_{\rm{c.m.}},J) $ is the penetration probability of the two colliding nuclei overcoming the Coulomb potential barrier in the entrance channel. The capture cross section$ \sigma_{\mathrm{\rm{cap}}}(E_{\mathrm{\rm{c.m.}}}) $ can be estimated using the empirical coupled channel method. We construct different barrier distribution functions based on the different coupling modes between the target and projectile. There are three cases: (i) fusion reactions involving two spherical nuclei, (ii) reactions with two statically deformed nuclei, and (iii) reactions with a combination of one spherical nucleus and one statically deformed nucleus, as addressed in detail in Ref. [76].$ P_{\rm{CN}}(E_{\rm{c.m.}}, J) $ in Eq. (1) is the probability of system evolution from the contact configuration to the formation of the compound nucleus. The time evolution of the probability distribution function$ P(Z_1, N_1, \beta_{12}, \beta_{22}, \theta_{1},\theta_{2}, \varepsilon_1, t ) $ at a fixed directional angle ($ \theta_{1} $ and$ \theta_{2} $ ) can be obtained by solving the master equation for the four variables in the corresponding potential energy surface [78], which is addressed in detail in Ref. [79].Finally, the fusion probability is given by
$ \begin{aligned} P_{\rm{CN}}(E_{\rm{c.m.}},J)=\sum_{Z_{1}=1}^{Z_{\rm{BG}}}\sum_{N_{1}=1}^{N_{\rm{BG}}}\int_{0}^{\infty}\int_{0}^{\infty}\int_{0}^{\pi/2}\sin\theta_{1}{\rm d}\theta_{1}\int_{0}^{\pi/2} \\ P(Z_{1},N_{1},\beta_{12},\beta_{22},\theta_{1},\theta_{2},\tau_{\rm{int}})\rho_{1}(\beta_{12})\rho_{2}(\beta_{22}){\rm d}\beta_{12}{\rm d}\beta_{22}\sin\theta_{2}{\rm d}\theta_{2}. \end{aligned} $

(3) where
$ N_{\rm{BG}} $ and$ Z_{\rm{BG}} $ are the Businaro-Gallone (BG) points. The interaction time$ \tau_{\rm{int}} $ in Eq. (3) determines how far the system travels along the potential energy surface, and the interaction time$ \tau_{\rm{int}} $ in the dissipative process of two colliding nuclei is determined using the deflection function method. Here,$ \rho(\beta_{i})=\dfrac{1}{h_{i}} $ denotes the density of the discrete dots with the step length$ h_{i} $ ($ i = 1,2 $ ), where the step length$ \Delta \beta_{i} $ is 0.05.The survival probability
$ W_{\rm{sur}}(E_{\rm{c.m.}}, J) $ in Eq. (1) for a compound nucleus can be calculated using a statistical method. The survival probability of the excited compound nuclei during deexcitation via the evaporation of neutrons competing with fission is expressed as follows:$ \begin{align} W_{\mathrm{\rm{sur}}}\left(E_{\rm{CN}}^{*}, x, J\right) = F\left(E_{\rm{CN}}^{*}, x, J\right) \prod_{i = 1}^{x}\left[\frac{\Gamma_{n}\left(E_{i}^{*}, J\right)}{\Gamma_{n}\left(E_{i}^{*}, J\right)+\Gamma_{f}\left(E_{i}^{*}, J\right)}\right]_{i}, \end{align} $

(4) where
$ \left(E_{\rm{CN}}^{*}, x, J\right) $ is the realization probability [80] of the xn channel at the excitation energy$ E_{\rm{CN}}^{*}\left(E_{\mathrm{c} . \mathrm{m} .}+Q\right) $ of the compound nucleus with angular momentum J, and i is the index of the evaporation step. The partial widths of neutron emission and fission are$ \Gamma_{n} $ [81, 82] and$ \Gamma_{f} $ [83], respectively.The level density is calculated using the backshift Fermi-gas model,
$\begin{aligned} \rho(U, J) & = \frac{(2 J+1) \exp \left[2 \sqrt{a U}-\frac{J(J+1)}{2 \sigma^{2}}\right]}{24 \sqrt{2} \sigma^{3} a^{1 / 4} U^{5 / 4}}, \end{aligned} $

(5) with
$\sigma^{2}=\dfrac{\Theta_{\text {igid }}}{\hbar^{2}} \sqrt{\dfrac{U}{a}},\; \Theta_{\text {rigid }}=\dfrac{2}{5} m_{u} A R^{2},\; U=E-\delta$ . The back-shifts$ \delta =-\Delta $ (odd-odd), 0(odd-A), and Δ(even-even) are related to the neutron and proton pairing gap$ \Delta=1 / 2\left[\Delta_{n}(Z, N)+\Delta_{p}(Z, N)\right] $ .The dependence of the level-density parameter a on the shell correction and excitation energy was proposed as
$ \begin{aligned} a(U, Z, N) & = \tilde{a}(A)\left[1+E_{\mathrm{sh}} \frac{f(U)}{U}\right] \end{aligned} $

(6) with
$ \tilde{a}(A)=\alpha A+\beta A^{2 / 3} $ and$ f(U)=1-\exp \left(-\gamma_{D} U\right) $ . Note that the differences between the corresponding level-density parameters are primarily due to different shell corrections. Thus, these parameters should be used at the same shell correction energies. The parameters$\alpha = 0.1337$ ,$ \beta =-0.06571 $ , and$ \gamma_{D}=0.04884 $ [84], which are determined by fitting to experimental level-density data with the help of the microscopic shell correction from FRDM1995 [85], are adopted to calculate the level density used in the evaporation calculations.In these calculations, we use the microscopic corrections
$ E_{\rm{shell}} $ given in Ref. [85] as the values of fission barriers for calculating the survival probabilities. In FRDM1995, the microscopic correction$ E_{\rm{mic}} $ ($ E_{\rm{shell}} $ ) is different from the shell plus pairing correction$ E_{s+p} $ . The shell$ E_{s+p} $ ($ E_{\rm{shell}} $ ) contains shell and pairing corrections arising owing to the shell structure of the nuclear system determined solely from the single particle level spectrum at a specific deformation. The microscopic correction is given by$ \begin{aligned} E_{\rm{mic}}(\beta)=E_{s+p}(\beta)+E_{\rm{mac}}(\beta)-E_{\rm{mac}}(0), \end{aligned} $

(7) where
$ E_{\rm{mic}} $ is typically tabulated [85].$ E_{\rm{mic}} $ represents the total gain in the energy of a nucleus due to its shell structure. The difference between$ E_{\rm{mic}} $ and$ E_{s+p} $ is the deformation energy of the macroscopic part of the energy of a nucleus. For superheavy nuclei, the macroscopic energy is flat as a function of deformation, and this difference is small. -
To test the reliability of the DNS model, we calculate the ERCS for
$ ^{48} $ Ca-induced reactions with the target nuclei$ ^{243} $ Am [12, 32, 86],$ ^{248} $ Cm [5, 15, 32, 87], and$ ^{249} $ Bk [20, 32, 88, 89]. The theoretical results are compared with the existing experimental data in Fig. 1. For three projectile-target combinations, considering the uncertainties of the experiments, the theoretical calculations show good agreement with the experimental data, especially for the 3n and 4n evaporation channels.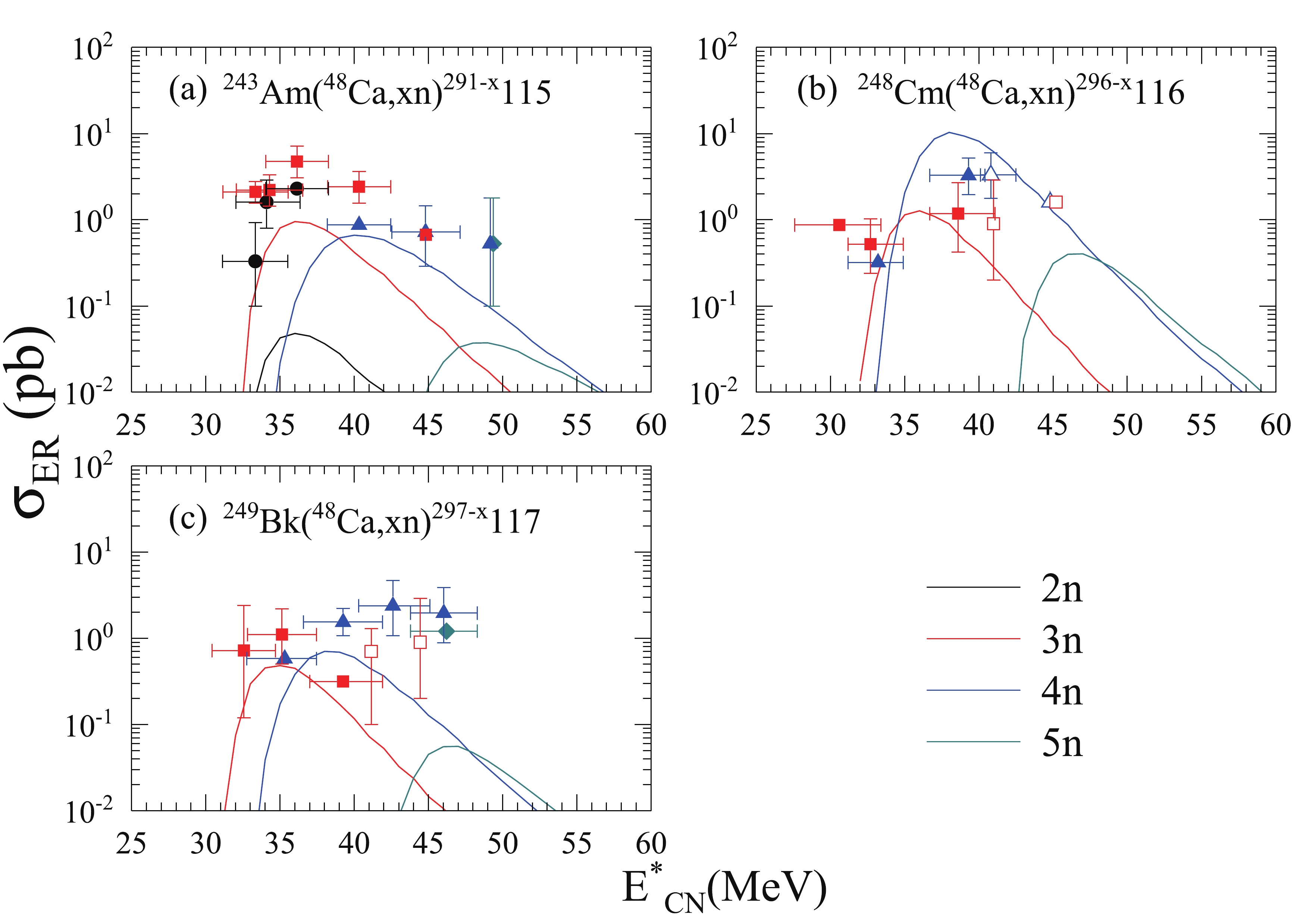
Figure 1. (color online) Calculated ERCRs compared with the available experimental data for the reactions
$ ^{48} $ Ca+$ ^{243} $ Am [12, 32, 86],$ ^{48} $ Ca+$ ^{248} $ Cm [5, 15, 32, 87], and$ ^{48} $ Ca+$ ^{249} $ Bk [20, 32, 88, 89]. The measured ERCRs of the 2n, 3n, 4n, and 5n channels are denoted by black circles, red squares, blue triangles, and dark cyan rhomboids, respectively. The corresponding theoretical values are represented by solid black, solid red, solid blue, and solid dark cyan lines, respectively. The experimental data are taken from DGFRS (solid symbols) and SHIP, BGS, and TASCA (open symbols).We calculate the ERCSs for reactions involving
$ ^{54} $ Cr,$ ^{51} $ V, and$ ^{50} $ Ti with target nuclei ($ ^{243} $ Am,$ ^{248} $ Cm, and$ ^{249} $ Bk) and explore these as potential alternative pathways for the synthesis of new superheavy elements with atomic number$ Z=119 $ . All reactions are calculated using a set of parameters and under the same assumptions.As shown in Fig. 2(a), when transitioning from
$ ^{48} $ Ca to the heavier projectile$ ^{54} $ Cr, the cross sections for the 3n and 4n channels in the$ ^{54} $ Cr +$ ^{243} $ Am reaction decrease by 2−3 orders of magnitude, with the maximum cross-sections for the 2n, 3n, and 4n evaporation channels being 0.067 pb, 0.076 pb, and 0.003 pb at excitation energies of$ E^{*}_{\rm{CN}} $ = 27, 33, and 42 MeV, respectively. The ERCSs are 1−2 orders of magnitude lower than the current experimental technical limit (greater than 0.1 pb [90]). At present, the Institute of Modern Physics, Lanzhou, China is conducting experiments involving$ ^{54} $ Cr bombarding$ ^{243} $ Am.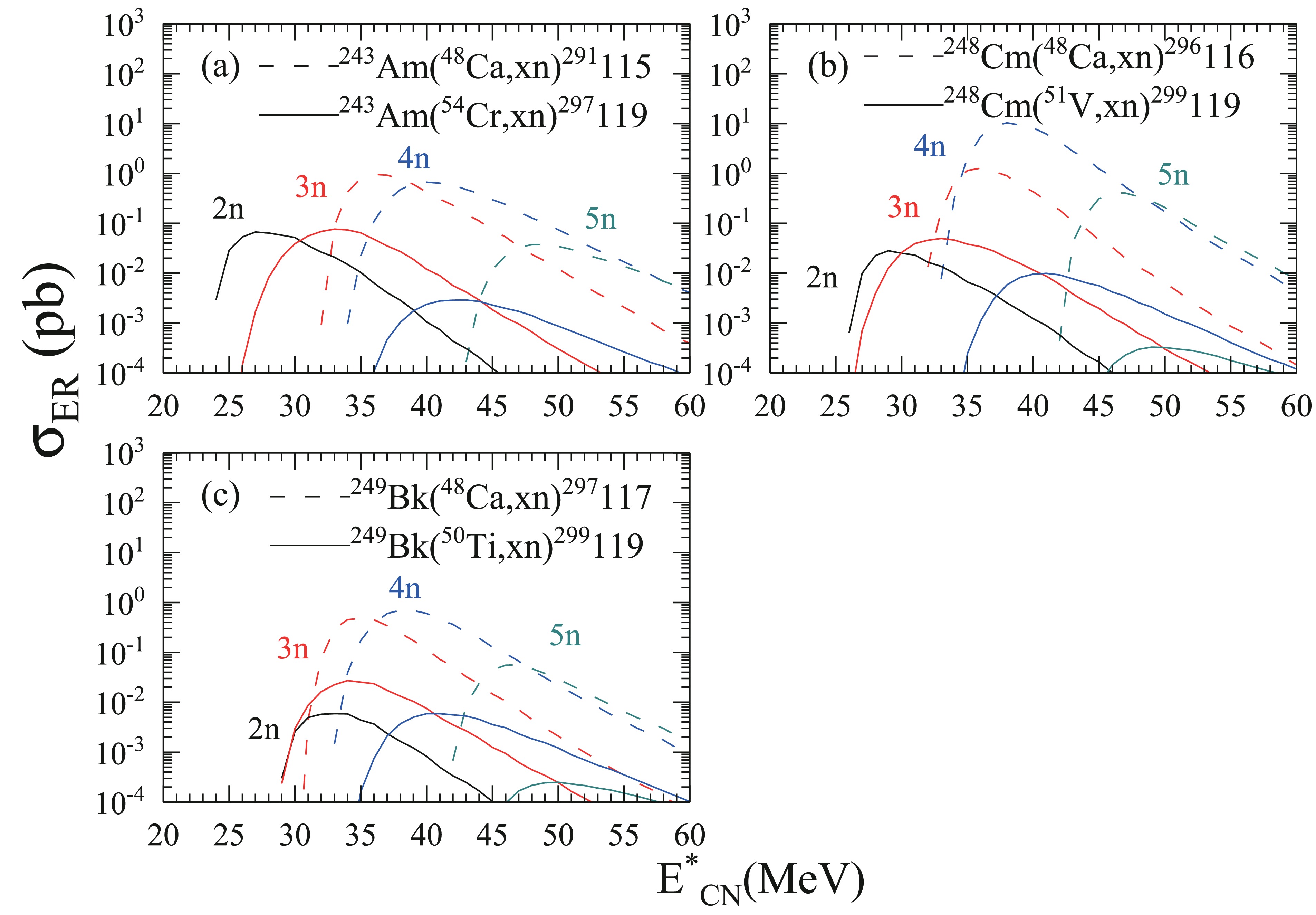
Figure 2. (color online) Evaporation residue cross sections of
$ ^{48} $ Ca+$ ^{243} $ Am,$ ^{48} $ Ca+$ ^{248} $ Cm,$ ^{48} $ Ca+$ ^{249} $ Bk (dashed lines),$ ^{54} $ Cr+$ ^{243} $ Am,$ ^{51} $ V+$ ^{248} $ Cm, and$ ^{50} $ Ti+$ ^{249} $ Bk (solid lines) for the 3n, 4n, and 5n channels are denoted by red, blue, and dark cyan lines, respectively.For the
$ ^{51} $ V +$ ^{248} $ Cm reaction, predictions are made for the ERCSs of the 2n, 3n, and 4n evaporation channels, leading to the production of isotopes$ ^{297} $ 119,$ ^{296} $ 119, and$ ^{295} $ 119. The ERCS excitation functions are depicted in Fig. 2(b). The maximum ERCSs in the 2n, 3n, and 4n evaporation channels are 0.028, 0.050, and 0.010 pb at excitation energies of$ E^{*}_{\rm{CN}} $ = 29, 33, and 41 MeV, respectively. The above ERCSs are one order of magnitude below the present experimental technique limit (greater than 0.1 pb [90]). In 2022, Tanaka et al. [91] successfully obtained the barrier distribution of the$ ^{51} $ V +$ ^{248} $ Cm system during the operation of SRILAC by measuring the quasi-elastic (QE) backscattering cross-sections of GARIS-III. To date, no related events have been observed [92].Figure 2(c) shows the predicted excitation functions for the
$ xn $ ERCSs of the$ ^{50} $ Ti +$ ^{249} $ Bk reaction. The maximum cross sections for the 2n, 3n, and 4n evaporation channels are 0.006 pb 0.017 pb, and 0.006 pb at excitation energies of$ E^{*}_{\rm{CN}} $ =33, 37, and 40 MeV, respectively. As shown in Fig. 2(c), compared to the$ ^{48} $ Ca +$ ^{249} $ Bk reaction, the ERCSs for$ ^{50} $ Ti and heavier actinide targets are significantly smaller. The ERCSs for the$ ^{50} $ Ti +$ ^{249} $ Bk reaction system are approximately two orders of magnitude smaller than the measured results for the$ ^{48} $ Ca +$ ^{249} $ Bk reaction system. The GSI laboratory in Germany once attempted to synthesize a new element with Z=119 using the$ ^{50} $ Ti +$ ^{249} $ Bk reaction. However, the upper limit of the obtained production cross-section for the isotope of element 119 was only 50 fb [93].In 2015, Mayorov et al. [94] conducted an intriguing experiment within the heavy nucleus region. The excitation functions for the
$ xn $ evaporation channels, as measured using the$ ^{50} $ Ti and$ ^{54} $ Cr induced reactions, were compared with the measured results of the$ ^{48} $ Ca induced reactions with$ ^{162} $ Dy. They found that the maximum cross section of the 4n evaporation channel for the$ ^{48} $ Ca +$ ^{162} $ Dy reaction was 74 and 109 times greater than the maximum cross sections for the$ ^{50} $ Ti and$ ^{54} $ Cr reactions with$ ^{162} $ Dy, respectively. In the realm of superheavy elements, it is important to note that the ERCSs derived from theoretical calculations for reactions involving$ ^{54} $ Cr and heavier projectiles with actinide targets are significantly lower than those of the$ ^{48} $ Ca-induced reaction.The ERCS is obtained via the product of the capture cross section, fusion probability, and survival probability. It is primarily determined using the fusion and survival probabilities. Generally, asymmetric systems are more favorable for the synthesis of superheavy nuclei because the fusion probability decreases significantly with an increase in the product of the projectile and target nuclear charge numbers. However, for more symmetric systems, the loss in fusion probability can also be compensated for by an increase in survival probability.
In Table 1, we compare the maximum cross sections predicted in our study with those obtained using various computational methods from the cited literature. The optimal incident energies and maximum ERCSs from different models and parameters vary greatly. The accurate prediction of the optimal incident energies for experiments is one of the biggest challenges to synthesizing new elements beyond
$ Z=118 $ . However, the calculated results for the optimal incident energy show great uncertainty and model dependence. This is mainly because the optimal incident energy is related to the Coulomb barrier height, reaction Q value, and internal fusion barrier height, which are model-dependent. Moreover, a method for exactly defining the internal fusion barrier is yet unknown. To determine the optimal incident energy, the newly developed method is weakly model dependent [95], which is extremely important for the experimental synthesis of superheavy nuclei.Reference Method Mass table $ ^{54} $ Cr+

$ ^{243} $ Am

$ ^{51} $ V+

$ ^{248} $ Cm

$ ^{50} $ Ti+

$ ^{249} $ Bk

$ ^{48} $ Ca+

$ ^{254} $ Es

$ ^{48} $ Ca+

$ ^{252} $ Es

V. Zagrebaev 2008 [72] ECC+P $ _{\rm{CN}} $ +SA

FRDM1995 [85] − 50 fb − − M.-H. Huang 2010 [96] DNS − − − − 0.3 pb(3n) 1.5 pb(4n) Z.-H. Liu 2011 2D coupled LEs FRLDM [98, 99] − 0.57 pb(4n) − − 0.2 pb(4n) Z.-G. Gan 2011 [100] DNS − − − − 1.2 pb(4n) 0.25 pb(3n) N. Wang 2012 [73] DNS-DyPES FRDM1995 [85] − − 0.11 pb(4n) − − K. Siwek-Wilczynska 2012 [97] FBD Kowal 2010 [101] − − − 15 fb(4n) 0.2 pb(4n) L. Zhu 2014 DNS FRDM1994 [102] − 0.055 pb(3n) 0.064 pb(4n) − 0.96 pb(4n) M. Kowal 2016 [37] FBD Kowal 2010 [101] − − − − 0.2 pb(4n) N. Ghahramanya 2016 [68] − AME2012 [103] − 99.6 fb(4n) 0.15 pb(4n) 0.18 pb(4n) − K. Siwek-Wilczynska 2019 [69] FBD Kowal 2010 [101] − 5.9 fb(4n) 35.6 fb(4n) 0.16 pb(4n) 0.2 pb(4n) G. G. Adamian 2019 [70] DNS FRDM1995 [85] − 44 fb 39.4 fb − − G. G. Adamian 2020 [74] HFB + micro-macro model FRDM2012 [104] − − 19 fb − − X.-J. Lv 2021 [67] ECC+P $ _{\rm{CN}} $ +SA

− 1.82 fb(3n) 9.2 fb(4n) 48.2 fb(3n) − − B. M. Kayumov 2022 [66] DNS FRDM1995 [85, 105] 25 fb(3n) − − − − A. Nasirov 2024 [71] DNS FRDM1995 [85] − 12.3 fb(4n) − − − This study DNS FRDM1995 [85] 0.076 pb(3n) 0.05 pb(3n) 0.017 pb(3n) − − For the maximum cross sections, all of the aforementioned theories provide roughly the same product of
$ \sigma_{\rm{cap}}P_{\rm{CN}}W_{\rm{sur}} $ . In Eq. (1), each factor that influences the production cross section of superheavy nuclei through complete fusion reactions has its own uncertainties. Theoretically, the capture cross section in Eq. (2) plays a significant role in the synthesis process of superheavy nuclei. Consequently, extensive research has been conducted on the capture cross section, notably when using projectiles with atomic number Z$ > $ 20 for the synthesis of superheavy nuclei [106], most of which do not lead to the formation of superheavy nuclei. Therefore, a thorough investigation of the capture process is essential for understanding the formation mechanisms of superheavy nuclei.Equation (3) represents the fusion probability
$ P_{\rm{CN}} $ , which has a significant impact on the fusion evaporation cross section and is an important factor in its calculation [41]. Not only is the value of$ P_{\rm{CN}} $ uncertain, but its dependence on the excitation energy and reaction entrance channel is also uncertain. To calculate the fusion probability, the various theoretical methods mentioned above require the potential energy surface estimated via the macro-microscopic model as the input [48, 107]. The calculation of the multidimensional potential energy surface is a complex physical issue that has not been fully resolved because selecting suitable degrees of freedom is an important and difficult task. To numerically analyze the corresponding dynamic equations, the number of degrees of freedom cannot be too large. This means that the calculated potential energy surface is the upper limit of the most favorable potential energy that the nucleus can accept. Therefore, the potential energy surface and$ P_{\rm{CN}} $ of heavy ion fusion reactions are not yet fully understood.Equation (4) represents the survival probability
$ W_{\rm{sur}} $ , which is influenced by factors such as the fission barrier, neutron separation energy, level energy density parameter, and shell damping factor. Our calculated ERCSs are based on nuclear data such as nuclear masses, neutron separation energies, and fission barriers (shell correction energies), which are typically extrapolated. Therefore, our accuracy is closely related to the accuracy of the extrapolation. In particular, in the cross-section calculations for the synthesis of superheavy nuclei, the precision of the fission barrier is crucial. In hot fusion reactions, the compound nucleus releases three to four neutrons. When the height of the fission barrier is imprecise, the calculation errors in the neutron decay width and fission width ratio at each step of the (xn) de-excitation cascade accumulate, leading to a larger error in the calculated cross section. In addition, these two different shell effect damping methods offer distinctly different predictions for the survival probability [108, 109]. -
The DNS model in this study primarily takes the deformation of the interacting nuclei as the independent variable. The evolution of the DNS is regarded as a diffusion process. The process of nucleon transfer and rearrangement within the DNS is described by numerically solving the transport equation (master equation) on the corresponding potential energy surface. We calculate the ERCSs for the reactions
$ ^{48} $ Ca +$ ^{243} $ Am,$ ^{48} $ Ca +$ ^{248} $ Cm, and$ ^{48} $ Ca +$ ^{249} $ Bk and compare them with available experimental data. The results show that the theoretical calculations can effectively reproduce the experimental trends in the 3n and 4n evaporation channels of these reaction systems.For the synthesis of new element with atomic number
$ Z=119 $ , we predict the ERCSs for three reaction systems ($ ^{54} $ Cr +$ ^{248} $ Am,$ ^{51} $ V +$ ^{248} $ Cm, and$ ^{50} $ Ti +$ ^{249} $ Bk) to select the most promising projectile-target combination. In addition, through comparisons with different models, we find significant differences in the optimal incident energies and maximum ERCSs under different model parameters. These discrepancies mainly stem from the use of varying fission barriers and ground-state masses in these calculations. However, we also note that, considering feasible target combinations under current experimental conditions, the maximum cross sections predicted by our model and other methods appear to be below the detection limits of current experimental facilities. Therefore, synthesizing superheavy nuclei with$ Z = 119 $ will require improvements in beam intensity, detection techniques, and effective separation methods.
Possibility of synthesizing Z = 119 superheavy nuclei with Z > 20 projectiles
- Received Date: 2024-08-16
- Available Online: 2024-12-15
Abstract: We employ the dinuclear system (DNS) model combined with a statistical model to calculate the evaporation residue cross sections of the reaction systems





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: