-
The quark-antiquark potential is one of the best studied quantities in QCD owing to its importance in spectroscopy and phenomenology. In the early stages of QCD development, it was related to the large time behavior of Wilson loop expectation values [1, 2]. These values can be computed in lattice QCD. Thus, lattice QCD has been regarded as the main tool for studying the quark-antiquark potential, being the resulting potential consistent with phenomenology [3−18]. Meanwhile,
$ {\rm{AdS/CFT}} $ correspondence [19−21] opened a new window for addressing strongly coupling gauge theories. Within the AdS/CFT correspondence, the expectation values of an operator similar to the Wilson loop can be calculated [22, 23]. Consequently, the study of the quark-antiquark potential using gauge/string duality has received attention. Reference [22] is the earliest study in the literature that analyzed the static quark-antiquark potential using gauge/string duality. It showed that this potential exhibits Coulombian behavior at short distances. The pseudopotential of quark-antiquark pairs was extended in Refs. [24−26], and the influence of chemical potential on the pseudopotential was discussed in [27−30]. These studies found that the quark-antiquark pseudopotential at any temperature and chemical potential exhibits Coulomb-like behavior at short distances and linear behavior at long ranges. After that, some extreme conditions (e.g., rotating meson, rotating matter, anisotropy, and magnetic field) [29, 31−36] and holographic models of multiquark (pseudo)potential [30, 37−48] were studied.Moreover, QCD predicts the existence of hybrid mesons and baryons in which the gluonic field between a quark and antiquark is in an excited state. Thus, hybrids containing the excited gluonic field are an important source of information related to QCD. The properties of hybrid mesons and baryons were predicted by lattice simulations reported in Refs. [49, 50]. The hybrid static potentials have been the focus of extensive calculations in lattice QCD [5, 10, 14, 15, 50−58]. To the best of our knowledge, there are currently no studies on the pseudopotential of hybrid mesons and baryons in lattice QCD simulations.
Prior to discussing the hybrid pseudopotentials, let us briefly consider the quark-antiquark pseudopotential. This pseudopotential, which is confining at all temperatures, can be extracted from the expectation value of a Wilson loop [59, 60]. This is achieved by adopting an important example, namely a rectangular Wilson loop of size
$ L \times Y $ , oriented in the$ x y $ -plane. In this case, the expectation value of the Wilson loop is [61]$ \langle W (L \times Y)\rangle \sim \sum\limits_{n=0}^{\infty} c_n (L) {\rm e}^{-E_n(L) Y}. $

(1) If the corresponding contribution dominates the sum as
$ Y \rightarrow \infty $ , E represents the pseudopotential, and the other values of$ E_n $ are called hybrid pseudopotentials.Inspired by the AdS/CFT correspondence, Andreev et al. proposed a model within a five(ten)-dimensional effective string theory. Originally, this model was used to compute the quark-antiquark (pseudo)potential [26, 62] and the three-quark (pseudo)potential [37] and exotic states [63]. By inserting a new object called "defect'' on a string linking quark and antiquark, the model was further developed to calculate the exotic hybrid potential [64] and pseudopotential [61] of quark-antiquark pairs. For example, consider
$ \Sigma_u^- $ , which represents the first excited state of the Σ meson, and$ \Sigma_g^+ $ , which represents the ground state of the Σ meson; the resulting hybrid potential at zero temperature reported in Ref. [64] perfectly matches the lattice simulations reported in Ref. [65]. In Ref. [64], it was pointed out that the$ \Sigma_u^- $ hybrid pseudopotential no longer exhibits Coulomb-like behavior at short distances.The Large Hadron Collider and relativistic heavy-ion collision experiments simulate high-temperature and high-density environments in the laboratory. Research on exotic hybrid pseudopotentials at finite temperature and chemical potential provides the theoretical background for these experiments, guiding the observation and interpretation of results. Neutron stars and other dense astrophysical objects may exhibit extreme temperature and chemical potential conditions internally. Studying pseudopotentials under these conditions can provide insights into the state of matter and its interactions within these celestial bodies.
In this study, we extended hybrid pseudopotentials to finite temperature and chemical potential. That is to say, we aimed to elucidate how the temperature and chemical potential affect hybrid pseudopotentials. The paper is organized as follows. In Sec. II, a string configuration of exotic hybrid mesons is briefly introduced. In Sec. III, we describe a specific application example of the ten-dimensional effective string theory at finite temperature and chemical potential. This theory, which was proposed by Andreev, effectively describes the static potential of
$ \Sigma_g^+ $ and$ \Sigma_u^- $ at zero temperature and chemical potential [61, 64]. We extended it to finite chemical potential and calculated the hybrid pseudopotential of$ \Sigma_u^- $ at finite temperature and chemical potential. In Sec. IV, we present the numerical results and compare the$ \Sigma_u^- $ hybrid pseudopotential with the$ \Sigma_g^+ $ pseudopotential. The last section contains discussion and conclusions. -
In this section, we first briefly review a string configuration of exotic hybrid mesons. It is commonly suggested that the ground state energy of a U-shape string linking two fermionic sources corresponds to the potential of a quark-antiquark pair and that the excited strings (fluxes) induce hybrid potentials [49]. The string excitations can be modeled by inserting local objects on the linking string. If we take into account that some excitations remain very narrow along a string. these objects, called defects, are simply the macroscopic description of a gluonic degree of freedom in strong coupling [61, 64]. It should be noted that when defects are inserted, the string embeddings of the world sheets in spacetime become non-differentiable at the locations of these defects. This model, considering the case of a single defect, was used in Ref. [64] to perfectly reproduce the lattice data of Ref. [65] for the
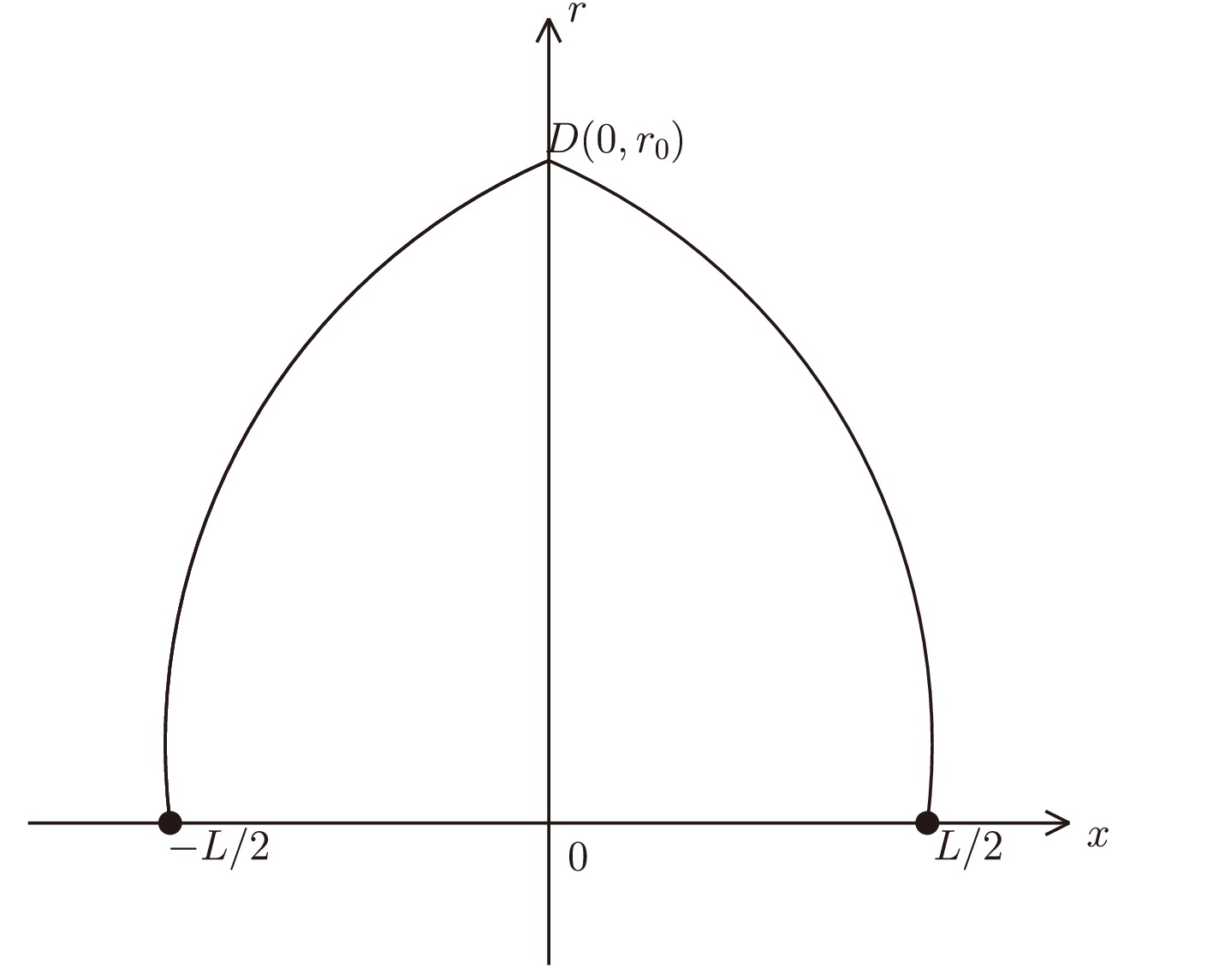
$ \Sigma_u^- $ hybrid potential at zero temperature and in Ref. [61] to predict the$ \Sigma_u^- $ hybrid pseudopotential at finite temperature. In this study, we extended the model to finite temperature and chemical potential and examined the influence of temperature and chemical potential on exotic hybrid pseudopotentials corresponding to the excited state.Fig. 1 shows a possible configuration of a hybrid quark-antiquark pair. In this string configuration, the quark (or anti-quark) located at the boundary points of a five (ten) dimensional space is the endpoint of a fundamental string. These two fundamental strings connect at an internal defect. It should be noted that we set two symmetries to simplify the string configuration based on the accurate analysis reported by Andreev in Refs. [61, 64]. Thus, this string configuration sits entirely on the
$ xor $ plane ($ {y_D}=0 $ ), and the defect D must be on the r-axis ($ {x_D}=0 $ ).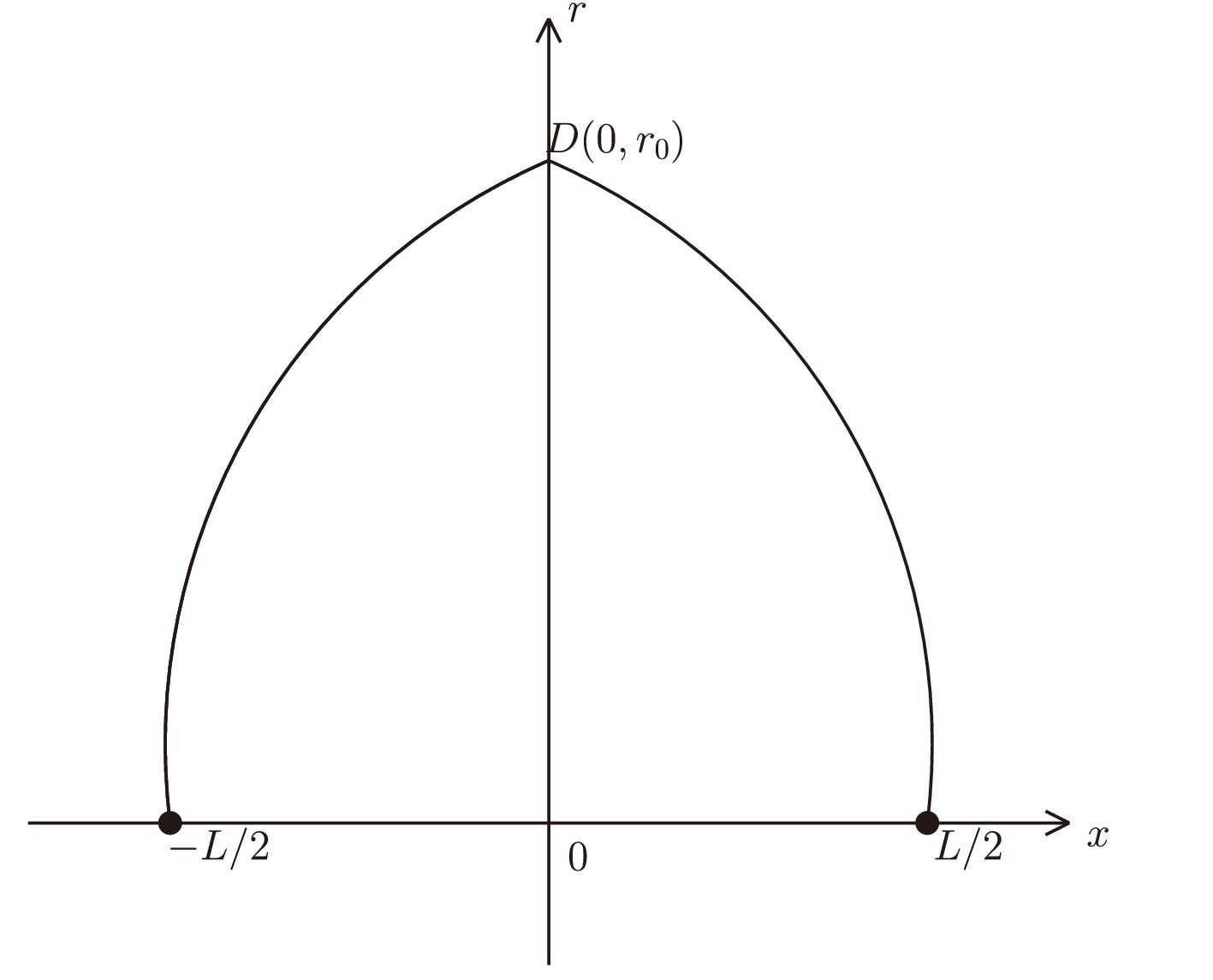
Figure 1. A string configuration of the hybrid quark-antiquark pair in the case of a single symmetrical defect. The quark and antiquark are on the x-axis at
$ x=L/2 $ and$ x=-L/2 $ , respectively. The defect D is located on the$ xor $ plane. If there is no defect D, the string configuration can be described as the quark-antiquark pair corresponding to a ground state connected by a U-shape string.In such a string configuration with a single symmetrical defect (Fig. 1), the action not only includes two standard Nambu-Goto actions but also the contribution arising from the defect. Therefore, we have that
$ S=\sum\limits_{i=1}^2 S^{{\rm{(N G)}}}_i +S^{{\rm{(def)}}} , $

(2) where
$ S^{{\rm{(N G)}}}_i $ denotes the Nambu-Goto action of the string linking the i fermionic source (quark or antiquark) and the defect D.$ S_{{\rm{def}}} $ is considered the action for the defect, which can be expressed as [61, 64]$ S^{{\rm{(def)}}}(r_0) = {T}\; \cdot \; {\cal{E}}^{{\rm{(def)}}}(r_0), $

(3) where
$ {\cal{E}}^{{\rm{(def)}}}(r_0) $ is assumed to be the effective potential for the defect D. Note that its specific form requires the framework of the AdS/QCD duality. -
We used the
$ \Sigma_u^- $ hybrid meson as a specific example to compute the hybrid pseudopotentials of a quark-antiquark pair based on the string configuration described in the previous section. As reported in Refs. [61, 64], the single defect lives in a ten-dimensional space. In such a space, there is nothing but a brane-antibrane pair [66]. At the leading order in$ \alpha' $ , the brane action is assumed to be$S^{{\rm{(def)}}} \sim \tau_5 \int {\rm d}^6 x \sqrt{g^{(6)}}$ because the branes discussed in this model are fivebranes [66]. Here,$ \tau_5 $ is a brane tension and$ x^{i} $ denotes the world-volume coordinates. Then, the ten-dimensional geometry at finite temperature and chemical potential for subsequent application is expressed as [38, 67, 68]$ \begin{aligned}[b] {\rm d} s^{2}={\cal{R}}^{2}\varpi(r)\left(f(r){\rm d} t^{2}+{\rm d} \vec{x}^{2}+ f^{-1}(r) {\rm d} r^{2}\right)+\mathrm{e}^{-\mathfrak{s} r^{2}} g_{a b}^{(5)} {\rm d} \omega^{a} {\rm d} \omega^{b}, \\ \varpi(r)=\dfrac{{\rm e}^{\mathfrak{s} r^{2}}}{r^{2}},\;\;\;\;f(r)=1-(1 + Q^2) \left(\dfrac{r}{r_h}\right)^{4}+ Q^{2} \left(\dfrac{r}{r_h}\right)^{6}. \end{aligned} $

(4) This is a one-parameter deformation of an Euclidean
$ AdS_5 $ space with constant radius$ {\cal{R}} $ and a five-dimensional compact space (sphere)$ {X} $ whose coordinates are$ \omega^a $ . Here,$ \mathfrak{s} $ is a one-parameter deformation that can be fixed from the quark-antiquark potential corresponding to the ground state at vanishing temperature and chemical potential, and Q is the black-hole charge. The parameter$ r_h $ , which represents the position of the black-hole horizon, is related to the Hawking temperature of the black hole. This can be identified with the temperature of a dual gauge theory defined as$ T=\frac{1}{4 \pi}\left|\frac{{\rm d} f}{{\rm d} r}\right|_{r=r_{h}}=\frac{1}{\pi r_{h}}\left(1-\frac{1}{2} Q^{2}\right), $

(5) where Q is in the range of
$ 0 \leq Q \leq \sqrt{2} $ to ensure positive temperature. In this study, the relationship between the chemical potential μ and Q is$ \mu={Q}/{r_{h}} $ . Note that the chemical potential is not the real quark (or baryon) chemical potential in QCD but corresponds to the R-charge of the$ N = 4\; {\rm{SYM}} $ theory.For subsequent computations, we assumed that the fivebranes wrap on
$ \mathbf{R} \times {X} $ , where$ \mathbf{R} $ is represented along the y-axis in the deformed$ {AdS}_{5} $ . The action$ S^{{\rm{(def)}}} $ contributed by an extra item arising from the defect D in Eq. (3) is expressed as$ S^{{\rm{(def)}}} = \mathfrak{m} {\cal{R}} \int {\rm d} t \frac{\mathrm{e}^{- 2 \mathfrak{s} r^{2}}}{r} \sqrt{f(r)}, $

(6) with
$\mathfrak{m} \sim \tau_5 \int {\rm d}^5 \omega \sqrt{g^{(6)}}$ . The extra term of the effective pseudopotential comes from the contribution of the defect D and can be expressed as$ {\cal{E}}^{{\rm{(def)}}}(r_0) = \frac{S^{{\rm{(def)}}}(r_0)}{T} = \mathfrak{m} {\cal{R}} \frac{\mathrm{e}^{- 2 \mathfrak{s} r_0^{2}}}{r_0} \sqrt{f(r_0)}. $

(7) Let us now return to the calculation of the standard Nambu-Goto action
$ S^{{\rm{(N G)}}}_i $ of the string linking the i- fermionic source and the defect D. If we choose the static gauge defined by$ \xi^{1}=t $ and$ \xi^{2}=r $ , then the boundary conditions for$ x(r) $ become$ x^{(1)}(0)=-\frac{L}{2}, \;\;\;\; x^{(2)}(0)=\frac{L}{2}, \;\;\;\; x^{(i)}(r)=0 $

(8) and using the static gauge described by
$ t=\tau, \sigma=x $ , the Nambu-Goto action$ S^{{\rm{(N G)}}}_i $ of one of the two i-strings linking the two fermionic sources (quark or antiquark) and the defect D is$ S^{{\rm{(N G)}}}_i=\frac{1}{2 \pi \alpha^{\prime}} \int {\rm d} \tau {\rm d} \sigma \sqrt{\operatorname{det} g_{\alpha \beta}}, $

(9) with
$ g_{\alpha \beta}=G_{\mu \nu} \frac{\partial x^{\mu}}{\partial \sigma^{\alpha}} \frac{\partial x^{\nu}}{\partial \sigma^{\beta}}, $

(10) where
$ x^{\mu} $ and$ G_{\mu \nu} $ are the target space coordinates and the metric, respectively, and$ \sigma^{\alpha} $ , along with$ \alpha = 0, 1 $ , parameterize the world sheet.The Nambu-Goto action of the left string in Fig. 1 (which we refer to as
$ S^{{\rm{(N G)}}}_1 $ ) can be expressed as$ S^{{\rm{(N G)}}}_{1}=\mathfrak{g}\,{T} \int_{-\frac{L}{2}}^{0} {\rm d} x \varpi(r) \sqrt{f(r)+\left(\partial_{x} r\right)^{2}}, $

(11) where
$ \mathfrak{g}=\dfrac{R^2}{2 \pi \alpha^{\prime}} $ is defined for convenience. Given that this string configuration is symmetrical [61, 64], we can easily obtain the relationship$ S^{{\rm{(N G)}}}_2 = S^{{\rm{(N G)}}}_1 $ ($ S^{{\rm{(N G)}}}_2 $ denotes the Nambu-Goto action of the right string represented inFig. 1).Now, the Lagrangian density
$ {\cal{L}}_1 $ of the left string is identified as$ {\cal{L}}_1=\varpi(r) \sqrt{f(r)+\left(\partial_{x} r\right)^{2}}. $

(12) Therefore, we obtain the first integral of the Euler-Lagrange equations,
$ {\cal{H}}_1(r)= {\cal{L}}_1 - \frac{\partial {\cal{L}}_1 }{\partial (\partial_x r )} = \frac{\varpi(r) f(r)}{\sqrt{f(r)+\left(\partial_{x} r\right)^{2}}}, $

(13) which is constant.
At the endpoint
$ r_0 $ where the defect D is located, we have that$ \left.\partial_{x} r\right|_{r=r_{0}}=\tan \alpha $ , and the first integral of the left string at$ r_0 $ can be expressed as$ {\cal{H}}_1(r_0)=\frac{\varpi(r_0) f(r_0) }{\sqrt{f(r_0)+\tan^{2} \alpha}}. $

(14) Then,
$ \partial_{r} x $ can be solved as$ \partial_{r} x = \sqrt{\frac{\varpi(r_0)^2 f\left(r_{0}\right)^{2}}{\left(f\left(r_{0}\right)+\tan ^{2} \alpha\right) \varpi(r)^2 f(r)^{2}-f(r) \varpi(r_0)^2 f(r_0)^{2}}}. $

(15) It should be noted that the left string at the endpoint
$ r_0 $ is not continuous owing to the presence of the defect D, that is,$ \tan \alpha \neq 0 $ with$ \alpha >0 $ . This is also the case for the right string owing to the symmetry of the string configuration.Based on the above results, the separate lengths of the quark and antiquark can be expressed as
$\begin{aligned}[b] L=\;&2 \int_{0}^{r_{0}} \partial_{r} x {\rm d} r = 2 \int_{0}^{r_0} \,{\rm d} r\,\\&\times\sqrt{\frac{\varpi(r_0)^2 f(r_0)^2}{(f(r_0)+\tan ^2 \alpha) \varpi(r)^2 f(r)^2-f(r) \varpi(r_0)^2 f(r_0)^2}}. \end{aligned}$

(16) Regarding
$ E=\dfrac{S}{T} $ , the potential contributed by the strings is$ E^{{\rm{(N G)}}} = 2\mathfrak{g}\int_{0}^{r_{0}} {\rm d} r \varpi(r) \sqrt{1+f(r)(\partial_{r} x)^{2}}. $

(17) Subtracting the divergent term
$\mathfrak{g} \int_0^{\infty} {\rm d}r \frac{1}{r^2}$ , we obtain the potential$ E^{{\rm{(N G)}}} $ contributed by the two fundamental strings,$ E^{{\rm{(N G)}}} = \mathfrak{g}\left[\int_{0}^{r_{0}} {\rm d} r \left(\varpi(r) \sqrt{1+f(r)(\partial_{r} x)^{2}}-\frac{1}{r^2}\right)-\frac{1}{r_0}\right]+C, $

(18) where C is a normalization constant. Note that Eqs. (16) and (18) can be reduced to the separate length and potential of quark-antiquark pairs in the ground state when
$ \left.\partial_{x} r\right|_{r=r_{0}}=\tan \alpha = 0 $ [68]. These equations were used to calculate relevant results of a quark-antiquark pair in the ground state for comparison with those in the excited state.Given the string configuration for an exotic hybrid quark-antiquark pair, the regularized pseudopotentials at finite temperature and chemical potential should be contributed by the two i-strings and the defect D. Therefore, the exotic hybrid pseudopotential corresponding to the hybrid quark-antiquark pair can be expressed as
$ \begin{aligned}[b] E =\;& {\cal{E}}^{{\rm{(def)}}}(r_0) + E^{{\rm{(N G)}}} \\=\;& 2\mathfrak{g}\Bigg[\int_{0}^{r_{0}} {\rm d} r \left(\varpi(r) \sqrt{1+f(r)(\partial_{r} x)^2}-\frac{1}{r^2}\right)\\&-\frac{1}{r_0} + \mathbf{\kappa} \frac{\mathrm{e}^{- {2} \mathfrak{s} r_0^{2}}}{r_0} \sqrt{f(r_0)}\Bigg]+C, \end{aligned}$

(19) where
$ \mathbf{\kappa} = \dfrac{\mathfrak{m} {\cal{R}}}{2\;\mathfrak{g}} $ is a dimensionless parameter.Given that there is no net force acting on the defect D in equilibrium [38, 41, 45, 47], the equation of force balance at the string endpoint
$ r_0 $ leads to$ \varpi(r_{0}) \frac{\tan\alpha}{\sqrt{f(r_0)+ \tan^{2}\alpha}}+\left( \kappa \frac{{\rm e}^{ - {2} \mathfrak{s} r_0^2}}{r_0} \sqrt{f(r_0)}\right)^{\prime}=0. $

(20) Thus, we can easily obtain the expression
$ \tan^{2} \alpha = - f(r_0)+\left[\frac{1}{f(r_0)} -\kappa^2 \mathrm{e}^{- 6 \mathfrak{s} r_0^{2}}\left(1 +4 \mathfrak{s} r_0^{2} - \frac{r_0 f^{\prime}(r_0)}{2 f(r_0)}\right)^2\right]^{-1}. $

(21) Note that this equation can be simplified to
$ \tan^{2} \alpha =0 $ if κ is set to zero. It means that the two fundamental strings are continuous and differentiable at the endpoints$ r_0 $ . Meanwhile, the exotic hybrid pseudopotential described by Eq. (19) is reduced to the result of the ground state. Additionally, if we deactivate the effects of the chemical potential and temperature by setting$ Q = 0 $ and$ T = 0 $ , the results reported in Ref. [64] are reproduced. In Fig. 2, we repeat the energy levels$ \Sigma_g^+ $ and$ \Sigma_u^- $ without temperature and chemical potential reported in Ref. [64], which fit the lattice data in Ref. [65]. The curve corresponding to the$ \Sigma_g^+ $ ground state was calculated using Eqs. (16) and (18). Thus, we obtained$ \mathfrak{g}= 0.176 $ ,$ \mathfrak{s}= 0.44\, {\rm{GeV^2}} $ , and$ C = 0.71\, {\rm{GeV }} $ . The remaining free parameter$ \mathbf{\kappa}= 2000 $ can be determined by fitting the curve of the$ \Sigma_u^- $ potential calculated from Eqs. (16) and (19) when$ \kappa \neq 0 $ . It indicates that the potential of the$ \Sigma_g^+ $ ground state and$ \Sigma_u^- $ excited state at vanishing temperature and chemical potential can be well described by the string configuration shown in Fig. 2.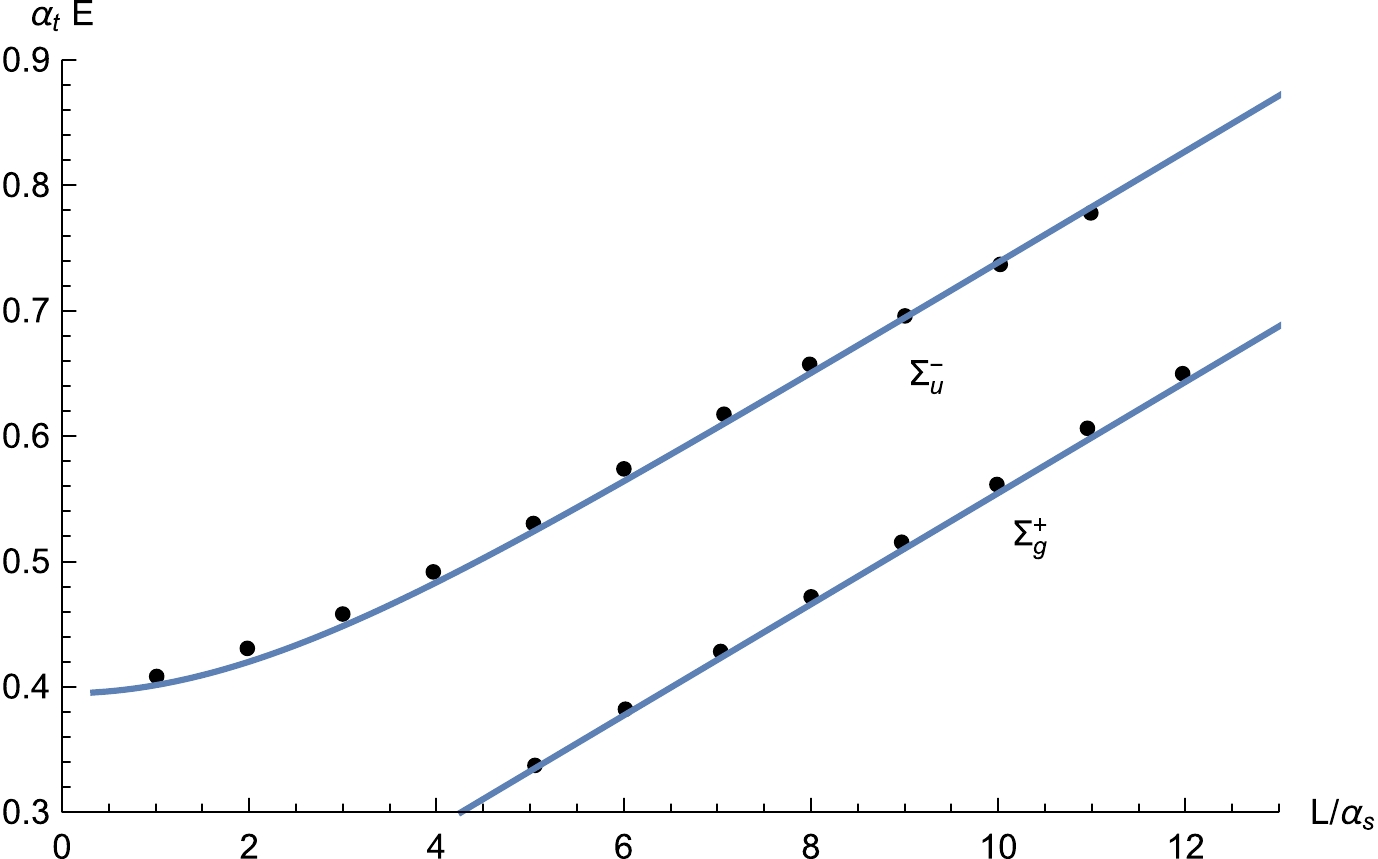
Figure 2. (color online) Energy levels
$ \Sigma_g^+ $ and$ \Sigma_u^- $ without temperature and chemical potential. These curves are our calculation potentials corresponding to the$ \Sigma_g^+ $ ground state and$ \Sigma_u^- $ excited state, respectively, which reproduce the results reported in Ref. [64]. The dots represent the lattice data from Ref. [65]. Here,$ \alpha_s = 0.2 \, {\rm{{fm}}} $ and$\alpha_t \approx 0.41 \, {\rm{{fm}}}.$ At this point of the discussion, we have provided an analytical formula for the pseudopotentials of an exotic hybrid quark-antiquark pair at finite temperature and chemical potential based on the string configuration described in the previous section. In the next section, we use the
$ \Sigma_u^- $ hybrid meson as an example to discuss the effects of temperature and chemical potential on the exotic hybrid pseudopotentials of the quark-antiquark pair. -
In this section, we present numerical results based on the analytical calculations reported in the previous section. We also discuss the effects of temperature and chemical potential on the separate distance and pseudopotentials of an exotic hybrid quark-antiquark pair, respectively. To further analyze the exotic hybrid pseudopotentials, we compare the examples of
$ \Sigma_u^- $ and$ \Sigma_g^+ $ .First, we deactivate the chemical potential effect and only consider the contribution of temperature. Fig. 3 shows the calculations of the separate distance L for
$ \Sigma_g^+ $ and$ \Sigma_u^- $ as a function of$ r_0 $ at different values of temperature T. Note that the quark-antiquark pair in both cases melts as the temperature rises. The red curves represent the melted form, and their maximum values indicate the screening distance of the quark-antiquark pair. Compared to$ \Sigma_g^+ $ (approximately$ 0.132 \; {\rm{GeV}} $ ), the melted temperature of$ \Sigma_u^- $ drops to approximately$ 0.11\; {\rm{GeV}} $ . It means that$ \Sigma_u^- $ (which is the first Σ excited state), as a hybrid meson, is more easily melted than$ \Sigma_g^+ $ , which represents the string ground state. The regularized pseudopotential of$ \Sigma_g^+ $ and$ \Sigma_u^- $ as a function of the separate distance L at different values of temperature is shown in Fig. 4. At short distances ($ L < 0.6 \; {\rm{fm}} $ ), the pseudopotential of$ \Sigma_g^+ $ at any temperature exhibits Coulomb-like behavior, whereas the$ \Sigma_u^- $ hybrid pseudopotential at any temperature behaves as the quadratic term function of the separate distance L. At large distances, both$ \Sigma_g^+ $ and$ \Sigma_u^- $ hybrid pseudopotentials exhibit a linear behavior. In addition, we found that temperature has a minor influence on the$ \Sigma_g^+ $ pseudopotential, with almost no effect at small L. However, the temperature effect on the$ \Sigma_u^- $ hybrid pseudopotential is significant, regardless of whether the separate distance L is large or small.
Figure 3. (color online) Separate distance L corresponding to
$ \Sigma_g^+ $ and$ \Sigma_u^- $ as a function of$ r_0 $ for different values of T without chemical potential: (a)$ \Sigma_g^+ $ ground state at$ \mathfrak{g}= 0.176 $ ,$\mathfrak{s}= 0.44~ {\rm{GeV^2}}$ , and$C = 0.71~ {\rm{GeV }}$ ; (b)$ \Sigma_u^- $ excited state at$ \kappa = 2000 $ .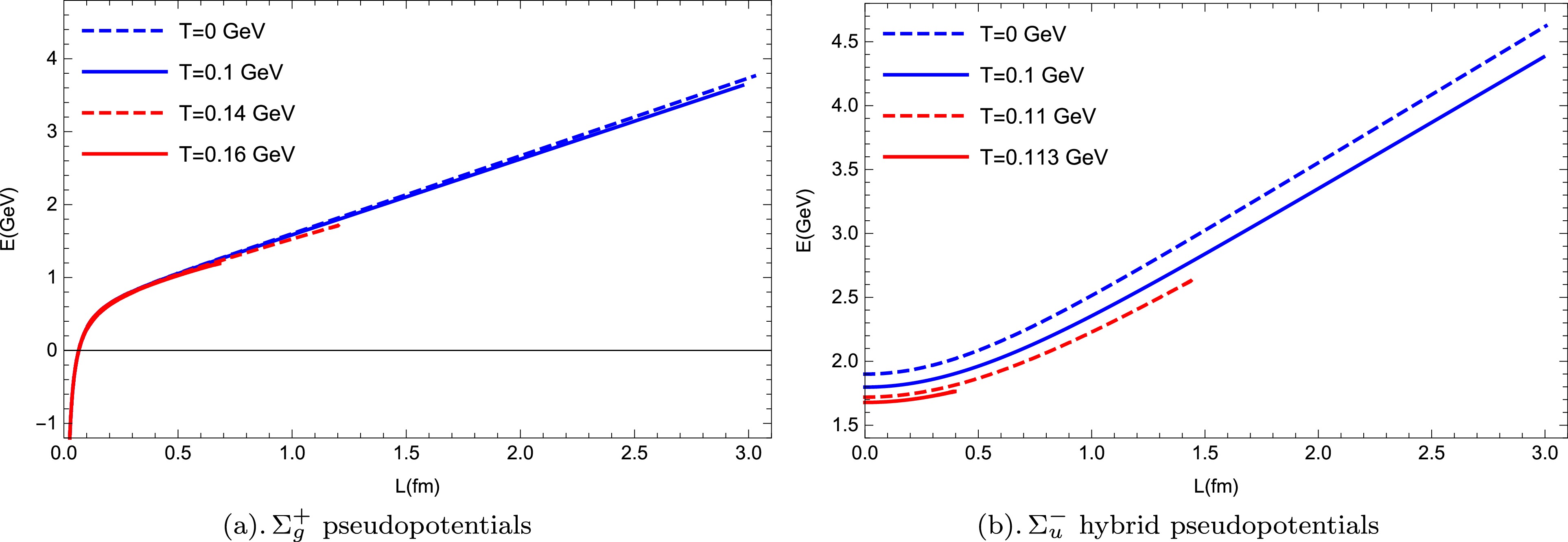
Figure 4. (color online) Regularized pseudopotentials of quark-antiquark pair corresponding to
$ \Sigma_g^+ $ ground state and$ \Sigma_u^- $ excited state as a function of the separate distance L for different values of temperature T at vanishing chemical potential.We also investigated the behavior of the separate distance and pseudopotential at finite temperature and chemical potential; the results are shown in Figs. 5 and 6. The lower temperature was fixed at
$ T = 0.1\, {\rm{GeV}} $ . The separate distance represented as a function of$ r_0 $ for different values of chemical potential μ is shown in Fig. 5. The behaviors of the separate distance of$ \Sigma_u^- $ are qualitatively similar to those of$ \Sigma_g^+ $ . With the increase of chemical potential, the quark-antiquark pair melts. However, the chemical potential required for melting the$ \Sigma_u^- $ excited state is much lower. Fig. 6 shows the calculations of the regularized pseudopotentials for both the ground and excited states at different values of chemical potential μ. At small L, the$ \Sigma_g^+ $ pseudopotentials for any chemical potential are in the Coulomb-like form, while the$ \Sigma_u^- $ hybrid pseudopotentials are in a quadratic function form of L. At long ranges, they both exhibit linear behavior. Reviewing Fig. 4, we discover that the$ \Sigma_u^- $ hybrid pseudopotentials at any temperature and chemical potential are in a quadratic function form at small L and a linear form at large L. Compared with the impact of chemical potential on the$ \Sigma_g^+ $ pseudopotential, which is minimal at large distances and almost negligible at short distances, the chemical potential has a greater impact on the$ \Sigma_u^- $ hybrid pseudopotential. An increase in chemical potential reduces the$ \Sigma_u^- $ hybrid pseudopotential.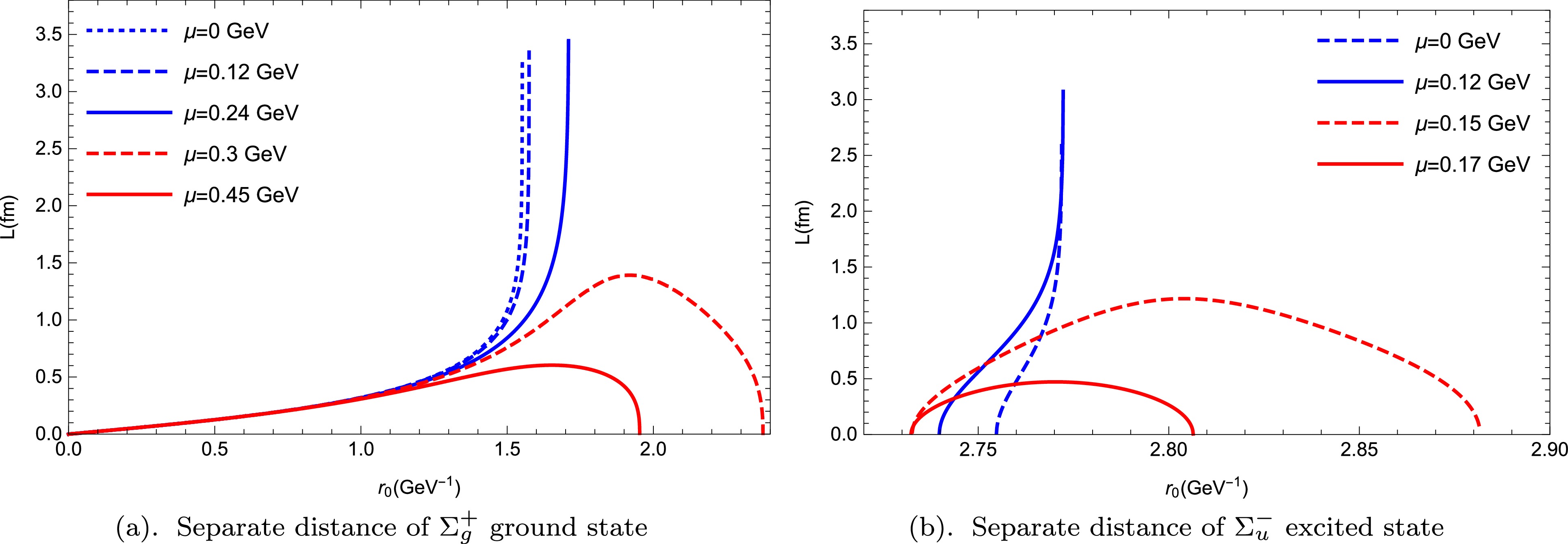
Figure 5. (color online) Separate distance L as a function of
$ r_0 $ for different values of chemical potential at a fixed temperature of$ T = 0.1\, {\rm{GeV}} $ .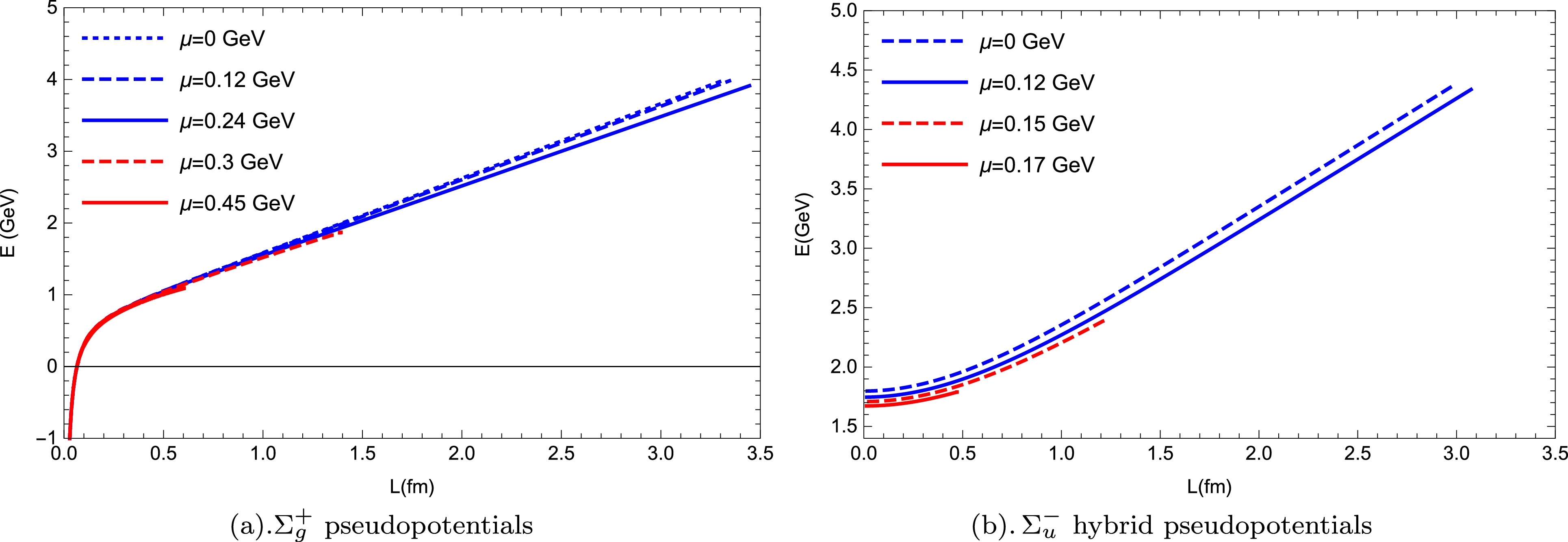
Figure 6. (color online) Regularized pseudopotentials of
$ \Sigma_g^+ $ and$ \Sigma_u^- $ as a function of separate distance L at a fixed temperature of$ T = 0.1 \,{\rm{GeV}} $ for different values of chemical potential μ.To further investigate the influence of chemical potential on the hybrid pseudopotentials, we analyzed the behavior of regularized pseudopotentials at a higher temperature, where a quark-antiquark pair with any chemical potential could be melted. The results of this analysis are shown in Fig. 7. Note that we retained the knee points of the curves, which exactly represent the critical melting points; the abscissa represents the screen distance of the quark-antiquark pair. Fig. 7(a) shows the pseudopotentials of
$ \Sigma_g^+ $ at a higher temperature$ T = 0.15\; {\rm{GeV}} $ and different values of chemical potential:$ \mu= 0.1\; {\rm{GeV}} $ ,$ 0.2\; {\rm{GeV}} $ , and$ 0.3\; {\rm{GeV}} $ . When the chemical potential increases, the screen distance decreases but the$ \Sigma_g^+ $ pseudopotentials barely change. At such a high temperature, the$ \Sigma_g^+ $ pseudopotentials at any value of μ exhibit Coulomb-like behavior before the quark-antiquark pair melts. Meanwhile, Fig. 7 (b) shows the$ \Sigma_u^- $ hybrid pseudopotential curves at a temperature of$ T = 0.11 \,{\rm{GeV}} $ . Note that the$ \Sigma_u^- $ hybrid pseudopotentials for any chemical potential seem to be quadratic functions of the separate distance before melting. The screen distance and hybrid pseudopotentials of$ \Sigma_u^- $ significantly decrease as the chemical potential increases.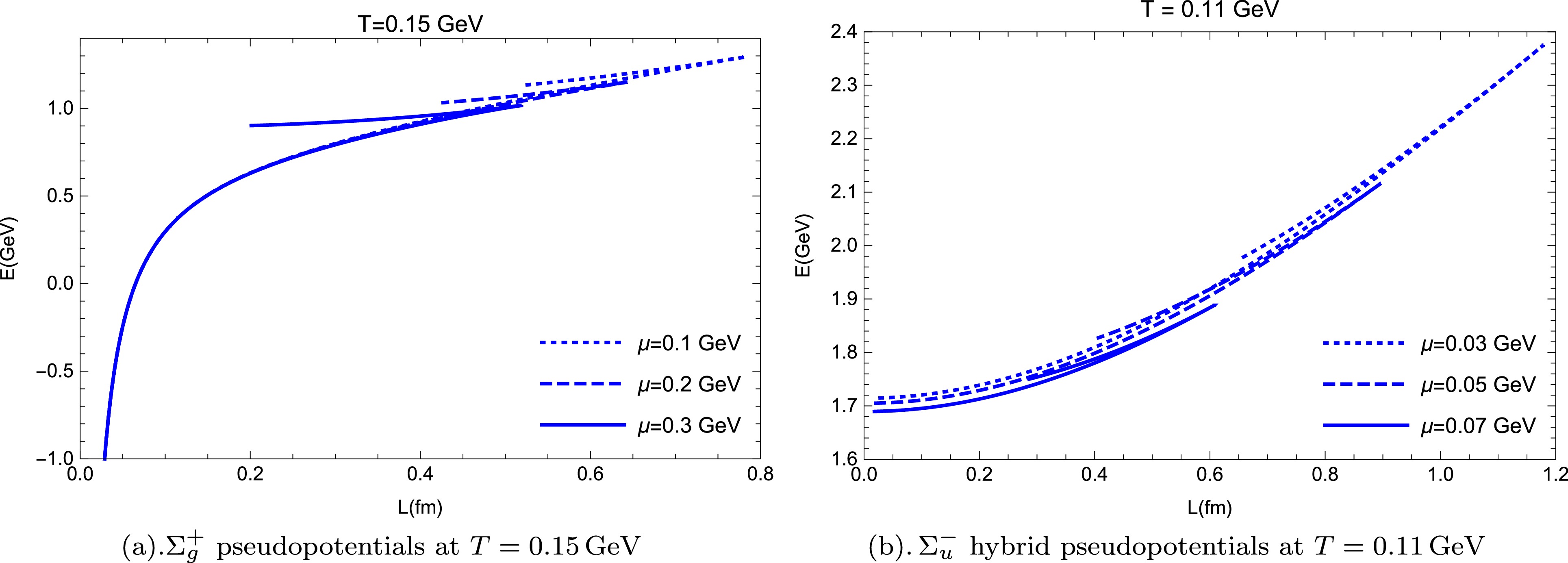
Figure 7. (color online) Regularized pseudopotentials corresponding to
$ \Sigma_g^+ $ and$ \Sigma_u^- $ at higher temperature. The knee points of the curves, which represent the critical melting points, are retained. The lower parts of these curves represent the pseudopotentials: (a)$ \Sigma_g^+ $ pseudopotentials at temperature$ T = 0.15\, {\rm{GeV}} $ and different chemical potentials:$ \mu= 0.1 \,{\rm{GeV}} $ ,$ 0.2 \,{\rm{GeV}} $ , and$ 0.3 \,{\rm{GeV}} $ ; (b)$ \Sigma_u^- $ hybrid pseudopotentials at$ T = 0.11\, {\rm{GeV}} $ and$ \mu= 0.03 \,{\rm{GeV}} $ ,$ 0.05\, {\rm{GeV}} $ , and$ 0.07 \,{\rm{GeV}} $ .Finally, the melting diagram of the quark-antiquark pair in both
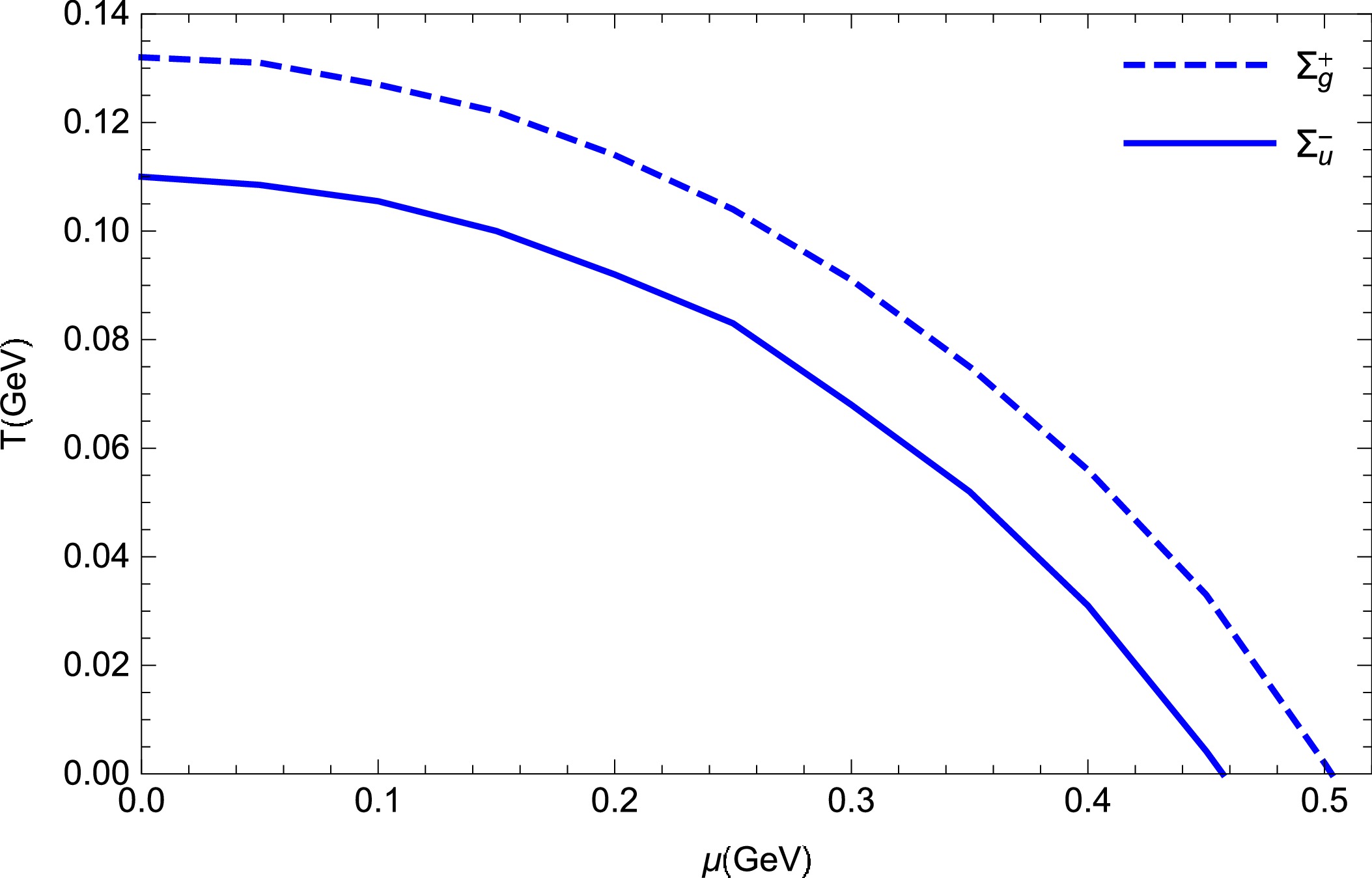
$ \Sigma_g^+ $ ground state and$ \Sigma_u^- $ excited state is shown in Fig. 8. The melting line of$ \Sigma_u^- $ is lower than that of$ \Sigma_g^+ $ . It can be inferred from this melting diagram that the$ \Sigma_g^+ $ ground state is more stable than the$ \Sigma_u^- $ excited state. -
Heavy ion collisions can generate extremely high temperatures and densities in a very short amount of time. We mainly studied the exotic hybrid pseudopotentials at finite temperature and chemical potential. To this end, we used a string configuration for the
$ \Sigma_u^- $ hybrid meson proposed by Oleg Andreev in Refs. [61, 64]. In particular, in this study we focused on the influence of temperature and chemical potential on$ \Sigma_g^+ $ and$ \Sigma_u^- $ hybrid pseudopotentials. At short distances, the$ \Sigma_u^- $ hybrid pseudopotential at finite temperature and chemical potential no longer exhibits a Coulomb-like behavior but seems to exhibit a quadratic function of the separate distance. It behaves linearly at long ranges, just as a$ \Sigma_g^+ $ pseudopotential. There exist significant differences between the excited and ground states. In addition, we found that the screen distance and hybrid pseudopotential of$ \Sigma_u^- $ significantly decrease as the temperature and chemical potential increase. However, temperature and chemical potential effects have a minor impact on the$ \Sigma_g^+ $ pseudopotentials. Finally, the melting diagram in the$ T - \mu $ plane shows that the quark-antiquark pair in the excited state is more likely to melt.We provide an approach to understand the
$ \Sigma_u^- $ hybrid pseudopotentials at finite temperature and chemical potential. The hybrid (pseudo)potentials of other hybrid mesons and baryons deserve further study in the future. Moreover, we will consider the impact of some extreme conditions (e.g., rotating matter and magnetic field) on the hybrid (pseudo)potentials.
Exotic hybrid pseudopotentials at finite temperature and chemical potential
- Received Date: 2024-08-28
- Available Online: 2025-01-15
Abstract: Using gauge/gravity duality, we studied the exotic hybrid pseudopotentials at finite temperature and chemical potential. The Σ hybrid meson can be described by a model including an object called "defect'' on a string linking the quark and antiquark. The






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: