Invariant mass spectroscopy of ¹⁵C

Nuclear clustering is a fascinating and important phenomenon in nuclear physics, where owing to many-body correlations, nucleons (protons and neutrons) within an atomic nucleus bunch up to form substructures or clusters. These clusters can exhibit properties similar to smaller nuclei, such as alpha particles, $ ^{12} {{\rm{C}}}$, or other light nuclei. Owing to their strong binding energy, alpha particles are the most common building blocks of nuclear clustering. As early as 1931, Gamow proposed that 4n-nuclei such as $ ^8 {{\rm{Be}}}$, $ ^{12} {{\rm{C}}}$, and $ ^{16} {\rm{O}}$ were composed of alpha particles [1]. Such models of nuclei with alpha particles as the main constituents remained the mainstream [2, 3] for a long time after the discovery of the neutron in 1932 [4], notwithstanding the early emergence of the model for independent particle motion [5]. It was not until 1949 after the development of the more robust nuclear shell model [6, 7] that the independent-particle picture became the dominant nuclear model.

The prediction [8] and discovery [9] in the 1950s of the famous resonance Hoyle state – a triple-alpha clustering state – in $ ^{12} {{\rm{C}}}$ at 7.65 MeV reaffirmed the importance of alpha clustering. The introduction of the Ikeda diagram [10] a decade later provided useful guides for the observation of cluster states in excited states of light nuclei, particularly near their alpha-decay threshold. Since then, experiments have been performed to search for alpha-clustering states in stable [11−14], as well as in exotic nuclei, where excessive valence neutron(s) or proton(s) may lead to the formation of molecular states [15−23]. Because of the subtle interplay between many-body correlations and single-particle behavior, which leads to competition between alpha-clustering and single-particle structures, experimentally identifying the clustering states from a multitude of single-particle states remains challenging.

Invariant mass spectroscopy is an effective tool for studying nuclear resonance states in nuclear physics, particularly under inverse kinematics conditions using radioactive ion beams [20−22, 24−28]. These are excited states of nuclei that typically decay rapidly (on the order of $ 10^{-22} $ to $ 10^{-15} $ s) by emitting particles such as alpha or gamma rays. By analyzing the invariant mass of the decay products, the properties of these resonances, such as their mass, width, and decay modes, can be determined, providing insights into the nuclear structure and the underlying nuclear forces, nuclear reaction dynamics, and stellar nucleosynthesis. For a resonance state that decay by emitting a nuclear cluster such as alpha particles, measurements of the decay alpha particle and residual nucleus provide access to the resonance parameters.

An ideal reaction for studying nuclear resonance states, particularly those involving clustering or other exotic structures, typically consists of two key steps: population of resonance states and resonant decay. However, in reality, prompt particles from direct breakup are always present, resulting in physical backgrounds. Therefore, accurate estimates of the background from non-resonant components are essential to extracting resonance parameters from invariant-mass spectra. Presently, no methods have been established to evaluate such contributions. One of the conventional methods for estimating the contribution is the event-mixing method. However, it does not provide a satisfactory level to describe the spectrum. The result with such event mixing often overestimates the non-resonant background, particularly near the charged particle threshold, owing to the difficulty of treating the long-range Coulomb final-state interactions, which are not included in the event-mixing analysis. A phenomenological weighted event-mixing method has recently been proposed to address this problem [29].

In this article, we report on an invariant-mass spectroscopy employing the $ ^{208} {\rm{Pb}}$($ ^{15} {{\rm{C}}}$, $ ^{15} {{\rm{C}}}^*$ $ \rightarrow $ $ ^{11} {{\rm{Be}}}$+$ ^4 {{\rm{He}}}$) reaction to search for resonance state(s) in $ ^{15} {{\rm{C}}}$ at excitation energies above the alpha-decay threshold of 12.73 MeV [30]. Most of the studies on the clustering effect in neutron-rich carbon isotopes have focused on the neighboring$ ^{14,16} {{\rm{C}}}$. Several spectroscopy studies on $ ^{15} {{\rm{C}}}$ have been reported [31−33], but the discussions focus on single-particle resonances. In this paper, to address the problem of overestimation of the non-resonant background, we refer to the Gamow theory of alpha decay [1] and introduce a new method that aims at a robust treatment of the Coulomb effect. Combined with the phenomenological weighted event-mixing method [29], our analysis results suggest possible resonant states in $ ^{15} {{\rm{C}}}$. A brief description of the experiment is given in Sec. II. Next, detailed descriptions of the analysis procedures, which include non-resonant background estimation, spectrum fitting, and a brief discussion on the results are given in Sec. III. Finally, a summary is given in Sec. IV.

The experiment was performed at the Radioactive Ion Beam Line of the Heavy Ion Research Facility in Lanzhou (HIRFL-RIBLL) [34, 35]. Secondary beams were produced via the projectile fragmentation reaction using a 60-MeV/nucleon $ ^{18}{\rm{O}} $ primary beam incident on a 4.5-mm-thick $ ^{9}{{\rm{Be}}} $ target. Following subsequent magnetic-rigidity selection and purification by RIBLL, a secondary beam of $ ^{15} {{\rm{C}}}$ at about 27.9 MeV/nucleon with an average intensity of approximately 2.0$ \times 10^4 $ particles per second (pps) and a purity of approximately 81% was obtained. The beam particle identification was achieved by combining the magnetic rigidity ($ B_\rho $), time-of-flight (TOF), and energy loss ($ \Delta E $) on an event by event basis. The TOF was provided by two 50-µm thick plastic scintillation detectors installed at the second (T1) and fourth (T2) achromatic focal planes of RIBLL, which are approximately 17 m apart. A large area silicon detector was installed near the T2 focal plane to measure the energy loss. Three position-sensitive parallel plate avalanche counters (PPACs), with a typical position resolution of approximately 1 mm (FWHM), located upstream of the target, were used to track incident beam particles.

The $ ^{15} {{\rm{C}}}$ beam bombarded a 230-mg/cm²-thick $ ^{208} {\rm{Pb}}$ target with a size of 30 mm in diameter to induce inelastic scattering populating unbound cluster states in $ ^{15} {{\rm{C}}}$, namely, $ ^{208} {\rm{Pb}}$($ ^{15} {{\rm{C}}}$, $ ^{15} {{\rm{C}}}$$ ^\star \rightarrow $ $ ^{11} {{\rm{Be}}}$ + $ ^4 {{\rm{He}}}$). A zero-degree telescope called T0, which forms one part of a larger detection system described in detail in Refs. [22, 36, 37], was employed to coincidentally detect the charged reaction products. The telescope was placed symmetrically with respect to the beam axis at a distance of approximately 170 mm downstream of the target, thus providing an approximate angular coverage range of $ \pm $10.7° as observed from the center of the $ ^{208} {\rm{Pb}}$ target. The T0 telescope consists of three 1000-µm-thick double-sided silicon strip detectors (DSSDs), three 1000-µm-thick segmented single-readout silicon detectors (SSDs), and four CsI(Tl) crystals arranged in a 2$ \times $2 matrix, and readout by photodiodes. The DSSDs and SSDs have an active area of 64 mm$ \times $64 mm; each side of a DSSD has 32 strips with a strip width of approximately 2 mm. In the present experiment, the charged reaction products, namely, $ ^{11} {{\rm{Be}}}$ and alpha, did not reach the CsI(Tl) detectors; the $ ^{11} {{\rm{Be}}}$ nuclei stopped in one of the DSSDs, whereas the alpha particles either stopped in or penetrated the DSSDs, depositing a portion of their kinetic energies, before being stopped in one of the SSDs.

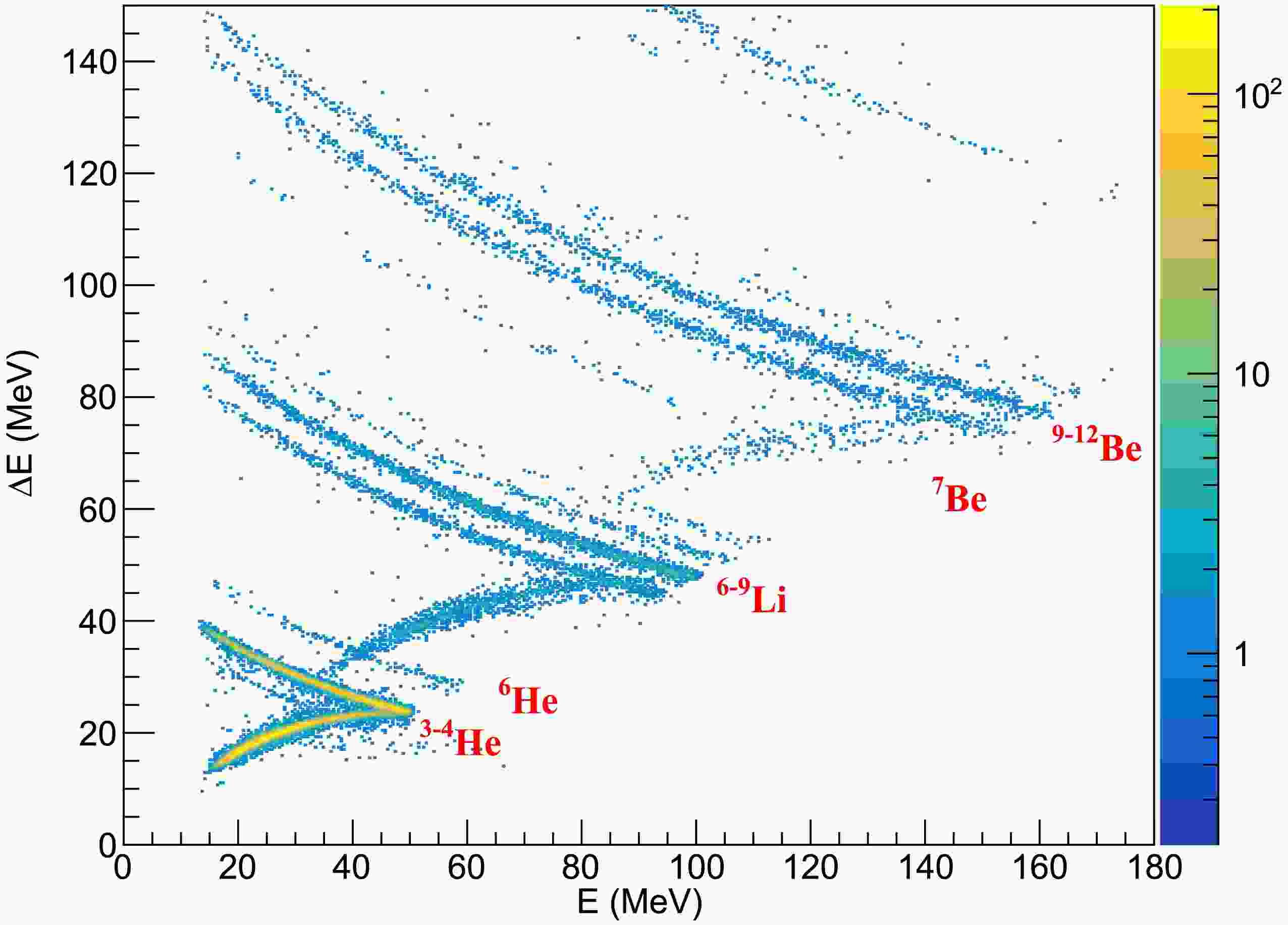
The energy of the DSSDs was calibrated through a combination of normalization and calibration procedures. First, the signals of different strips on both sides were normalized using the method described in Ref. [38]. The absolute energy calibration was achieved by combining the measurement with an $ ^{241} {\rm{Am}}$ standard alpha particle source and the threshold energies of nuclei penetrating each DSSD. For the SSD, only absolute energy calibration was performed. The average relative energy resolution of silicon detectors was approximately 1% at 5.486-MeV alpha-particle energy, obtained with the $ ^{241} {\rm{Am}}$ source. For the energy calibration of CsI(Tl) crystals, a linear formula for He isotopes was used, which is a reasonable approximation, as discussed in Refs. [39, 20, 21]. Unreacted $ ^{15} {{\rm{C}}}$ beam particles, which had several orders higher intensity than the reaction products, penetrated the first layer of the T0 telescope and were stopped in the second layer of the DSSDs. To exclude accidentally coincident events due to these beam particles, we considered timing signals of the DSSD strips on the both sides. The horizontal (X) and vertical (Y) positions of two coincident particles on each DSSD were determined by matching their energy signals at the front and rear sides. Reaction particles produced by the $ ^{15} {{\rm{C}}}$ beam impinging on DSSDs were mostly removed by considering correlating hits with consistent positions on the target and at least two adjacent DSSDs [20−22]. After the above-mentioned analysis procedure, a clean particle-identification (PID) plot was obtained based on the energy loss versus residual energy ($ \Delta E $-E) technique, as shown in Fig. 1. Assuming that the reaction occurred at the center of the target, the kinetic energies of the reaction products, namely, $ ^{11} {{\rm{Be}}}$ and alpha, immediately after the reaction were determined with consideration of their energy losses in the target. The momenta of $ ^{11} {{\rm{Be}}}$ and alpha were then determined considering their scattering angles.

Figure 1.  (color online) $\Delta E$-E spectrum. $\Delta E$ and E represent the energy losses of charged particles in the first and second layers of the DSSDs of the T0 telescope, respectively.

The excitation energy spectrum of $ ^{15} {{\rm{C}}}$ was reconstructed using the momenta and rest masses of the coincidentally detected $ ^{11} {{\rm{Be}}}$ and alpha employing the invariant mass method. Because $ ^4 {{\rm{He}}}$ does not have bound excited state, whereas $ ^{11} {{\rm{Be}}}$ has only one with an excitation energy of 0.32 MeV, $ ^{11} {{\rm{Be}}}$ may be in its ground or bound excited state. Because the invariant-mass resolution of the present experiment did not allow the separation of the ground and excited states in $ ^{11} {{\rm{Be}}}$, in the following analysis, we assume that all $ ^{11} {{\rm{Be}}}$ particles measured coincidently with $ ^4 {{\rm{He}}}$ were in the ground state.

For cluster decay following nuclear reaction $ ^{208} {\rm{Pb}}$ ($ ^{15} {{\rm{C}}}$, $ ^{15} {{\rm{C}}}^*$ → $ ^{11} {{\rm{Be}}}$ + $ ^{4} {{\rm{He}}}$), the excitation energy of $ ^{15} {{\rm{C}}}^*$ is expressed as follows:

where $ m_{^{15}{\rm{C}}} $ is the rest mass of $ ^{15} {{\rm{C}}}$, and $ m_{^{15}{\rm{C}}^*} $, $ E_{^{15}{\rm{C}}^*} $, and $ P_{^{15}{\rm{C}}^*} $ are the rest mass, total energy, and momentum of the resonant nucleus $ ^{15} {{\rm{C}}}$$ ^* $, respectively. Here, we have adopted the natural unit for the speed of light, i.e., $ c = 1 $. According to the conservation of energy and momentum during the decay process, $ E_{^{15}{\rm{C}}^*} $ and $ P_{^{15}{\rm{C}}^*} $ can be calculated using

For each breakup fragment, the total energy, momentum, and kinetic energy are related as follows:

where i represents $ ^{11} {{\rm{Be}}}$ or $ ^{4} {{\rm{He}}}$, and $ P_i $ and $ T_i $ represent their momentum and kinetic energy, respectively. Combining Eqs. (2), (3), (4), (5), and (6), we can deduce $ m_{^{15}{\rm{C}}^*} $ as

The kinetic energies and opening angle (θ) of the two fragments produced from $ ^{15}{\rm{C}}^* $ were measured in the experiment, whereas the ground-state rest masses are taken from Ref. [40]. Hence, $ m_{^{15}{\rm{C}}^*} $ can be reconstructed using experimental kinetic energies ($ T_{^{11}{\rm{Be}}} $ and $ T_{^{4}{\rm{He}}} $) and the angular information of the two coincident products. The excitation energy can also be expressed as

where $ E_{\rm{th}} $ is the threshold energy of the decay.

A Monte-Carlo simulation was conducted to evaluate the detection efficiency and invariant-mass resolution, taking into account (i) the geometry and performances of the detectors, which include the active area of the DSSDs, strip width, and energy resolution; (ii) the energy and angular spread of the beam; and (iii) the reaction position and energy loss of the beam and fragments in the target. Figure 2 shows the detection resolution and efficiency as functions of the relative energy for $ ^{15} {{\rm{C}}}$ decaying into $ ^{11} {{\rm{Be}}}$(g.s.) + $ ^{4} {{\rm{He}}}$.

Figure 2.  (color online) Simulated detection resolution (left) and efficiency (right) as functions of the relative energy for ¹⁵C decaying into ¹¹Be(g.s.) + ⁴He, respectively.

As in most invariant-mass spectroscopy measurements involving unbound resonance states, reconstructed spectra are likely to include non-resonant contributions in addition to resonant states. To estimate the non-resonant contribution, we applied the event-mixing method. Following the prescription proposed in Ref. [29], we employed the following functional form to estimate the reduction factor:

where $ c_1 $ and $ c_2 $ are the parameters to determine each final state, and $ E_R $ is the relative energy for the two-cluster system. For example, $ c_1 = -38.4 $ MeV and $ c_2 $ = +1.19 MeV were used for the p+$ ^8 {\rm{B}}$ channel [29].

In this paper, we introduce another method that focuses on a robust treatment of the Coulomb effect, which is frequently applied to describe alpha-decay processes [1]. The penetrability P of alpha particles in a Coulomb barrier is formulated as follows:

where $ Z_1 $ and $ Z_2 $ are the atomic numbers of the two clusters, respectively, µ and E are the reduced mass of the clusters and total decay energy of a resonance, respectively, R is the radius of the nuclear potential, and b is the outer radius of the Coulomb barrier at energy E. The penetrability is a function of the total decay energy and is introduced as a reduction factor in the event-mixing method. Because $ E_R $ is equal to E in the present case, $ P(E) $ is taken as equal to 1+R(E) by definition here. It is analytically solved using the sharp-cut Coulomb barrier method, namely,

Here, $ B_{\rm{C}} $ is the energy height of the Coulomb barrier at radius R. Conventionally, R is taken as the sum of radii of the two clusters:

where $ A_1 $ = 11, $ A_2 $ = 4, and $ r_0 $ typically takes a value of 1.40 fm. Although the event-mixing method can explain the spectrum at larger decay-energy region, we found that the penetrability with conventional R with $ r_0 = $1.40 fm underestimated the spectrum near the threshold. Hence, we introduce additional degrees of freedom to reproduce the shape of the spectrum. Parameter R is randomly determined assuming a normal distribution with its mean value and width as the new free parameters. Typically, an approximately 50% larger mean value than the usual radius R is necessary. In the present $ ^4 {{\rm{He}}}$+$ ^{11} {{\rm{Be}}}$ channel, a 2.0 fm larger value than the conventional R and a width of 3.5 fm (in σ) were adopted. In Fig. 3, we compare the mixed-event distribution without (red histogram) and with reduction correction obtained with different methods. The blue and black histograms are the weighted mixed events corrected with the sharp-cut and effective Coulomb barrier methods, respectively.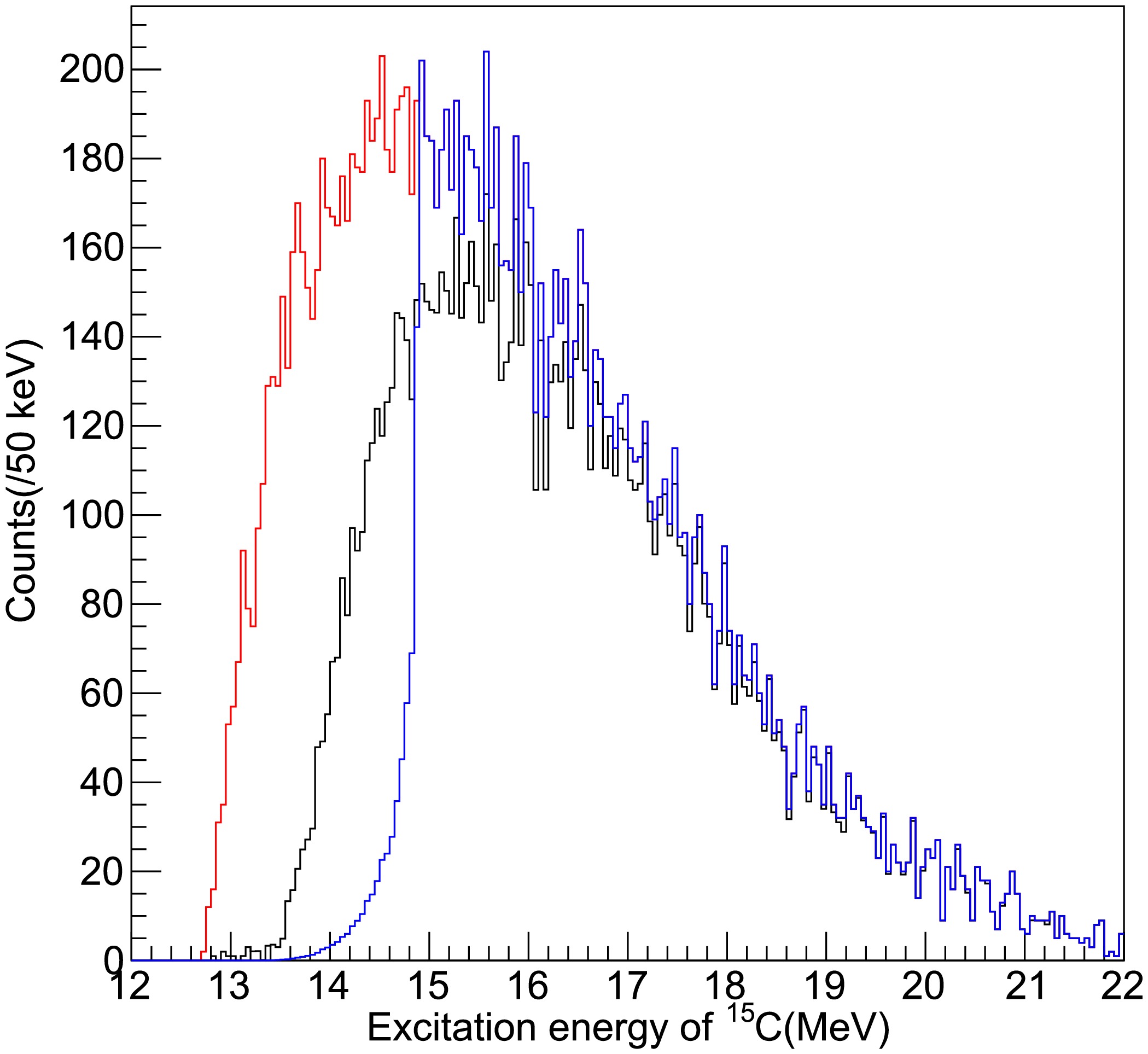

Figure 3.  (color online) Excitation energy spectrum with the background distribution produced by the event-mixing analysis coupled to the reduction factors deduced using two different methods. The red histogram represents the mixed-event distribution without any reduction correction, whereas the blue and black histograms are the weighted mixed events corrected with the sharp-cut and effective Coulomb barrier methods, respectively.

Figure 4 shows the reduction factor as a function of the total decay energy obtained with the present effective Coulomb barrier method. For comparison, the reduction factor obtained with the phenomenological method in Ref. [29] but for the case of p+$ ^8 {\rm{B}}$ is also shown as the red histogram. Both distributions exhibit a similar trend moving towards the particle threshold, starting to deviate at around a few megaelectronvolts above the threshold and gradually decreasing to zero. Because the statistics in this study are very limited, following the recipes in Ref. [29] to determine parameters $ c_1 $ and $ c_2 $ using the present data is very challenging. For a practical reason, we analyzed the ''1+R'' correlation function data for the $ ^3 {{\rm{He}}}$+ $ ^8 {\rm{B}}$ channel in Ref. [29], whose Coulomb barrier is close to the present $ ^4 {{\rm{He}}}$+$ ^{11} {{\rm{Be}}}$ channel, and obtained $ c_1 $ = +2.017 MeV and $ c_2 $ = +0.482 MeV for the reduction factor. The reduction factor was then adopted to estimate the non-resonant background.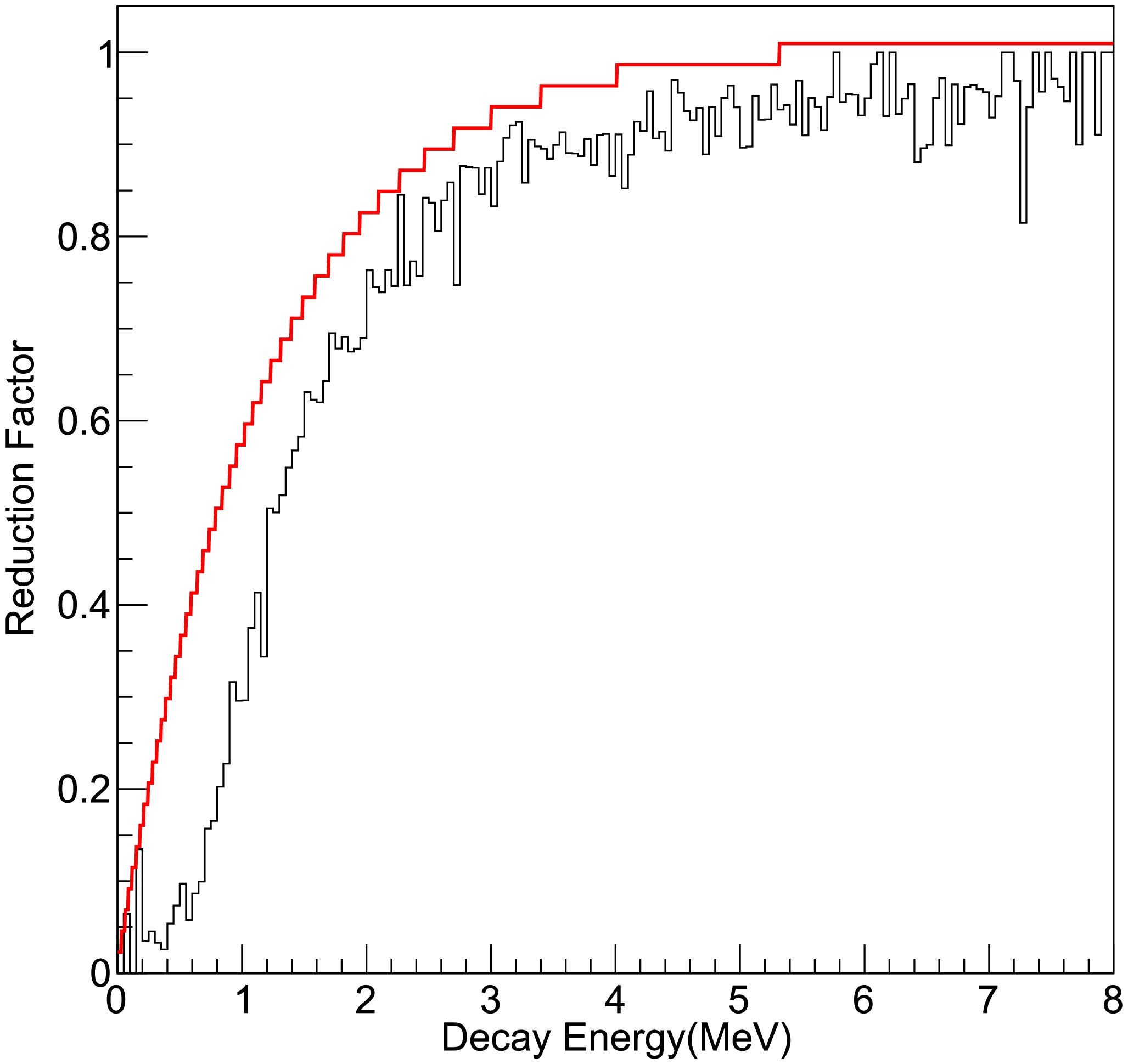

Figure 4.  (color online) Reduction factor as a function of the total decay energy. The black and red histograms represent the results of the present method for ⁴He+ ¹¹Be and the method from Ref. [29] for the p+ ⁸B channel, respectively. Both distributions exhibit a similar trend moving towards the particle threshold, starting to deviate at around a few megaelectronvolts above the threshold and gradually decreasing to zero.

We describe the background distribution using the event-mixing data obtained in the present work coupled with the decay-energy dependent reduction factor determined with two different methods. For simplicity, we fitted the event-mixing data using a sixth-order polynomial function. The amplitude of the distributions was then determined to reproduce the events at the excitation energy above 17 MeV in the excitation-energy spectrum. The resonance state can be described by a convoluted function of a Breit-Wigner distribution with the decay-energy-dependent experimental resolution function in the Gaussian form. This was achieved by using the Voigt function provided by the ROOT library [41]. Because the typical resolution at 2 MeV decay energy is 250 keV in σ and is much larger than that expected for a resonance state, the spectrum shape of the resonance states is expected to be nearly Gaussian, and their widths are primarily determined by the experimental resolution described above. Figure 5 shows the excitation energy spectrum, along with the weighted event-mixing background distributions obtained with the above-mentioned two different methods. The black background, obtained with the effective Coulomb barrier method reproduces the experimental data well with a reduced chi-square $ \chi^2 /ndf = $ 43.3/35. The second type of background, the magenta histogram, obtained with the mixed events incorporating the reduction factor (Eq. 9) with $ c_1 $ = +2.017 MeV and $ c_2 $ = +0.482 MeV, exhibits a reduction in the lower energy region. We note that a small energy shift of approximately 100 keV has been introduced to the distribution to compensate for the difference in the Coulomb barrier between the $ ^4 {{\rm{He}}}$+$ ^{11} {{\rm{Be}}}$ and $ ^3 {{\rm{He}}}$+$ ^{8} {\rm{B}}$ channels. For convenience, we refer to the weighted event-mixing background obtained with this latter method as ''phenomenologically-corrected background'' (labelled simply as ''bg₂''); the background obtained using the effective Coulomb barrier is referred to as ''Coulomb-corrected background,'' (labelled simply as ''bg₁'') hereinafter.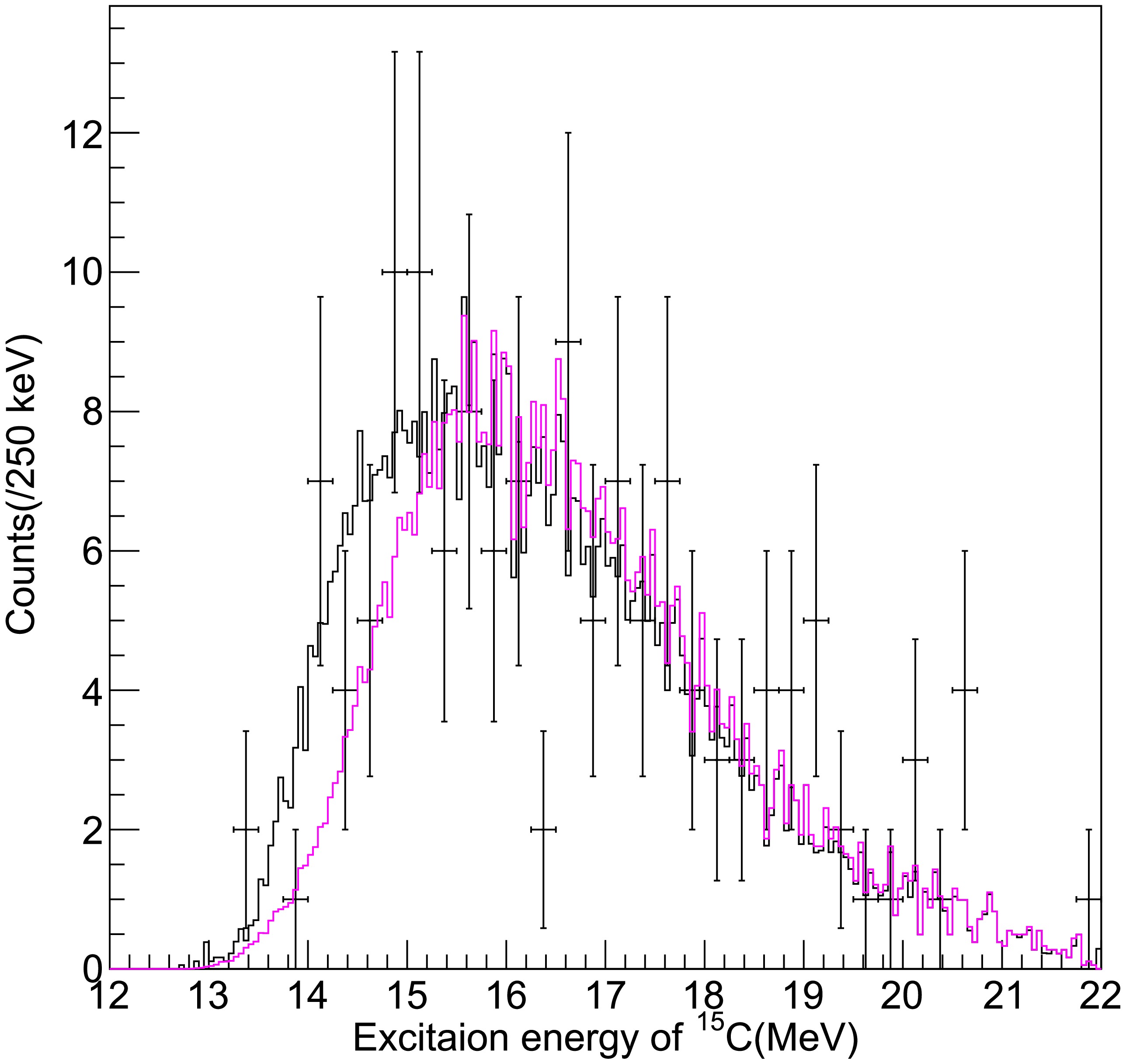

Figure 5.  (color online) Excitation energy spectrum with the background distribution produced by the event-mixing analysis coupled to the reduction factors deduced using two different methods. The black histogram represents the background obtained with the effective Coulomb barrier method, whereas the magenta histogram is the background obtained with the mixed events incorporating the reduction factor given by Eq. (9) with $c_1$=+2.017 MeV and $c_2$=+0.482 MeV.

A few events can be observed on top of the estimated non-resonant background. We consider possible resonance state(s) with signal function(s) of the Voigt form. Figure 6 shows the fitting results (red lines) with possible resonance state candidate(s) (blue lines) plus the two different backgrounds (black histograms). Although the fit with the Coulomb-corrected background describes the experimental data well, a resonance state candidate is suggested at approximately 15 MeV. In contrast, fitting with the phenomenologically-corrected background implies possible observation of two resonance state candidates.

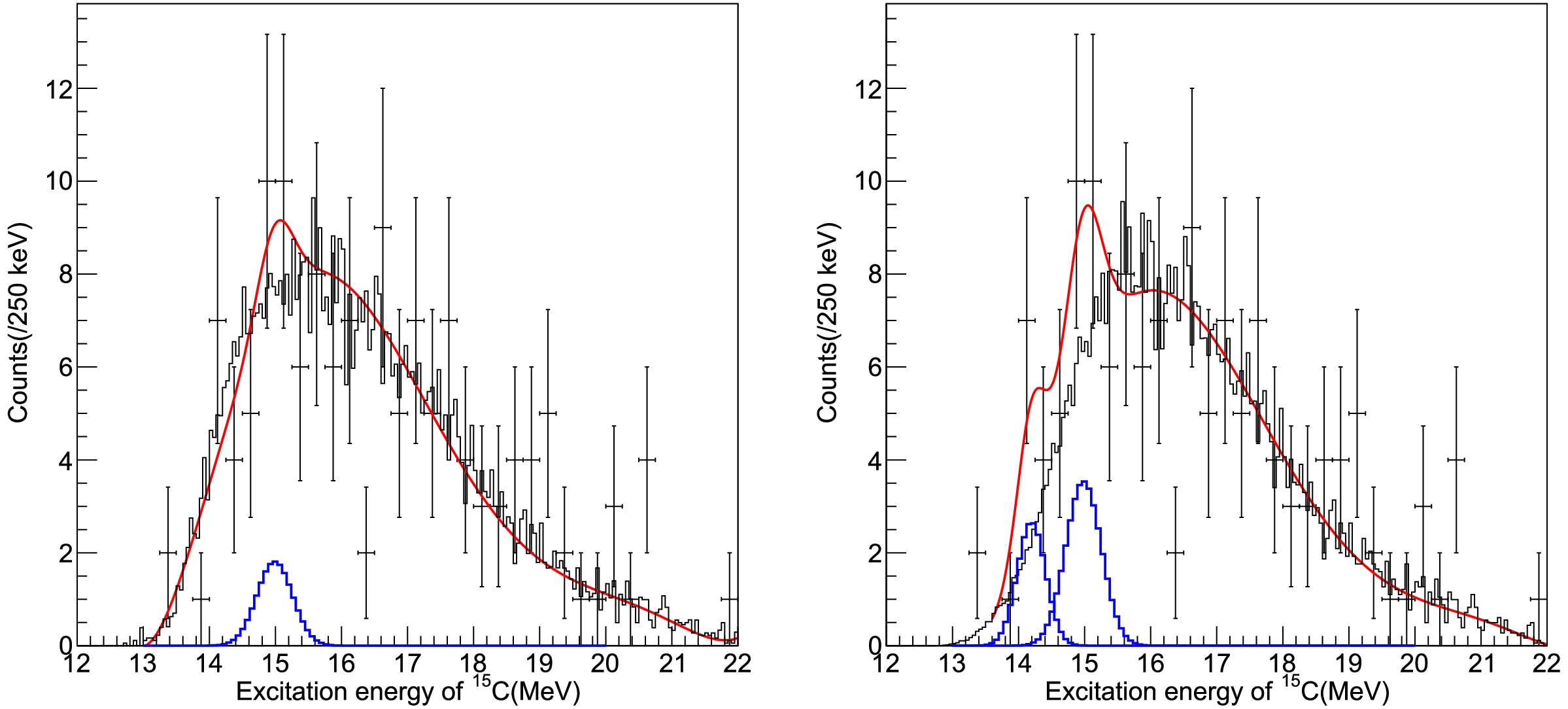
Figure 6.  (color online) Results of spectral fitting (red lines) assuming one (left) and two (right) resonance state(s) (blue lines) plus the event-mixing backgrounds (black histograms) obtained with the effective Coulomb barrier method and the method proposed in Ref. [29], respectively. The experimental resolutions have been assumed for the resonance state candidates.

Further optimization was performed by applying the unbinned maximum likelihood analysis. We define the total probability density function ($ pdf $) consisting of several sub-$ pdf $s. The log-likelihood function is defined as

where $ N_f = 3 $ corresponds to two signal functions and one background distribution considered in the analysis, and n represents the number of data. $ \vec{p}_j $ denotes arrays with dimensions equal to the number of parameters for the respective functions $ f_j $, i.e., dimension = 2 for the signal functions and 7 for the background, although some of the background parameters were fixed during the analysis process. All of parameters $ \vec{p}_j $ and the integral of each sub-$ pdf $ $ \mu_j $ were optimized to maximize log-likelihood function $ \ln L $. The values extracted from the present data are summarized in Table 1. Small differences in the table were observed, potentially owing to the binning bias. The effect of the finite binning size is difficult to avoid because of very limited statistics.

		$\mu_1$	$E_1$	$\Gamma_1$	$\mu_2$	$E_2$	$\Gamma_2$
bg1	binned	4.9(54)	14.99(13)	<0.01	–	–	–
	unbinned	18.3(61)	15.06(15)	<0.01	–	–	–
bg2	binned	9.8(55)	14.98(16)	<0.01	5.7(36)	14.19(12)	<0.01
	unbinned	17.4(60)	15.05(14)	<0.01	8.1(40)	14.22(13)	<0.01

Table 1.  Summary of the extracted values for the two resonant-state candidates. The unit of amplitude $\mu_i$ ($i=1,2$) is count, whereas that of mean $E_i$ and width $\Gamma_i$ is MeV.

The fitting results with both background models indicate a possible structure at approximately 15 MeV although the statistical significance is not high, namely, 0.8 σ and 1.8 σ. The estimated widths Γ of the resonance states are very small, less than one-tenth compared with the experimental resolutions. Therefore, the sensitivity of the natural width in the present analysis is not high. We set the upper limit for the width as 50 keV. The possible states with the second background model have more significance. In addition to the resonance state at 15 MeV, a smaller component of approximately 14 MeV is suggested.

Very limited data exist for $ ^{15} {{\rm{C}}}$ at excitation energies above the alpha particle threshold. Bohlen et al. have reported results from a multi-nucleon transfer reaction at the Hahn-Meitner Institute populating excited states in $ ^{15} {{\rm{C}}}$ up to above the alpha threshold [33]. Several discrete states were observed in the continuum region. Of particular interest is a state with marked intensity at 14.6 MeV, which was assigned a high spin and parity of 11/2⁺. However, this state is not observed in the present analysis. A possible reason for its absence is the difficulty of populating high-spin states by the inelastic scattering. The same reason applies to the other states suggested in that work. The lead target is often used to study electromagnetic $ E1 $ strength through the Coulomb excitation induced by virtual photons. The reaction is well described by a semi-classical theory [42], according to which the number of virtual photons decreases rapidly as a function of the beam energy. Therefore, it is unlikely to populate high excited states in $ ^{15} {{\rm{C}}}$ via the Coulomb excitation. However, such high excited states can be reached via nuclear excitation with the lead target acting as an isoscalar probe. Because the spin-parity of the ground state of $ ^{15} {{\rm{C}}}$ is 1/2⁺, we can intuitively consider the two resonance state candidates observed in this work as clustering states with spin-parities 1/2⁺ and 3/2⁺, populated through $ L = 0 $ or 2 transition.

Recently, a systematic study on cluster states in $ ^{14} {{\rm{C}}}$ was reported using the same experimental technique, but with coincident detection of alpha and $ ^{10} {{\rm{Be}}}$ [22]. Several states above the threshold were identified as members of a cluster band and assigned spin-parities of 0⁺, 2⁺, and 4⁺. Although our statistics are limited and the significance is low, the ''peak'' positions of our observed candidates are closed to the peak positions of those states in $ ^{14} {{\rm{C}}}$. Naively, the simplest and plausible configuration is that of one neutron in the $ s_{1/2} $ orbit coupled to those states in $ ^{14} {{\rm{C}}}$. The weak population of these states in the present experiment may be attributed to competition from neutron-decay channels and the energy landscape of the nuclei involved. For $ ^{15} {{\rm{C}}}$ and its alpha-decay residual $ ^{11} {{\rm{Be}}}$, a neutron-halo nucleus, the relatively small neutron separation energies ($ S_n $ = 1218.1 keV and 501.64 keV [30], respectively) may play a significant role in hindering the population of these resonance states. It will be interesting to perform a further experiment using a light isoscalar target such as $ ^4 {{\rm{He}}}$ or $ {\rm{CD}}_2 $ with about 10 times more statistics and/or perform a theoretical calculation to confirm the resonance states.

We have performed an invariant-mass spectroscopy at HIRFL-RIBLL using the $ ^{208} {\rm{Pb}}$($ ^{15} {{\rm{C}}}$, $ ^{15} {{\rm{C}}}$$ ^\star \rightarrow $ $ ^{11} {{\rm{Be}}}$ + $ ^4 {{\rm{He}}}$) reaction to search for possible resonance states in $ ^{15} {{\rm{C}}}$. By detecting the decay alpha particle and residual $ ^{11} {{\rm{Be}}}$ nucleus in coincidence, we reconstructed the excitation energy spectrum for $ ^{15} {{\rm{C}}}$. To estimate physical background from non-resonant prompt alpha particles, we applied the event-mixing method. Because the prompt alpha's contribution is known to decrease at around the alpha-decay threshold owing to the Coulomb final-state interactions, two methods were employed to determine the reduction factor. The first method employed the recipe proposed in Ref. [29]. To provide a robust treatment of the Coulomb effect, in the second method, we determined the reduction factor based on the Gamow theory of alpha decay. Fitting the spectrum using the background estimated with these two methods, one and two resonance state candidates have been proposed. Further experiments with a light isoscalar target and improved statistics, as well as theoretical calculations, are called for to confirm these resonance states.

The authors thank the accelerator operators for the stable beams throughout the experiment. S.T. appreciates the fruitful discussion on the Coulomb final-state interactions with S. Koyama.