Investigating the shadows of new regular black holes with a Minkowski core: effects of spherical accretion and core type differences

The prediction of BHs by General Relativity (GR) has long been a prominent topic in scientific research, drawing widespread attention and academic debate. Since the Laser Interferometer Gravitational-Wave Observatory (LIGO) first detected gravitational waves from the merger of binary BHs [1−5], LIGO and its partners have recorded nearly a hundred such binary events. These observations not only validate GR but also provide valuable data for BH research. Subsequently, the Event Horizon Telescope (EHT) collaboration released the first ultra-high angular resolution image of the supermassive BH in the Messier 87 (M87*) galaxy, marking a major milestone in astrophysical research [6]. The image revealed a bright ring-like structure surrounding a central dark region, known as the BH shadow, which is formed by light being strongly bent and focused as it approaches the edge of the BH. This ring-like structure is referred to as the photon ring. The strong gravitational field around the BH plays a key role in the formation of the shadow. Furthermore, polarization measurements reported by the EHT have shown the significant influence of the strong magnetic field at the edge of the BH on the behavior of surrounding matter, confirming that the magnetic field structure around the accretion disk of the M87* BH is consistent with predictions from general relativistic magnetohydrodynamics (GRMHD) models [7]. These findings enhance our understanding of the physical processes around BHs, including matter infall and jet formation. Subsequently, the EHT captured the first hierarchical radio observation image of the Sagittarius A* (SgrA*) BH at the center of our Milky Way galaxy, which is primarily characterized by a bright, thick ring [8]. These observations suggest that the accretion disk may influence the observational characteristics of BH shadows, providing a new perspective for studying them.

Indeed, the theoretical analysis of shadow formation for Schwarzschild BH was proposed even before the EHT was constructed [9]. Here, the photon escaping cone was defined by the impact parameter corresponding to the critical curve, known as the BH shadow. Later, Bardeen examined the D-shaped shadow of Kerr BHs, which results from the dragging effect of a rotating BH on the paths of light rays [10]. Additionally, real astrophysical BHs in the universe are always surrounded by various accretion materials, which are crucial for the observation and imaging of BHs. Consequently, Shakura and Sunyaev proposed a standard thin accretion disk model, assuming that the disks are geometrically thin, optically thick, and in a steady state [11]. This model predicts the disk's geometric configuration, optical properties, and spectral characteristics, providing a theoretical foundation for understanding the fundamental nature and energy release of accretion disks. It also aligns with numerous BH observational phenomena. Using this thin accretion disk model, Luminet simulated the first image of a BH with an emitting accretion disk using a semi-analytic method, visually illustrating the gravitational lensing effect and the formation of the photon ring [12].

However, to more accurately approximate accretion flows around BHs in realistic astrophysical environments, it is necessary to consider magnetic field interactions, which require numerical simulations using GRMHD to generate BH images. It is worth noting that, in most cases, toy models of accretion structures are sufficient to reveal the basic characteristics of BH images and the behavior of strong gravitational fields. In this context, Wald et al. studied radiation from the optically and geometrically thin accretion disk around Schwarzschild BHs, categorizing it into direct, lensed ring, and photon ring components [13]. They found that observed BH images are primarily dominated by direct emissions, with smaller contributions from lensed ring emissions and negligible input from photon ring emissions. The observed appearance of the BH shadow depends on the emission details and morphology of the accretion disk, including the geometry of the emission region, the emission profile, and the optical depth. This initiated a series of research efforts on various toy accretion models for different types of BHs [14−22]. Spherical accretion, as a simplified toy accretion model, has also garnered widespread attention [23−29]. In this model, the size and shape of the BH shadow are primarily determined by the spacetime geometry of the BH rather than by the specific details of the accretion process. Consequently, numerous simulations of various BH shadows have been extensively studied, as demonstrated in the examples and references cited in [30−47]. These studies indicate that the properties of BH shadows are closely tied to the spacetime background, offering a potential method to distinguish BHs in GR from other compact objects or BHs predicted by alternative theories beyond GR.

To avoid the infamous singularity problem, researchers have proposed constructing regular BHs without singularities phenomenologically, either by introducing exotic matter that violates standard energy conditions or through quantum corrections to spacetime geometry [48−58]. Traditional regular BHs, such as Bardeen/Hayward/Frolov BH, have a dS core at their centers. Recently, a new type of regular BHs featuring sub-Planckian curvature was introduced in [59–60]. It is characterized by an exponentially suppressed Newtonian potential and an asymptotically Minkowski core. These new regular BHs can reproduce the metric of Bardeen, Hayward, or Frolov BHs on large scales by choosing different forms of the potential and are derived from the GUP in curved spacetime. Such regular BHs with a Minkowski core have also been reported in [61–62]; however, our understanding of them remains incomplete. Hence, exploring the connection between these new regular BHs and astronomical observations to identify signs or traits indicating that the observed BHs in the cosmos are of the regular type rather than traditional singular BHs has become an intriguing endeavor.

Evidently, at this stage, it is impractical to differentiate between singular and regular BHs by crossing the event horizon or detecting signals from their interiors. Nevertheless, distinctions between these BHs may manifest in external phenomena, such as the photon sphere or the trajectories of massive particles [63−75]. Therefore, in [63], we meticulously examined the photon spheres and marginally stable circular orbits for regular BHs with two distinct cores: the new regular BHs with a Minkowski core and Bardeen/Hayward BHs with a dS core. The results show that the positions of the photon sphere and the marginally stable circular orbits for the compact massive object (CMO) phase with a Minkowski core differ notably from their counterparts in the CMO phase with a dS core. Following this, in [17], we investigated the thin accretion disks of regular BHs with a Minkowski core, which can reproduce Bardeen BH at large scales, and compared them with accretion disks around Bardeen BH with a dS core. The results reveal that the thin accretion disks of these regular BHs with different cores exhibit distinct astronomical optical characteristics.

On this basis, we have extended the work presented in [20] by studying images of these new regular BHs with a Minkowski core under spherical accretion and comparing them with those of traditional regular BHs with a dS core. This provides a theoretical foundation for distinguishing between both types of regular BHs with different cores through astronomical observations. More importantly, in [66], we found that for regular BHs with a Minkowski core, different choices of the potential form result in varying positions of the photon spheres and marginally stable circular orbits in the CMO phase. Additionally, it was observed in [20] that the optical characteristics of Bardeen and Hayward BHs surrounded by thin accretion disks exhibit differences. In particular, Hayward BH exhibits a minimal distance between the innermost region of the direct image and the outermost region of the secondary image, which is expected to serve as a distinguishing feature for identifying Hayward BH. These findings have sparked our interest in exploring whether similar differences exist in the images of the new regular BHs with a Minkowski core under the spherical accretion model, making this a meaningful pursuit.

The paper is organized as follows. In Sec. II, we briefly review the new regular BHs with a Minkowski core, which can reproduce the characteristics of traditional regular BHs on large scales, and compare the behavior of light rays around these regular BHs with different cores using a ray-tracing code. In Sec. III, we detail a study on the shadow and optical appearances of these new regular BHs with a Minkowski core under two types of spherical accretion. In Sec. IV, we compare the shadows of regular BHs with a Minkowski core with those of traditional regular BHs (Bardeen/Hayward BHs) with a dS core. Our conclusions and a discussion are presented in Sec. V.

To avoid singularity, the key for constructing a regular BH at the phenomenological level is to ensure that the Kretschmann scalar curvature remains finite. A new type of regular BH with an asymptotically Minkowski core was proposed in [59]. The metric for this type of regular BHs has the form

where

The gravitation potential $ \psi(r) $ is defined as

The dimensionless parameter $ \alpha_{0} $ is induced by quantum gravity effects ¹. The gravitation potential has an exponentially suppressed form, and the motivation stems from the modification of the standard Heisenberg uncertainty principle due to quantum gravity [76−80].

The dimensionless parameters x and n jointly determine the behavior of the Kretschmann scalar curvature at the core, where they must satisfy the conditions $ n \geq x \geq n/3 $ and $ n \geq 2 $ to ensure the existence of the event horizon and maintain the scalar curvature at sub-Planckian levels. Evidently, as r approaches $ 0 $, the spacetime is dominated by a Minkowski core. Moreover, for certain values of x and n, a one-to-one correspondence can be established between such new regular BHs with a Minkowski core and those with a dS core on large scales [59]. Specifically, for the new regular BHs featuring a Minkowski core, as expressed in Eq. (3), there exists the corresponding traditional regular BHs with a dS core; their gravitation potentials are given by

Note that, on large scales, the new regular BH with parameters $ x = 2/3 $ and $ n = 2 $ corresponds to a Bardeen BH, while that with parameters $ x = 1 $ and $ n = 3 $corresponds to a Hayward BH. This indicates that both types of regular BHs exhibit the same asymptotic behavior on large scales; however, they have distinct cores at their centers. Note also that, for these new regular BHs with a Minkowski core, the quantum gravity effect parameter $ \alpha_0 $ must be within the range $ 0 \leq \alpha_0 \leq 0.73M $ for $ x = 2/3 $ and $ n = 2 $ and within the range $ 0 \leq \alpha_0 \leq 0.98M $ for $ x = 1 $ and $ n = 3 $ to ensure the existence of the horizon. When $ \alpha_0 = 0 $, it returns to the standard Schwarzschild BH.

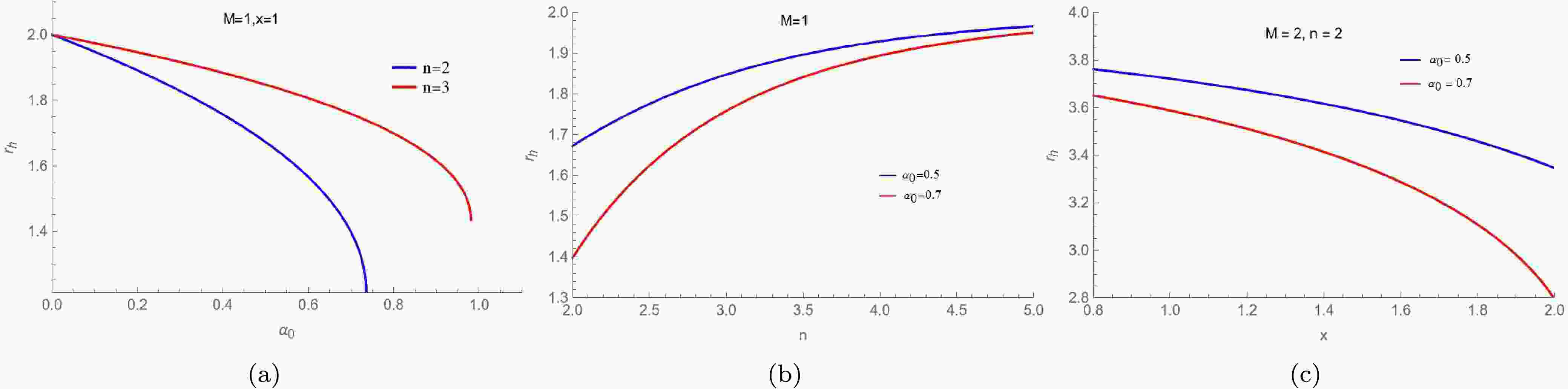
The horizon of the line element expressed by Eq. (1) is determined by solving $ 1+2 \psi(r_h) = 0 $. Following the numerical calculation, we show the influence of the parameters $ \alpha_0 $, n, and x on the event horizon $ r_h $ while keeping the other parameters constant in Fig. 1. Note that the event horizon $ r_h $ decreases as $ \alpha_0 $ increases for fixed n and x. For fixed $ \alpha_0 $, $ r_h $ increases as n increases, but $ r_h $ decreases as x increases.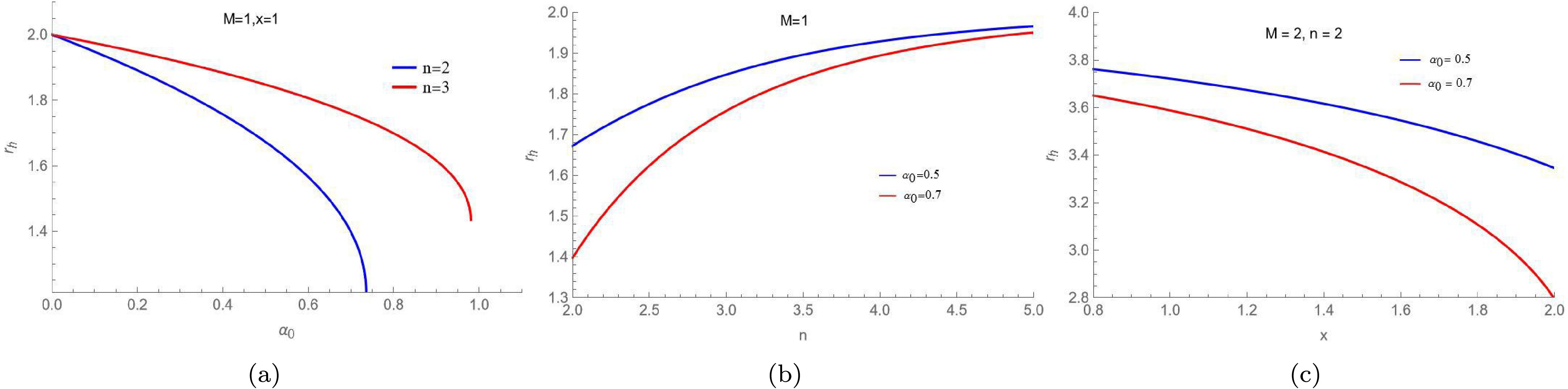

Figure 1.  (color online) Event horizon $ r_h$ of the new regular BHs as a function of the parameters $ \alpha_0$, n, and x.

Next, we examine the motion of photons near these new regular BHs. The motion of these photons is governed by the Euler-Lagrange equation, which is expressed as

Here, λ is an affine parameter, and $ \dot{x}^{\mu} $ represents the four-velocity of the photon. In the context of a static spacetime, the Lagrangian density $ \mathscr{L} $ is expressed as

For photons, the Lagrangian density satisfies $ \mathscr{L} = 0 $. In a spherically symmetric spacetime, we analyzed the motion of photons restricted to the equatorial plane of these new regular BHs by setting $ \theta = \pi/2 $ and $ \dot\theta = 0 $. Given that the Lagrangian density is zero and the metric coefficients cannot be explicitly solved in terms of the t and θ coordinates, there exist two conserved quantities, E and L, representing the energy and angular momentum of the photons, respectively:

By redefining the affine parameter as $ \tilde{\lambda}\to\lambda/|L| $, the four-velocity can be expressed as

Here, the $ \pm $ signs denote the direction of photon motion on the equatorial plane: the ''+'' sign corresponds to clockwise motion whereas the ''−'' sign corresponds to counterclockwise motion. The impact parameter b is defined as

The effective potential $ V_{\text{eff}}(r) $ is expressed as

For null geodesics, where $ g_{\mu \nu} \dot{x}^{\mu} \dot{x}^{\nu} = 0 $, we can obtain the first-order differential equation of motion:

For photons to form a photon sphere, their circular orbit must satisfy $ \dot{r} = 0 $ and $ \ddot{r} = 0 $. Mathematically, this means

Here, $ r_{c} $ represents the radius of the photon sphere, and $ b_{c} $ denotes the corresponding critical impact parameter, which is related to the shadow radius of these new regular BHs.

We present in Tables 1 and 2 the numerical results for the event horizon $ r_h $, photon sphere $ r_c $, and critical impact parameter $ b_c $ corresponding to different values of the parameter $ \alpha_0 $. The results indicate that the values of $ r_h $, $ r_c $, and $ b_c $ for Schwarzschild BH are greater than those of the new regular BHs. For a given $ \alpha_0 $, the values of $ r_h $, $ r_c $, and $ b_c $ for the new regular BHs are related to the spacetime deformation parameters (x and n) and their core type. As the parameter$ \alpha_0 $ increases, the values of $ r_h $, $ r_c $, and $ b_c $ for these new regular BHs decrease. For a given $ \alpha_0 $, the values of $ r_h $, $ r_c $, and $ b_c $ for the new regular BHs are related to the spacetime deformation parameters (x and n) and their core type. When the core type is the same, these values increase with the dimensionless parameters (x and n). This means that, for the new regular BHs, when $ x = 1 $ and $ n = 3 $, their values are greater than those when $ x = 2/3 $ and $ n = 2 $, and the values of Hayward BHs are greater than those of Bardeen BHs. When the dimensionless parameters (x and n) take the same values, the traditional regular BHs with a dS core exhibit slightly greater values than the new regular BHs with a Minkowski core. This discrepancy becomes more significant as the parameter $ \alpha_0 $ increases. This means that Bardeen BH with a dS core exhibit slightly greater values than those with a Minkowski core ($ x = 2/3 $ and $ n = 2 $). Similarly, Hayward BH with a dS core exhibit slightly greater values than those with a Minkowski core ($ x = 2/3 $ and $ n = 2 $).

$ \alpha_0 $	Type	$ r_h $	$ r_c $	$ b_c $
0	Sch	2.00000	3.00000	5.19615
0.3	$ x = 2/3, n = 2 $	1.82833	2.81574	5.00833
	Bardeen	1.83402	2.81929	5.01087
0.72	$ x = 2/3, n = 2 $	1.33657	2.44678	4.66393
	Bardeen	1.49244	2.48965	4.69073

Table 1.  Locations of the outer horizon ($ r_h $), photon sphere ($ r_c $), and impact parameter ($ b_c $) with variation in the deviation parameter $ \alpha_0 $ ($ M = 1 $).

$ \alpha_0 $	Type	$ r_h $	$ r_c $	$ b_c $
0.3	$ x = 1, n = 3 $	1.91656	2.92900	5.13562
	Hayward	1.91849	2.92968	5.13600
0.72	$ x = 1, n = 3 $	1.74762	2.80996	5.03894
	Hayward	1.77024	2.81540	5.04179
0.92	$ x = 1, n = 3 $	1.59272	2.74067	4.98595
	Hayward	1.67020	2.75161	4.99145

Table 2.  Locations of the event horizon, photon sphere, and critical impact parameter of the new regular BHs ($ x = 1, n = 3 $) and Hayward BH for different values of$ \alpha_0 $. We set $ M = 1 $.

For better understanding of how the specific parameters affect the photon trajectories and their classification, we describe the motion of photons around these new regular BHs by tracking the change in the radial coordinate as a function of the azimuthal angle ϕ. By introducing the parameter $ u = 1/r $, we are able to derive the trajectory equation:

The azimuthal angle ϕ can be integrated out as

Based on the above formulae, we numerically simulated the turning points of photon trajectories around the new regular BHs and analyzed the corresponding geodesic geometry. To accurately distinguish among different light trajectories, we used polar coordinates $ (b, \phi) $ and employed a ray tracing code to plot the paths of light as it moves around the new regular BHs, as shown in Fig. 2. These plots represent the changes in trajectories for different values of the impact parameter b, with the separation between these values being $ 0.2 $.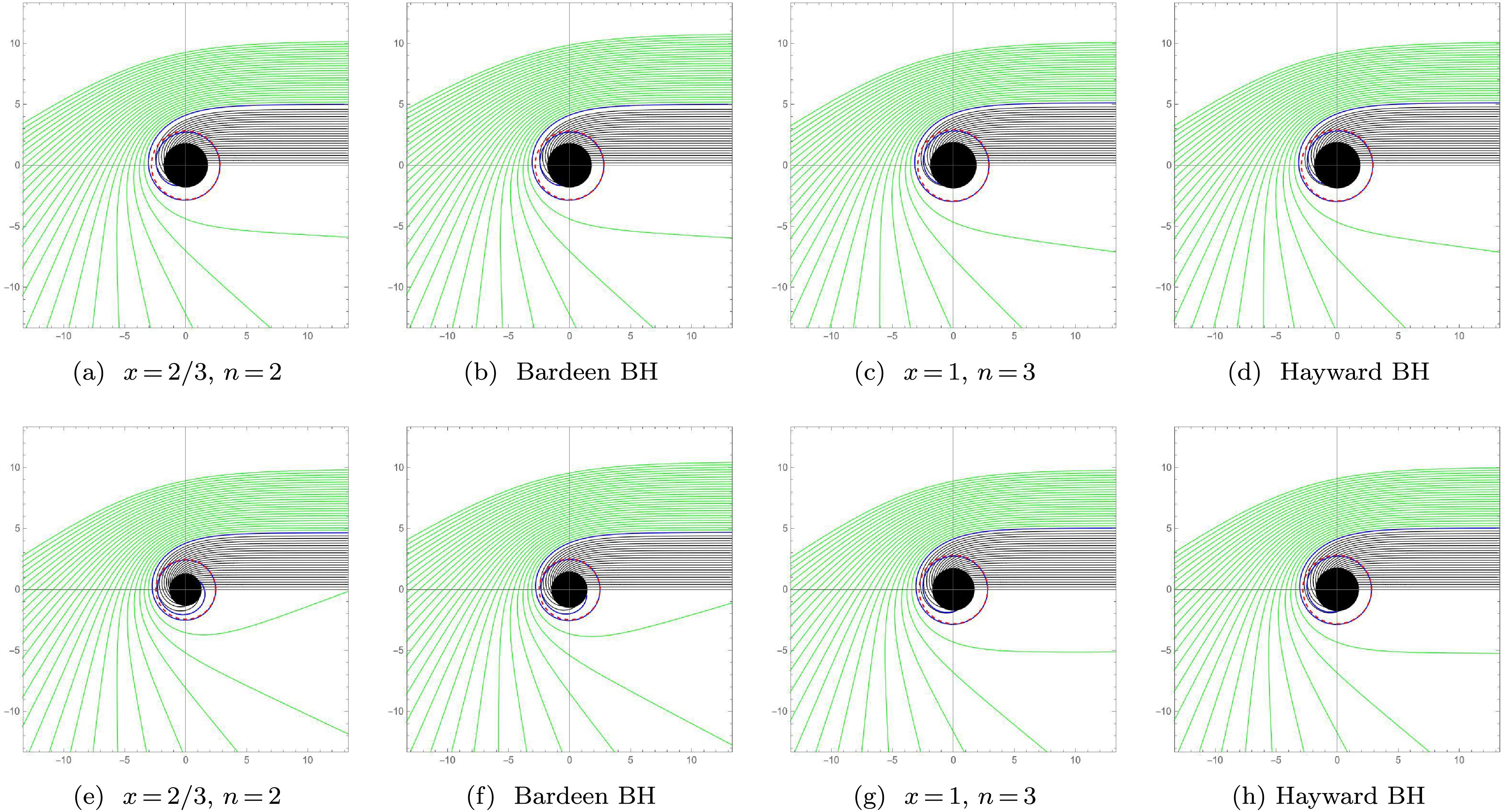

Figure 2.  (color online) Trajectories of light rays for regular BHs with different cores. The top and bottom plots correspond to $ \alpha_0 = 0.3 $ and $ \alpha_0 = 0.72 $, respectively. We set $ M = 1 $.

In Fig. 2, the black disk represents the area inside the event horizon, whereas the red dashed circle denotes the trajectory of light rays with critical parameter $ b = b_c $, which finally forms the photon sphere. For $ b < b_c $, the light trajectories are engulfed by these regular BHs, making them invisible to an observer at infinity, as shown by the black lines in Fig. 2. For $ b > b_c $, the light trajectories are deflected, enabling them to reach an observer at infinity, as shown by the green lines in Fig. 2. Moreover, as the parameter $ \alpha_0 $ increases, the area in which the light trajectories are captured by these regular BHs decreases, as shown in Tables 1 and 2. Additionally, the area in which the light trajectories are captured by these regular BHs is also related to the dimensionless parameters (x and n) and their core type, as shown in Table 1 and 2. Figure 2 shows that, for the same core, the shadow radius of the new regular BHs with parameters $ x = 1 $ and $ n = 3 $ is greater than that with $ x = 2/3 $ and $ n = 2 $, and Hayward BH has a greater shadow radius than Bardeen BHs. For the same dimensionless parameters (x and n), the shadow radius of Bardeen BH with a dS core is slightly greater than that with a Minkowski core ($ x = 2/3 $ and $ n = 2 $), and the shadow radius of Hayward BH with a dS core is slightly greater than that with a Minkowski core ($ x = 2/3 $ and $ n = 2 $).

These results indicate that the changes in the parameters induced by quantum gravity effect (represented by $ \alpha_0 $) and spacetime deformation (characterized by x and n) can modify the radius of these shadows. In particular, as the parameter $ \alpha_0 $increases, the differences in the motion of photons around the new regular BHs with different parameters (x and n) and distinct cores become more evident. This finding offers crucial clues for further research on the impact of quantum gravity and spacetime structure on the images of the new regular BHs presented in the next section under spherical accretion models.

In this section, we investigate the shadow images of the new regular BHs with a Minkowski core, considering two models of spherically symmetric accretion: static and infalling spherical accretions. We examine the impact of the parameter ($ \alpha_0 $) that is induced by quantum gravity effects and the parameter (n) that describes the formation of various spacetime structures on the observational characteristics of the shadow.

Generally, when matter in the universe is captured by a BH, the morphology of the accretion flow around the BH is governed by its angular momentum. High angular momentum causes the matter to form a disk-like accretion structure, whereas extremely low angular momentum leads the matter to flow radially toward the BH, resulting in spherically symmetric accretion [80−86]. We first investigate the shadow images and photon spheres of the new regular BHs with a Minkowski core surrounded by static spherical accretion, assuming that the accretion is static relative to these BHs. For an observer at infinity, the observed specific intensity $I_{\rm obs}(\nu_o)$ (measured in $ \text{erg} $ $ \text{s}^{-1} $ $ \text{cm}^{-2} $ $ \text{str}^{-1} $ $ \text{Hz}^{-1} $) is determined by integrating the specific emissivity along the photon path γ [85–86]:

Here, $ \nu_{o} $ is the frequency of the observed photon, and $ \nu_{e} $ is the frequency of the emitted photon. The redshift factor g is defined as $ g = \nu_{o} / \nu_{e} = f(r)^{1/2} $. In the rest frame of the emitter, $ j_{e}(\nu_{e}) $ represents the emissivity per unit volume and is typically given by the form $ j_{e}(\nu_{e}) \propto \delta(\nu_{r} - \nu_{e}) / r^{2} $, where $ \nu_{r} $ is the frequency in the rest frame of the emitter [86]. The infinitesimal proper length $ {\rm d}l_{\text{prop}} $ is given by

where ${\rm d}\phi /{\rm d} r$ is obtained from Eq. (13). Subsequently, the observed specific intensity is expressed as

According to Eq. (17), the observed specific intensity $I_{\rm obs}$ is a function of the impact parameter b. Note that we aim to study how variations in the quantum gravity effect parameter ($ \alpha_0 $) and spacetime deformation (n) affect the observed specific intensity. We compared the cases with $ x = 2/3 $ and $ n = 2 $ to those with $ x = 1 $ and $ n = 3 $. In Fig. 3, we show the trend of the observed specific intensity at spatial infinity as a function of the impact parameter b. It is evident that the observed specific intensity increases gradually with b when $ b<b_c $, rising sharply as it approaches $ b_c $, reaching a maximum at this position. Following this, as the value of b continues to increase beyond $ b_c $, the observed specific intensity begins to decrease gradually, eventually approaching zero at infinity.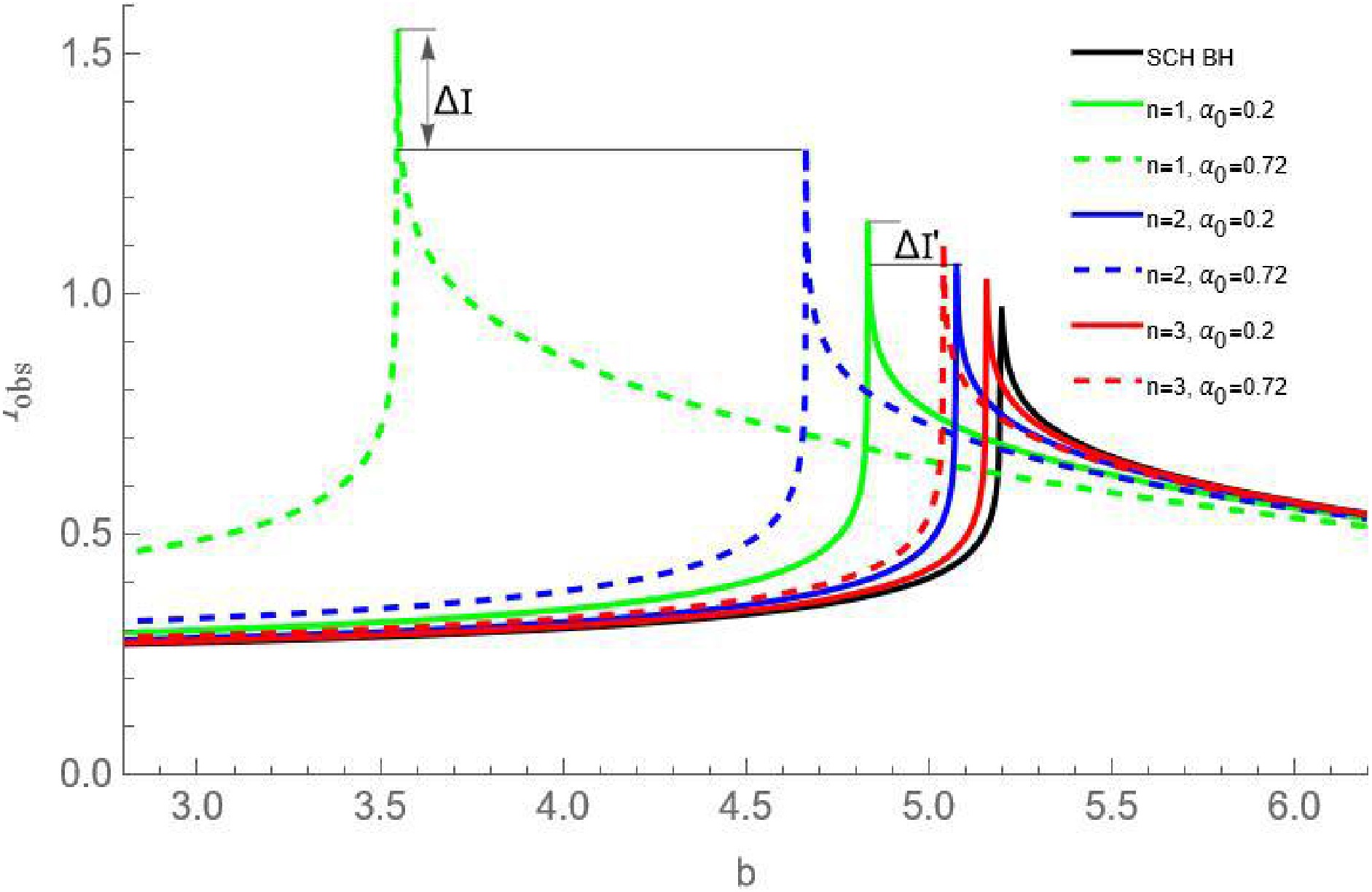

Figure 3.  (color online) Variation of the observed specific intensity radiated from the static spherical accretion with the impact parameter for different values of $ \alpha_0 $ and n. We set $ M = 1 $.

Figure 3 shows that the peak intensity for the new regular BHs with a Minkowski core is consistently higher than that of Schwarzschild BH. When the spacetime deformation is set as $ n = 1 $, the peak intensity for the new regular BHs corresponding to $ \alpha_0 = 0.72 $ (represented by the green dashed line) is greater than that of the case with $ \alpha_0 = 0.2 $ (represented by the green solid line). Similarly, for the spacetime deformation factors $ n = 2 $ and $ n = 3 $, the peak intensity corresponding to $ \alpha_0 = 0.72 $ (represented by the blue and red dashed lines) is also greater than that for $ \alpha_0 = 0.2 $ (represented by the blue and red solid lines). These results imply that the larger the value of $ \alpha_0 $, the stronger the observed specific intensity of the new regular BHs. Notably, the parameter $ \alpha_0 $ arises from the corrections due to the quantum gravity effect, indicating that the stronger the quantum gravity effect, the higher the luminosity of the new regular BHs.

Furthermore, Fig. 3 shows that, for the parameter $ \alpha_0 = 0.72 $, the peak intensity decreases in the order of $ n = 1 $, $ n = 2 $, and $ n = 3 $, corresponding to the green dashed, blue dashed, and red dashed lines, respectively. Similarly, for the parameter $ \alpha_0 = 0.2 $, the peak intensity also decreases sequentially for $ n = 1 $, $ n = 2 $, and $ n = 3 $, corresponding to the green solid, blue solid, and red solid lines, respectively. This implies that as the parameter n increases, the observed specific intensity of the new regular BHs gradually weakens, indicating that a smaller value of n can increase the optical brightness and enable the observer to detect more luminous signals.

Finally, in Fig. 3, $ \Delta I $ represents the difference in peak intensities for $ n = 1 $ and $ n = 2 $ corresponding to $ \alpha_0 = 0.72 $, whereas$ \Delta I' $ represents the difference for $ n = 1 $ and $ n = 2 $ corresponding to $ \alpha_0 = 0.2 $. It is evident that $ \Delta I $ is greater than $ \Delta I' $, which means that the difference between peak intensities becomes more pronounced as the parameter $ \alpha_0 $increases. This in turn indicates that, the larger the value of $ \alpha_0 $, the easier it is to distinguish between these new regular BHs for different values of n through the observed specific intensity. We set $ n = 1 $ and $ n = 2 $ as examples and present the two-dimensional image of the observed specific intensity for the new regular BHs for different values of $ \alpha_0 $ in Fig. 4.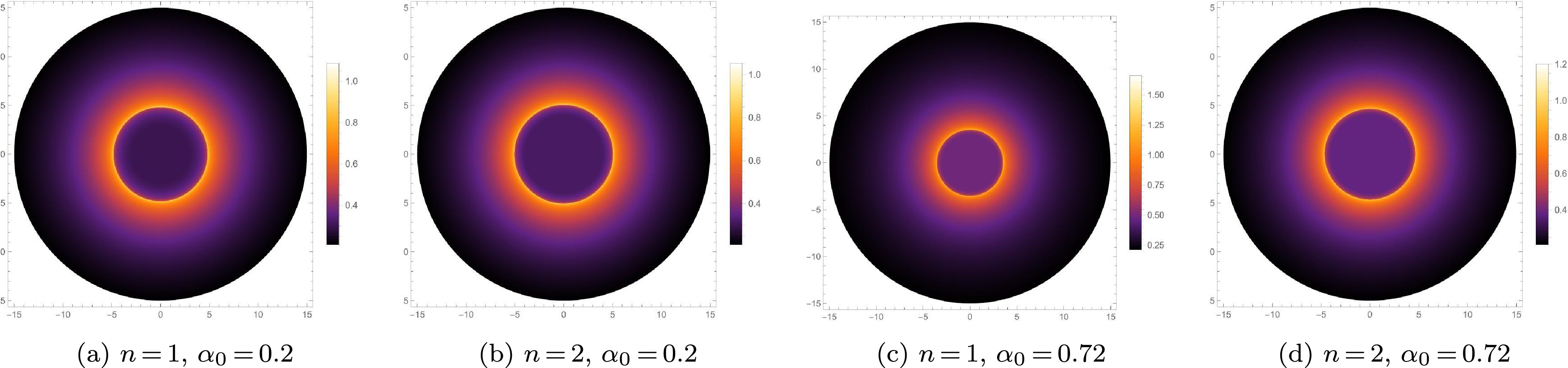

Figure 4.  (color online) Optical appearances of the new regular BHs under static spherical accretion for different values of $ \alpha_0 $ and n.

In Fig. 4, the photon sphere corresponds to the bright ring with the highest luminosity. It can be observed that the region inside the photon sphere is not completely dark, as a small fraction of radiation can escape from the new regular BHs, resulting in weak luminosity near the photon sphere. Evidently, the parameters $ \alpha_0 $ and n have a significant impact both on the photon ring brightness and shadow radius. In Fig. 4, we can see that, for a given n, a larger value of $ \alpha_0 $ leads to a brighter photon ring of the BH image but a smaller radius of the BH shadow and photon sphere. For a given $ \alpha_0 $, a larger value of n leads to a dimmer photon ring of the BH image but a larger radius of the BH shadow and photon sphere.

In addition, as $ \alpha_0 $ increases, the differences between the shadow images for $ n = 1 $ and $ n = 2 $ become more apparent in Fig. 4. Therefore, under the static spherical accretion model, the enhancement of the quantum gravity effect can increase the luminosity of the photon ring and enlarge the shadow radius for the new regular BHs. As n decreases, the enhancement of the quantum gravity effect becomes more pronounced. This is because a smaller value of n amplifies the influence of $ \alpha_0 $ on the optical characteristics of the new regular BHs, thereby making it easier for the observer to distinguish these new regular BHs.

In this section, we investigate the shadow images of the new regular BHs with a Minkowski core surrounded by infalling spherical accretion. This is a dynamical model in which the accretion is assumed to move radially toward the BH. In this case, the observed specific intensity described by Eq. (15) remains applicable, but the corresponding redshift factor differs from that in static spherical accretion. The redshift factor for infalling spherical accretion can be expressed as

Here,$ \quad {K}^{\mu} $ represents the four-momentum of a photon emitted by the accreting matter, $ u_{0}^{\rho} = (1, 0, 0, 0) $ corresponds to the four-velocity of a static observer, and $ u_{e}^{\sigma} $ denotes the four-velocity of the infalling accretion, given by

The four-momentum of the photon is derived from the null geodesic, which is expressed as

Note that, in $ K_{r} $, the $ + $ or $ - $ sign indicates whether the photon is moving radially inward or outward from the BH. For the case of the infalling spherical accretion, the redshift factor can be written as

Furthermore, unlike the static spherical accretion case, the proper distance $ {\rm d} l_{\text{prop}} $ is defined as the spatial distance measured in the local rest frame of the infalling spherical accretion. The four-momentum $K^\mu = {\rm d}x^\mu/{\rm d}\lambda$ (with $ K^\mu K_\mu = 0 $) is projected onto the spatial hypersurface orthogonal to $ u_e^\mu $ using the projection tensor $ h_\nu^\mu = \delta_\nu^\mu + u_e^\mu u_{e\nu} $; therefore, we have

In the local rest frame, the magnitude of the spatial momentum $ \vert K_{\perp}^\mu \vert $ is given by

Given that $ K^\mu $ and $ u_e^\mu $ denote null and infalling accretions, respectively, their inner product is $ K_\mu u_e^\mu < 0 $. Hence, $ \vert K_{\perp}^\mu \vert = -K_\mu u_e^\mu $. The proper distance $ {\rm d} l_{\text{prop}} $ traveled by the photon in the local rest frame over an affine parameter interval $ {\rm d}\lambda $ is

By convention, the negative sign is absorbed into the definition, yielding

The observed specific intensity for the infalling spherical accretion is calculated as

Based on this equation, we can obtain the variation of the observed specific intensity $ I_{\text{obs}} $ with the impact parameter b for different values of the parameters $ \alpha_0 $ and n, observed by an observer at infinity.

We selected the cases of $ \alpha_0 = 0.2 $ and $ \alpha_0 = 0.72 $ as well as $ n = 1 $ and $ n = 2 $ for representation in Fig. 5. Note that, as the impact parameter b increases, the observed specific intensity increases slowly. When the impact parameter b approaches the critical value $ b_c $, the observed specific intensity increases rapidly and reaches a peak. Subsequently, as b continues to increase, the observed specific intensity gradually decreases. The variation of the observed specific intensity is closely related to the parameters n and $ \alpha_0 $. For a fixed n and increase in $ \alpha_0 $, the impact parameter b corresponding to the peak position of the observed specific intensity decreases, and the peak intensity increases. For a fixed $ \alpha_0 $and increase in n, the impact parameter b corresponding to the peak position of the observed specific intensity increases, and the peak intensity decreases.

Figure 5.  (color online) Variation of the observed specific intensity radiated from the infalling spherical accretion with the impact parameter for different values of $ \alpha_0 $ and n. We set $ M = 1 $.

Figure 6 shows the optical appearances of the new regular BHs under infalling spherical accretion. By comparing Figs. 6(a) and 6(c), it can be concluded that, as $ \alpha_0 $ increases, the peak intensity becomes higher, while the shadow and photon sphere radii become smaller. Conversely, by comparing Figs. 6(c) and 6(d), it can be concluded that, as the parameter n increases, the peak intensity becomes smaller, and the shadow and photon sphere radii become larger. Moreover, by comparing the differences in the photon ring and shadow radius between Figs. 6(a) and 6(c), as well as between Figs. 6(b) and 6(d), it can be concluded that, as $ \alpha_0 $ increases, the differences in the optical appearances of $ n = 1 $ and $ n = 2 $ become more evident. Therefore, under infalling spherical accretion, the larger the value of $ \alpha_0 $, the greater the luminosity of the photon ring but the smaller the shadow radius. Conversely, as the parameter n increases, the photon ring becomes dimmer, and the shadow radius becomes larger.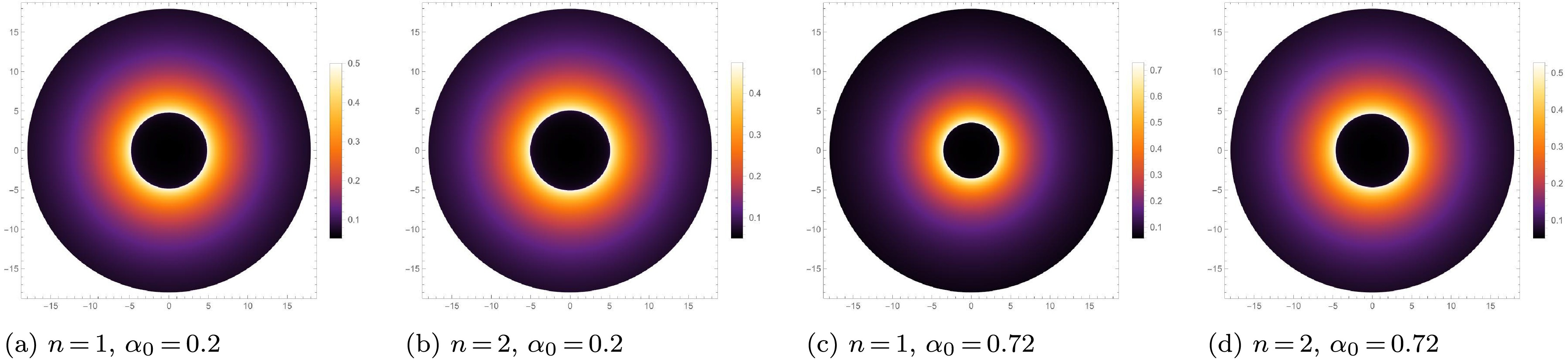

Figure 6.  (color online) Optical appearances of the new regular BHs under infalling spherical accretion for different values of $ \alpha_0 $ and n.

Combining the results in Fig. 4 under static spherical accretion and those in Fig. 6 under infalling spherical accretion, for an observer at infinity, the observed specific intensity, shadow radius, and photon sphere radius of the new regular BHs with a Minkowski core are closely related to the intrinsic parameters of the BHs themselves. Under both spherical accretions, the larger the value of$ \alpha_0 $, the larger the observed specific intensity, while the shadow and photon sphere radii decrease. In contrast, as n increases, the observed specific intensity decreases, while the shadow and photon sphere radii increase. By comparing the results of the two spherical accretion models, we found that the shadow radius and location of the photon sphere are independent of the choice of spherical accretion model. However, the observed specific intensity of the new regular BHs depends on the choice of spherical accretion model: the specific intensity from static spherical accretion is significantly higher than that from infalling spherical accretion. This indicates that the BH shadow reflects the intrinsic properties of the BH spacetime, while the choice of accretion model only influences the observed specific intensity and not the structure of the BH shadow itself. Therefore, the spacetime characteristics of the new regular BHs can be distinguished by observing and analyzing their shadows.

In the next section, we further compare the shadows formed by these new regular BHs with a Minkowski core and traditional regular BHs with a dS core under the two different spherical accretion models. We also discuss the application of shadow analysis in distinguishing regular BHs with different cores.

As previously mentioned, the new regular BHs exhibit an asymptotic behavior similar to that of traditional Bardeen/Hayward BHs on large scales, but they differ in terms of the central region. Specifically, the new regular BHs have a Minkowski core, while the traditional Bardeen/Hayward BHs possess a dS core. It has been found that, under the thin accretion disk model reported in [17], the optical observational characteristics of the new regular BHs and the corresponding traditional Bardeen BHs may differ. Based on this, in this section, we further compare the shadows and optical appearances of the new regular BHs with those of the corresponding traditional Bardeen/Hayward BHs under the spherical accretion model. Additionally, as shown in the previous section, different spherical accretion models can affect the observed specific intensities of the shadows. Therefore, we also compare the shadows of the new regular BHs and the corresponding traditional regular BHs under both static and infalling spherical accretion models.

According to the previous discussion, when $ n = 2 $ and $ x = 2/3 $ and when $ n = 3 $ and $ x = 1 $, the new regular BHs show a one-to-one correspondence with the Bardeen and Hayward BHs, respectively, on a large scale. Note that the cores of these new regular BHs are different from those of traditional regular BHs at the center. To compare the shadows of regular BHs with different cores, Figs. 7 and 8 present the observed specific intensity and optical appearances of both types of regular BHs with different cores under static accretion.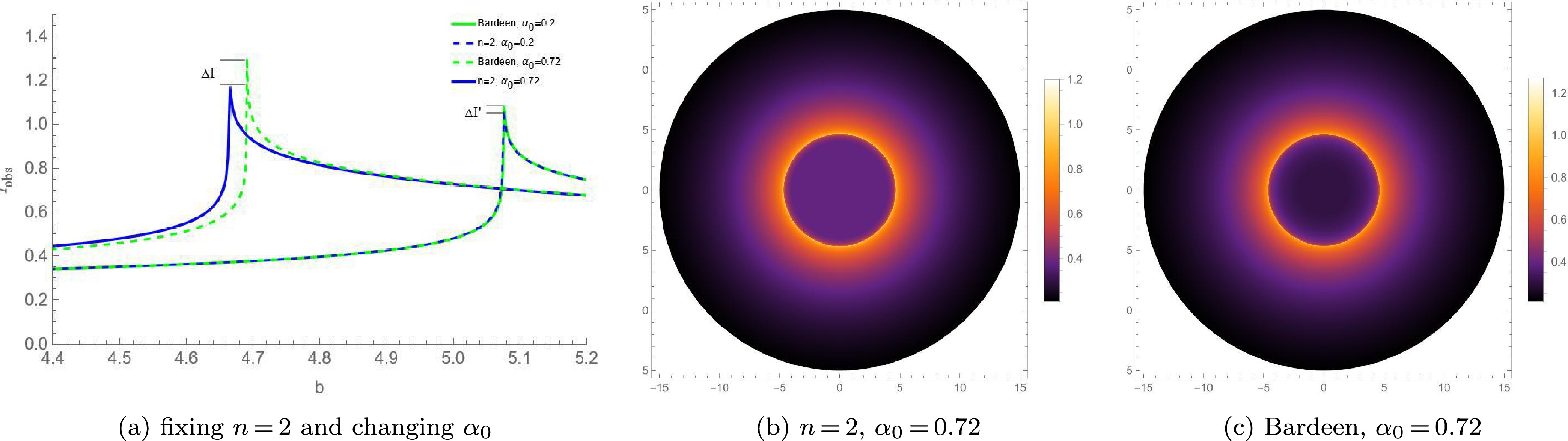

Figure 7.  (color online) Observed specific intensity and optical appearances under static spherical accretion for the new regular BH with $ n = 2 $ and corresponding Bardeen BH.

Figure 8.  (color online) Observed specific intensity and optical appearances under static spherical accretion for the new regular BH with $ n = 3 $ and corresponding Hayward BH.

First, it can be observed from Figs. 7(a) and 8(a) that the peak intensity of the new regular BHs with a Minkowski core is always smaller than that of traditional regular BHs with a dS core. Here, $ \Delta I $ and $ \Delta I' $ represent the differences in the peak intensities of the regular BHs with different cores for the same $ \alpha_0 $, with $ \Delta I > \Delta I' $. This implies that, the larger the value of $ \alpha_0 $, the greater the difference in the peak intensities of these BHs with different cores, and the higher the significance of the corresponding difference in total observed intensity.

Secondly, Figs. 7(b), 7(c), 8(b), and 8(c) present the optical appearances of these BHs with different cores when $ \alpha_0 = 0.72 $ and $ \alpha_0 = 0.92 $, respectively. It is evident that the photon ring of these regular BHs with a Minkowski core is significantly dimmer than that of the traditional regular BHs with a dS core. Moreover, the shadow and photon sphere radii of the former are also smaller than those of the latter. This indicates that, under the static spherical accretion model, compared with traditional regular BHs, the new regular BHs have a dimmer photon ring, and both types exhibit different optical observational characteristics; as $ \alpha_0 $ increases, the differences in the optical observational features between regular BHs with different cores become more significant, making it easier to distinguish them from their optical features.

Finally, by comparing Figs. 7 and 8, it can be concluded that, under static spherical accretion, the difference between the Bardeen and new regular BHs corresponding to $ n = 2 $ is more evident than that between the Hayward and new regular BHs corresponding to $ n = 3 $. This once again proves that, the smaller the value of n, the easier it is for observers to distinguish these regular BHs with different cores.

Under the infalling spherical accretion model, the observed specific intensity and optical appearances of the new regular BHs with $ n = 2 $ and $ n = 3 $, along with their corresponding Bardeen/Hayward BHs, are shown in Figs. 9 and 10, respectively. It can be observed that there are only slight differences in the shadows between the regular BHs with a Minkowski core and the traditional regular BHs with a dS core. As $ \alpha_0 $ increases, the shadow and photon sphere radii of the former are slightly smaller than those of the latter, and the photon ring of the former is slightly dimmer than that of the latter. This difference becomes slightly more evident only when $ \alpha_0 $ is relatively large.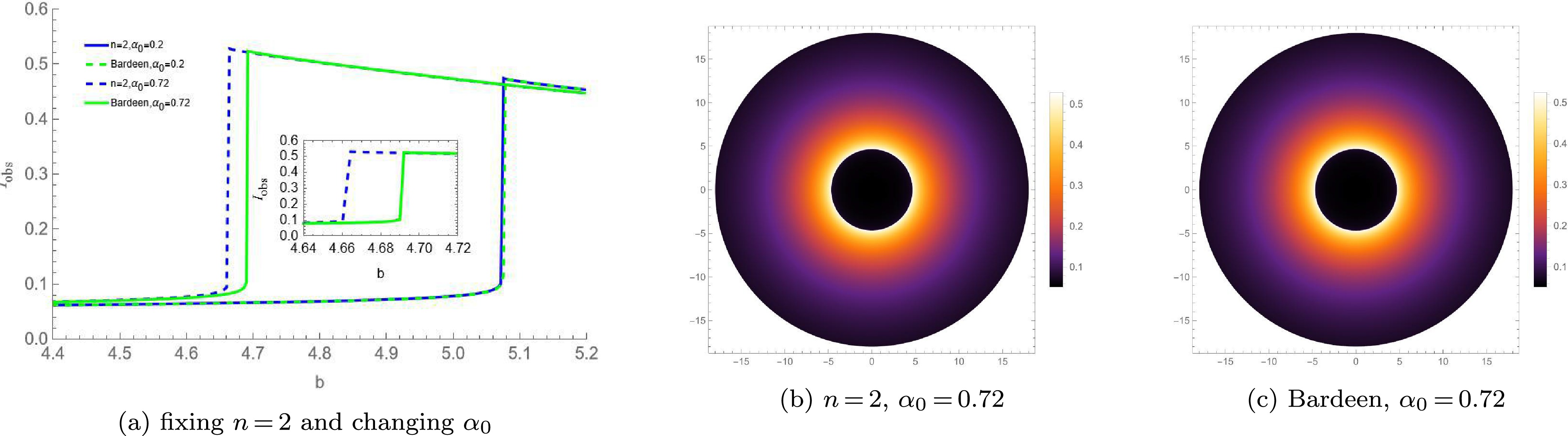

Figure 9.  (color online) Observed specific intensity and optical appearances under infalling spherical accretion for the new regular BH with $ n = 2 $ and corresponding Bardeen BH.

Figure 10.  (color online) Observed specific intensity and optical appearances under infalling spherical accretion for the new regular BH with $ n = 3 $ and corresponding Hayward BH.

The shadows of the new regular BHs with a Minkowski core and those of the corresponding traditional regular BHs with a dS core (Bardeen/Hayward BHs) were comparatively analyzed under two spherical accretion models. The shadows of the new regular BHs differ from those of the traditional regular BHs. Specifically, the new regular BHs exhibit a lower peak intensity, a dimmer photon ring, and smaller shadow and photon sphere radii. Moreover, as $ \alpha_0 $ increases, these differences become more pronounced, making it easier to distinguish regular BHs with different cores through their optical observational characteristics. Additionally, the differences are more significant under the static spherical accretion model.

In this study, we explored the shadows of new regular BHs with a Minkowski core under different spherical accretion models and compared them with traditional regular BHs with a de Sitter (dS) core (Bardeen/Hayward BHs). The results reveal that, under both static and infalling spherical accretion, the observed specific intensity, shadow radius, and photon sphere radius of these new regular BHs are closely linked to their intrinsic parameters. As the quantum gravity parameter $ \alpha_0 $increases, the observed specific intensity increases, and the shadow and photon sphere radii decrease. Conversely, as the spacetime deformation parameter n increases, the observed specific intensity decreases, and the shadow and photon sphere radii increase. Moreover, the shadow and photon sphere radii are unaffected by the choice of spherical accretion model, whereas the observed specific intensity varies between models, being higher in static spherical accretion than in infalling spherical accretion.

Secondly, there are differences in the shadows of the two types of regular BHs with different cores, and these differences are more pronounced in static spherical accretion. Taking a new regular BH with a Minkowski core ($ n = 2 $, $ x = 2/3 $) and a Bardeen BH as an example, the former has a smaller observed specific intensity, a dimmer photon ring, and smaller shadow and photon sphere radii. More importantly, these differences become more significant as $ \alpha_0 $ increases. Similarly, the new regular BHs ($ n = 3 $ and $ x = 1 $) and Hayward BHs exhibit a similar trend. In the infalling sphere accretion, there are only subtle differences in observed specific intensity, and the differences are only slightly more evident when $ \alpha_0 $ is relatively large.

Additionally, the results show that the shadows reflect the intrinsic properties of the BH spacetime, and the choice of spherical accretion model only affects the observed specific intensity of the shadows and not the structure of the BH shadow itself. Therefore, the spacetime characteristics of these new regular BHs can be distinguished by observing and analyzing their shadows.

In this study, we only applied two models: static spherical accretion and infalling spherical accretion. In fact, more complex accretion models can be studied, such as those incorporating the effects of magnetic fields or non-spherical accretion. It will help us to more comprehensively understand the changes in the shadows of BHs under different accretion scenarios and provide a more abundant theoretical foundation for astronomical observations. Meanwhile, our focus in this study was on comparing these new regular BHs with a Minkowski core to traditional regular BHs with a de Sitter core. Future research could expand the parameter ranges to study BH shadows under a wider variety of parameter combinations. With ongoing advances in astronomical observation technology, the accuracy and scope of observational data continue to improve. Strengthening the integration of theoretical research with experimental observations is crucial. High resolution BH images and other observational data can be used to more precisely test theoretical models. By comparing theoretical shadow calculations with observational results, models can be continuously refined, enhancing our understanding of BH properties. Furthermore, studying the correlations between BH shadows and other astrophysical phenomena, such as BH spin and the distribution and dynamics of matter around BHs, is important. Exploring how these factors jointly influence the observational characteristics of shadows will contribute to a more comprehensive understanding of the physical processes around BHs and their role in galaxy evolution.