Impact of particle production mechanisms on pseudorapidity distribution and directed flow in Au+Au and Cu+Cu collisions at ${ \sqrt{{\boldsymbol s}_{\boldsymbol{ NN}}}}$ = 19.6 GeV using AMPT model

Relativistic heavy-ion collisions allow studying the behavior of a strongly interacting matter comprising quarks and gluons called Quark Gluon Plasma (QGP), which is governed by Quantum Chromodynamics (QCD). Heavy-ion collision experiments at facilities such as the RHIC and LHC [3−8] have established the existence of a strongly coupled QGP. Measurement of collective flow, described by the Fourier coefficients of the azimuthal angle of the produced particles, has been widely used to study the properties and dynamics of the QGP [9−11]. The first Fourier coefficient of anisotropic flow, called directed flow ($ v_{1} $) [12], is of special interest because it is sensitive to the early time dynamics and equation of state (EoS) of the systems. Typically, the $ v_{1} $ value of produced particles is measured according to the following expression:

where ϕ is the azimuthal angle, and $ \Psi_{RP} $ is the reaction plane determined by the impact parameter and beam-axis. The average, denoted by $ \langle ... \rangle $, is performed over all particles and all events. Primarily, we focused on the rapidity-odd component of directed flow in this study. Extensive research on $ v_{1} $ of several identified particles has been conducted at AGS [13, 14], SPS [15], RHIC [16, 17], and LHC [18] energies. A key research topic has been to search for a change in the sign of proton and net-proton $ v_{1} $, owing to its potential connection with the softening of the EoS associated with the QCD phase transition [19−21]. The STAR experiment has observed a sign change in proton $ v_1 $ and a double sign change in net-proton $ v_1 $ near $ \sqrt{s_{NN}} = 10 $–$ 20 $ GeV [22, 23]. However, to date, no model has been able to accurately capture this pattern or the position of the sign change, making $ v_1 $ one of the most challenging observables to model [24].

Furthermore, the rapidity-odd $ v_{1} $ is also sensitive to electromagnetic field effects in heavy-ion collisions [25, 26]. It is usually probed via differences in $ v_{1} $ for particles and anti-particles (called $ \Delta v_1 $) [27, 28]. Recent high-statistics data from the STAR experiment revealed intriguing features in $ \Delta v_1 $ for light-quark hadrons. At top RHIC energy, $ \Delta v_1 $ is positive in (mid-)central collisions for protons and kaons. However, it becomes significantly negative in peripheral collisions. The positive values are attributed to transported quarks, while the negative values are consistent with electromagnetic effects dominated by Faraday induction [29]. Additionally, $ \Delta v_1 $ was found to increase with both electric charge and strangeness differences in mid-central collisions [30]. More recently, STAR reported simultaneous measurements of $ v_1 $ and $ \Delta v_1 $ for π, K, and p in $\rm U+U $, $\rm Au+Au $, and isobar ($\rm Ru+Ru $, $\rm Zr+Zr $) collisions [2]. A clear system-size dependence of $ v_1 $ and $ \Delta v_1 $ has been observed for protons and antiprotons, with ordering $ \Delta v_1 $: $\rm U+U > Au+Au > $ ($\rm Ru+Ru $, $\rm Zr+Zr $), especially in central and mid-central collisions; mesons do not exhibit such dependence. This apparently contrasts with earlier RHIC results for inclusive charged particles, where $ v_1 $appears to be system-size independent. A relativistic dissipative hydrodynamic model including baryon diffusion [31, 32] qualitatively reproduces the observed $ \Delta v_1 $ trends for baryons as well as their system-size dependence. However, it fails to simultaneously describe the $ \Delta v_1 $ sign and centrality trends across $ \pi^{\pm} $, $ K^{\pm} $, and $ p (\bar{p}) $ [33]. At lower energies, mean-field potentials may significantly influence $ v_1 $ and its charge dependence [34−36], though these effects were not considered in the present study.

In this study, we investigated the directed flow ($ v_1 $) and its system-size dependence for π, K, and p at lower beam energies, where the magnitude of $ v_1 $ is significantly larger, thereby facilitating its analysis. For this purpose, we used Au+Au and Cu+Cu collisions at $ \sqrt{s_{NN}} = $ 19.6 GeV within A Multi-Phase Transport (AMPT) model framework [37]. To gain insights into the connection between the particle production mechanisms near mid-rapidity and their influence on the directed flow, we also analyzed the pseudorapidity distributions of π, K, and p, along with their charge-dependent differences.

In this study, we used the default version of the AMPT model [37], which is a hybrid transport model consisting of four major components: (i) the initial conditions are obtained from HIJING [38]; minijets coexist with the remnants of their originating nucleons, collectively forming newly excited strings; (ii) the scattering among partons is modeled by Zhang's Parton Cascade (ZPC) [39]; (iii) when the minijet partons stop interacting, they are combined with their parent strings to form excited strings, which are then converted to hadrons according to the Lund string fragmentation model [40−42]; (iv) and finally, the evolution of hadronic matter is described by a hadron cascade built upon A Relativistic Transport (ART) framework [43]. The ART framework accounts for both elastic and inelastic scatterings involving baryon-baryon, baryon-meson, and meson-meson interactions.

In the string fragmentation model, mesons are conceptualized as having a short string connecting their quark and antiquark endpoints, whereas baryons are described as three-quark structures. The PYTHIA/JETSET subroutines within the AMPT model incorporate particle production based on the Lund string fragmentation model [37, 42]. The probability of a string splitting into hadrons is governed by the Lund symmetric fragmentation function:

where z corresponds to the fraction of the energy-momentum of the string taken by one fragment; $ m_{T} = \sqrt(m^2 + p_{T}^{2}) $ is the transverse mass of the produced hadrons; a and b are parameters controlling the shape of the splitting function; and m is the mass of the produced hadron. The parameters a and b in the Lund fragmentation function are approximately related to the string tension (κ) as

The values of the a and b parameters can be controlled by the $\mathrm{PARJ(41)} $ and $\mathrm{PARJ(42)} $ parameters in AMPT. In this study, these parameters were determined by fitting the charged particle yield and $ p_{T} $ spectra in different collision systems. Note that a larger value of a corresponds to a softer fragmentation function, leading to a smaller average transverse momentum for produced hadrons, thereby increasing the particle multiplicity. The default values used in AMPT are $ a=0.55 $ and $ b=0.15 $ GeV$ ^{-2} $. We changed these values to $ a=2.2 $ and $ b=0.15 $ GeV$ ^{-2} $ to check their impact on $ {\rm d}N/{\rm d}y $ and especially on $ v_{1} $ of identified particles.

Furthermore, in the string breaking picture, a straightforward approach involves the diquark model, where quarks are treated as either individual quarks or antidiquarks in a color triplet state. In this framework, baryons and antibaryons are formed as neighboring entities along the string. An alternative mechanism, referred to as the “popcorn mechanism,” allows for baryon production without direct diquark formation. Instead, baryons emerge through the sequential production of quark-antiquark pairs facilitated by fluctuations in the color field. The basic version of this mechanism permits at most one intermediate meson to form during the process (e.g., a $ q\bar{q} $ string breaking into a $ BM\bar{B} $ structure). An extended version of this mechanism, however, allows for the creation of multiple mesons during the string breaking process (e.g., a $ q\bar{q} $ string breaking into a $ BMM\bar{B} $ structure), as detailed in related studies. These string breaking processes can significantly influence meson and baryon production near mid-rapidity; they have been studied using the AMPT model [44]. The stopping of baryons and their transport to mid-rapidity is a key phenomenon extensively studied in high-energy nuclear collisions. This process is closely related to the total energy deposited in the system. The observation of an increase in stopped baryons near mid-rapidity has led to the proposal of novel mechanisms, such as the gluon junction mechanism. In the AMPT model, baryon stopping is phenomenologically incorporated via the popcorn mechanism. The parameter $ \mathrm{MSTJ(12)}$ governs the operation of the popcorn mechanism. When $\mathrm{MSTJ(12) = 0} $, the string breaks directly into a baryon-antibaryon pair without the production of intermediate mesons. Meanwhile, values of $ \mathrm{MSTJ(12) > 0}$ enable the creation of intermediate mesons. Another parameter, $\mathrm{PARJ(5)} $, determines the probability of meson production between baryon-antibaryon pairs when the popcorn mechanism is active. In PYTHIA, the $ \mathrm{PARJ(5)}$ parameter is related to baryon and meson production via the following relation:

This parameter controls the relative percentage of $ B\bar{B} $ and $ BM\bar{B} $ channels. We studied the impact of $\mathrm{MSTJ(12)} $ and $\mathrm{PARJ(5)} $ on the $ {\rm d}N/{\rm d}y $ and $ v_{1} $ values of identified particles.

We performed AMPT simulations comprising approximately one million events for each of the previously mentioned configurations, as presented in Table 1, covering an impact parameter ranging from 0.0 to 15.0 fm. Figures 1 and 2 show the pseudorapidity distribution ($ {\rm d}N/{\rm d}y $) for $ \pi^{+} $, $ K^{+} $, and p and their antiparticles, respectively, in Au+Au and Cu+Cu collisions at $ \sqrt{s_{NN}} $ = 19.6 GeV for three different collision centralities, with and without the popcorn mechanism. Enabling the popcorn mechanism in AMPT with $ \mathrm{PARJ(5)}$=1 increases the yields for $ \pi^{+} $ ($ \pi^{-} $) and p near mid-rapidity while decreasing the $ K^{\pm} $ and $ \bar{p} $ yields. A similar feature is observed for both Au+Au and Cu+Cu collisions. For the net particle pseudorapidity distribution (denoted as $ \Delta {\rm d}N/{\rm d}y $; see Fig. 3), defined as the difference between particle and antiparticle yields, the popcorn mechanism increases the mid-rapidity yield for kaons and protons, while for pions, the relative change is small. In a previous AMPT-based study, it was observed that setting equal probabilities for the $ B\bar{B} $ and $ BM\bar{B} $ configurations allows the reproduction of the net-baryon rapidity distribution at SPS energies. It was also observed that, without the popcorn mechanism, as implemented by default in the HIJING model, the net-baryon rapidity distribution would peak at a larger rapidity. Figure 4 presents the $ {\rm d}N/{\rm d}y $ distribution for two different implementations of the Lund string parameter a with the popcorn mechanism: a = 0.55 and a = 2.2. As expected, larger values of a increase the mid-rapidity yields for all species (π, K, and p). By varying the Lund string fragmentation mechanism, we altered the mid-rapidity yields of particles. Next, we studied the impact of these changes on the directed flow. As discussed in [37], the default values of the a and b parameters in HIJING can reproduce charged particle multiplicities in elementary collisions. Consequently, these parameters in the AMPT model may better describe peripheral collisions compared to central collisions. Although the a and b values in the AMPT model can be varied with centrality to better explain the data, we have not yet investigated the extent of this variation. We compared our calculations of mid-rapidity in terms of $ {\rm d}N/{\rm d}y $ and $ \Delta {\rm d}N/{\rm d}y $ with STAR data ($ |y|<0.1 $) for Au+Au collisions [45] and observed that the results from the 40%–80% centrality bins are comparable with AMPT, whereas AMPT underpredicts the values for mid-central and central collisions.

Parameters	$\mathrm{MSTJ(12)} $	$\mathrm{PARJ(5)} $	$\mathrm{PARJ(41)} $	$\mathrm{PARJ(42)} $
set-1: no-popcorn	0	0	0.55	0.15
set-2: popcorn	1	0.5	0.55	0.15
set-3: popcorn	1	1	0.55	0.15
set-4: popcorn	1	1	2.2	0.15

Table 1.  Lund string fragmentation parameters used in AMPT simulation.

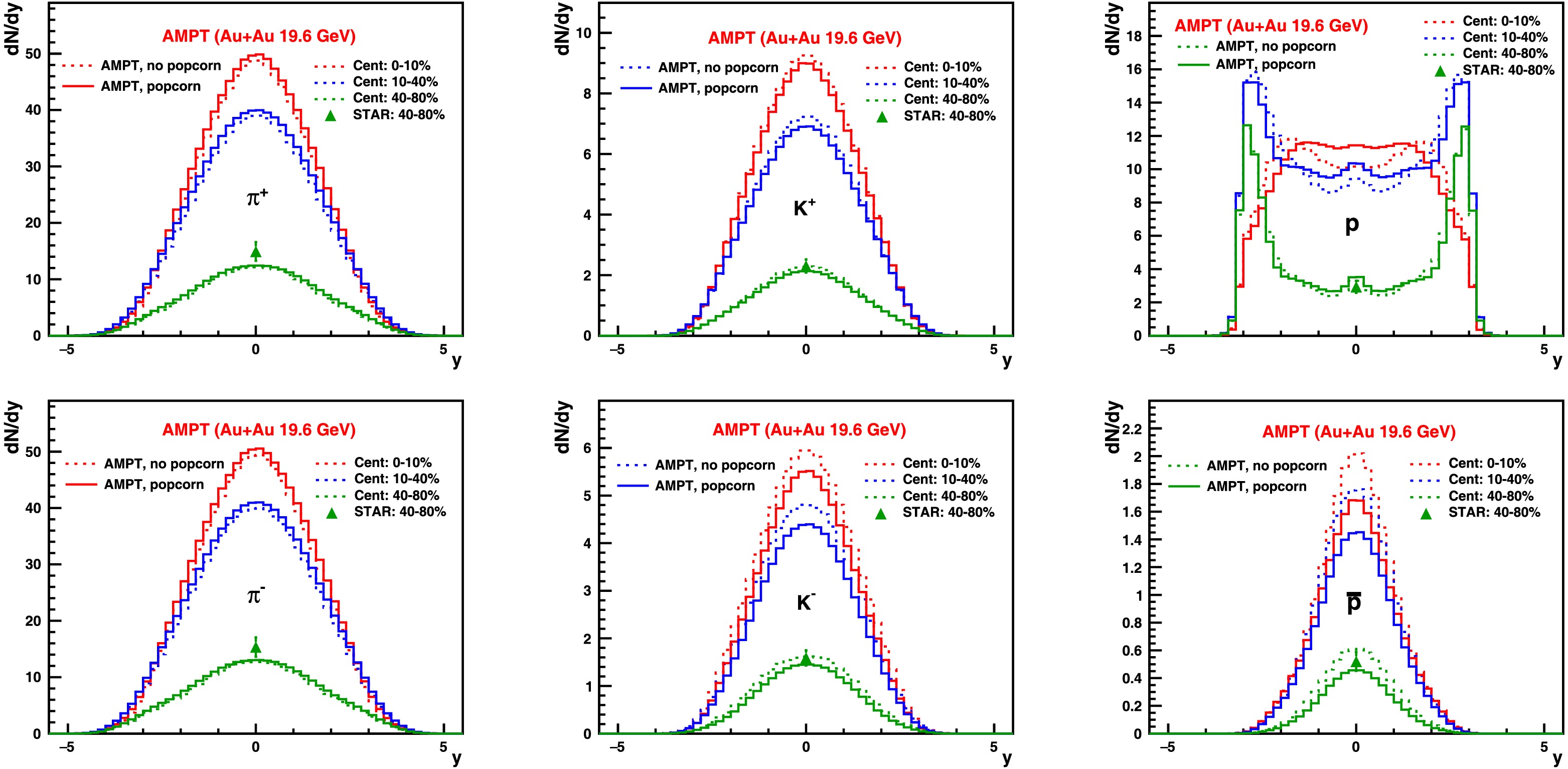
Figure 1.  (color online) Pseudorapidity (${\rm d}N/{\rm d}y$) distribution for π, $K$, and $p$ and their antiparticles in Au+Au collisions at $\sqrt{s_{NN}}$ = 19.6 GeV for different collision centralities with and without the popcorn mechanism (Table 1: set-1 and set-3) using the AMPT model. The STAR data points ($|y|<0.1$) are taken from [45].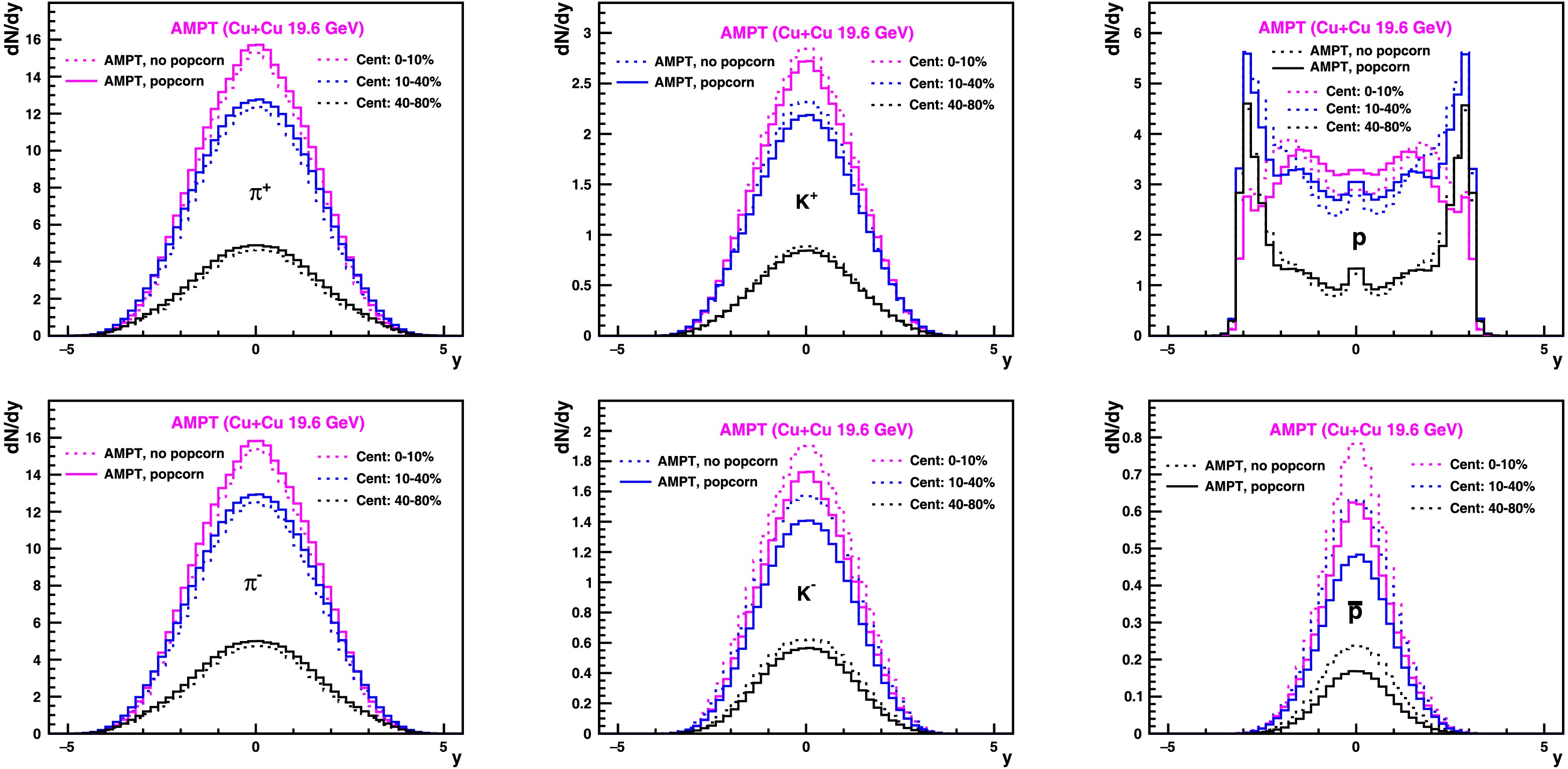

Figure 2.  (color online) Pseudorapidity (${\rm d}N/{\rm d}y$) distribution for π, $K$, and $p$ and their antiparticles in Cu+Cu collisions at $\sqrt{s_{NN}}$ = 19.6 GeV for different collision centralities with and without the popcorn mechanism (Table 1: set-1 and set-3) using the AMPT model.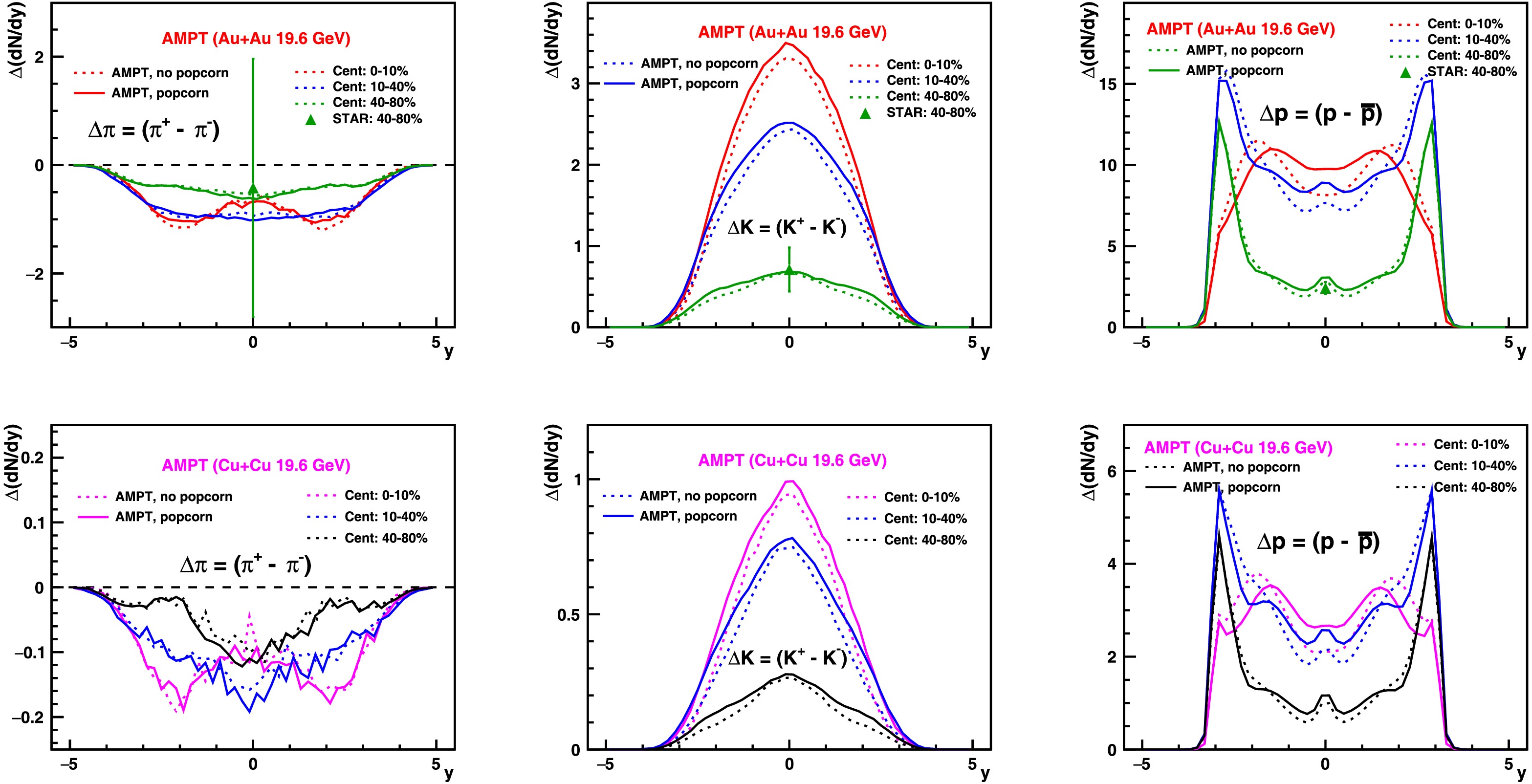

Figure 3.  (color online) Pseudorapidity (${\rm d}N/{\rm d}y$) distribution for net-π, net-$K$, and net-$p$ in Au+Au and Cu+Cu collisions at $\sqrt{s_{NN}}$ = 19.6 GeV for different collision centralities with and without the popcorn mechanism (Table 1: set-1 and set-3) using the AMPT model. The STAR data points ($|y|<0.1$) are taken from [45].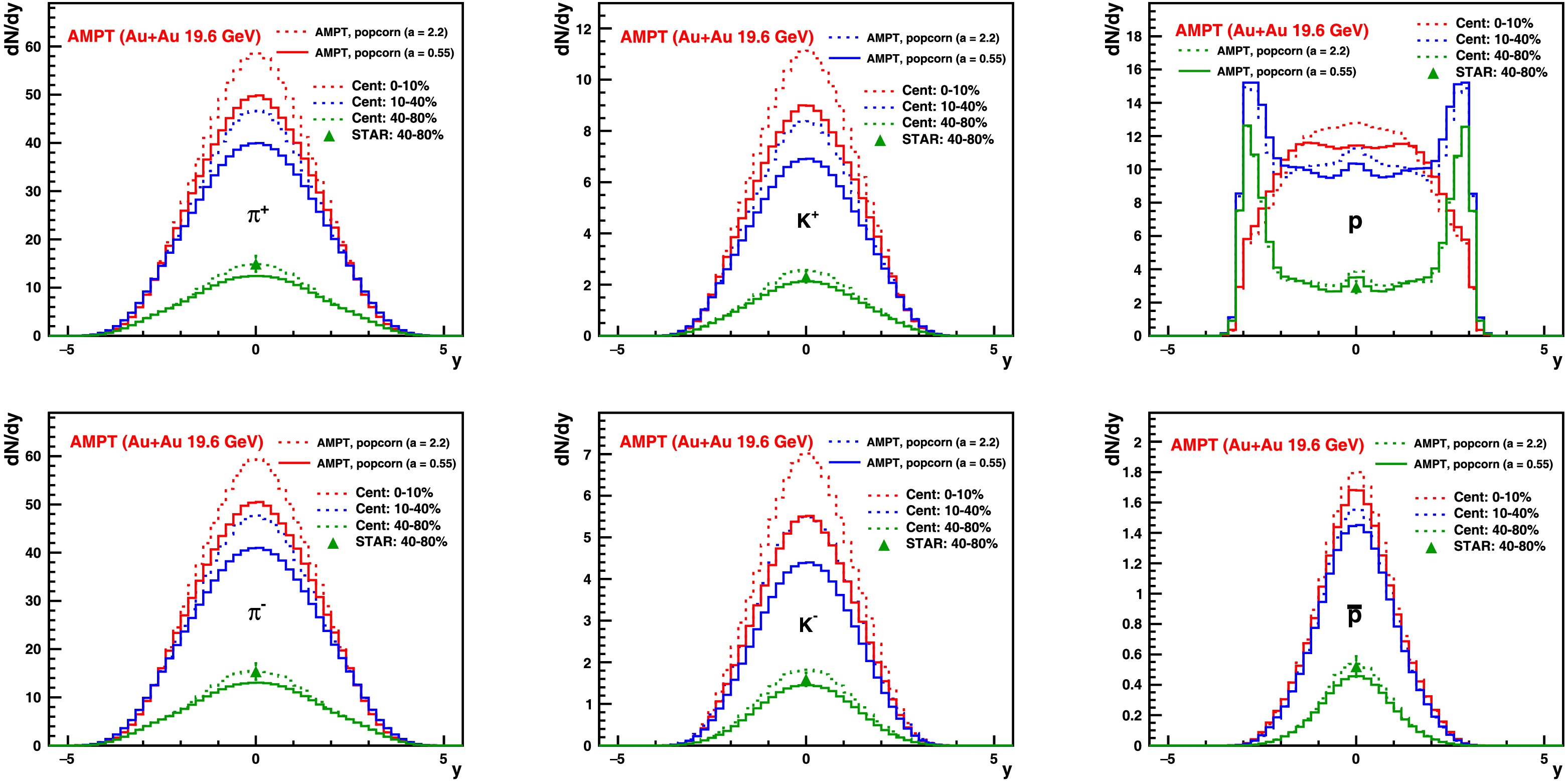

Figure 4.  (color online) Pseudorapidity (${\rm d}N/{\rm d}y$) distribution for π, $K$, and $p$ in Au+Au collisions at $\sqrt{s_{NN}}$= 19.6 GeV for different collision centralities, two cases of the popcorn mechanism, and Lund fragmentation parameter values a=0.55 and a=2.2 (Table 1: set-3 and set-4), using the AMPT model. The STAR data points ($|y|<0.1$) are taken from [45].

The top and bottom panels in Fig. 5 presents the rapidity dependence of $ v_{1} $ for $ \pi^{+} $, $ K^{+} $, p, and their antiparticles for mid-central (10%−40%) Au+Au and Cu+Cu collisions respectively at $ \sqrt{s_{{NN}}} = 19.6 $ GeV using popcorn process in AMPT. The values of$ v_{1} (y) $ were fitted with a linear function within $ -1.0 < y < 1.0 $ to extract the slope near mid-rapidity or $ {\rm d}v_{1}/{\rm d}y $. The values of $ {\rm d}v_{1}/{\rm d}y $ were studied as a function of centrality and also for ultra-central collisions ($ b<1 $ fm/c).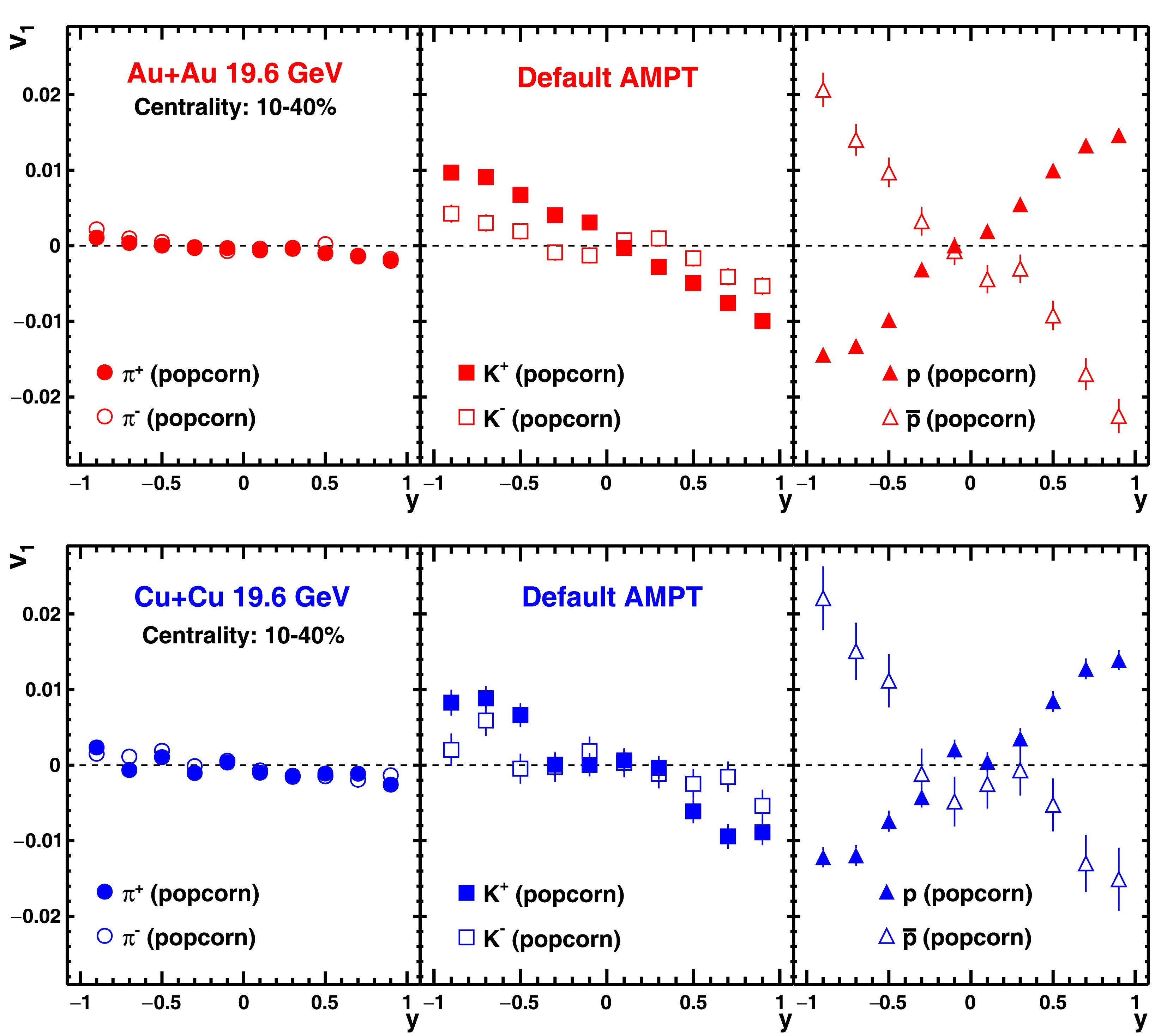

Figure 5.  (color online) Directed flow $v_{1} (y)$ for $\pi^{+}$, $K^{+}$, $p$, and their antiparticles in Au+Au and Cu+Cu collisions at $\sqrt{s_{NN}}$= 19.6 GeV for 10%–40% centrality with the popcorn mechanism and Lund fragmentation parameter values a=0.55 and b=0.15 GeV$^{2}$ (Table 1: set-3), using the AMPT model.

Figure 6 shows $ {\rm d}v_{1}/{\rm d}y $ as a function of centrality for $ \pi^{+} $, $ K^{+} $, p, and their antiparticles in Au+Au and Cu+Cu collisions at $ \sqrt{s_{{NN}}} = 19.6 $ GeV. Results with and without the popcorn mechanism are shown. Note that the popcorn process increases the magnitude of $ {\rm d}v_{1}/{\rm d}y $ for $ K^{+} $, p, and $ \bar{p} $, while the effect on pions is small. In contrast, for 0–10% and 10%–40% collisions, a sign reversal is observed in $ {\rm d}v_{1}/{\rm d}y $ for $ K^{-} $ when the popcorn mechanism is enabled. Comparing the smaller Cu+Cu system to the larger Au+Au system, pions and, to a large extent, kaons do not exhibit substantial changes in $ {\rm d}v_{1}/{\rm d}y $, whereas protons (and anti-protons) show a more pronounced effect. For ultra-central collisions, the directed flow is expected to vanish owing to the absence of longitudinal asymmetry. We observed that for pions and kaons, $ {\rm d}v_{1}/{\rm d}y $ becomes nearly zero for $ b<1 $ fm/c, whereas protons and antiprotons exhibit a considerable magnitude. The non-zero magnitude of p ($ \bar{p} $) may be related to contributions from transported baryons or event-by-event asymmetries in baryon transport, requiring further investigation.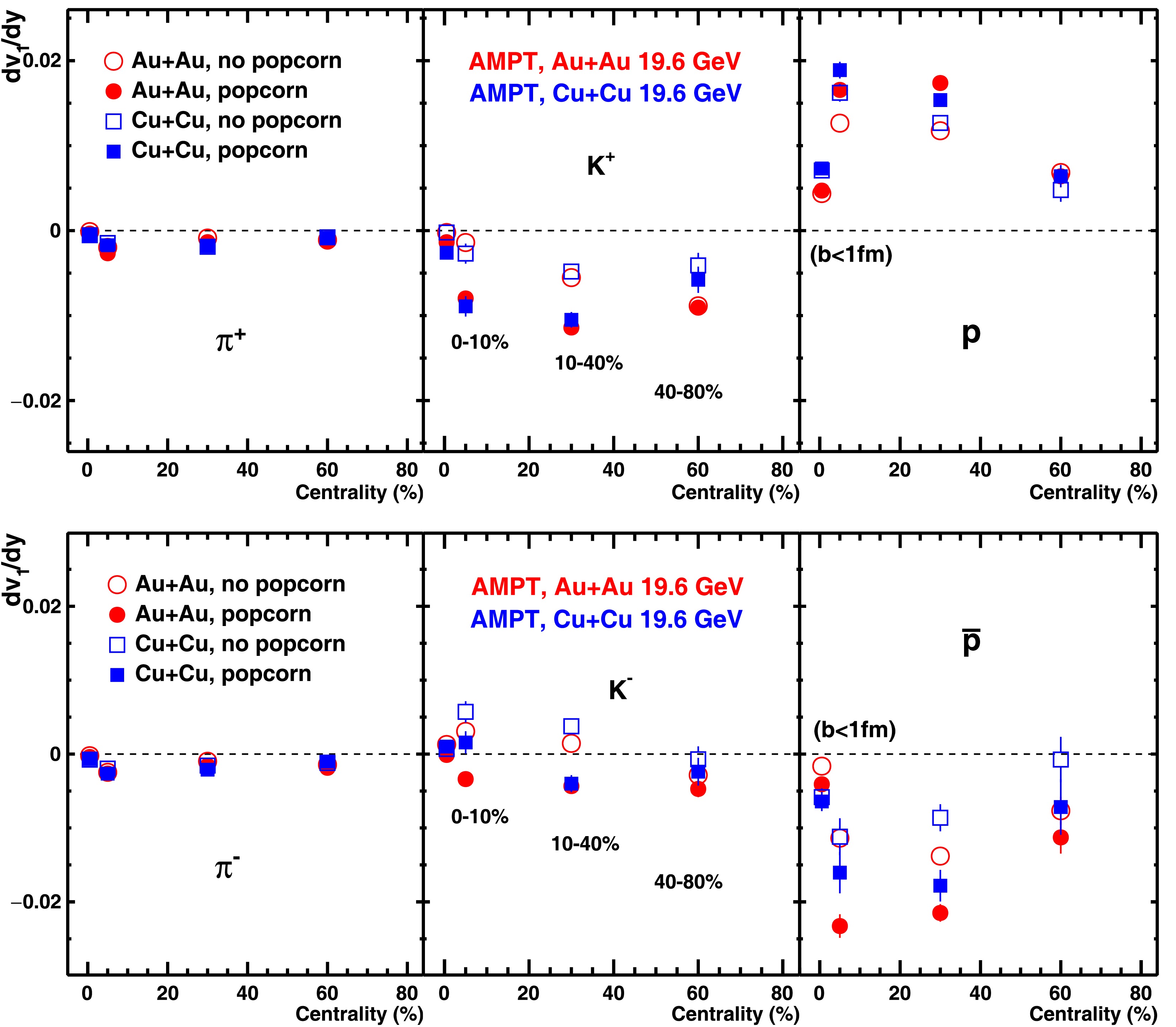

Figure 6.  (color online) ${\rm d}v_{1}/{\rm d}y$ for $\pi^{+}$, $K^{+}$, and $p$ and their antiparticles in Au+Au and Cu+Cu collisions at $\sqrt{s_{NN}}$ = 19.6 GeV for different collision centralities with and without popcorn mechanism (Table 1: set-1 and set-3) using the AMPT model. The model points at centrality = 0.5 correspond to ultra-central events ($b<1$ fm/c).

Figure 7 presents the differences in $ {\rm d}v_{1}/{\rm d}y $ for positive and negative particles, expressed as $ \Delta {\rm d}v_{1}/{\rm d}y $, as a function of centrality for π, K, and p in Au+Au and Cu+Cu collisions. The value of $ \Delta {\rm d}v_{1}/{\rm d}y $ for pions is small in magnitude, while for kaons, it is negative. For protons, however, the $ \Delta {\rm d}v_{1}/{\rm d}y $ value is positive and exhibits a clear centrality dependence, with a maximum observed in mid-central (10%–40%) collisions. In the same 10%–40% centrality range, the values of $ \Delta {\rm d}v_{1}/{\rm d}y $ for protons are larger in Au+Au collisions compared to those in Cu+Cu collisions. In contrast, the value of $ \Delta {\rm d}v_{1}/{\rm d}y $ for pions does not exhibit system-size dependence. For kaons, an opposite system size ordering to that of protons is observed: the magnitude of $ \Delta {\rm d}v_{1}/{\rm d}y $ in Cu+Cu is larger than in Au+Au, especially in central collisions, while in peripheral collisions, no evident system size dependence is observed.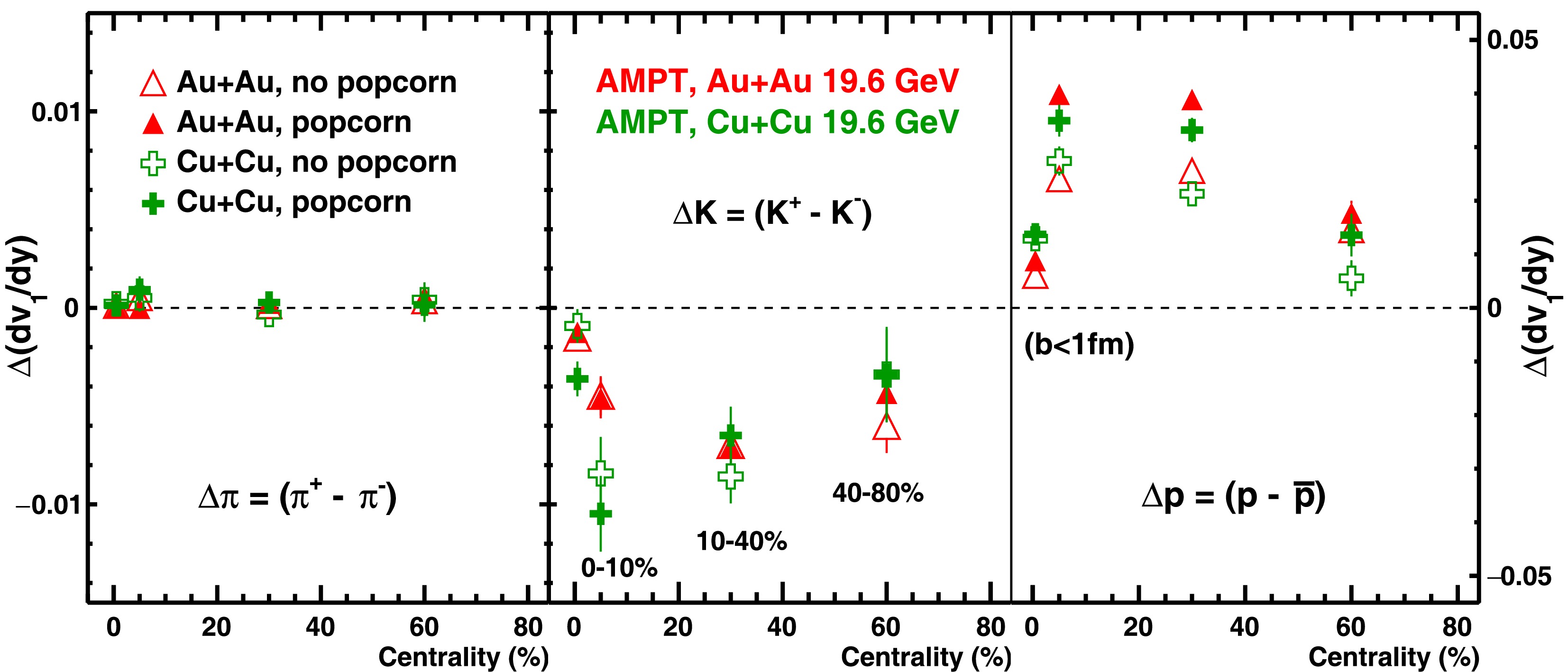

Figure 7.  (color online) $\Delta {\rm d}v_{1}/{\rm d}y$ for π, $K$, and $p$ in Au+Au and Cu+Cu collisions at $\sqrt{s_{NN}}$ = 19.6 GeV for different collision centralities with and without the popcorn mechanism (Table 1: set-1 and set-3), using the AMPT model. The model points at centrality = 0.5 correspond to ultra-central events ($b<1$ fm/c).

Next, we examined the effect on $ {\rm d}v_{1}/{\rm d}y $ and $ \Delta {\rm d}v_{1}/{\rm d}y $ for the aforementioned particles by varying the Lund string fragmentation parameter a in both Au+Au and Cu+Cu collisions; the results are presented in Fig. 8. As the value of a increases from 0.55 to 2.2, the magnitude of $ {\rm d}v_{1}/{\rm d}y $ increases for $ K^{-} $, p, and $ \bar{p} $, whereas $ K^{+} $ exhibits a decreasing trend. In contrast, $ \pi^{\pm} $ remain unaffected by this variation. The effect of the parameter a on $ \Delta {\rm d}v_{1}/{\rm d}y $ is shown in Fig. 9. With the increase in a, the magnitude of $ \Delta {\rm d}v_{1}/{\rm d}y $ decreases for kaons, increases for protons, and remains largely unchanged for pions.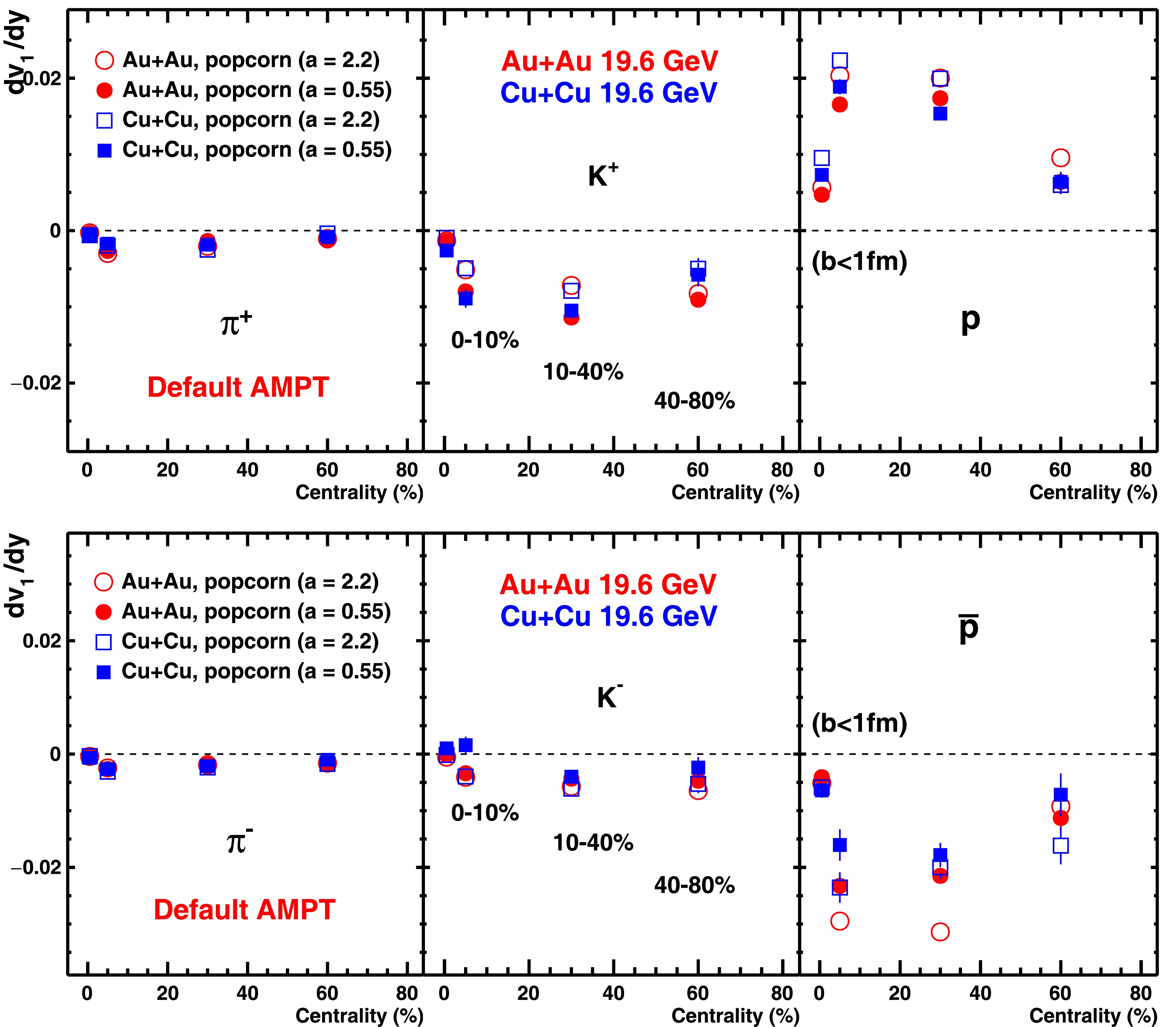

Figure 8.  (color online) ${\rm d}v_{1}/{\rm d}y$ for $\pi^{+}$, $K^{+}$, and $p$ and their antiparticles in Au+Au and Cu+Cu collisions at $\sqrt{s_{NN}}$= 19.6 GeV for different collision centralities, two cases of the popcorn mechanism, and Lund fragmentation parameter values a=0.55 and a=2.2 (Table 1: set-3 and set-4), using the AMPT model. The model points at centrality = 0.5 correspond to ultra-central events ($b<1$ fm/c).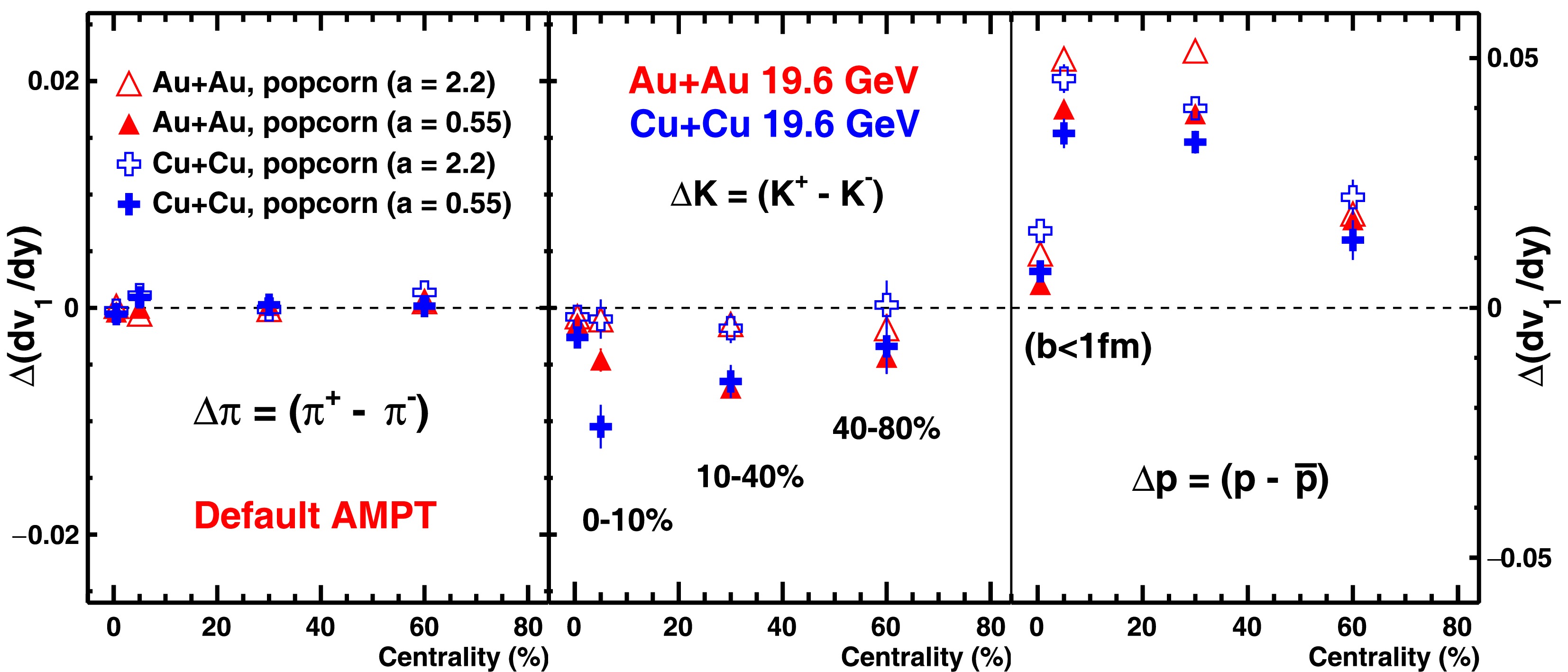

Figure 9.  (color online) $\Delta {\rm d}v_{1}/{\rm d}y$ for π, $K$, and $p$ in Au+Au and Cu+Cu collisions at $\sqrt{s_{NN}}$= 19.6 GeV for different collision centralities, two cases of the popcorn mechanism, and Lund fragmentation parameter values a=0.55 and a=2.2 (Table 1: set-3 and set-4), using the AMPT model. The model points at centrality = 0.5 correspond to ultra-central events ($b<1$ fm/c).

Furthermore, we analyzed the variation of $ {\rm d}v_{1}/{\rm d}y $ and $ \Delta {\rm d}v_{1}/{\rm d}y $ in Au+Au and Cu+Cu collisions as a function of the average number of participating nucleons ($ \langle N_{\rm part} \rangle $), as shown in Figs. 10 and 11. At small $ \langle N_{\rm part} \rangle $ values, $ {\rm d}v_{1}/{\rm d}y $ and $ \Delta {\rm d}v_{1}/{\rm d}y $ for all particles approximately scale with $ \langle N_{\rm part} \rangle $, but this scaling breaks down at large values of $ \langle N_{\rm part} \rangle $.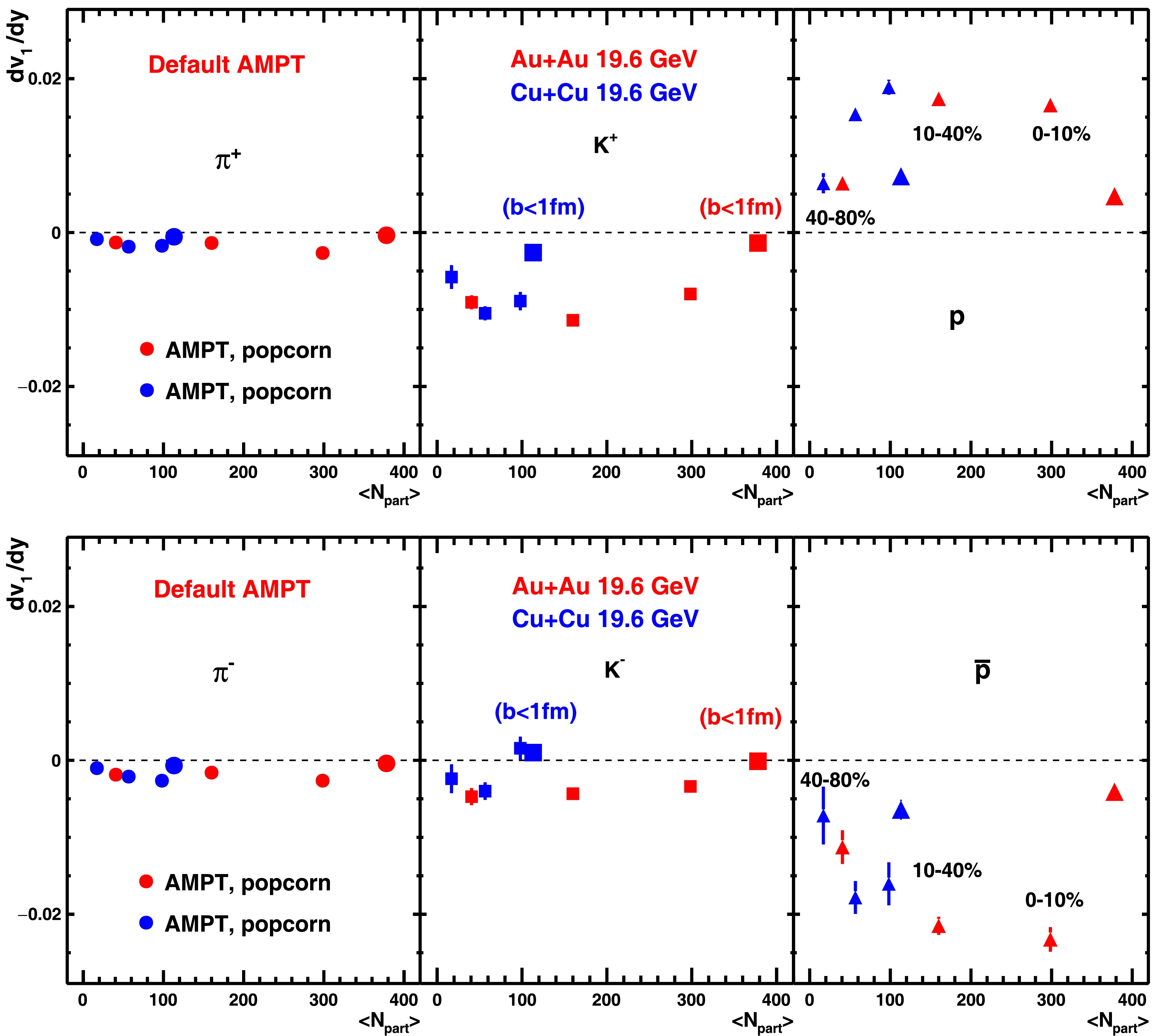

Figure 10.  (color online) ${\rm d}v_{1}/{\rm d}y$ for π, $K$, and $p$ and their antiparticles in Au+Au and Cu+Cu collisions as a function of the average number of participants ($\langle N_{\rm part} \rangle$) at $\sqrt{s_{NN}}$ = 19.6 GeV with popcorn mechanism (Table 1: set-3) using the AMPT model. The model points with larger marker size correspond to ultra-central events ($b<1$ fm/c).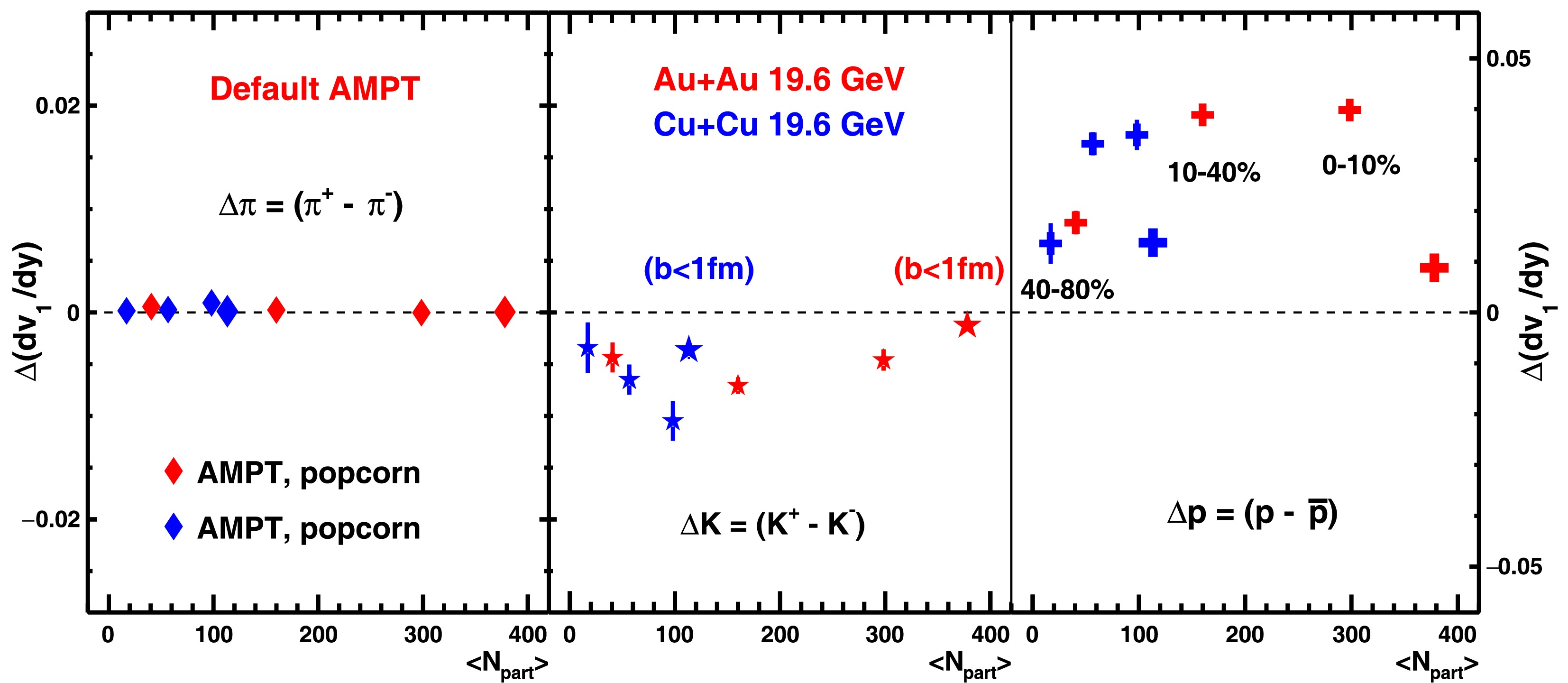

Figure 11.  (color online) $\Delta {\rm d}v_{1}/{\rm d}y$ for π, $K$, and $p$ in Au+Au and Cu+Cu collisions as a function of the average number of participants ($\langle N_{\rm part} \rangle$) at $\sqrt{s_{NN}}$ = 19.6 GeV with the popcorn mechanism (Table 1: set-3), using the AMPT model. The model points with larger marker size correspond to ultra-central events ($b<1$ fm/c).

We present measurements of pseudorapidity distributions ($ {\rm d}N/{\rm d}y $) and directed flow ($ v_1 $) for pions, kaons, and protons in Au+Au and Cu+Cu collisions at $ \sqrt{s_{{NN}}} = 19.6 $ GeV, using the AMPT model. The string junction parameters in AMPT, specifically the popcorn mechanism and string splitting parameter, were tuned to modify the production and yield of pions, kaons, and protons near mid-rapidity. By leveraging the string fragmentation mechanism and varying its parameters, we observed changes in the fraction of net particles near mid-rapidity.

When the popcorn mechanism was enabled, we observed an increase in both $ {\rm d}N/{\rm d}y $ and the magnitude of $ {\rm d}v_{1}/{\rm d}y $ for protons, as well as in $ \Delta {\rm d}N/{\rm d}y $ and $ \Delta {\rm d}v_{1}/{\rm d}y $ for protons ($ \Delta p $), within collision systems such as Au+Au or Cu+Cu. For pions, $ {\rm d}N/{\rm d}y $ increases, but no appreciable change was observed in $ {\rm d}v_{1}/{\rm d}y $ or $ \Delta {\rm d}v_{1}/{\rm d}y $. In contrast, kaons exhibit non-trivial changes in both yield and $ {\rm d}v_{1}/{\rm d}y $.

When the string-splitting parameter a was increased from 0.5 to 2.2, the rapidity density $ {\rm d}N/{\rm d}y $ increased for all particle species. This change in a also enhanced the magnitude of $ {\rm d}v_{1}/{\rm d}y $ for p, $ \bar{p} $, and $ \Delta p $. However, $ {\rm d}v_{1}/{\rm d}y $ for $ K^{+} $ and $ \Delta K $ exhibited the opposite trend, that is, a decrease in magnitude, while pions remained largely unaffected.

Additionally, comparisons between different collision systems, such as Au+Au and Cu+Cu, reveal that both mechanisms, namely enabling the popcorn process and varying the string splitting parameter, can contribute to the system size dependence of $ {\rm d}v_{1}/{\rm d}y $ for protons at fixed centrality, along with a non-trivial effect on kaons, while pions remain largely unchanged across system sizes. These findings can provide valuable insights into particle production mechanisms and directed flow across different system sizes.

In the future, these studies can be extended to both higher and lower beam energies. Notably, none of the current models can simultaneously capture the negative values of $ \Delta {\rm d}v_{1}/{\rm d}y $ observed for pions, kaons, and protons, particularly at lower RHIC energies. While hydrodynamic models can reproduce this behavior for baryons, they fail to comprehensively describe the full range of experimental observations. To achieve a deeper understanding of the data, it is essential to develop advanced models that incorporate a combination of transport mechanisms, mean-field effects, and electromagnetic field interactions. Our study aims to explore the interplay among particle production processes, baryon transport, and directed flow in heavy-ion collisions.

We would like to thank our colleagues at the Institute of Modern Physics for many insightful discussions. Authors would also like to acknowledge discussions with Sandeep Chatterjee and Tribhuban Parida during this study.