Improvement of nuclear semi-empirical mass formula by including shell effect

Nuclear mass is one of the most fundamental physical quantities in nuclear physics [1, 2], which has been widely used to extract nuclear effective interactions [3−6] and various nuclear structure information, such as nuclear pairing correlation [7], shell effect [8, 9], and deformation [10, 11]. From nuclear mass, one can easily calculate the various nucleon separation, reaction, and decay energies, which determine the positions of the drip lines [12] and are a key input to rapid-neutron capture process simulations (r-process). The uncertainty in the nuclear mass has a large influence on the β-decay half-lives [13] and neutron capture rates [14], which significantly affects the abundance distributions in the r-process simulations [15−17]. The β-decay half-life calculations with the consideration of first-forbidden transitions also show the significant impact of mass predictions on half-life calculations and the abundance distributions in the r-process simulations [18]. In conclusion, nuclear mass plays an important role in both nuclear physics and nuclear astrophysics [19−21].

Various theoretical models predict more than $ 7000 $ nuclei on the nuclear chart [22−25], but only approximately $ 3000 $ nuclear masses have been experimentally measured [26], and many of the nuclear masses involved in r-process simulations remain unmeasured. This increases the necessity to develop mass models with reliable extrapolation abilities. To date, various mass models have been developed with root mean square (rms) deviations in the range of $ 0.3\sim3 $ MeV. There are mainly three kinds of nuclear mass models: macroscopic, microscopic, and macroscopic-microscopic models.

The earliest nuclear mass model was the traditional liquid-drop model, i.e., Bethe-Weizsäcker (BW) semi-empirical formula, which is a macroscopic model that treats the nucleus as a charged liquid drop [27, 28]. Because it does not take into account microscopic shell corrections, there are large deviations between the nuclear mass predictions and experimental data around magic nuclei, and then the BW formula was developed by including various correction terms [29, 30]. The rms deviation of the improved BW formula reaches approximately $ 1.6 $ MeV. Based on the macroscopic model, the Strutinsky method [31] is used to extract the shell correction energies, further developing macroscopic-microscopic models. For example, the finite-range droplet model (FRDM) [32, 33] has an rms deviation of approximately $ 0.6 $ MeV with respect to the experimental mass data and is often used as input to r-process simulations. In addition, a series of Weizsäcker-Skyrme (WS) models have been developed by taking into account isospin effects [34], mirror nuclei constraints [35], and surface diffuseness effects (WS4) [36]. The WS4 mass model has an rms deviation of approximately $ 0.3 $ MeV. However, it is difficult for macroscopic-microscopic models to ensure self-consistency between macroscopic and microscopic terms. Microscopic models study atomic nuclei at the nucleon level and can give various nuclear ground-state properties, including nuclear mass, in a uniform framework [37]. Therefore, they are often believed to have a more reliable extrapolation ability. In a non-relativistic framework, a series of Hartree-Fork-Bogoliubov (HFB) microscopic mass models have been developed with a rms deviation of $ 0.5\sim0.8 $ MeV by using Skyrme [38, 39] or Gogny forces [40]. Microscopic mass models in the relativistic framework include relativistic mean-field (RMF) models [41, 42], Relativistic-Continuum-Hartree-Bogoliubov (RCHB) [22], and deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) [23, 24, 43]. For these relativistic microscopic mass models, the accuracy with respect to the experimental data now reaches nearly 1 MeV [23, 24, 42]. It should be noted that the DRHBc mass tables are currently only available for the even-even nuclei [23] and even-Z nuclei [24], as DRHBc calculations are very time consuming due to the inclusion of continuum effects.

In recent years, with the rapid development of artificial intelligence, machine learning (ML) methods have also been widely used to study nuclear properties [44−46], such as α-decay half-lives [47, 48], β-decay half-lives [49−52], fission yields [53, 54], charge radii [55, 56], and nuclear reaction cross-sections [57−60]. To date, ML methods such as Bayesian neural network (BNN) [61−63], kernel ridge regression (KRR) [64, 65], Light Gradient Boosting Machine (LigthGBM) [66], and Gaussian process [67] have been used to study nuclear mass; the rms deviation of mass models based on these ML methods with respect to the experimental data reaches approximately $ 0.1 $ MeV. Although ML models have high prediction accuracy in the known region, the physics basis of ML methods is unclear, which may affect their extrapolation abilities [68]. For example, the radial basis function (RBF) [69, 70] and KRR methods were found to have reliable extrapolation distances not far from the known region [71]. Recently, physics-informed ML and fully connected neural networks have been developed to study nuclear mass predictions, which can largely reduce the discrepancy between theory and experiment by directly learning model binding energy residuals or employing a multi-output training strategy [72, 73].

This study focuses on constructing shell correction terms to improve the prediction ability of the semi-empirical mass formula for magic nuclei. Each term in the semi-empirical mass formula has a clear physical meaning, and it is easy to know the specific contribution of each term to the binding energy. In addition, its high efficiency and low computational cost make it possible to calculate all nuclear masses in a very short time, which is highly useful for systematically studying the uncertainties and sensitivities of the r-process. Our mass formula has an rms deviation of 0.887 MeV with respect to the experimental data in AME2020 [26] for nuclei with $ Z,\; N \geqslant 8 $, which induces a 72.23% reduction compared to the BW formula and 45.42% lower than the rms deviation of the empirical formula proposed in Ref. [29]. In particular, the mass predictions are significantly improved for magic nuclei.

The remainder of this paper is organized as follows. Section II introduces the BW semi-empirical mass formula and construction of the shell correction terms. The results and discussion are presented in Sec. III. Finally, a summary and future prospects are given in Sec. IV.

The traditional BW semi-empirical mass formula takes into account the volume energy, surface energy, Coulomb energy, and symmetry energy. The binding energy B for a nucleus with proton number Z and neutron number N (mass number $ A = Z + N $) can be calculated from the following four terms:

where $ \alpha_{i} $ denotes the free parameters determined by fitting the experimental nuclear masses. In Ref. [29], the exchange Coulomb term $ \alpha_{xc}Z^{4/3}A^{-1/3} $, Wigner term $ \alpha_w\lvert N-Z\rvert A^{-1} $, pairing term $ \delta\alpha_pA^{-1/2} $, surface symmetry term $ \alpha_{st}(N-Z)^2A^{-4/3} $, curvature term $ \alpha_rA^{1/3} $, and shell correction terms $ \alpha_mP+\beta_mP^2 $ based on the BW formula were added. In this paper, this model is denoted as the BWK mass formula. In the above expressions, δ and P are given by

where $ \nu_p $ and $ \nu_n $ are the numbers of valence nucleons, i.e., the differences between the nucleon numbers Z and N and the nearest magic number, respectively (the proton and neutron magic numbers are taken to be $ 2,\; 8,\; 20,\; 28,\; 50,\; 82,\; 126 $ and $ 2,\; 8,\; 20,\; 28,\; 50,\; 82,\; 126,\; 184 $ as in Ref. [29]). The new formula obtained by removing the shell correction terms $ \alpha_mP+\beta_mP^2 $ from the BWK formula is denoted as BWK*.

In Fig. 1, we investigate the effect of the shell correction terms $ \alpha_mP+\beta_mP^2 $ in the BWK formula on the predictions of binding energies. In general, the term gives a large improvement in the predictions of binding energies, causing a reduction of the rms deviation by approximately $ 0.8 $ MeV; in particular, it improves the predictions of the binding energies of some deformed nuclei, such as those in the regions $ 32\lesssim Z \lesssim 41 $, $ 34\lesssim N \lesssim45 $ and $ 34\lesssim Z \lesssim 47 $, $ 57\lesssim N \lesssim73 $. In addition, the BWK formula also improves the prediction ability of the binding energies for some magic nuclei with $ N = 28,\; 50 $. However, the predictions of the BWK formula have been worse for nuclei with $ Z\approx $ 50, 82, overestimating the experimental binding energies as above 4 MeV, while the predictions for some doubly magic nuclei are underestimated by more than 4 MeV. Moreover, the shell correction energies between semi-magic and doubly magic nuclei should be different, while the shell correction terms $ \alpha_mP+\beta_mP^2 $ are always 0 for both semi-magic and doubly magic nuclei. Thus, it is necessary to construct a new shell correction term that reflects the difference in shell correction energies between semi-magic and doubly magic nuclei.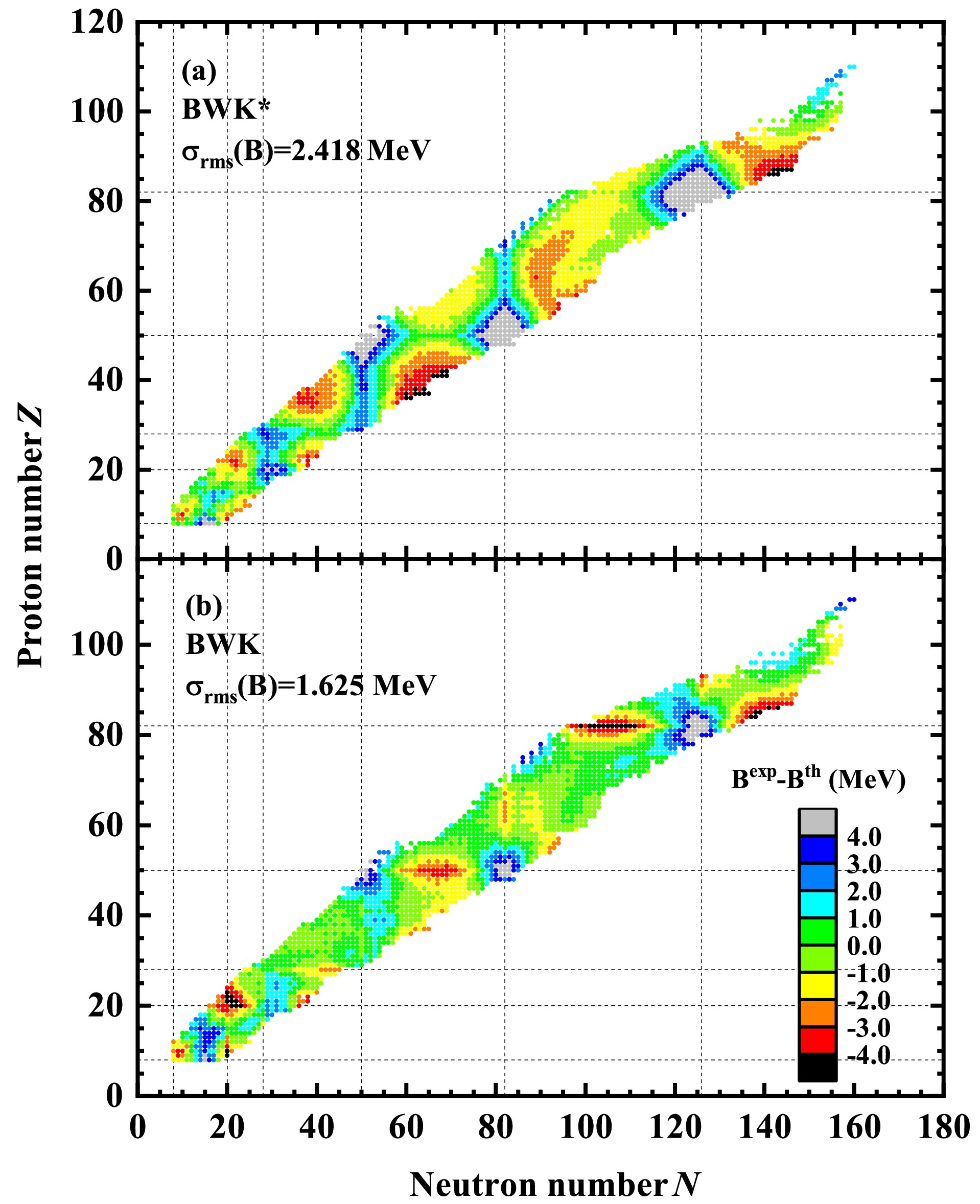

Figure 1.  (color online) Differences between the experimental binding energies and predictions calculated using the BWK* and BWK formulas, respectively. The dashed lines denote the traditional magic numbers.

To construct appropriate shell correction terms for magic nuclei, we study the differences between the experimental binding energies of near-magic nuclei and the BWK predictions with respect to the number of valence nucleons, as shown in Fig. 2. The binding energy residuals of the BWK formula are found to have an approximately linear relationship with the number of valence nucleons when the mass number $ A \geqslant 56 $. Therefore, the linear term of valence nucleons $ c_m(\nu_n+\nu_p) $ is used to describe the residuals of the semi-magic nuclear binding energy. The new formula is denoted as F1, and the form is as follows: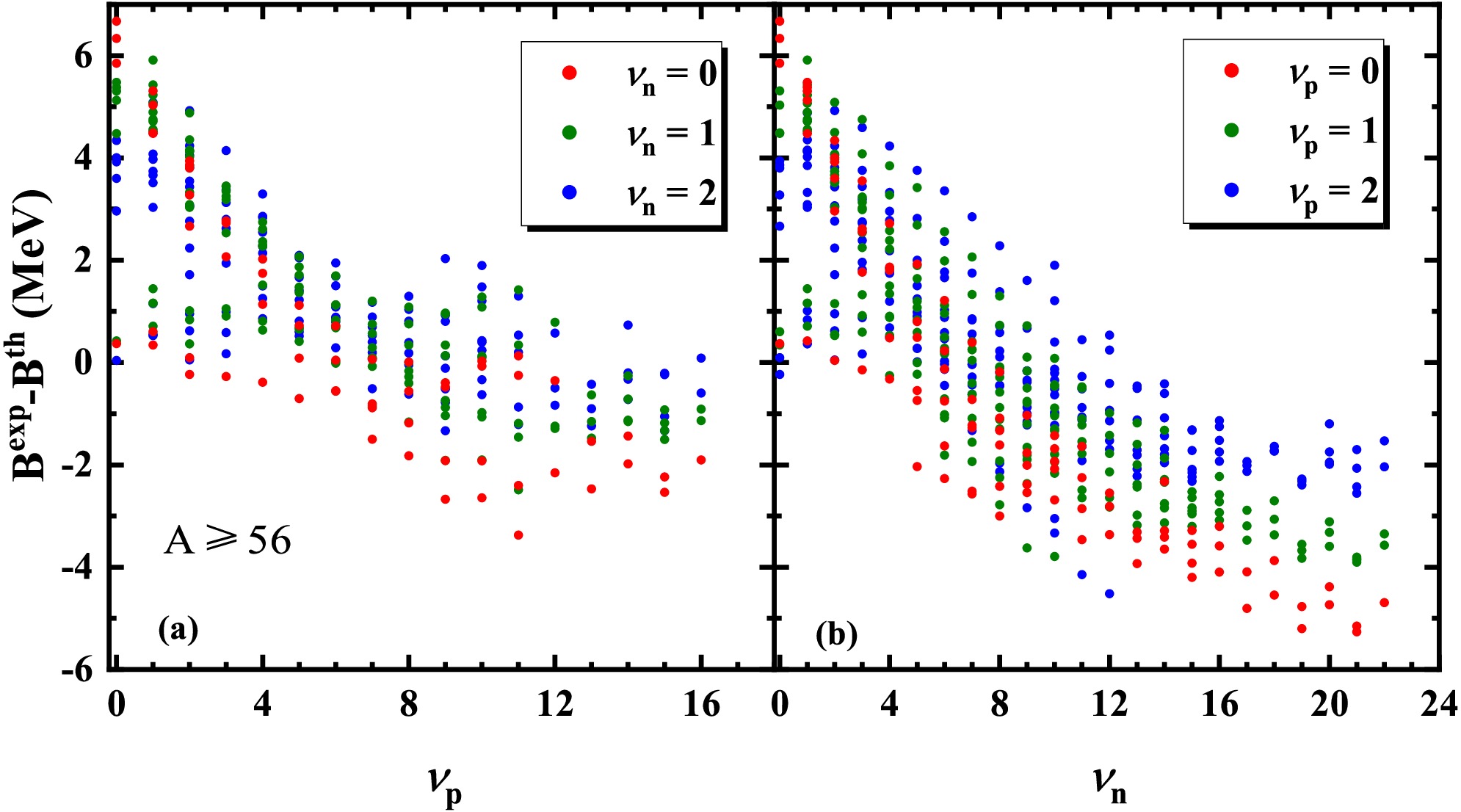

Figure 2.  (color online) Binding energy differences between the experimental data and predictions calculated with the BWK formula for nuclei with $A \geqslant 56$ as a function of $\nu_p $ (a) and $\nu_n $ (b) when the number of valence nucleons is 0 (red solid circle), 1 (green solid circle), and 2 (blue solid circle).

It is found that the linear term $ c_m(\nu_n+\nu_p) $ has very little effect on the prediction of the binding energy for nuclei with $ A < 56 $. To make the formula more universal, the linear term is used to improve the description of the binding energy for all nuclei with $ Z, N \geqslant 8 $.

It can be seen from Fig. 1(b) that the residuals between the experimental binding energies and predictions calculated with the BWK formula are largest near the doubly magic nuclei and decrease away from them. The exponential term $ e_{m1}e^{e_{m2}(\nu_p^2+\nu_n^2)} $ is introduced to describe such residuals for doubly magic nuclei, similar to Refs. [74, 75], where $ e_{m1} $ is expected to be positive and represents the shell correction energies of the doubly magic nuclei, and $ e_{m2} $ is expected to be negative such that the term gradually decays to 0 when moving away from the magic number. The new formula with exponential term $ e_{m1}e^{e_{m2}(\nu_p^2+\nu_n^2)} $ is denoted as F2*. The isospin dependence is further introduced in the F2* formula as in Ref. [36]; the new formula is denoted as F2. The specific expressions of F2* and F2 mass formulas are

where $ \alpha_{{\rm sym}\_I},\; I $, $ f_s $, and $ \delta_{np} $ are defined as

It is worth noting that the symmetry energy term with isospin dependence in Eq. (6) can be expanded by three terms: symmetry energy term, surface symmetry term, and Wigner term. From Fig. 1(b), it can be seen that the residuals of doubly magic nuclei are negative in the light-mass region, positive in the heavy-mass region, and near zero in the medium-mass region. In addition, we have tried many improvement methods and found that the corresponding binding energy residuals always show the same phenomenon. This means that the residuals of the binding energies are different for the magic nuclei in different regions. To describe the differences between the magic nuclei of different regions, a $ \delta_{\rm shell} $ in the coefficient of the exponential term is introduced, and the new formula obtained is named BWN, whose expression is

where

The parameters and corresponding uncertainties of semi-empirical formulas, i.e., BW, BWK*, BWK, F1, F2*, F2, and BWN, are obtained by performing a least squares fit on the experimental data for nuclei with $ Z,\; N \geqslant 8 $ in AME2020 [26], as shown in Tables 1 and 2. The mass tables for the F1, F2*, F2, and BWN formulas are available as Supplemental Material of this paper. The accuracy of the semi-empirical formula is evaluated by the rms deviation, defined by

	BW	BWK	BWK*	F1
$ \alpha_v/{\rm{MeV}} $	$ 15.5255 \pm 0.0242 $	$ 16.4920 \pm 0.0659 $	$ 16.1707 \pm 0.0954 $	$ 16.3845 \pm 0.0507 $
$ \alpha_s/{\rm{MeV}} $	$ -16.8949 \pm 0.0753 $	$ -25.5618 \pm 0.4630 $	$ -23.5820 \pm 0.6695 $	$ -24.7173 \pm 0.3566 $
$ \alpha_c/{\rm{MeV}} $	$ -0.7022 \pm 0.0017 $	$ -0.7614 \pm 0.0031 $	$ -0.7408 \pm 0.0044 $	$ -0.7611 \pm 0.0024 $
$ \alpha_{\rm sym}(c_{\rm sym})/{\rm{MeV}} $	$ -22.9874 \pm 0.0603 $	$ -32.5777 \pm 0.3042 $	$ -31.7110 \pm 0.4440 $	$ -31.8596 \pm 0.2346 $
$ \alpha_p/{\rm{MeV}} $	$ - $	$ 11.0409 \pm 0.4608 $	$ 11.9953 \pm 0.6844 $	$ 11.1655 \pm 0.3543 $
$ \alpha_{xc}/{\rm{MeV}} $	$ - $	$ 1.6997 \pm 0.0743 $	$ 1.4587 \pm 0.1077 $	$ 1.8009 \pm 0.0572 $
$ \alpha_w/{\rm{MeV}} $	$ - $	$ -61.7229 \pm 2.8712 $	$ -57.7605 \pm 4.2667 $	$ -44.4585 \pm 2.2473 $
$ \alpha_{st}/{\rm{MeV}} $	$ - $	$ 61.1172 \pm 1.5853 $	$ 57.5972 \pm 2.3234 $	$ 55.2362 \pm 1.2273 $
$ \alpha_r/{\rm{MeV}} $	$ - $	$ 13.3315 \pm 0.7883 $	$ 10.0163 \pm 1.1482 $	$ 11.2350 \pm 0.6083 $
$ \alpha_m/{\rm{MeV}} $	$ - $	$ -2.0293 \pm 0.0419 $	$ - $	$ -1.1379 \pm 0.0389 $
$ \beta_m/{\rm{MeV}} $	$ - $	$ 0.1595 \pm 0.0045 $	$ - $	$ 0.1979 \pm 0.0036 $
$ c_m/{\rm{MeV}} $	$ - $	$ - $	$ - $	$ -0.3665 \pm 0.0089 $
$ e_{m1}/{\rm{MeV}} $	$ - $	$ - $	$ - $	$ - $
$ e_{m2} $	$ - $	$ - $	$ - $	$ - $
k	$ - $	$ - $	$ - $	$ - $
ξ	$ - $	$ - $	$ - $	$ - $
$ \kappa_s $	$ - $	$ - $	$ - $	$ - $
$ \sigma_{\rm{rms}}(B) $$ /{\rm{MeV}} $	$ 3.194 $	$ 1.625 $	$ 2.418 $	$ 1.250 $
$ \sigma_{\rm{rms}}(S_{n}) $$ /{\rm{MeV}} $	$ 1.335 $	$ 0.585 $	$ 0.639 $	$ 0.509 $
$ \sigma_{\rm{rms}}(S_{p}) $$ /{\rm{MeV}} $	$ 1.542 $	$ 0.614 $	$ 0.600 $	$ 0.507 $

Table 1.  Parameters with uncertainties and $ \sigma_{\rm rms} $ of the BW, BWK, BWK*, and F1 mass formulas.

	F2*	F2	BWN
$ \alpha_v/{\rm{MeV}} $	$ 16.1287 \pm 0.0482 $	$ 15.9108 \pm 0.0474 $	$ 16.7043 \pm 0.0398 $
$ \alpha_s/{\rm{MeV}} $	$ -21.9924 \pm 0.3502 $	$ -19.5107 \pm 0.3376 $	$ -26.3000 \pm 0.2824 $
$ \alpha_c/{\rm{MeV}} $	$ -0.7542 \pm 0.0023 $	$ -0.7404 \pm 0.0025 $	$ -0.7615 \pm 0.0020 $
$ \alpha_{\rm sym}(c_{\rm sym})/{\rm{MeV}} $	$ -31.3853 \pm 0.2205 $	$ -33.1442 \pm 0.3409 $	$ -35.3636 \pm 0.2648 $
$ \alpha_p/{\rm{MeV}} $	$ 11.4215 \pm 0.3248 $	$ 6.0387 \pm 0.1634 $	$ 5.9751 \pm 0.1303 $
$ \alpha_{xc}/{\rm{MeV}} $	$ 1.6434 \pm 0.0534 $	$ 1.2311 \pm 0.0592 $	$ 1.4405 \pm 0.0473 $
$ \alpha_w/{\rm{MeV}} $	$ -41.1184 \pm 2.0908 $	$ - $	$ - $
$ \alpha_{st}/{\rm{MeV}} $	$ 52.1968 \pm 1.1617 $	$ - $	$ - $
$ \alpha_r/{\rm{MeV}} $	$ 2.9261 \pm 0.6888 $	$ -2.1600 \pm 0.6452 $	$ 14.1287 \pm 0.4749 $
$ \alpha_m/{\rm{MeV}} $	$ -1.0094 \pm 0.0379 $	$ -1.0369 \pm 0.0369 $	$ -1.0877 \pm 0.0277 $
$ \beta_m/{\rm{MeV}} $	$ 0.1008 \pm 0.0058 $	$ 0.1052 \pm 0.0057 $	$ 0.1615 \pm 0.0028 $
$ c_m/{\rm{MeV}} $	$ 0.0399 \pm 0.0264 $	$ 0.0318 \pm 0.0257 $	$ -0.2343 \pm 0.0076 $
$ e_{m1}/{\rm{MeV}} $	$ 7.6167 \pm 0.4509 $	$ 7.3839 \pm 0.4407 $	$ 5.4713 \pm 0.1229 $
$ e_{m2} $	$ -0.0104 \pm 0.0004 $	$ -0.0103 \pm 0.0004 $	$ -0.0444 \pm 0.0020 $
k	$ - $	$ 1.9017 \pm 0.0417 $	$ 2.0829 \pm 0.0288 $
ξ	$ - $	$ 1.0950 \pm 0.0434 $	$ 1.2216 \pm 0.0313 $
$ \kappa_s $	$ - $	$ 0.2417 \pm 0.0405 $	$ 0.2491 \pm 0.0314 $
$ \sigma_{\rm{rms}}(B) $$ /{\rm{MeV}} $	$ 1.144 $	$ 1.111 $	$ 0.887 $
$ \sigma_{\rm{rms}}(S_{n}) $$ /{\rm{MeV}} $	$ 0.483 $	$ 0.417 $	$ 0.381 $
$ \sigma_{\rm{rms}}(S_{p}) $$ /{\rm{MeV}} $	$ 0.481 $	$ 0.450 $	$ 0.394 $

Table 2.  Parameters with uncertainties and $ \sigma_{\rm{rms}} $ of the F2*, F2, and BWN mass formulas.

where $ B^{\exp}_{i} $ and $ B^{\rm th}_{i} $ are the experimental binding energies and theoretical predictions, respectively. n is the number of experimental data for the nuclei with $ Z,\; N \geqslant 8 $.

The rms deviations of the binding energies and single-neutron (proton) separation energies calculated by each semi-empirical formula are shown in Tables 1 and 2. From Tables 1 and 2, it can be seen that the rms deviation of the newly proposed BWN formula is $ 0.887 $ MeV, which is 72.23% and $ 45.42 $% less than those of the BW and BWK formulas, respectively. Because the rms deviations of F2* and F2 formulas are similar, isospin dependence in the symmetry energy and pairing energy terms in the F2 formula does not improve the accuracy in the known region, although their differences may become large in the unknown region. Furthermore, compared with the F2 formula, the introduction of $ \delta_{\rm shell} $ in the BWN formula can reduce the rms deviation by approximately 0.2 MeV, which indicates the importance of employing different shell corrections in different mass regions. In addition, the BWN formula not only improves the description of the nuclear mass but also significantly improves the prediction accuracies of the single-neutron (proton) separation energy. Among these mass formulas, the BWN mass formula is the only one whose rms deviations with respect to both the experimental single-neutron and single-proton separation energies are below 0.4 MeV. As can be seen in Fig. 2, the coefficient of the linear term for the number of valence nucleons should be negative. However, it is noted that the parameters $ c_m $ in the F2* and F2 formulas are positive, which is opposite to the sign we expected. This indicates that the exponential term with a constant coefficient does not accurately describe the shell correction energies of magic nuclei. The constant coefficient exponential term may unreasonably provide a part of shell correction energies for semi-magic nuclei to some degree, which induces the sign of the parameter of the linear term to not match what we expected. In contrast, the BWN formula has more reasonable parameters by taking into account the difference in shell correction energies of magic nuclei with different masses. In addition, it is worth mentioning that compared with the BW formula, the introduction of the surface symmetry and exchange Coulomb terms leads the surface energy and Coulomb energy coefficients in the BWN formula to be slightly different from the corresponding coefficients in the BW formula.

The rms deviation can only roughly reflect the accuracy of a semi-empirical mass formula. To show more details, the differences between the experimental binding energies and predictions calculated by the F1, F2*, and F2 formulas are shown in Fig. 3. Compared with Fig. 1(b), it can be found from Fig. 3(a) that the introduction of the linear terms $ c_m(\nu_n+\nu_p) $ improves the prediction ability of the formula for nuclei with proton numbers around $ 50,\; 82 $ and reduces the rms deviation by approximately $ 0.4 $ MeV. From Fig. 3(a) and (b), it can be seen that the exponential term with a constant coefficient provides a slight improvement for some superheavy nuclei, such as nuclei with $ Z\geqslant82 $ and $ N\geqslant126 $, but does not significantly improve the prediction accuracy of binding energies for doubly magic nuclei. Furthermore, comparing Fig. 3(b) and (c), we find that the effect of the isospin dependence of the symmetric energy and pairing energy term on mass description is small in the known mass region, with the rms deviation decreasing by approximately $ 0.03 $ MeV.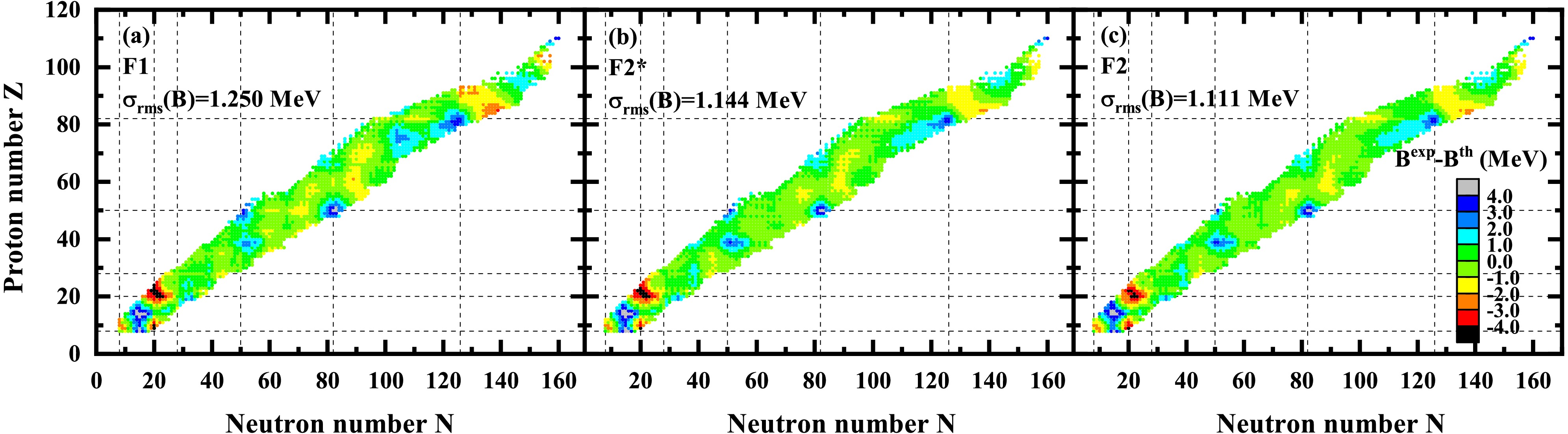

Figure 3.  (color online) Differences between the experimental binding energies and predictions calculated with the F1, F2*, and F2 formulas. The dashed lines denote the traditional magic numbers.

The mass description of the newly improved BWN formula is compared with the BW formula, as shown in Fig. 4. It can be seen that the binding energy predictions of the BW formula have large deviations from the experimental binding energies for magic nuclei and most deformed nuclei. Around the doubly magic nuclei, the predictions of the BW formula are always underestimated by more than 4 MeV compared to the experimental binding energies, while they are overestimated by more than 4 MeV in the deformation regions, such as $ 31\lesssim Z \lesssim39 $ and $ 35\lesssim N \lesssim47 $, $ 38\lesssim Z\lesssim47 $ and $ 55\lesssim N \lesssim69 $, and $ Z\gtrsim82 $ and $ N\gtrsim126 $. In addition, the binding energy residuals calculated by the BW formula (Eq. (1)) show odd-even staggering structures due to the lack of odd-even pairing correction, i.e., smaller and larger differences appear alternately. Compared to the BW formula, it can be seen from Fig. 4(b) that the BWN formula significantly improves the description of nuclear binding energies for nuclei near the magic numbers and the deformed nuclei. Based on the F2 formula, the BWN formula further takes into account the differences between doubly magic nuclei in different regions by introducing $ \delta_{\rm shell} $; its mass description is significantly improved in the region around the doubly magic nuclei, and the prediction accuracy of nuclear binding energies in the $ 8 < Z < 20,\; 8 < N < 20 $ region is also improved. The rms deviations of the predictions of the BWN formula with respect to the experimental binding energies are $ 0.887 $, $ 0.838 $, and $ 1.065 $ MeV for the three data sets: $ Z,\; N \geqslant 8, A \geqslant 60 $, and the magic nuclei, respectively, which is a reduction of 72.23%, 73.35%, and 80.08%, respectively, compared with the BW formula.

Figure 4.  (color online) Differences between the experimental binding energies and the predictions calculated with the BW and BWN formulas. The dashed lines denote the traditional magic numbers.

Figure 5 shows the differences between the experimental binding energies and predictions of the BW, BWK, and BWN mass formulas as a function of proton number and neutron number. The differences between the experimental binding energies and predictions of the BW mass formula are very large in the light nuclei region and in regions with proton numbers $ Z = 50,\; 82 $ or neutron numbers $ N = 50,\; 82,\; 126 $, even reaching more than $ 15 $ MeV. In addition to the region around traditional magic numbers, the large differences between experimental binding energies and the BW predictions are also found for some nuclei, such as those around $ Z = 34,\; 90 $ or $ N = 40,\; 145 $. By including other correction terms, the BWK formula reduces the binding energy residuals for most nuclei, but its predictions are not more accurate than BW for part nuclei, e.g., the nuclei with $ 100 \lesssim N \lesssim 120 $. Based on the BWK formula, the BWN formula is obtained by including new shell correction terms, and the descriptions of the nuclear mass is further improved for magic nuclei. The rms deviations of the BW and BWK formulas with respect to magic nuclei are $ 5.346 $ MeV and $ 2.734 $ MeV, respectively, while the corresponding rms deviation of the BWN formula is only $ 1.065 $ MeV, which is reduced by $ 80.08 $% and $ 61.04 $% compared to that of the BW and BWK formulas, respectively. In addition, the differences between the experimental binding energies and BWN predictions are almost always within $ 1.5 $ MeV. The percentages of nuclei for which the predictions of BW, BWK, and BWN deviate from the experimental data within $ 1.5 $ MeV are $ 41.88 $%, $ 70.53 $%, and $ 91.90 $%, respectively.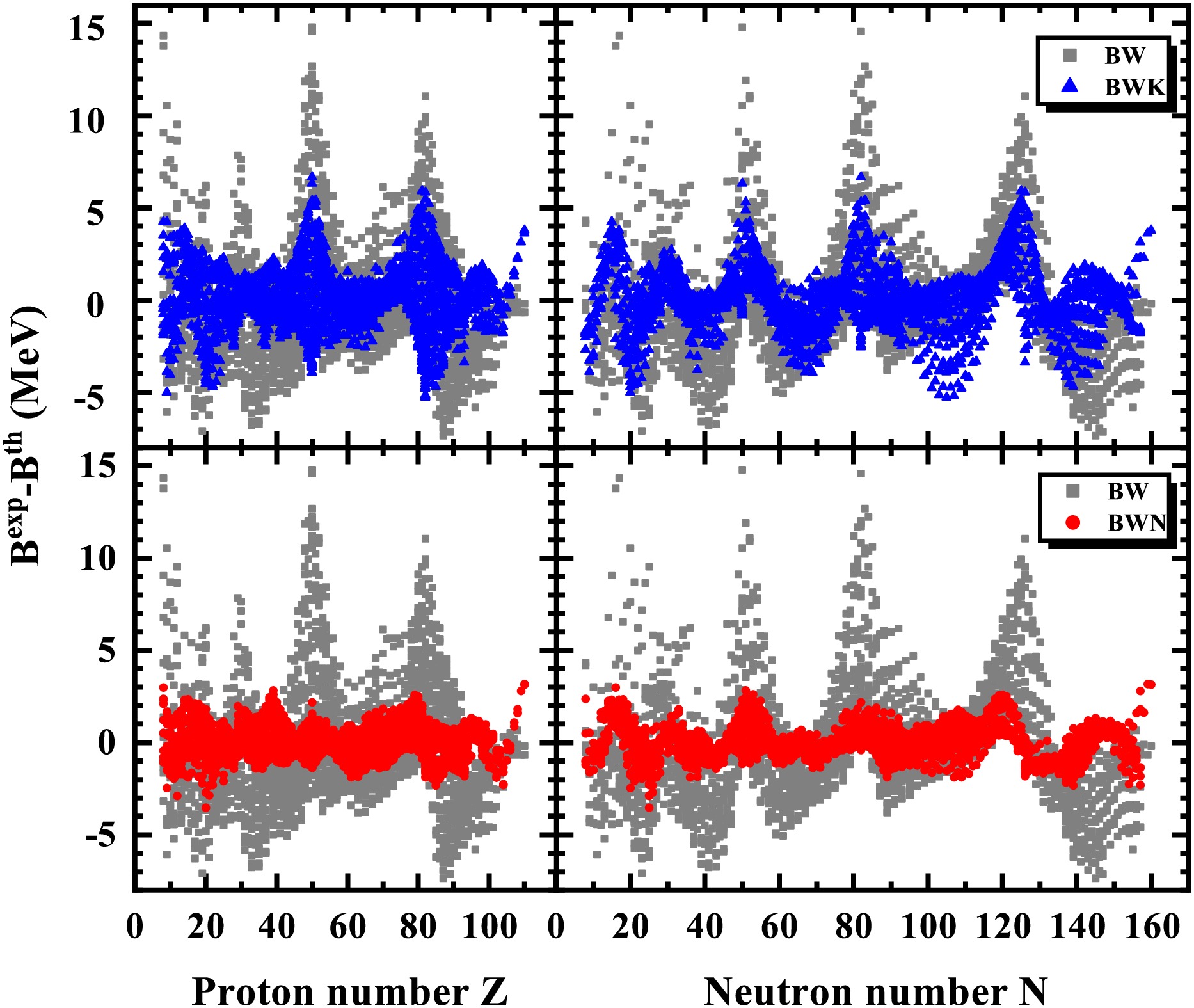

Figure 5.  (color online) Differences between the experimental nuclear binding energies and predictions calculated with the BW (grey squares), BWK (blue triangles), and BWN (red circles) formulas versus proton and neutron numbers.

The single-neutron separation energies $ S_n $ of the BW, BWK, and BWN mass formulas are shown in Fig. 6, taking the Ca, Ni, Sn, and Pb isotopes as examples. There is remarkable odd-even staggering for the $ S_n $ in each isotope. The $ S_n $ variation is smooth for the BW formula in Eq. (1) due to the ignorance of the pairing term, whereas the BWK and BWN formulas well reproduce the odd-even staggering. The experimental $ S_n $ shows a sudden decrease after the neutron magic numbers, e.g., $ S_n $ decreases sharply from $ 7.353 $ MeV for $ ^{132} $Sn to $ 2.399 $ MeV for $ ^{133} $Sn. The BWN formula better reproduces the $ S_n $ of nuclei with neutron magic numbers in the Sn and Pb isotopic chains than the BWK formula. Similarly, the single-proton separation energies $ S_p $ predicted by the BW, BWK, and BWN formulas for $ N = 20,\; 28,\; 50,\; 82,\; 126 $ isotones are shown in Fig. 7. It can be seen from Fig. 7 that both the BWK and BWN formulas reproduce the experimental $ S_p $ well, but the BWN formula better reproduces the experimental $ S_p $ near the proton magic numbers compared to the BWK formula. Therefore, the BWN formula shows better agreement with the experimental masses and separation energies compared to the BW and BWK formulas, particularly for nuclei around magic numbers.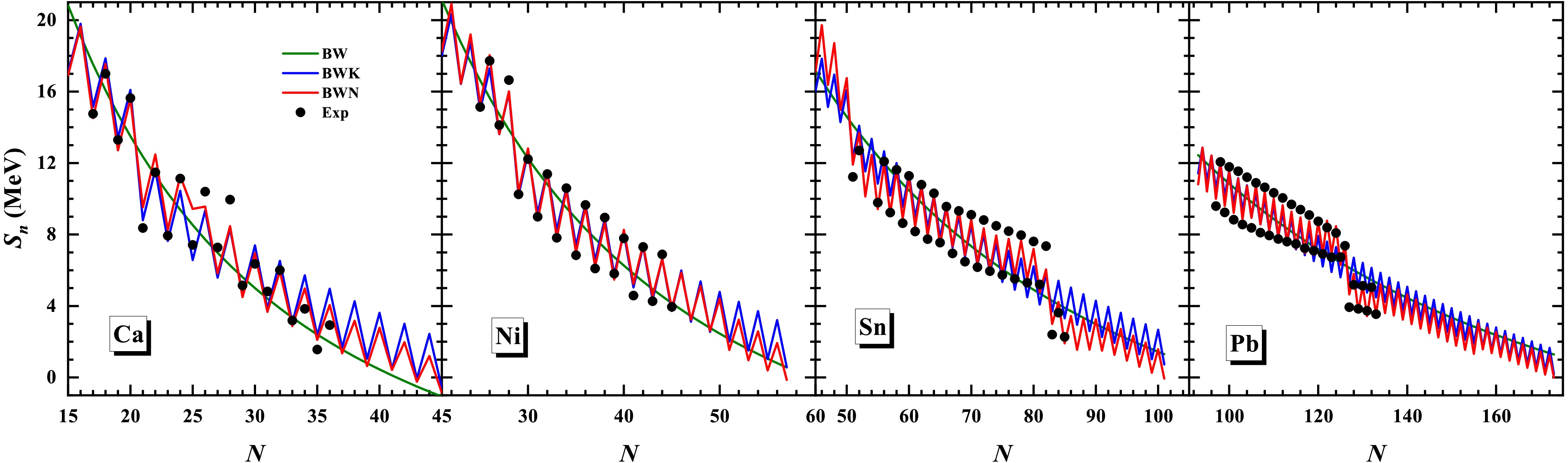

Figure 6.  (color online) Single-neutron separation energies of Ca, Ni, Sn, and Pb isotopes predicted by BW, BWK, and BWN. The experimental data from AME2020 are denoted by filled circles.

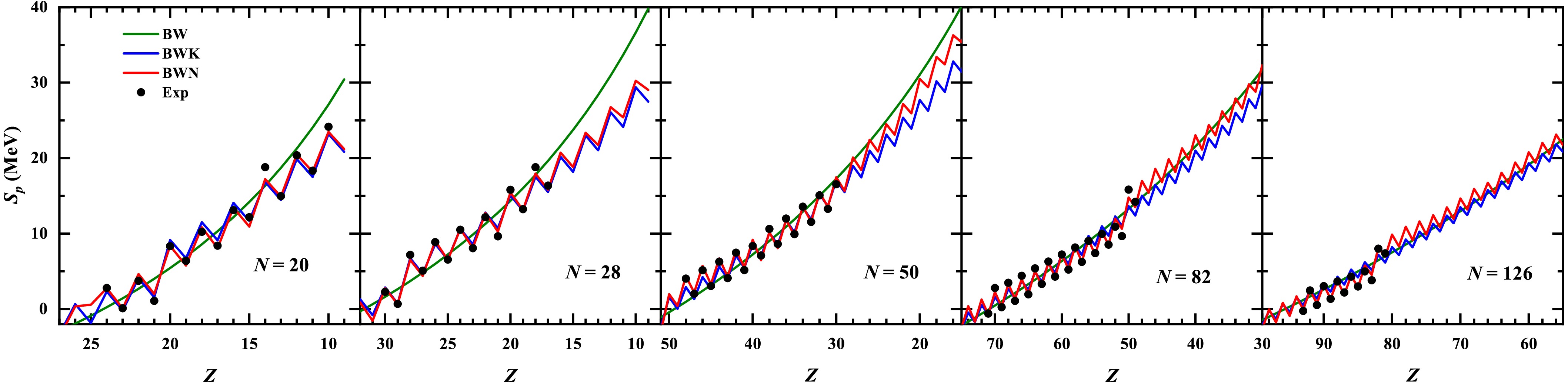
Figure 7.  (color online) Same as Fig. 6 but for single-proton separation energies $S_p$ of $N=20, 28, 50, 82, 126$ isotones.

In summary, a semi-empirical mass formula based on a liquid-drop model was improved by including new shell correction terms. The shell correction terms in the mass formula contain three components: the quadratic polynomial of P and the linear and exponential terms of valence nucleons. The quadratic polynomial terms of P improve the predictions of binding energy for most deformed nuclei and part magic nuclei. The linear term for the number of valence nucleons is used to improve the prediction ability of the mass formula for semi-magic nuclei, especially the nuclei with proton numbers near $ 50,\; 82 $, and reduces the rms deviation by approximately $ 0.4 $ MeV. The introduction of an exponential term with a constant coefficient did not obviously improve the prediction ability of the mass formula for doubly magic nuclei, but the binding energy residuals were significantly reduced for doubly magic nuclei by taking into account the differences between the different doubly magic nuclei, and the exponential term reduces the rms deviation by approximately $ 0.2 $ MeV. Compared with the BW and BWK mass formulas, the rms deviation of our mass formula with respect to experimental data for the nuclei with $ Z,\; N \geqslant 8 $ is reduced by $ 72.23 $% and $ 45.42 $%, respectively, falling $ 0.887 $ MeV. The rms deviation of the our formula with respect to magic nuclei is only $ 1.065 $ MeV, which is reduced by $ 80.08 $% and $ 61.04 $% compared to those of the BW and BWK formulas, respectively. In addition, nuclei with experimental binding energies that deviate from the predictions of BW, BWK, and our mass formula within $ 1.5 $ MeV account for 41.88%,70.53%, and $ 91.90 $% of the total number of nuclei, respectively. Besides the significant improvement in the description of nuclear mass, our mass formula also improves the predictions of mass differences, such as the single-neutron (proton) separation energy. In conclusion, our mass formula significantly improves the description of nuclear binding energies, especially for magic nuclei. In the future, we will further consider the effect of deformed effects on the binding energy. In addition, because the semi-empirical formula enables large-scale calculations of nuclear masses in a short time, it is well suited for studies of the sensitivity of r-process abundances to nuclear masses, which could deepen our understanding of the origin of heavy elements.