Investigating the transverse-momentum- and pseudorapidity-dependent flow vector decorrelation in p--Pb collisions with a Multi-Phase Transport model

High-energy heavy-ion collisions, such as those at the Relativistic Heavy-Ion Collider (RHIC) and the Large Hadron Collider (LHC) [1−8], offer an unique opportunity to study the nuclear matter under extreme conditions of temperature and density. These collisions create the quark-gluon plasma (QGP) [9, 10], a state of matter where quarks and gluons are no longer confined within hadrons but instead form a hot, dense medium. One of the most important observable for the formation of the QGP is the azimuthal anisotropy of produced particles, which is typically characterized by the Fourier expansion of the hadron yield distribution as a function of azimuthal angle φ:

where the Fourier coefficient $ v_{n} $ and symmetry plane angle $ \Psi_{n} $ represent the magnitude and orientation of the $ n^{th} $ order flow vector $ V_{n}\equiv v_{n}e^{in\Psi_{n}} $ [11, 12]. Plenty of measurements focusing on the the second harmonic flow $ v_{2} $ (elliptic flow), have been performed at the both RHIC [13−17] and LHC [18−28]. The comparisons to theoretical model calculations provided unprecedented constraints on the fundamental transport properties of the QGP medium [29−32], such as the ratio of shear viscosity to entropy density (η/s), which indicate that the QGP created in heavy-ion collisions behaves as a nearly perfect fluid.

Due to the event-by-event fluctuations in the initial energy density of the nuclear collisions [29, 33], the fluctuations of second order flow vector $ V_{2} $, as well as its transverse-momentum ($ \it{p}_{\mathrm{T}} $) dependence have been shown in hydrodynamical models [34−36]. These fluctuations could result in the breakdown of factorization of two-particle angular correlations into a product of single-particle flow coefficients in different $ \it{p}_{\mathrm{T}} $ intervals [34, 37−40], which were discovered in Pb–Pb collisions by the ALICE and CMS Collaborations [41−44]. In addition, the flow vector fluctuations along the pseudorapidity (η) direction was investigated by hydrodynamic and parton transport models, where the factorization breakdown in η was found to be sensitive to event-plane fluctuations at different η [45−48]. The LHC experiments measured the ratio of two-particle Fourier coefficients in rapidity bins η and $ -\eta $ [42, 49, 50], and the results show that the longitudinal fluctuations lead to a linear decrease of the ratio with η, i.e. the longitudinal flow decorrelations. These studies provide further constraint on the initial conditions and new insights to the longitudinal evolution of the medium formed in heavy ion collisions.

In recent years, the observation of non-zero $ v_{2} $ in p–Pb and pp collisions [51−59] raised the question of whether hydrodynamic flow also exists in these small collision system. The extracted flow harmonics in p–Pb collisions have been studied in detail as a function of $ \it{p}_{\mathrm{T}} $, η and event multiplicity [54, 60]. On the other hand, the fluctuations of flow vector as a function of $ \it{p}_{\mathrm{T}} $ and η in small collision systems are measured by the LHC experiments [41, 42, 50, 57]. The effect of factorization breakdown was observed in p–Pb collisions and much smaller than that in Pb–Pb collisions. The measurements of longitudinal flow decorrelations were even extended to the smaller pp collisions by the ATLAS Collaboration [57], and the results reveal significant sensitivity to the nonflow correlations. Since the origin of collective flow in small collision systems remains unclear [61], there are significant uncertainties in the study of $ \it{p}_{\mathrm{T}} $ and η-dependent flow vector decorrelations in these systems. The study based on the event-by-event hydrodynamic calculations demonstrated the important role of longitudinal decorrelations in small collision systems, and predicted rapidity-asymmetric flow decorrelations across different colliding energies [62−66]. On the other hand, the transpot model has been successfully applied to describe collective phenomena in small collision systems, including charged-particle elliptic flow ($ v_2 $), triangular flow ($ v_3 $) [67], and flavor-dependent $ \it{p}_{\mathrm{T}} $-differential flow [68−73]. Building on these successful applications, we present the first systematic study of the $ \it{p}_\mathrm{T} $- and η-dependent flow vector decorrelation in p–Pb collisions using the AMPT (A Multi-Phase Transport) model.

The paper is organized as follows. In section II, a brief introduction about the AMPT and its various configurations is given. Section III introduces the observables to characterize the flow vector decorrelation as a funcyion of the $ \it{p}_{\mathrm{T}} $ and η, respectively. The two-particle correlation method and the advanced nonflow subtraction strategy are also presented. The results and related discussions are in section IV. Finally, a summary of this work is presented in section V.

The string-melting version of AMPT model [74, 75] is employed in this work to study the flow vector decorrelation in p–Pb collisions at 5.02 TeV. The AMPT model consists four main stages: initial conditions, partonic scattering, hadronization, and hadronic rescattering. The heavy ion jet interaction generator (HIJING) [76] is incorporated in the model to generate the initial conditions, where minijet partons and soft-excited strings are produced and then converted to primordial hadrons based on Lund fragmentation. The strength of Lund fragmentation is controlled by two key parameter, Lund string parameters a and b, which are approximately related to the string tension by $ \kappa \propto \dfrac{1}{b(2+a)} $. With the string melting mechanism, primordial hadrons are converted into partons, which are determined by their flavor and spin structures. The subsequent parton interactions are treated with the Zhang’s parton cascade (ZPC) model [77]. Only elastic scattering between the partons is considered in the model, and the cross-section of two-body scattering is described by the following simplified equation:

where $ \alpha_{s} $ is the strong coupling and the μ is the Debye screening mass. Once the partons stop scattering, the nearest two or three quarks are combined into mesons or baryons using a quark coalescence model. The generated hadrons then enter the hadronic rescatterings process, which is described by an extended relativistic transport (ART) model [78] including both elastic and inelastic scatterings for baryon-baryon, baryon-meson, and meson-meson interactions. Finally hadronic scatterings are terminated at a cutoff time ($ t_{\mathrm{max}} $), when the observables of interest are stable; a default cutoff time of $ t_{\mathrm{max}}=30 $ $ \mathrm{fm}/c $ is used.

In order to separate the impact from different physical processes on the flow vector decorrelation, we varied the key parameters of the model in the calculations of the flow vector. The effect of the partonic phase is investigated by varying the partonic scattering cross section σ from 0 mb and 0.5 mb to 3 mb. A smaller cross section corresponds to higher shear viscosity to entropy density ratio ($ \eta/s $) in viscous hydrodynamics in the AMPT model, and 0 mb of the cross section represents the exclusion of the parton scattering effect. Following the previous studies about the elliptic flow in p–Pb collisions [70−72], the default settings of Lund string parameters are $ a=0.3 $ and $ b=0.15 $. In this work, we further studied the initial conditions by varying $ a=0.5 $ and $ b=0.9 $, corresponding to a smaller string tension, when the partonic scattering cross section σ is set to 0.5 mb. In addition, the cutoff time $ t_{\mathrm{max}} $ is set to 0.6 fm/$ \it{c} $ to turn off the hadronic rescatterings, while the resonance decays are still included. We also analyzed the hadrons obtained right after the quark coalescence in the AMPT evolution (i.e. $ t_{\mathrm{max}} = 0 $ fm/$ \it{c} $), where both hadronic rescatterings and resonance decays are disabled. All configurations are summarized in the Table 1.

	Lund a	Lund b	Partonic cross section (mb)	$ t_{\mathrm{max}} $ fm/$ \it{c} $
Par1	0.3	0.15	0.5	30
Par2	0.3	0.15	3	30
Par3	0.3	0.15	0	30
Par4	0.5	0.9	0.5	30
Par5	0.3	0.15	0.5	0
Par6	0.3	0.15	0.5	0.6

Table 1.  Table of different configurations of AMPT parameters used in this work

The flow vector decorrelation is studied using the two-particle correlation method, which was widely applied in previous $ v_{2} $ measurements in p–Pb collisions [52, 79]. To simplify, the azimuthal correlation between two emission particles can be represented by $ N^{\mathrm{pair}} $ particle pairs as a function of the relative azimuthal angle $ \Delta\varphi = \varphi_{a} - \varphi_{b} $ between particles a and b and expanded in the Fourier series as follows:

where $ V_{n\Delta} $ refers to the two-particle n-th order harmonic. The tradition approach to calculate the $ \it{p}_{\mathrm{T}} $-differential flow of particle a (i.e. the particle of interest, POIs) is to firstly determine the flow coefficient of reference particles (RPs, labeld as "ref") over a wide kinematic range, called reference flow, and then the flow coefficient from $ \it{p}_{\mathrm{T}}^{a} $ interval can be expressed as:

where $ V_{n\Delta}(p_{\mathrm{T}}^{a},\mathrm{ref}) $ and $ V_{n\Delta}(\mathrm{ref},\mathrm{ref}) $ are obtained by construting the two particle correlation function $ C(\Delta\varphi) $ as Eq. 3 between the POIs and RPs, and the RPs, respectively. The $ \mathrm{\Psi}_{n}(p_{\mathrm{T}}^{a}) $ represents the $ p_{\mathrm{T}} $-differential symmetry plane angles at a specific $ p_{\mathrm{T}} $ range, which might fluctuate around the reference symmetry plane angles $ \mathrm{\Psi}_{n} $. The effect of the difference between $ \mathrm{\Psi}_{n}(p_{\mathrm{T}}^{a}) $ and $ \mathrm{\Psi}_{n} $ is quantified by the cosine term $ \mathrm{cos}[n(\Psi_{n}(p_{\mathrm{T}}^{a})-\Psi_{n})] $, which is called $ \it{p}_{\mathrm{T}} $-dependent flow angle fluctuations. On the other hand, the fluctuations of the flow magnitude are observed when the factorization hypothesis is broken [43, 44], i.e. the $ \langle v_{n}(p_{\mathrm{T}}^{a}) v_{n}^{\mathrm{ref}} \rangle $ cannot be factorised into the product of $ \sqrt{\langle v_{n}(p_{\mathrm{T}}^{a})^2 \rangle} $ and $ \sqrt{\langle {v_{n}^{\mathrm{ref}}}^2 \rangle} $. Another $ \it{p}_{\mathrm{T}} $ differential flow observable, denoted as $ v_{n}[2](p_{\mathrm{T}}^{2}) $, was proposed in [80], which is not affected by fluctuations in the flow angle or flow magnitude:

The ratio of $ v_{n}\{2\}(p_{\mathrm{T}}^{a}) $ and $ v_{n}[2](p_{\mathrm{T}}^{a}) $ is proposed to probe the $ p_{\mathrm{T}} $-dependent flow vector fluctuations:

One can see that if the $ p_{\mathrm{T}} $-dependent flow vector fluctuations present, the ratio value is smaller than unity. Similarly, another observable to probe the $ p_{\mathrm{T}} $-differential factorization ratio $ r_n $ was proposed in [80, 81],

The $ r_{n} < $ 1 indicates the breaking of factorization, suggesting the presence of $ p_{\mathrm{T}} $-dependent flow vector fluctuations.

Similarly, the η-dependent flow harmonics $ V_{n\Delta}(\eta^{a},\eta^{b}) $ are calculated by constructing two-particle correlations between pseudorapidity bins $ \eta^{a} $ and $ \eta^{b} $, following the same method as Eq. 3 but replacing $ p_{T}^{\mathrm{a}} $ and $ p_{T}^{\mathrm{b}} $ with $ \eta^{a} $ and $ \eta^{b} $. In order to investigate the longitudinal fluctuations of the flow vector, the decorrelation ratio $ r_n(\eta^{a},\eta^{b}) $ was proposed in Ref. [42], which is defined as:

where the $ \mathrm{cos}[n(\Psi_{n}(\eta^{a})-\Psi_{n}(\eta^{b}))] $ represents the impact of the variation in symmetry plane angles between the $ \eta^{a} $ and $ \eta^{b} $ bins, resulting from the η-dependent flow angle fluctuations. In addition, the flow magnitude decorrelation introduces additional η-dependent fluctuations, lead to the break of factorization of flow coefficient products: $ \langle v_{n}(-\eta^{a})v_{n}(\eta^{b}) \rangle \neq \sqrt{\langle v_{n}^{2}(-\eta^{a}) \rangle}\sqrt{\langle v_{n}^{2}(\eta^{b}) \rangle} $. For symmetric collision systems like Pb–Pb collisions, the $ v_{n} $ obtained from symmetric positive $ [v_n(\eta_a)] $ and negative $ [v_n(-\eta_a)] $ η regions are identical after averaging over all events. Therefore, the $ r_n(\eta^{a},\eta^{b}) $ is expected to converge to unity if neither flow magniture nor flow angle fluctuate along the longitudinal direction. If either of these effects, or both, are present, the $ r_n(\eta^{a},\eta^{b}) $ will be less than unity [50]. However, in an asymmetric collision system, such as p–Pb collisions, $ v_n(\eta_a) $ and $ v_n(-\eta_a) $ are generally not identical. As a result, it is not possible to isolate the η-dependent effects of symmetry-plane fluctuations in Eq. 8. The CMS collaboration proposed a method [42] to take the product of $ r_n(\eta^{a},\eta^{b}) $ and $ r_n(-\eta^{a},-\eta^{b}) $:

In this case, the $ v_{n} $ terms can be canceled in if there is no flow vector magnitude fluctuations, then the η-dependent flow vector decorrelation in p–Pb collisions can also be studied.

In small collision systems, the main contributions of the nonflow is from the jets, including both the short-range and long-range (also called "recoil") jet correlations [82]. The former can be effectively removed by introducing a large rapidity gap between the trigger and associated particles during the construction of the correlations, and the latter can be suppressed by many methods in the measurements based on the different assumptions. In this work, the template fit method developed by the ATLAS collaboration [60] is applied, which has been proven effective for nonflow subtraction in our previous studies [70] in the AMPT. For the given $ \it{p}_{\mathrm{T}} $ and η integral, the correlation function distribution obtained in high-multiplicity events is assumed to result from the superposition of the distribution obtained in low-multiplicity events scaled up by a multiplicative factor F and a constant modulated by $ \mathrm{cos}(n\Delta\varphi) $ for $ n > 1 $, as shown in

where G denotes the normalization factor, and $ V_{n\Delta} $ is the two-particle n-th order harmonic after the nonflow subtraction. The $ C^{\mathrm{LM}} $ is the correlation distributions obtained from the low-multiplicity events, and in this work the collisions with 60–100% centrality are selected. According to replacing Eq. 3 with Eq. 10, the flow vector fluctuations after the long-range nonflow subtraction can be calculated.

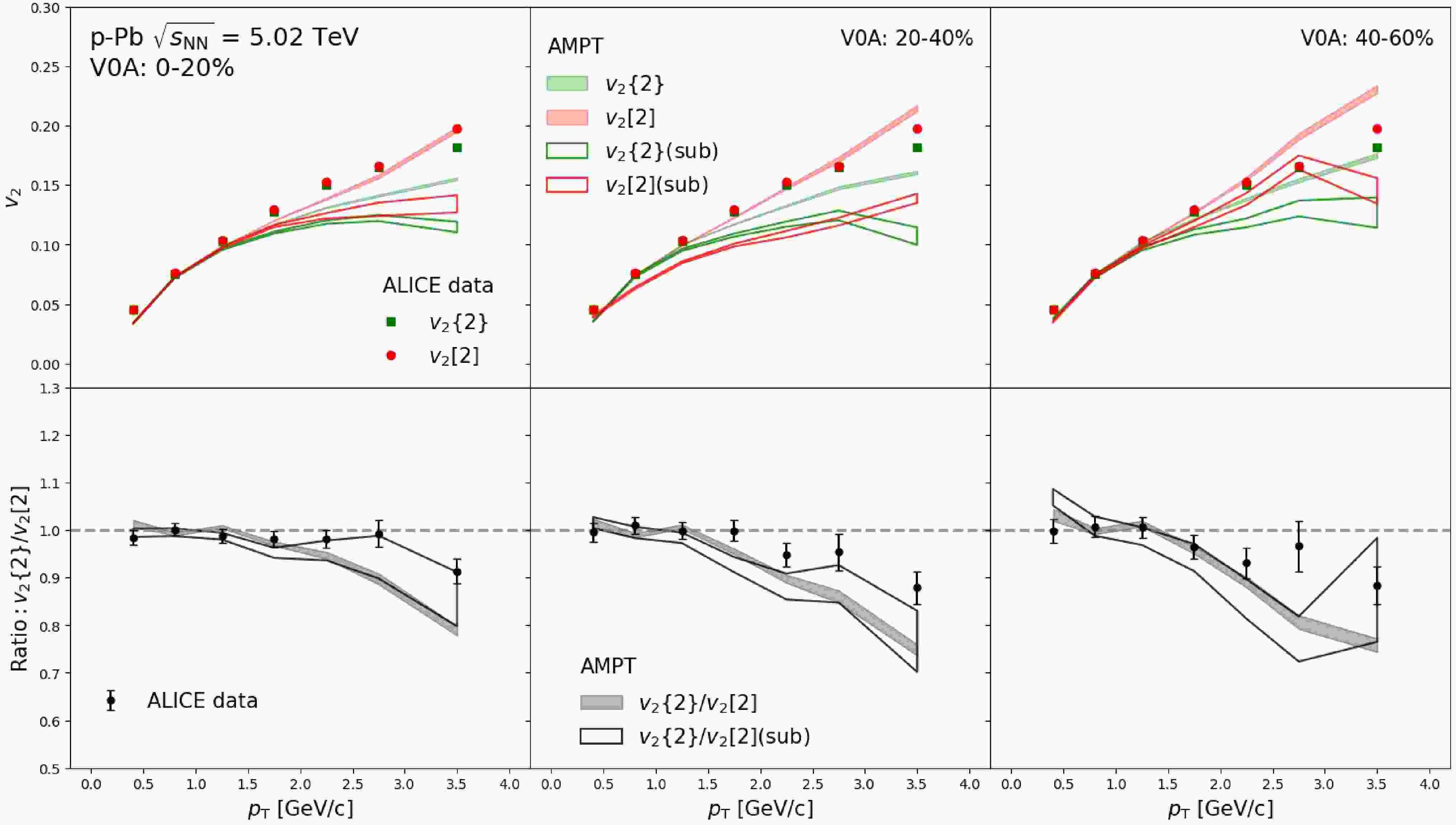
We first examine the $ p_{\mathrm{T}} $-differential $ v_{2} $ of charged hadrons in the pseudorapidity region $ |\eta|< $ 0.8 using the AMPT model with the default configuration (Par1) as described in Table 1. The $ v_{2}\{2\} $ and $ v_{2}[2] $ are calculated according to Eq. 4 and Eq. 5. Figure 1 shows the $ p_{\mathrm{T}} $-differential $ v_{2}\{2\} $ and $ v_{2}[2\} $ for 0–20%, 20–40%, and 40–60% centrality bins obtained from the AMPT calculations, compared with ALICE measurements [41]. To suppress contributions from short-range jet correlations, the $ |\Delta\eta| > 0.8 $ is applied. The calculations reasonably reproduce the $ v_{2} $ data from central to semi-central collisions, and the ratio $ v_{2}\{2\}/v_{2}[2\} $ shows deviations from unity above $ \it{p}_{\mathrm{T}} \simeq $ 2 GeV/c. These deviations increase with $ \it{p}_{\mathrm{T}} $, similar to findings in Pb–Pb collisions, indicating $ p_{\mathrm{T}} $-dependent flow vector fluctuations in p–Pb collisions from the AMPT model. Unlike Pb–Pb collisions, these deviations do not significantly depend on centrality selections. To determine if these deviations are caused by non-flow effects from long-range jet correlations, we apply the template fit subtraction method described in Eq. 10. As expected, the $ v_{2} $ after subtraction, shown in Fig. 1 (dashed line), is lower than the results without subtraction, especially at high $ p_{\mathrm{T}} > $ 2 GeV/c. The ratio $ v_{2}\{2\}/v_{2}[2\} $ after subtraction is consistent with that before subtraction within uncertainties. This indicates that the long-range jet contribution to the decorrelations is negligible here, and the observed $ p_{\mathrm{T}} $-dependent flow vector fluctuations in p–Pb collisions are mainly from real flow signals.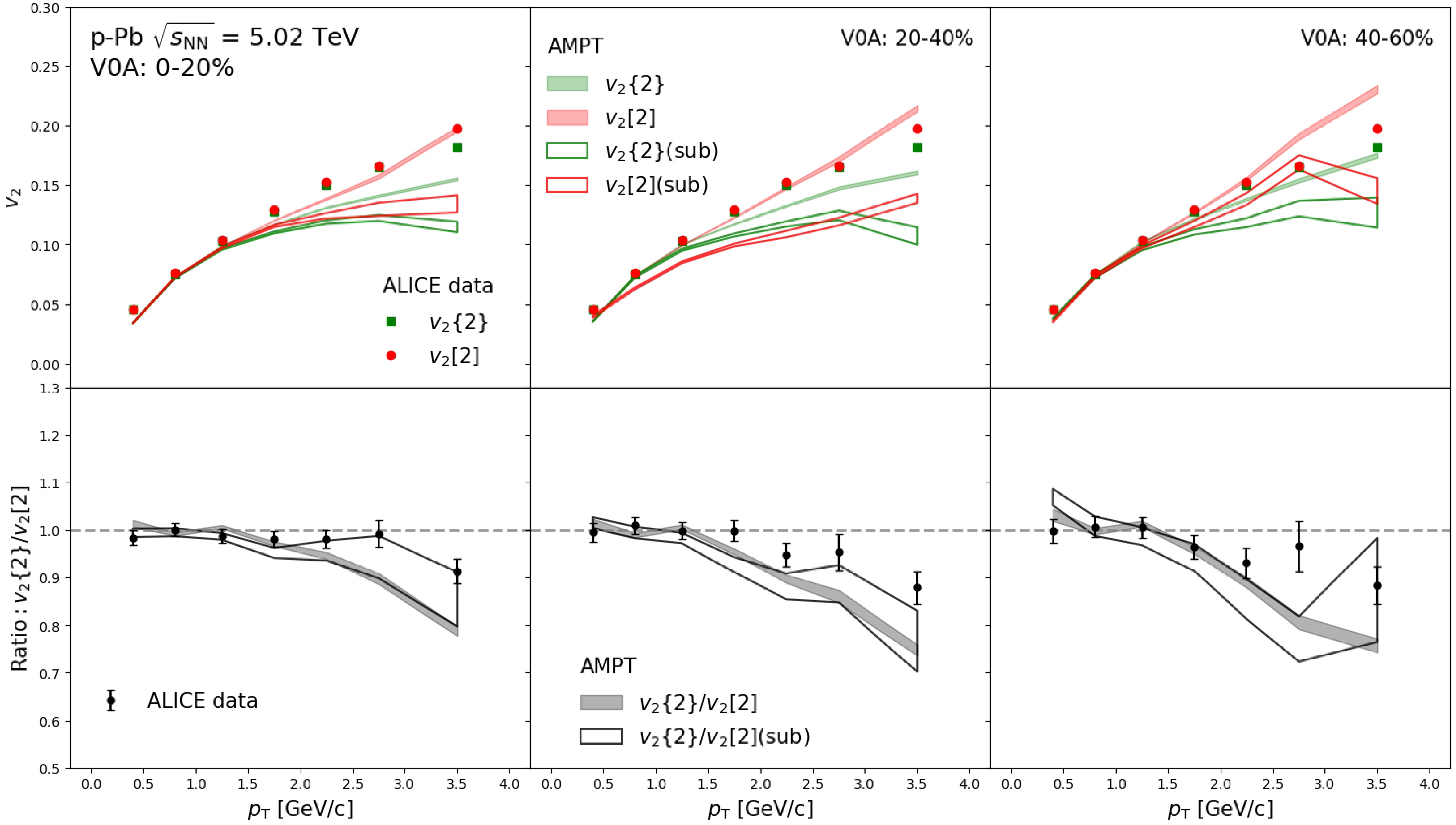

Figure 1.  (Color online) The $ v_{2}\{2\}$ and $ v_{2}[2]$ as a function of $p_{\mathrm{T}} $ and their ratio obtained from the AMPT model in 0–20%, 20–40% and 40–60% p–Pb collisions at 5.02 TeV, in comparison of the ALICE measurements [41]. The results with the nonflow subtraction obtained from the AMPT model are also shown.

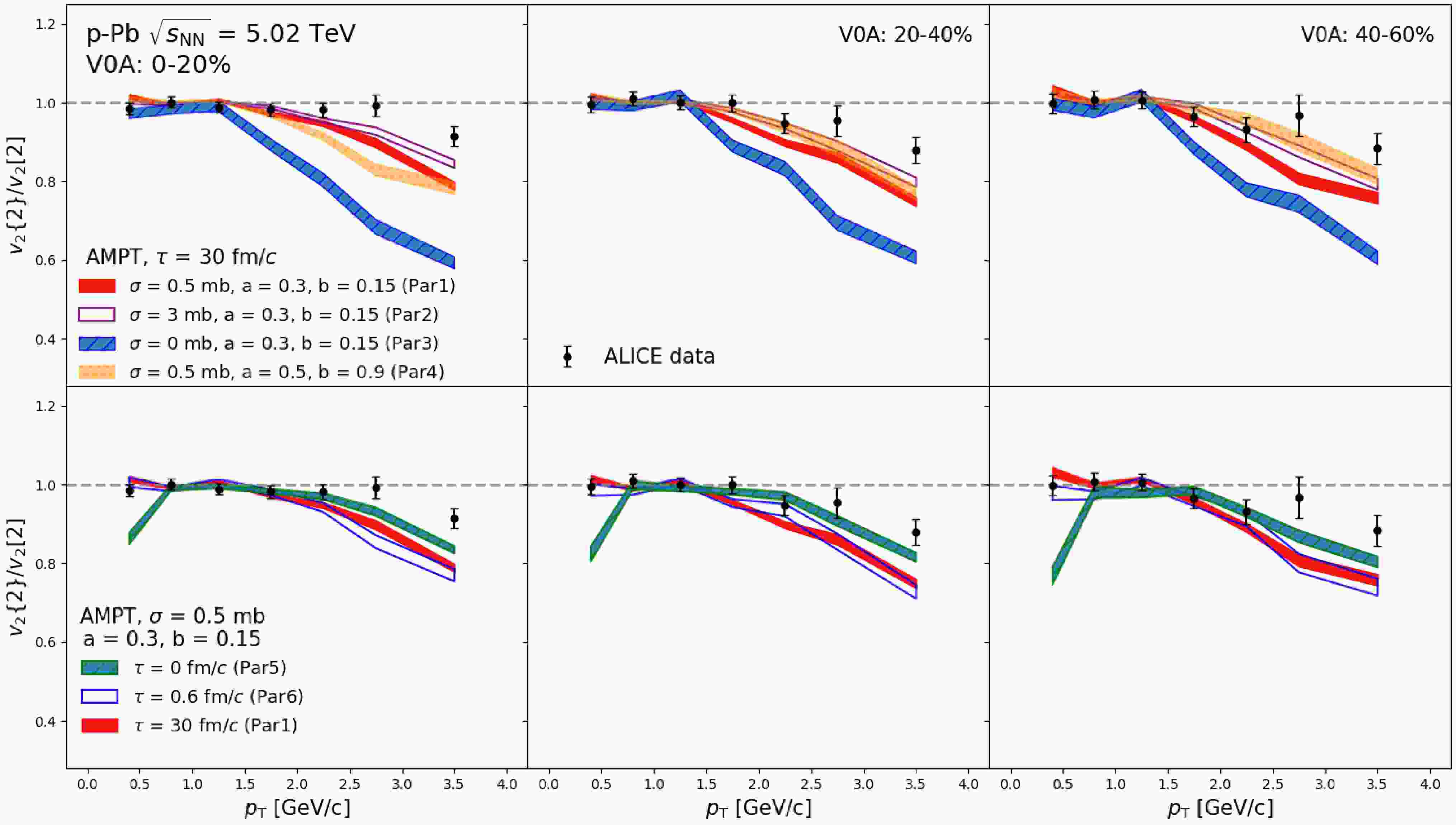
Figure 2 shows the $ p_{\mathrm{T}} $-dependent $ v_{2}\{2\}/v_{2}[2\} $ ratio in 0–20%, 20–40%, and 40–60% centrality classes obtained from the AMPT model with different configurations, compared to the ALICE data points [41]. For direct comparison with the data, nonflow subtraction is not applied here. The impact of the partonic scattering on the ratio can be seen by comparing the results from Par1, Par2, and Par3, as shown in Fig. 2 (top). The ratio obtained from larger parton scattering cross section (Par2) is slightly higher than the results from Par1. On the other hand, a large deviation to unity is observed when the cross section is set to $ \sigma=0 $ mb (Par3). It may attribute to the break of factorization from the nonflow, since the parton scattering process was proved to be the main contribution to the flow in small collision systems [70]. The effect from varying the initial conditions via the Lund string parameters, a and b, can be seen by comparing the results from Par4 and Par1, as shown in Fig. 2 (top). One can see that the $ v_{2}\{2\} $/$ v_{2}[2] $ ratio obtained with larger Lund a and b (Par4) is lower in the most 0–20% collisions. With the increaing of the centralities, the resuts from Par4 are enhanced, and finally are hihger than the results from Par1. The effects from the hadronic scatterings are studied by varying the cutoff time of hadronic rescatterings, which can seen in the comparison of the results of Par1, Par5 and Par6, as shown in Fig. 2 (bottom). The $ v_{2}\{2\} $/$ v_{2}[2] $ ratio from Par1 and Par6 are consistent within uncertainties from the central to peripheral collisions, indicating that the impact from hadronic scatterings on the flow vector fluctuations are negligible. It is consistent with the previous findings that the hadronic scatterings have almost no effects on the $ p_{\mathrm{T}} $-differential $ v_{2} $ in p–Pb collisions [70]. For the case of Par5, where both the resonance decay and the hadronic scatterings are turn off, the $ v_{2}\{2\} $/$ v_{2}[2] $ ratio is lower at $ p_{\mathrm{T}}<0.8 $ GeV/c but higher at $ p_{\mathrm{T}}>1.4 $ GeV/c compare to the results of Par1 and Par6. It is expected since the decay processes convert high-$ p_{\mathrm{T}} $ hadrons into low-$ p_{\mathrm{T}} $ particles, thereby shifting the overall ratio toward the low-$ p_{\mathrm{T}} $ region. One can see that the results of all configurations underestimate the data, suggesting that the model needs further tuning.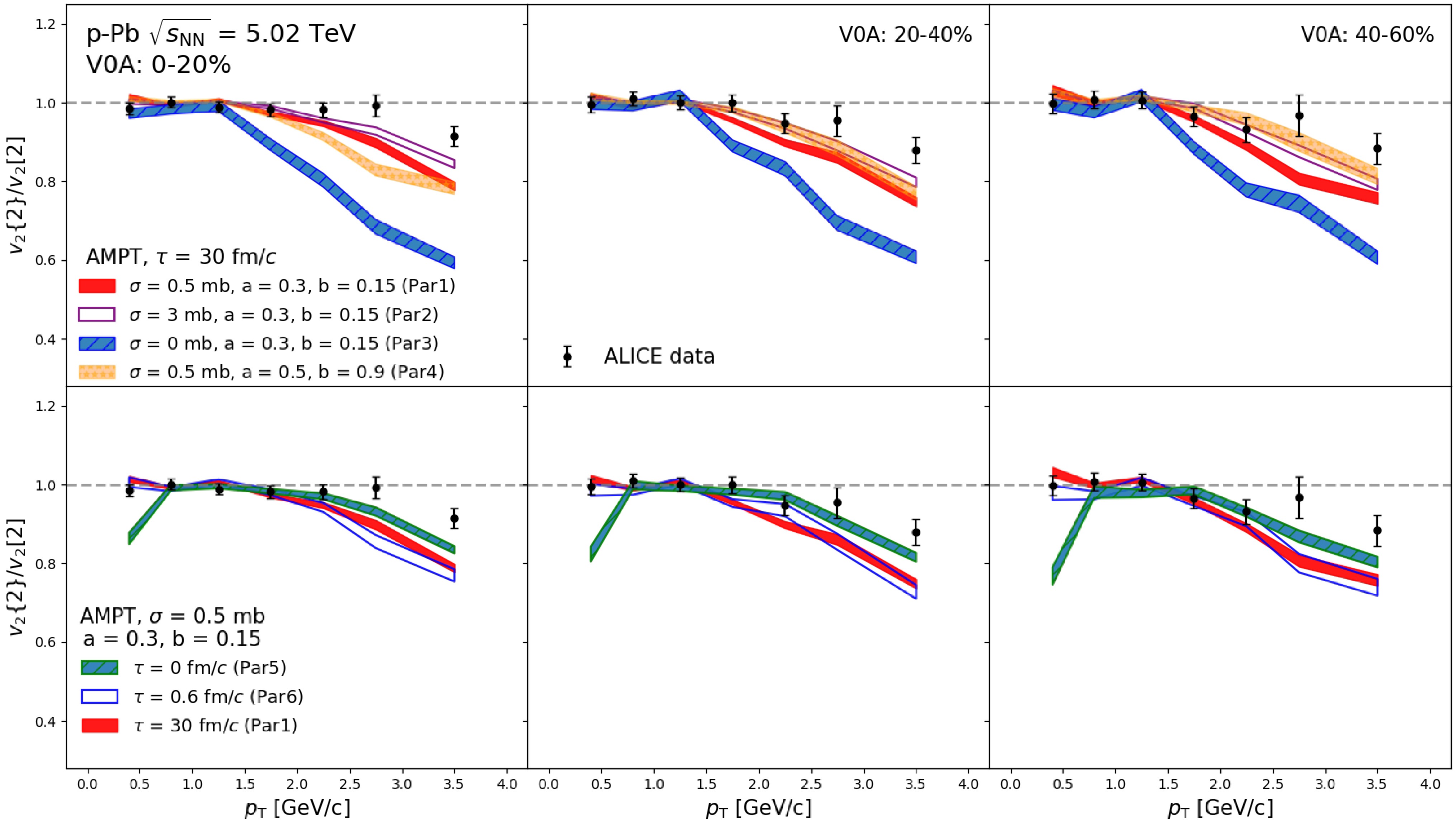

Figure 2.  (Color online) The $p_{\mathrm{T}}$-dependent $v_{2}\{2\}$/$v_{2}[2]$ ratio in 0–20%, 20–40%, 40–60% centrality classes from the AMPT model with different configurations. ALICE data points [41] are shown as black open circles for comparison.

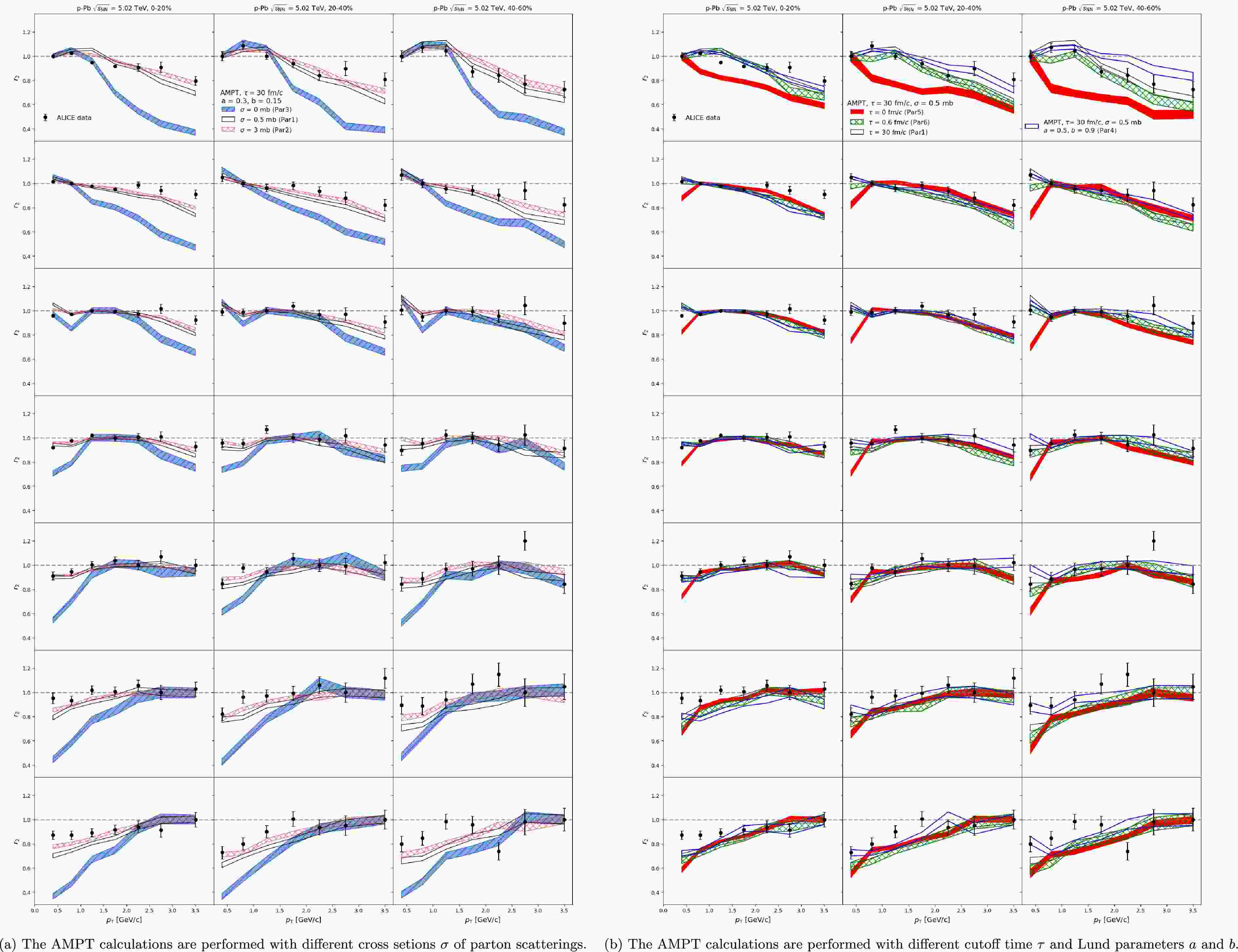
The factorization ratio $ r_{2} $, definded in Eq. 7, is calculated in different centrality and $ p^{b}_{\mathrm{T}} $ ranges, and compared to the ALICE data points [41] in Fig. 3. The results from the AMPT model with different configurations are shown in Fig. 3a (Par1, Par2 vs, Par3) and Fig. 3b (Par1, Par4, Par5, Par6). Simlar to the Fig. 2, nonflow subtraction is not applied here. The model with a 0.5 mb cross section, a = 0.3, b = 0.15 and τ = 30 fm/c (Par1), provides a fair description of the data in all centrality and $ p_{\mathrm{T}} $ bins. The deviation of the $ r_{2} $ from the unity has no dependence on the centrality selections, and is more pronounced with the increasing $ |p^{a}_{\mathrm{T}}-p^{b}_{\mathrm{T}}| $. The $ r_{2} $ obtained with larger Lund a and b (Par4) are higher in more peripheral collisions, reflecting the effects from the initial conditions. Changing the partonic scattering cross section from 0.5 mb to 3 mb (Par1 vs Par3) slightly enhance the $ r_{2} $, while the results obtained with $ \sigma=0 $ mb shows a significant breakdown of the factorization at large $ |p^{a}_{\mathrm{T}}-p^{b}_{\mathrm{T}}| $. The impacts from the hadronic scatterings are negligible for all centralities and $ p_{\mathrm{T}} $ bins (Par1 vs Par6), but the resonance decay process still has large impacts on the $ r_{2} $ at low-$ p_{\mathrm{T}} $ region (Par1 vs Par5). One can see that the calculations of $ r_{2} $ and $ v_{2}\{2\} $/$ v_{2}[2] $ ratio have generally similar dependence on the initial conditions, parton scattering cross section, hadron scattering process. It is expected since $ r_{2} $ is basically the double-differential $ v_{2}\{2\} $/$ v_{2}[2] $ ratio [59].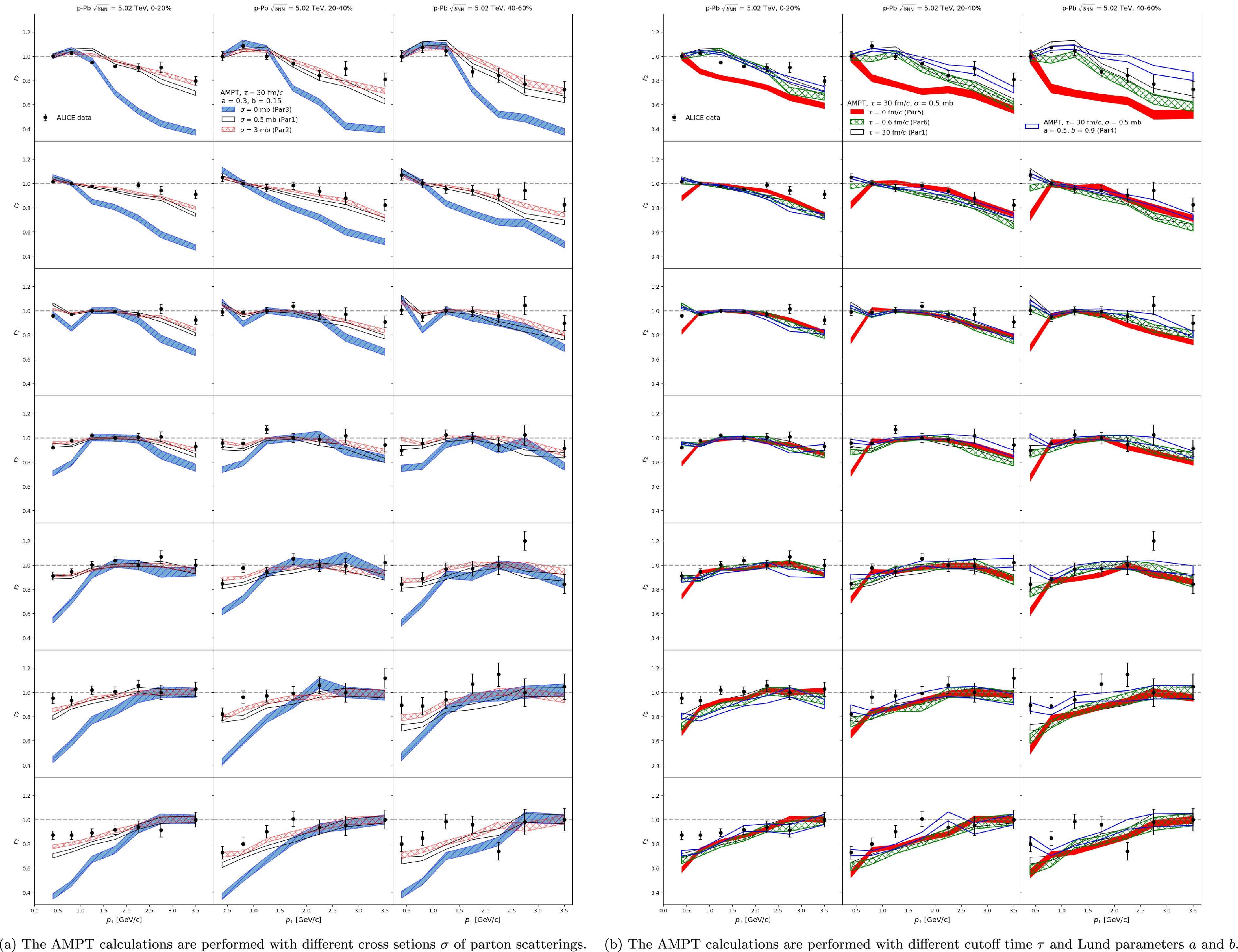

Figure 3.  (Color online) The factorization ratio $ r_2 $ as a function of $ p^{a}_{\mathrm{T}} $ obtained from the AMPT calculations, in different centrality and $ p^{b}_{\mathrm{T}} $ ranges, is compared to the ALICE data points [41].

The η-dependent $ v_{2} $ is first calculated before studying the decorrelation. We follow the two-particle correlation method and the nonflow subtraction strategy used by the ALICE experiment [54]. The correlation between three groups of particles is constructed based on Eq. 10, then the flow coefficients are extracted for three combinations:

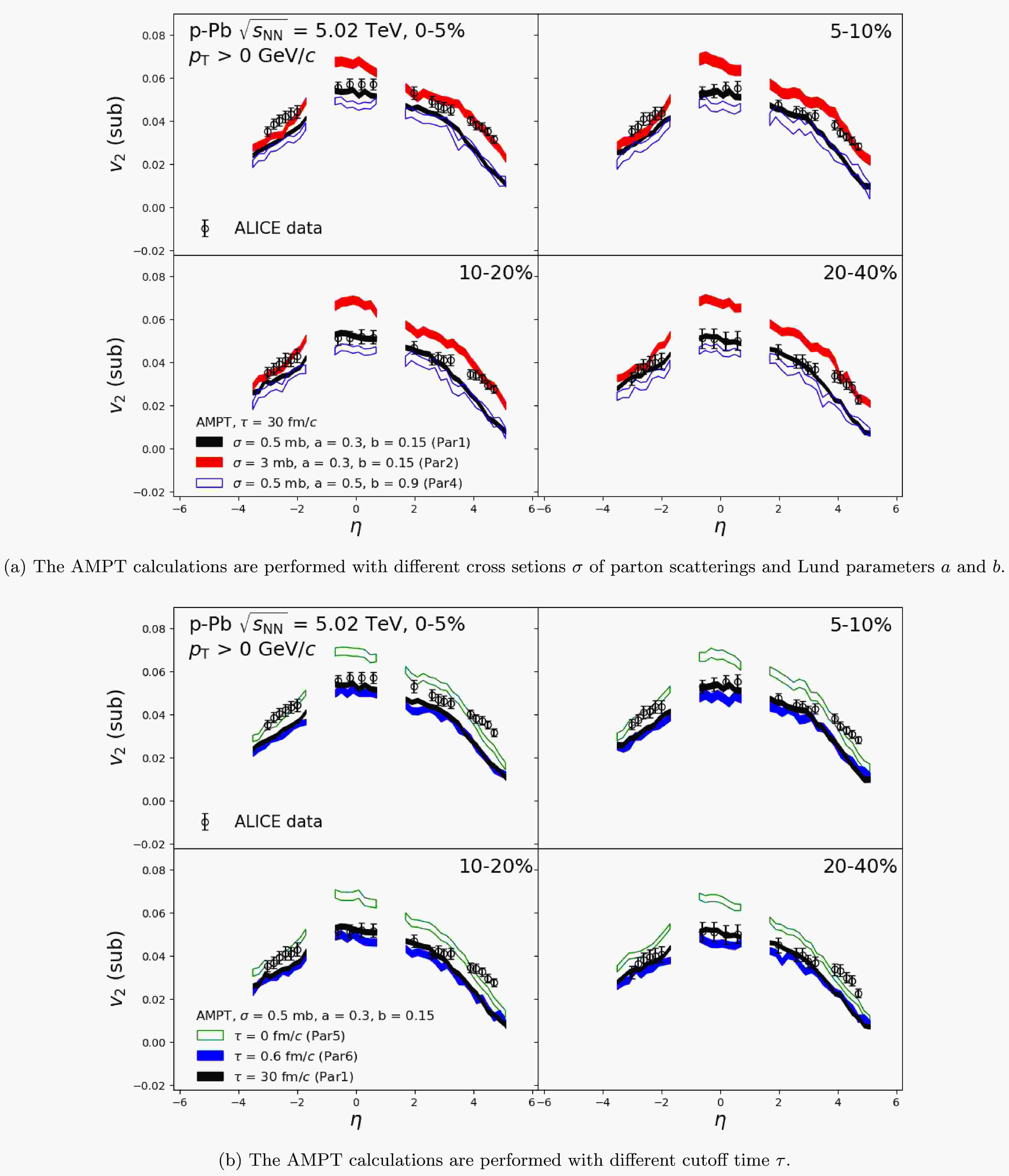
where a, b, and c represent the hadrons with $ p_{\mathrm{T}}> $ 0 GeV/c at different rapidity bins. Similarly, $ v_{n}(\eta^{a}) $ and $ v_{n}(\eta^{b}) $ can be obtained by alternating the indices a, b, and c in Eq. 11. Figure 4 shows the $ v_{2} $ of the charged hadrons for $ p_{\mathrm{T}}> $ 0 GeV/c as a function of η in 0–5%, 5–10%, 10–20%, and 20–40% centrality ranges, and the comparison to the ALICE data [54]. The results obtained from different configurations of the AMPT model are shown in Fig. 4a and Fig. 4b, respectively. The calculations obtained with a 0.5 mb cross section, a = 0.3, b = 0.15, and τ = 30 fm/c (Par1) provide a good description of the data at mid-rapidity but slightly underestimate the $ v_{2} $ at forward and backward rapidity. On the other hand, the Par2 calculations with a larger cross section (σ = 3 mb) describe the data at forward and backward rapidity but significantly overestimate the $ v_{2} $ at mid-rapidity. The calculations without hadron rescatterings (Par6) are lower compared to the Par1 results, especially at mid-rapidity, while the deviation is negligible at forward and backward rapidity. Similar behavior is observed in the results obtained with larger Lund a and b (Par4). Furthermore, the results obtained from Par5 are significantly enhanced for all rapidity bins, indicating the impact of resonance decay on the integrated-$ v_{2} $. One can see that the results from all configurations cannot simultaneously describe the data at mid- and forward/backward-rapidity. This suggests that the rapidity dependence of parameters (e.g., the initial conditions, the strength of parton interactions) needs to be considered in further developments of the model [75].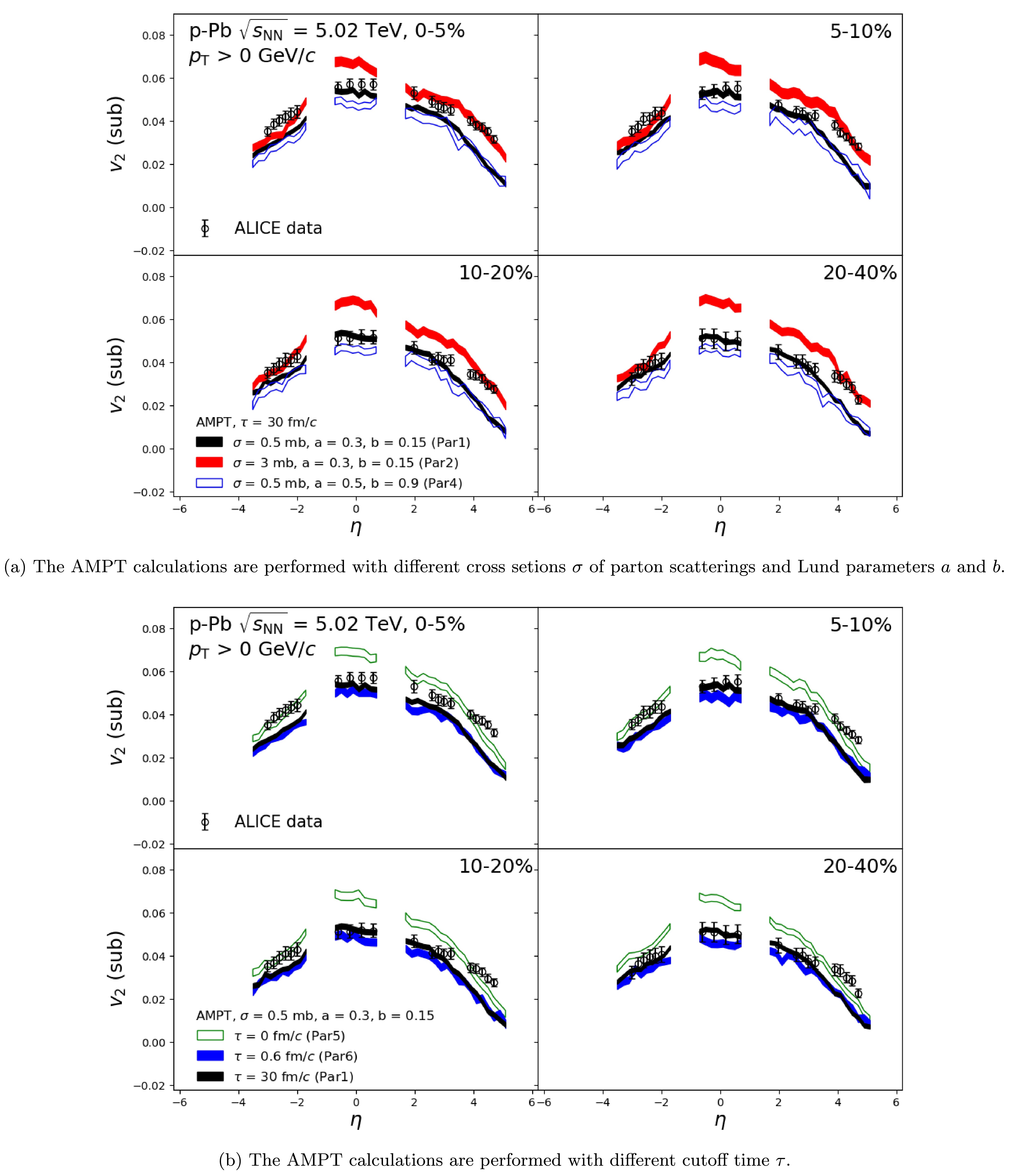

Figure 4.  (Color online) The $ v_{2} $ as a function of pseudorapidity η in in different centrality ranges, obtained from the AMPT model with various configurations. ALICE data points [54] are shown as black open circles for comparison.

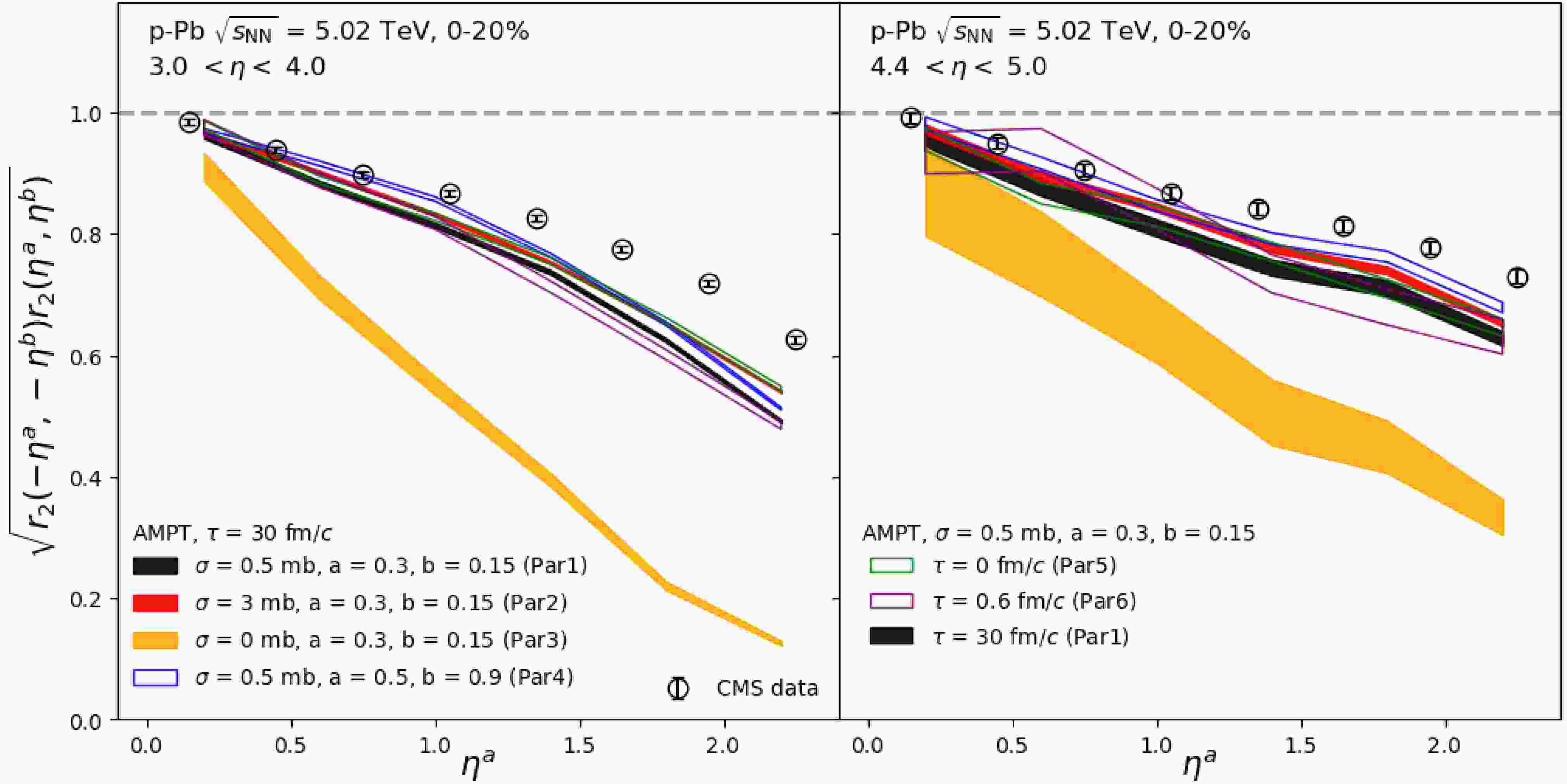
As defined in Eq. 9, the η-dependent $ \sqrt{r_{2}(\eta^{a},\eta^{b})r_{2}(-\eta^{a},-\eta^{b})} $ in p–Pb collisions at 5.02 TeV for 3 $ < \eta^{b} < $ 4 and $ 4.4 < \eta^{b} < 5.0 $ are shown in Fig. 5. The results obtained from the AMPT with all configurations are compared to the measurements from the CMS collaboration [42]. In order to compare with the data directly, we don't apply the nonflow subtraction here. All calculations show a larger breakdown of factorization as $ \eta^{a} $ increases, as observed in data. Similar to the findings in the $ p_{\mathrm{T}} $-dependent flow vector decorrelation, a significant breakdown of factorization is observed when the parton scattering cross section is set to 0 (Par3), but the difference between the results of cross section $ \sigma=0.5 $ mb (Par1) and $ \sigma=3 $ mb (Par2) is small. The decorrelations obtained without hadronic scatterings (Par6) are consistent with Par1 calculations, suggesting that η-dependent decorrelation has no sensitivity to the hadronic scatterings. No significant effect of the resonance decay is observed for $ \eta^{a} < $ 1, while a slight enhancement is shown for $ \eta^{a} > $ 1 (Par1 vs Par5). On the other hand, varying the Lund parameters to $ a=0.5 $, $ b=0.9 $ (Par4) leads to a smaller decorrelation for both 3 $ < \eta^{b} < $ 4 and 4.4 $ < \eta^{b} < $ 5 (Par4 vs Par1), reflecting the effects from initial conditions. In general, the model calculations with all tunings, except for $ \sigma=0 $, provide a fair description of the data for $ 4.4 < \eta^{b} < 5.0 $, but systematically overestimate the deviation from unity of decorrelations for 3 $ < \eta^{b} < $ 4 and $ \eta^{a}> $ 1.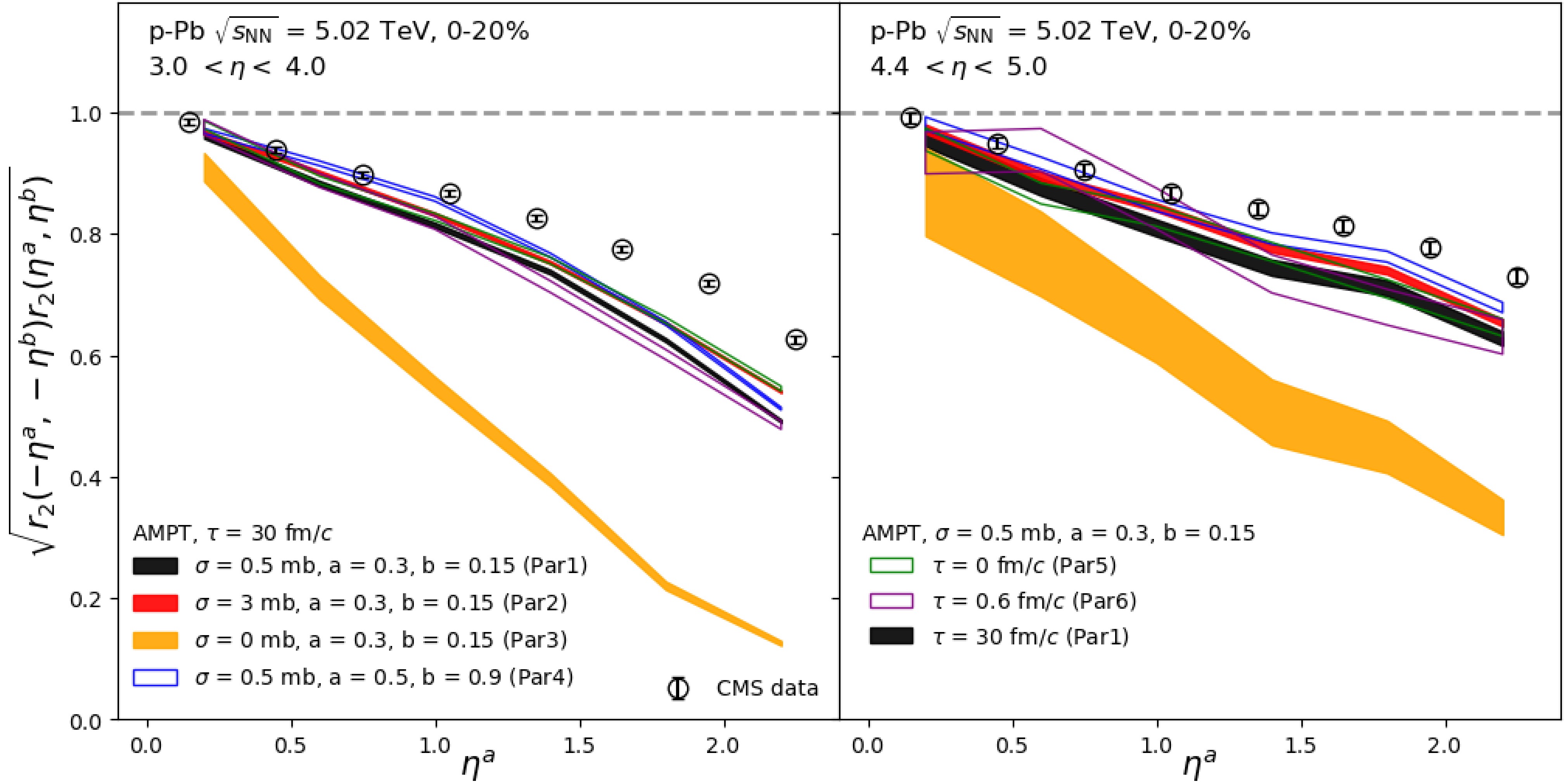

Figure 5.  (Color online) The square root of the product of factorization ratios, $\sqrt{r_{2}(\eta^{a},\eta^{b})r_{2}(-\eta^{a},-\eta^{b})}$, as a function of $\eta^{a}$ for 3.0 $< \eta^{b} <$ 4.0 (left) and $4.4 < \eta^{b} < 5.0$ (right), in 0–20% centrality class of p–Pb collisions at 5.02 TeV, obtained from the AMPT model with various tunings. The CMS data points [42] are shown as black open circles for comparison.

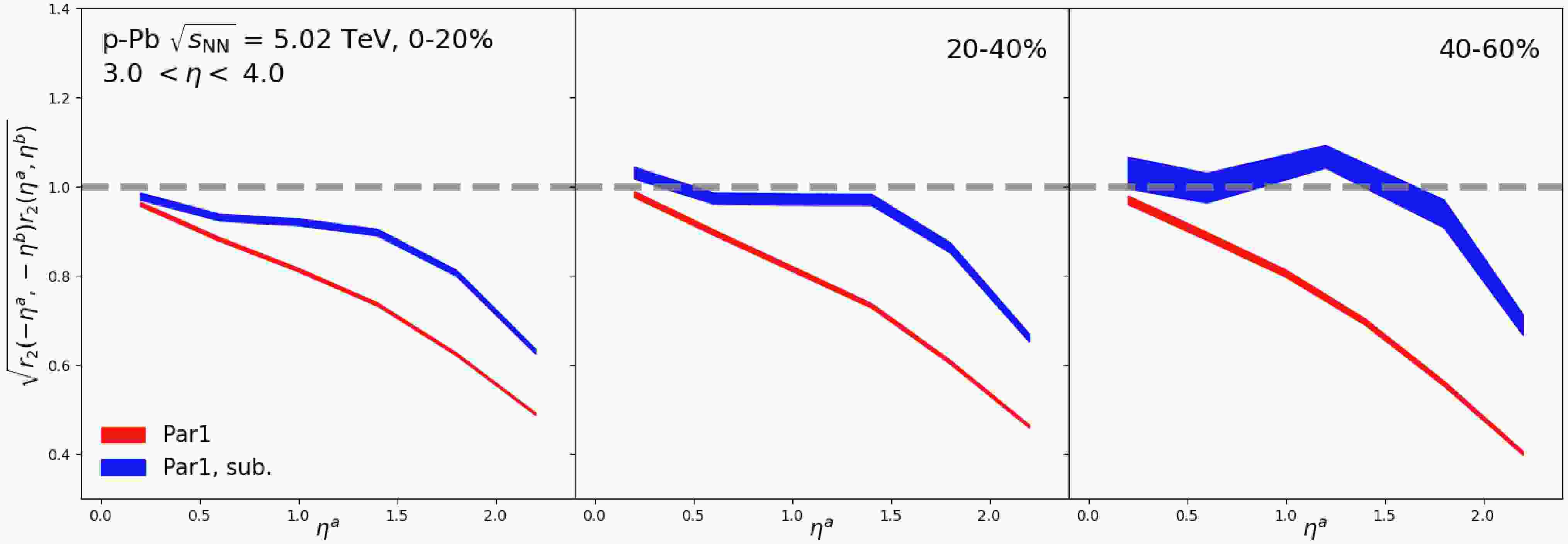
Figure 6 shows the $ \sqrt{r_{2}(\eta^{a},\eta^{b})r_{2}(-\eta^{a},-\eta^{b})} $ as a function of $ \eta^{a} $ in 0–20%, 20–40% and 40–60% centrality classes before and after the nonflow subtraction. The template fit method described in Eq. 10 is applied for the calculations of Eq. 8 and Eq. 9, where the contribution from the long-range jet correlations is suppressed. After subtraction, the decorrelation decreases significantly across all three centrality classes, approaching unity. This indicates that the η-dependent flow vector decorrelation in p–Pb collisions is strongly influenced by nonflow effects (e.g., dijets). This is consistent with the findings in recent measurements in smaller pp collisions performed by the ATLAS collaboration [57]. On the other hand, the difference between the results before and after the nonflow subtraction becomes larger with the increasing centrality. Especially in the 40–60% centrality class, the tendency of the decorrelation completely changes after the nonflow subtraction, first increasing then decreasing with the increasing $ \eta^{a} $. It is worth noting that such an effect from the long-range jet correlations is negligible for the $ p_{\mathrm{T}} $-dependent decorrelation at mid-rapidity ($ |\eta|< $0.8), as shown in Fig. 1. This is because the contribution from long-range jet correlations to the $ v_2 $ is more significant at forward/backward rapidity compared to mid-rapidity in small collision systems [83]. This hints at the important role of the subtraction of long-range jet correlations in the calculations of longitudinal fluctuations of the flow vector in the small collision systems. More measurements of the flow vector decorrelation in p–Pb collisions with a proper long-range jet contribution subtration are needed in the future.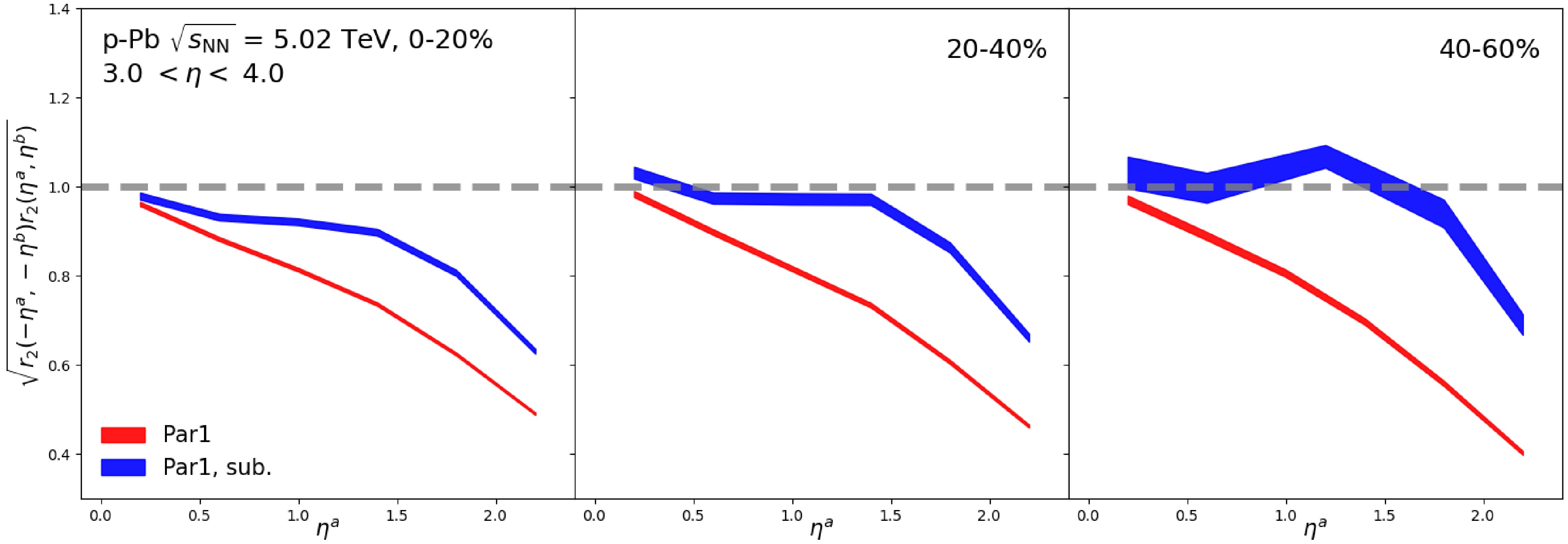

Figure 6.  (Color online) The comparison of the $\sqrt{r_{2}(\eta^{a},\eta^{b})r_{2}(-\eta^{a},-\eta^{b})}$, as a function of $\eta^{a}$ for 3.0 $< \eta^{b} <$ 4.0, in p–Pb collisions at 5.02 TeV between before and after nonflow subtraction. The results in 0–20% (left), 20–40% (middle) and 40–60% (right) centrality classes are all shown.

The $ \mathrm{p}_{T} $- and η-dependent decorrelation of the flow vector in p–Pb collisions at $ \sqrt{s_{\mathrm{NN}}}= $ 5.02 TeV are systematically studied with the AMPT model in this paper. The sensitivity of the decorrelations to the initial conditions, the partonic scatterings, the haronic rescatterings are probed by varying the configurations of the model. It is found that the observables are driven by the partonic scatterings and the initial conditions together, but has weak dependence on the hadronic rescattering. It suggests that the event-by-event fluctuations of the initial state lead to the fluctuations of the flow vector observed in the final state through the parton interactions. These results point to the possibility for employing flow vector decorrelation to investigate the transport properties of the hot and dense medium likely formed in small collision systems. Furthermore, we demonstrate that long-range jet correlations significantly influence the longitudinal decorrelation in p–Pb collisions. It provides further insights in understanding the fluctuations of the flow vector in small collision systems and has referential value for future measurements.

The computation is completed in the HPC Platform of Wuhan Textile University.