Collective impact of higher order deformations of target nuclei on the fusion dynamics of heavy-ion induced reactions

The deviation of the nuclear shape from spherical symmetry due to multipole moments of different order gives rise to specific nuclear shapes with significant change in radius vectors [1−3]. Numerous attempts have been made to investigate the impact of these deformed nuclear shapes associated with the projectile and target nuclei on the dynamics of heavy-ion-induced fusion reactions [4−26]. 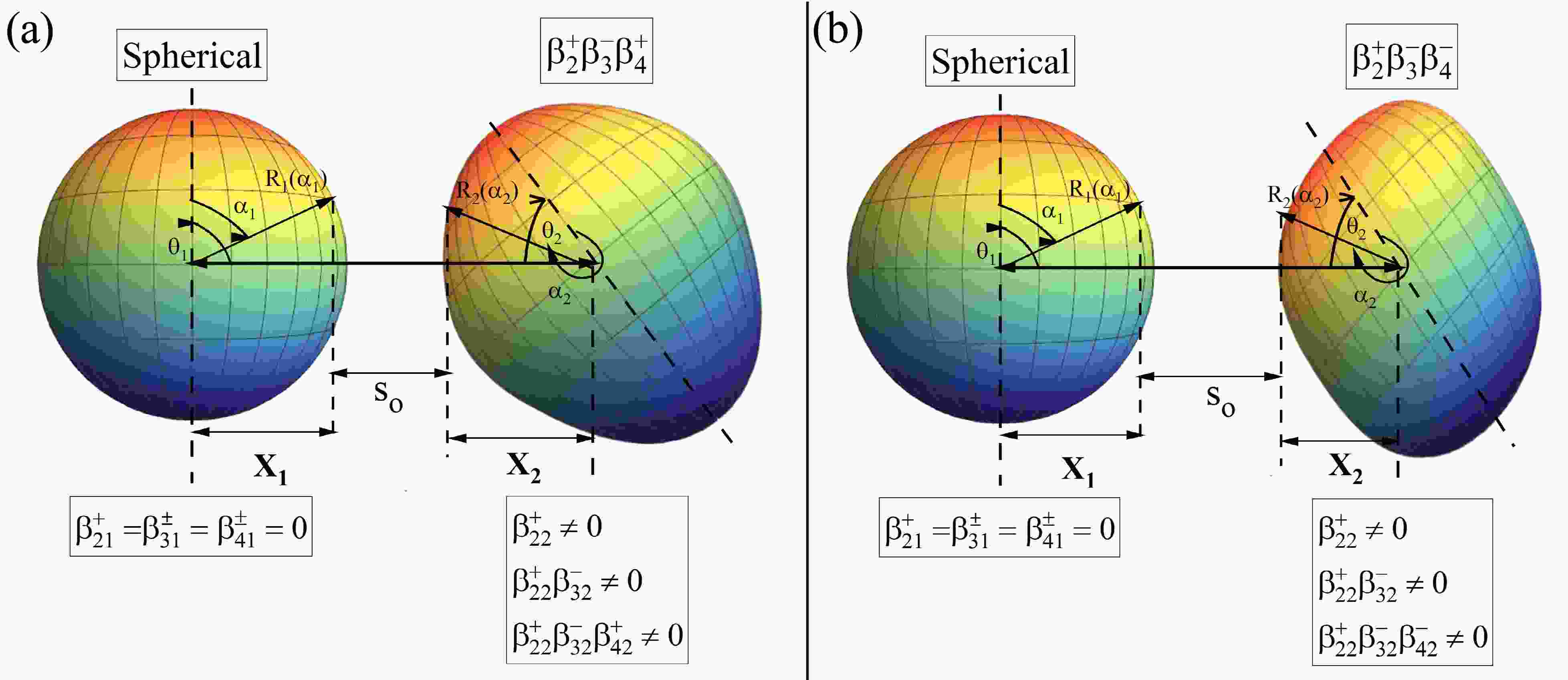Initially, it was believed that considering solely the quadrupole deformation ($ \beta_2 $) would suffice for investigating the dynamics of fusion reactions. Numerous scientists have investigated the impact of quadrupole deformation $ \beta_2 $ and have uncovered its significance alongside the orientation degree of freedom, in contrast to the spherical nuclei [27−36]. The study of orientation degree of freedom is performed by studying the compact (or elongated) configuration, otherwise also known as belly-to-belly (or pole-to-pole) configuration corresponding to the maximum (minimum) barrier height $ V_B $ and smallest (largest) interaction radius $ R_B $, respectively [30, 34, 37−39]. For instance, the elongated (pole-to-pole) configuration of prolate quadrupole ($ \beta_2^+ $) deformed nuclei lowers the fusion barrier and consequently enhances the reaction cross-sections. Conversely, quadrupole-deformed nuclei's compact (belly-to-belly) configuration raises the fusion barrier, thereby reducing the cross-section [40]. In other words, based on these configurations, researchers have explored the relevance of deformations and orientation degrees of freedom in heavy-ion-induced fusion reactions for incident beam energies lying across the Coulomb barrier. In Ref. [37, 41, 42], the authors also investigated the influence and significance of including the octupole deformation ($ \beta_3 $) alongside the quadrupole deformation ($ \beta_2 $) leading to the pear-shaped nuclei [43]. These pear-shaped nuclei are further categorized with respect to the magnitude of octupole ($ \beta_3 $) deformation compared to the magnitude of quadrupole $ \beta_2 $ deformation. While the nuclei possessing a higher magnitude of $ \beta_3 $ deformation as compared to that of $ \beta_2 $ deformation are called rigid pear deformed nuclei, the nuclei possessing a smaller magnitude of $ \beta_3 $ deformation as compared to that of $ \beta_2 $ deformation are termed as soft pear deformed nuclei. In these studies, it is demonstrated that the inclusion of higher-order deformations i.e., $ \beta_3 $ deformation in this case, significantly modifies the barrier characteristics as well as the optimum orientations and hence impacts the dynamics of the reactions and is, therefore, necessary to be taken into account [41, 42, 44]. Discrepancies existed in the viewpoints regarding the inclusion of the higher-order deformations up to hexadecapole deformation $ \beta_4 $, primarily due to an insufficient understanding of higher-order deformations. Nevertheless, numerous studies have explored the effects of hexadecapole deformation in nuclear reaction dynamics [46−54]. But the collective behavior and influence of quadrupole, octupole, and hexadecapole deformations in nuclei exhibiting all three types of deformation have not been explicitly studied. In our recent work, we thoroughly investigated the impact of hexadecapole-deformed nuclei on the fusion dynamics of heavy-ion-induced fusion reactions. Our findings reveal that the incorporation of hexadecapole deformation of the target nuclei leads to significant modifications in the characteristics of the fusion barrier $ V_B $ and $ R_B $, as well as the optimal orientation $ \theta_{opt} $ and consequently, the cross-sections of the fusion reactions. Furthermore, our observations also reveal that $ \beta_4 $ deformation of varying magnitudes and signs cause elongation and compression of nuclear shapes. These modifications in the nuclear shape have distinct effects on the barrier characteristics $ V_B $ and $ R_B $, ultimately influencing the dynamics of the reaction in specific manners [55, 56]. However, it is important to note we only explored the nuclei with axially symmetrical shapes and incorporated solely the $ \beta_2 $ and $ \beta_4 $ deformations for the coplanar systems. As shown in [55], our findings intrigued us to explore the collective effect of $ \beta_2 $, $ \beta_3 $ and $ \beta_4 $ deformations. Our investigation has uncovered that the inclusion of all deformations up to $ \beta_4 $ impart a greater influence on the barrier characteristics as compared to any other combination of deformations, such as $ \beta_2^{\pm}\beta_3^{\pm} $ or $ \beta_2^{\pm}\beta_4^{\pm} $.

The variation in nuclear shape as we incorporate deformations of varying orders can be seen in Fig. 1. The figure portrays the expansion and contraction along the belly region of nuclei, as well as the nuclear radius vector when deformations of all orders (up to $ \beta_4^{\pm} $) having different signs are included in conjunction with the quadrupole deformation ($ \beta_2^{\pm} $). The transition from spherical to ellipsoidal symmetry along the major/minor axis of the nuclei occurs according to the sign(±) of the associated quadrupole deformation $ \beta_2^+ $ and $ \beta_2^- $, respectively, resulting in prolate and oblate deformed nuclei. Incorporating $ \beta_3^{\pm} $ to these prolate and oblate deformed nuclei breaks the reflection symmetry and gives rise to pear-shaped deformed nuclei. Interestingly, the inclusion of $ \beta_4^+ $ results in expansion along the major/minor axis according to the sign of $ \beta_2 $ and $ \beta_3^{\pm} $, leading to the belly-out configuration of deformed nuclei. Similarly, incorporating $ \beta_4^- $ produces compression along the major/minor axis according to the sign of $ \beta_2 $ and $ \beta_3^{\pm} $, resulting in the belly-in configuration of deformed nuclei. This change in the nuclear shape and symmetry leads to a change in the respective radius vector of the deformed target nuclei, which further heavily affects the reaction dynamics. Fig. 1 also illustrates the configuration of the Spherical + $ \beta_2^+\beta_3^-\beta_4^{\pm} $ deformed nuclei, portraying the altered geometry and its impact on the shortest distance ($ s_o $), calculated between the colliding nuclei.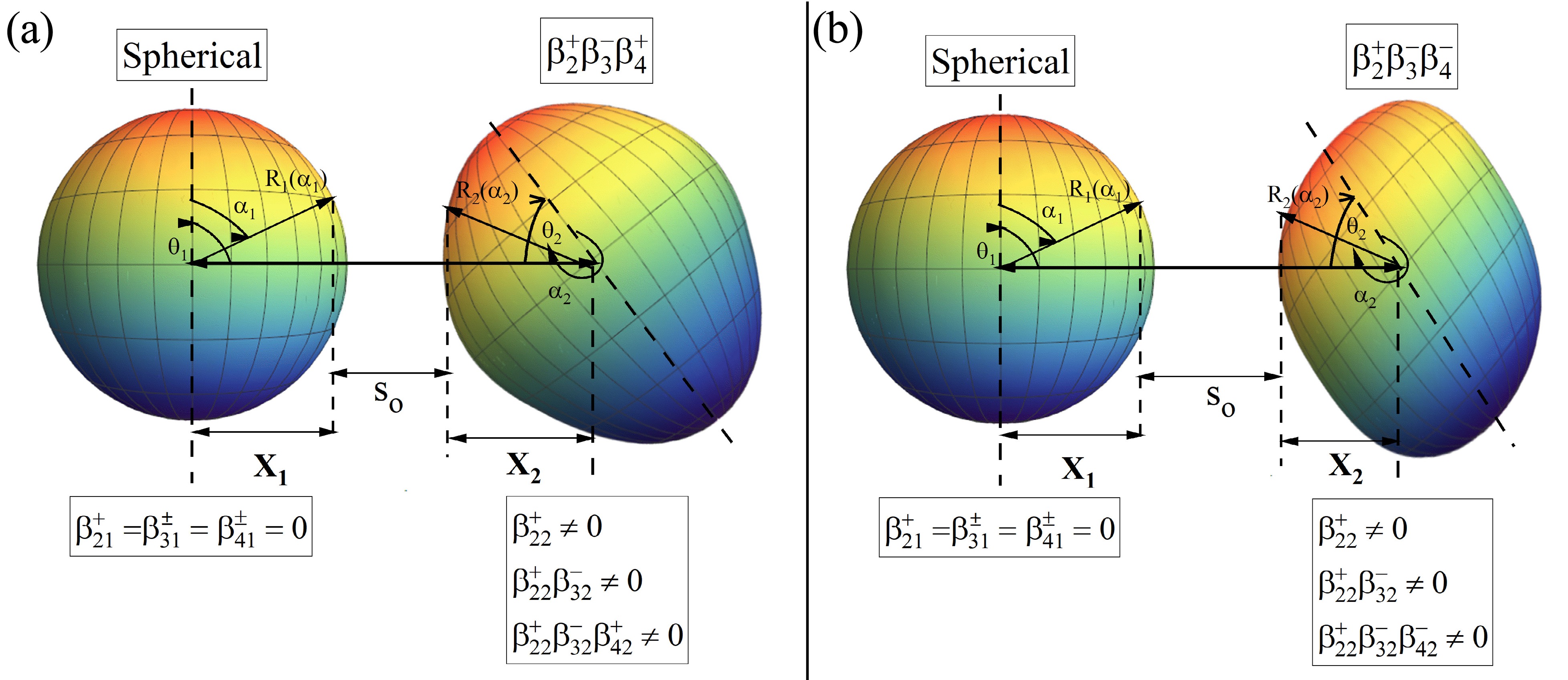

Figure 1.  (color online) Geometrical representation of (a) Spherical + $ \beta_2^+\beta_3^-\beta_4^+ $ and Spherical + $ \beta_2^+\beta_3^-\beta_4^- $ deformed nuclear partners colliding in a plane, with the minimum separation distance $ s_o $ between the two colliding surfaces facing each other is obtained using [45].

The present study aims to investigate the cumulative impact of the nuclear shape (due to higher-order deformations, upto $ \beta_4 $) on the dynamics of heavy-ion-induced fusion reactions. Additionally, we aim to scrutinize the effect of various signs of the considered deformations, namely ($ \beta_2^+\beta_3^+\beta_4^+ $, $ \beta_2^+\beta_3^+\beta_4^- $, $ \beta_2^+\beta_3^-\beta_4^+ $, $ \beta_2^+\beta_3^-\beta_4^- $, $ \beta_2^-\beta_3^+\beta_4^+ $, $ \beta_2^-\beta_3^+\beta_4^- $, $ \beta_2^-\beta_3^-\beta_4^+ $, $ \beta_2^-\beta_3^-\beta_4^- $), on the barrier characteristics. To conduct the analysis, we have considered the reactions with $ ^{148} {\rm{Nd}}$, $ ^{149} {\rm{Sm}}$, and $ ^{150} {\rm{Sm}}$ targets, which possess $ \beta_2 $, $ \beta_3 $, and $ \beta_4 $ deformations, with spherical beams of $ ^{16} {\rm{O}}$ and deformed beams of $ ^{32} {\rm{S}}$. The inclusion of higher order deformation provide better agreement with the available experimental data and helps to understand the collective influence of the shape of target nuclei on the reaction dynamics.

The present manuscript is organized as follows. In section.II, the formalism of the extended ℓ-summed Wong model and the contributing potentials used to pursue the present analysis are summarised. In section.III, the result and observations of the present analysis are discussed, followed by the summary of the manuscript in section. IV.

The shape of the deformed nuclear surface can be expressed through the radius vector $ R_i(\alpha_i) $, which involves the spherical harmonics $ Y_{\lambda}^{(0)}(\alpha_i) $ of higher-order, i.e., $ \lambda = 2,3,4 $ [57−60], as given below

here, i = 1, 2 correspond to projectile and target nuclei, respectively. $ R_{0i}( = 1.28A^{1/3}_i-0.76+0.8A^{-1/3}_i) $ in fm [61] represents the radius of the equivalent spherical nuclei. $ \beta_{\lambda i} $ is the static deformation parameter taken from the Data Table of M$ \ddot{o} $ller et al [60]. $ \lambda = 2,3,4 $ defines the quadrupole, octupole and hexadecapole deformed shapes, respectively. $ P_{\lambda}(\cos{\alpha_i}) $ is the Legendre polynomial. The detail of angles can be referred from [55]. The above radius term is input in the total interaction potential and its constituent terms, which are discussed below.

To study the heavy-ion induced reactions at the low-energy regime, the total interaction potential $ V_T(R) $ is considered as an important tool and defined as the combination of Coulomb potential $ V_C(R) $, centrifugal potential $ V_{\ell}(R) $ and nuclear potential $ V_N(R) $. The deformations (upto $ \beta_4 $) and relative orientation ($ \theta_i $) of deformed nuclei is incorporated in the above said contributing potentials. Thus, the total potential $ V_T(R,A_1,A_2,\beta_{\lambda{1}},\beta_{\lambda{2}},\theta_1,\theta_{2}) $ is defined as follows

where $ i = 1,2 $ represents the projectile and target nuclei respectively. The Coulomb potential $ V_C(R,Z_i,\beta_{\lambda i},\theta_i) $ for deformed-deformed pairs of colliding nuclei [62, 63] is defined as

It is important to note that for the spherical projectiles, the second term of above equation will have terms only for $ i = 2 $ i.e. deformed target, as $ \beta_{21} = 0.0 $ and $ \beta_{22}\neq0.0 $.

The centrifugal potential $ V_{\ell}(R,A_i,\beta_{\lambda i},\theta_i) $ in the form of rotational kinetic energy is given as

In Eq.(2), the nucleus-nucleus interaction potential $ V_N(R,A_i,\beta_{\lambda i},\theta_i) $ is defined on the basis of ‘Proximity Theorem’, given by Blocki et. al. [61] as the product of $ 4\pi\bar{R}\gamma b $, which is a function of the shape and geometry of the colliding nuclei, and $ \Phi(s_0) $, universal function depending on the shortest distance between the interacting nuclei [45, 61]. Thus, $ V_{N}(R,A_i,\beta_{\lambda i},\theta_i) $ is given as

here, $ s_0 $ is the minimum separation distance between the two facing surfaces of interacting nuclei. $ \bar{R} $ is the mean curvature radius expressed in terms of the radii of curvatures $ R_{i1} $ and $ R_{i2} $ for co-planar nuclei as [61]

The principal radii of curvature ($ R_{i1} $ and $ R_{i2} $) for spherical-deformed and deformed-deformed cases is given [64] as

Where $ R^{'}_i(\alpha_i) $ and $ R^{''}_i(\alpha_i) $ represent the first and second order derivatives, respectively, of radius vector $ R_i(\alpha_i) $ with respect to the angle $ \alpha_i $.

Important to note, for spherical projectiles, $ R_{11(\alpha_1)} = R_{12}(\alpha_1) = R_1(\alpha_1) $.

In Eq.(5) [61], γ is the surface energy constant and expressed for axially symmetric terms as,

‘b’ is the surface thickness having value 0.99 fm.

In Eq.(5), the universal function with single parameter $ s_0 $ is given as,

From Eqs. (2) - (9), defining the total interaction potential, one can get the detail of fusion barrier characteristics, i.e. barrier height $ V_B $, barrier position $ R_B $ and barrier curvature $ \hbar\omega_B $, which are influenced with the effect of deformation and orientation degrees of freedom. These terms are further utilized in the calculations of capture cross-sections.

The capture cross-section, in terms of angular momentum (ℓ) partial waves, for deformed and oriented nuclei, lying in the same planes and colliding with center of mass energy $ E_{c.m.} $, is defined using the extended ℓ-summed Wong formula of one-dimensional penetration model as

with $ k = \sqrt{\dfrac{2\mu E_{c.m.}}{\hbar^2}} $ and μ as the reduced mass. $ P_{\ell} $ is the transmission coefficient for each ℓ, which describes the penetration probability across the Coulomb barrier. Here, $ \ell_{max} $ is the maximum angular momentum calculated using the sharp cut-off approximation [65−68] for above barrier energies and extrapolated for the below barrier center of mass energies $ E_{c.m.} $ as given below.

In the present work, the penetration probability $ P_{\ell} $ has been obtained using the Hill-Wheeler [69] approximation, defined as follows,

respectively. The Hill-Wheeler approximation assumes a parabolic interaction barrier, resulting in the analytical expression for transmission that is commonly used in heavy ion fusion reactions, and thus, we have adopted it in our current study. In Eq.(12), $ V_{B}^{\ell} $, $ R_{B}^{\ell} $ and $ \hbar\omega_{B}^{\ell} $ represent the barrier height, barrier position and barrier curvature, respectively, which are extracted from the total interaction potential $ V_{T} $ [62]. Further, to observe the effect of deformations up to order of hexadecapole deformation over all the orientations, the fusion cross-sections are integrated over $ \theta_i $ with step of $ 10^o $ for spherical-deformed and deformed-deformed combination, as given below

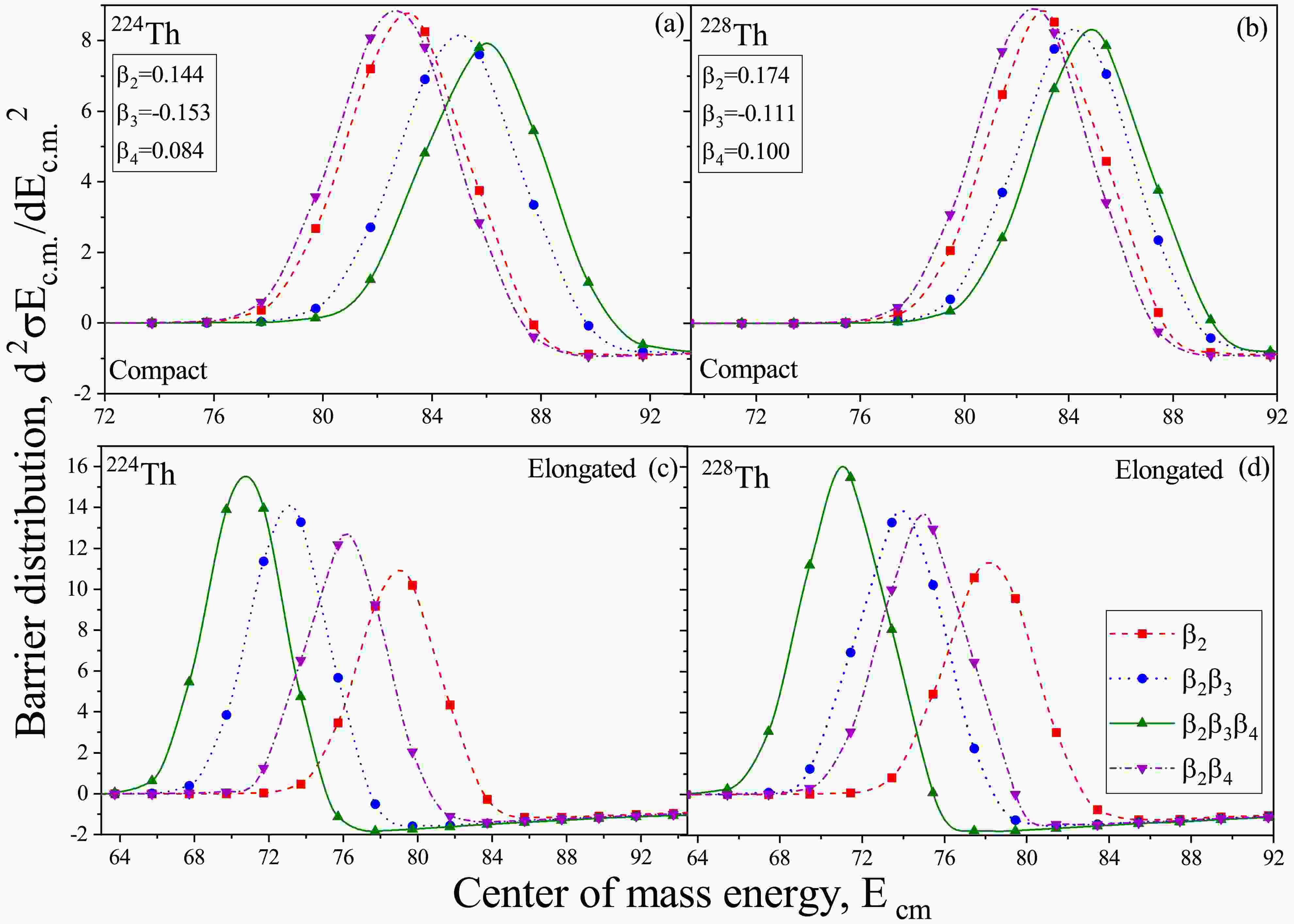
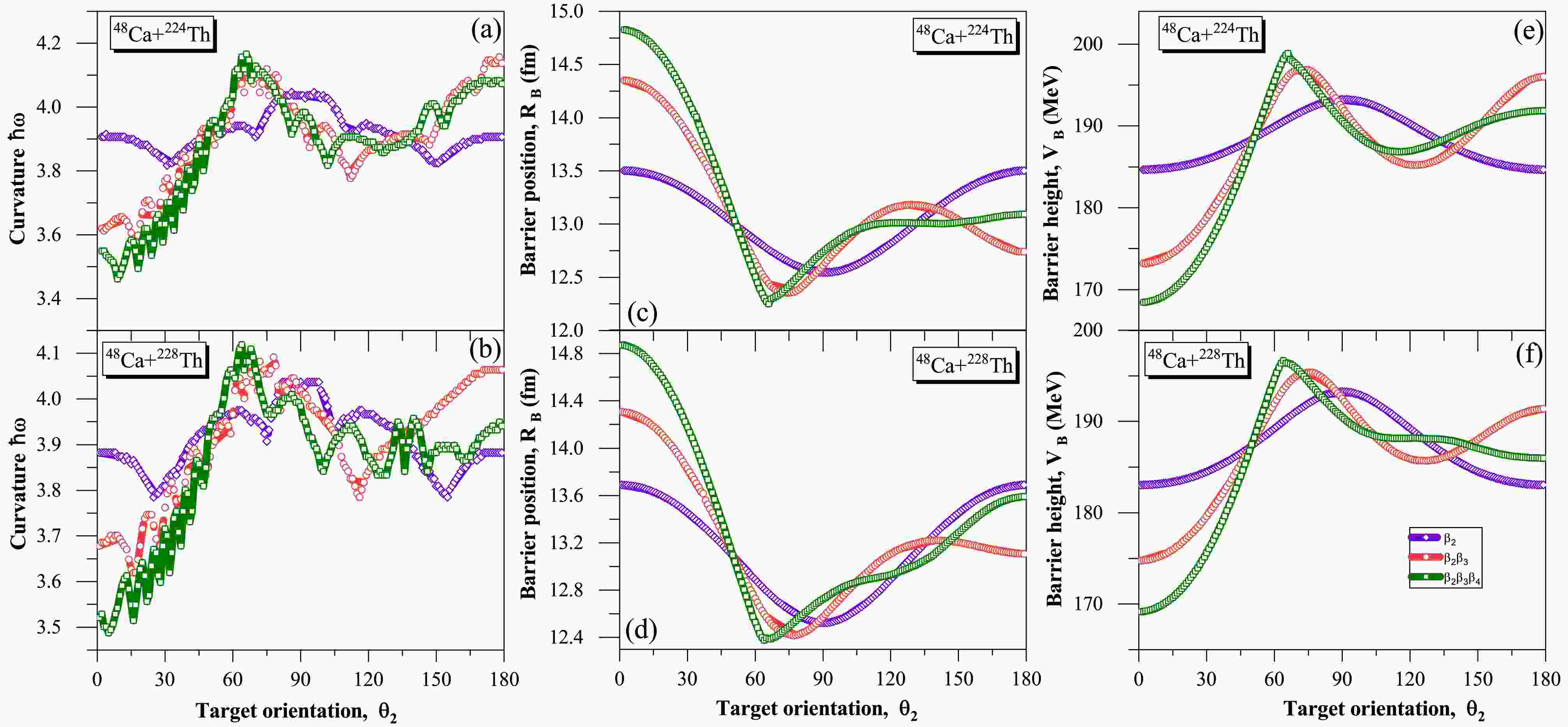
In the present study, we intend to analyze the collective influence of the sign and magnitude of higher order deformations on the fusion reaction dynamics by chronologically incorporating deformations up to $ \beta_4 $ (i.e. $ \beta_2 $, $ \beta_3 $, and $ \beta_4 $) of the target nuclei, with spherical as well as $ \beta_2 $ deformed projectiles. To perform an extensive analysis, we considered soft-deformed $ ^{228} {\rm{Th}}$ having the magnitude of octupole deformation lesser than the magnitude of quadrupole deformation (i.e. |$ \beta_3|<|\beta_2 $|) and the rigid deformed $ ^{224} {\rm{Th}}$ having the magnitude of octupole deformation higher than the magnitude of quadrupole deformation (i.e. $ \beta_3>\beta_2 $) of Th nuclei (Z = 90) having significant magnitudes of $ \beta_2 $, $ \beta_3 $ and $ \beta_4 $ deformations taken from the Data Table of M$ \ddot{o} $ller et al [60]. In order to examine the collective effect of these deformations, we performed calculations to observe the changes in curvature ($ \hbar\omega $), barrier position ($ R_B $), and barrier height ($ V_B $) with respect to the orientation of the target nuclei ($ \theta_2 $). This was achieved by sequentially incorporating the quadrupole $ \beta_2 $, octupole $ \beta_3 $, and hexadecapole $ \beta_4 $ deformations, as illustrated in Fig. 2. The figure clearly demonstrates distinct variations in the curvature $ \hbar\omega $, barrier position $ R_B $, and barrier height $ V_B $ as we incorporate deformations of increasing orders up to $ \beta_4 $. The figure not only portrays the significant modification in the barrier characteristics but also shows the variation in the orientation angle θ of compact and elongated configurations with inclusion of deformation of different orders.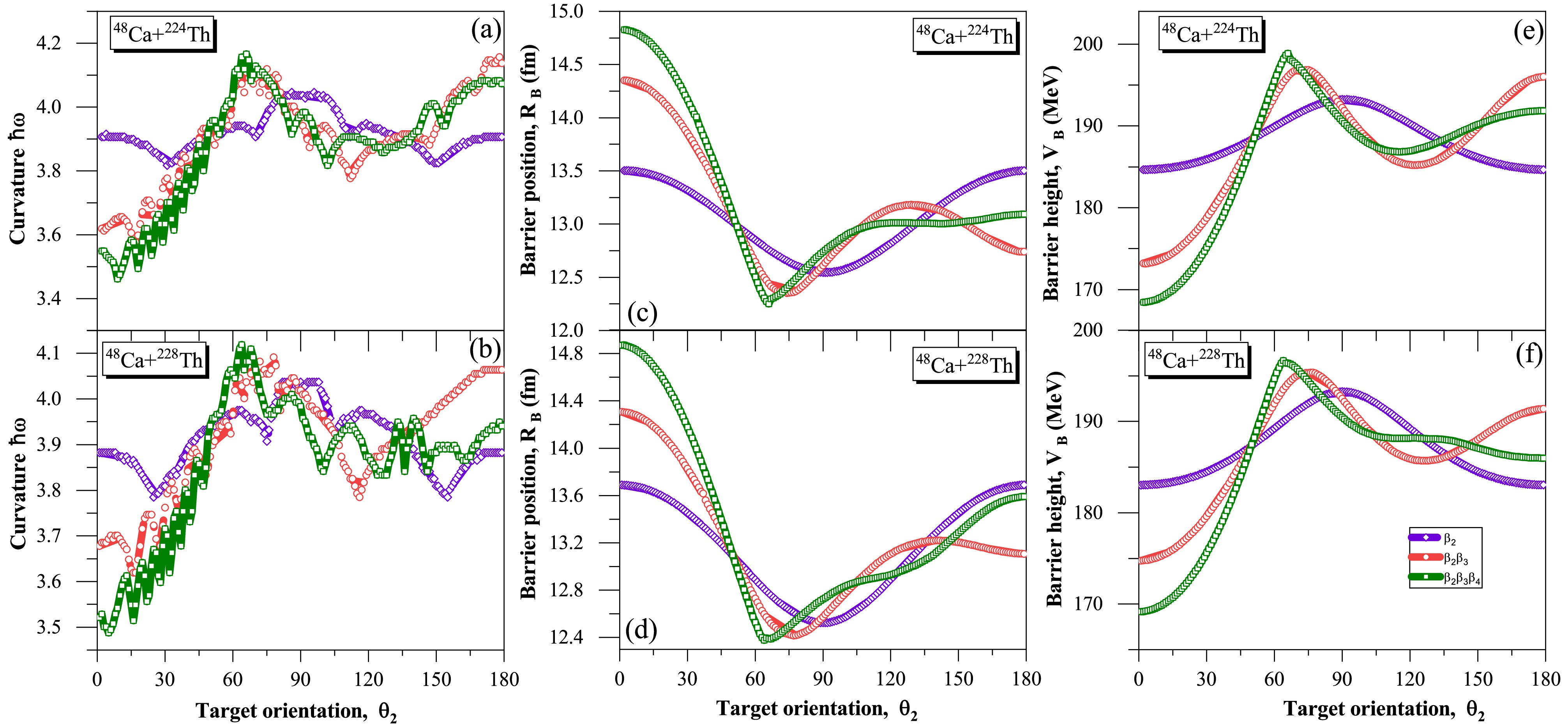

Figure 2.  (color online) The variation of the barrier height $ V_B $, with respect to the relative orientation $ \theta_2 $ of the soft ($ ^{228} {\rm{Th}}$) and rigid ($ ^{224} {\rm{Th}}$) $ \beta_2\beta_3\beta_4 $ deformed target nuclei, investigated for various combinations of $ \beta_2^{\pm},\beta_3^{\pm} $ and $ \beta_4^{\pm} $ deformations.

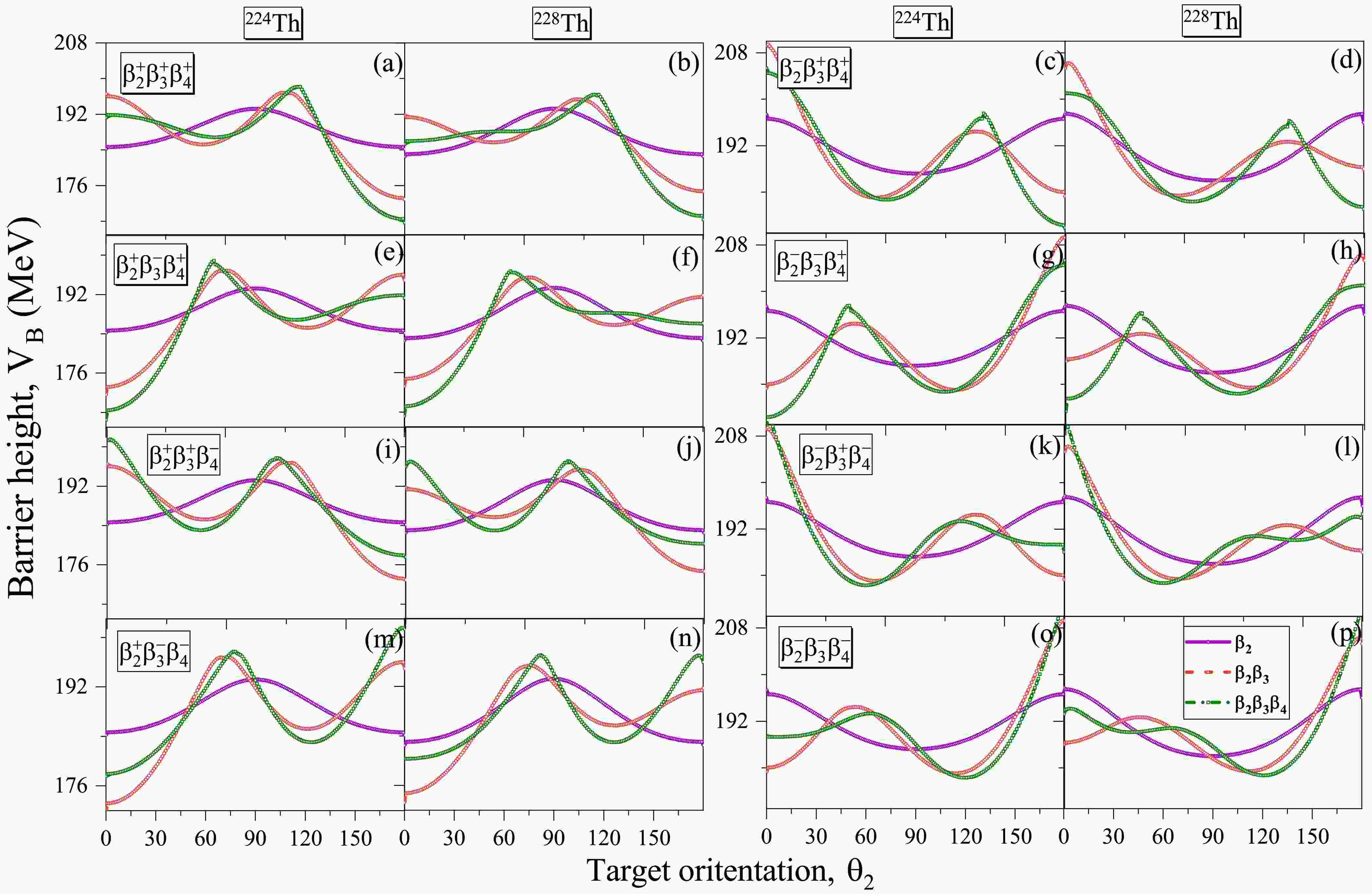
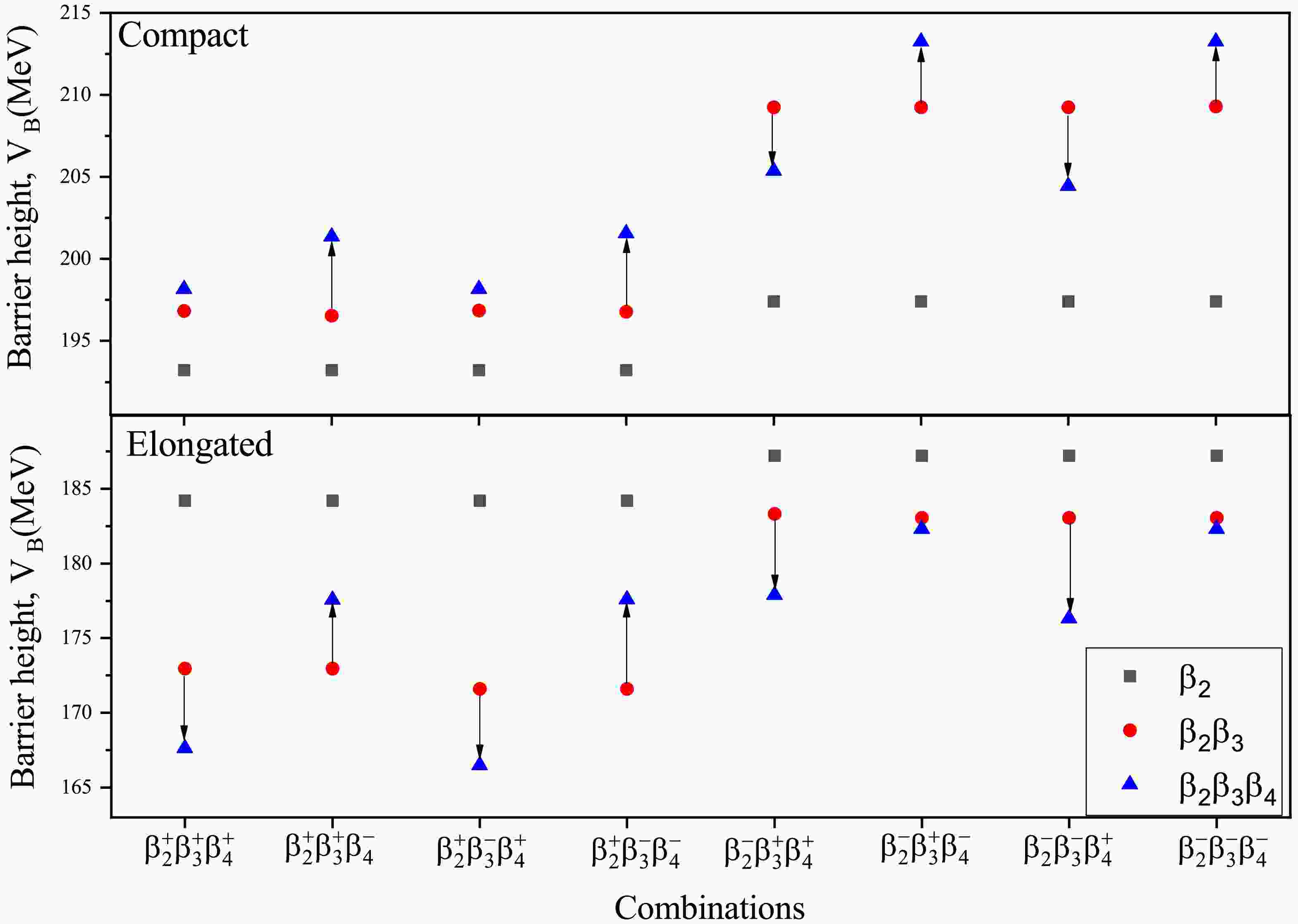
In order to explore the collective impact of higher order deformations in context of the signs of quadrupole ($ \beta_2 $), octupole ($ \beta_3 $), and hexadecapole ($ \beta_4 $) deformations, we have analysed the variation in the barrier height ($ V_B $) with respect to target orientation ($ \theta_2 $) for various configurations exhibiting unique sign combinations of these deformations. In particular, we examined the configurations $ \beta_2^+\beta_3^+\beta_4^+ $, $ \beta_2^+\beta_3^+\beta_4^- $, $ \beta_2^+\beta_3^-\beta_4^+ $, $ \beta_2^+\beta_3^-\beta_4^- $, $ \beta_2^-\beta_3^+\beta_4^+ $, $ \beta_2^-\beta_3^+\beta_4^- $, $ \beta_2^-\beta_3^-\beta_4^+ $, and $ \beta_2^-\beta_3^-\beta_4^- $, by changing the signs of deformations associated with $ ^{224} {\rm{Th}}$ and $ ^{228} {\rm{Th}}$ nuclei, taken from the Data Table of M$ \ddot{o} $ller et al [60] as illustrated in Fig. 3. The figure clearly demonstrates the significant variations in the barrier height $ V_B $ as the deformations are incorporated chronologically up to hexadecapole $ \beta_4 $ deformation. While experimental evidence supporting positive octupole deformation is not available, theoretical analysis based on theoretical values emphasizes that the maximum and minimum values of the barrier height $ V_B $ remain almost same despite alterations in the sign of the octupole deformation. Instead, there is a notable change in the orientation angle due to inversion of symmetry corresponding to maximum and minimal barrier height $ V_B $. To investigate these variations and to comprehend the collective behavior, we have analyzed the alterations in the barrier height $ V_B $ for the considered combinations of deformations with different signs and orders as depicted in Fig. 4. In this figure, the variation in the barrier height $ V_B $ is depicted based on different combinations of deformations. From the figure one can observe that there is a significant decrease in the barrier height $ V_B $ when positive hexadecapole deformation $ \beta_4^+ $ is involved, while a notable increase is observed with negative hexadecapole deformation $ \beta_4^- $. Interesting to note that all the configurations are following the said trend, with the exception of the configurations involving $ \beta_2 $ and $ \beta_4 $ deformation of the same sign. For instance $ \beta_2^+\beta_3^{\pm}\beta_4^+ $ and $ \beta_2^-\beta_3^{\pm}\beta_4^- $ combinations show the same trend but only at one of the compact or elongated configuration and opposite or almost no change is observed for the other configuration. For example, in combination $ \beta_2^+\beta_3^{\pm}\beta_4^+ $ the lowering of barrier height $ V_B $ can be observed only at elongated configuration as the expansion in the nuclear shape due to addition of $ \beta_4^+ $ is significant along the major axis while small expansion is observed along the minor axis for this shape, and vise versa for the $ \beta_2^-\beta_3^{\pm}\beta_4^- $ combination. Similar pattern is observed for the $ ^{228} {\rm{Th}}$ isotope. The analysis extends to the barrier position $ R_B $, where combinations with positive hexadecapole deformation $ \beta_4^+ $ show an increment in $ R_B $, while those with negative hexadecapole deformation experience a decrement in $ R_B $ when combined with $ \beta_2^{\pm}\beta_3^{\pm} $. These changes in $ V_B $ and $ R_B $ impart corresponding impact on orientation angle of elongated and compact configurations (based on the sign of the quadrupole deformation $ \beta_2 $). Such enhancement/decrement in the barrier characteristics due to the considered combinations gives rise to new compact and elongated configurations.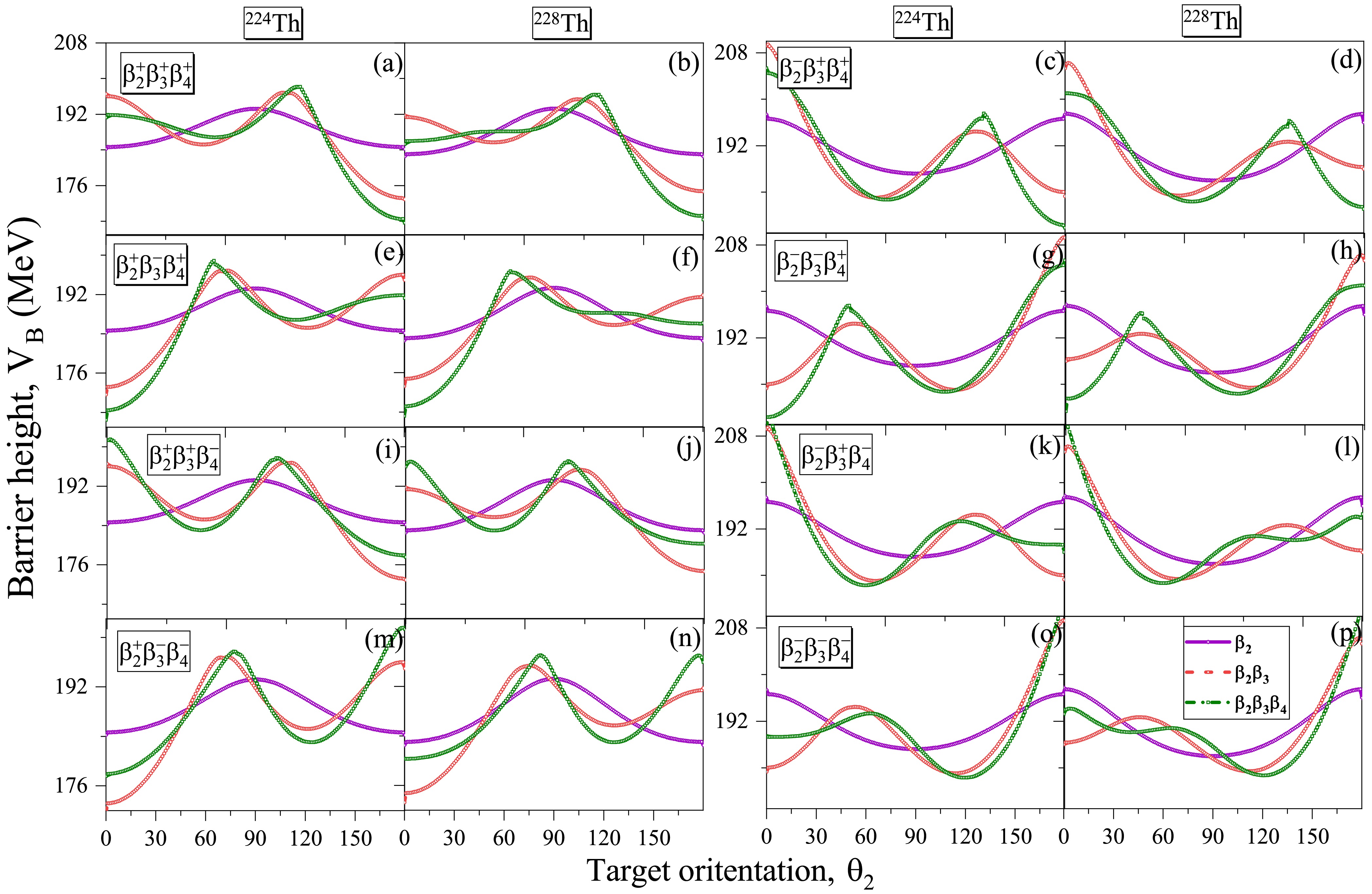

Figure 3.  (color online) The variation of the barrier height $ V_B $, with respect to the relative orientation $ \theta_2 $ of the soft ($ ^{228} {\rm{Th}}$) and rigid ($ ^{224} {\rm{Th}}$) $ \beta_2\beta_3\beta_4 $ deformed target nuclei, investigated for various combinations of $ \beta_2^{\pm},\beta_3^{\pm} $ and $ \beta_4^{\pm} $ deformations.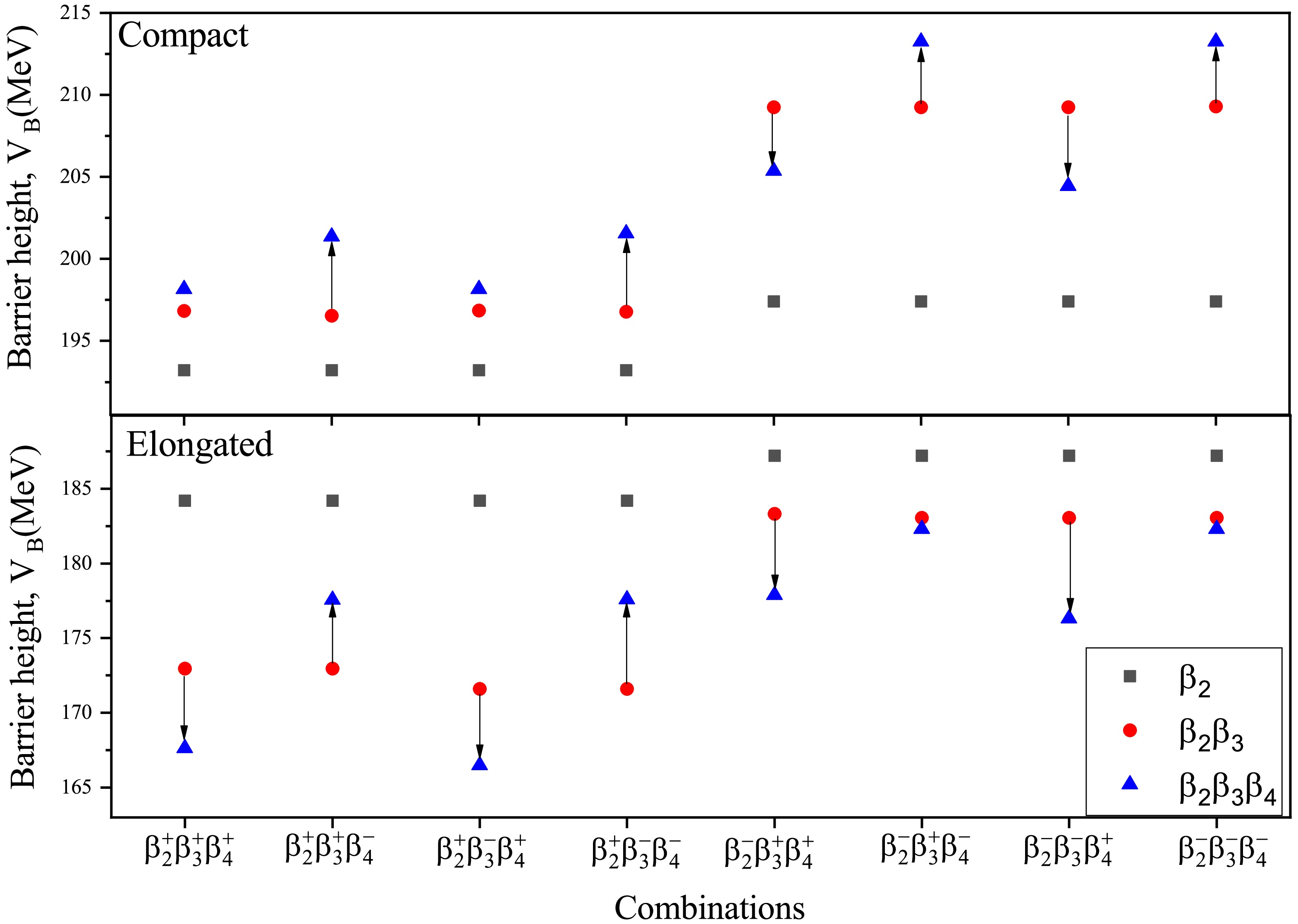

Figure 4.  (color online) The variation of the barrier height $ V_B $ investigated for various combinations of $ \beta_2^{\pm},\beta_3^{\pm} $ and $ \beta_4^{\pm} $ deformations of $ \beta_2\beta_3\beta_4 $ deformed target nuclei $ ^{224} {\rm{Th}}$ at their respective compact and elongated configurations.

Based on the above results, the variations in $ V_B $ and $ R_B $ due to the collective incorporation of deformations of different order and signs mainly $ \beta_3 $ and $ \beta_4 $, in conjunction with the quadrupole deformation $ \beta_2 $ led us to analyze the collective and specific effects of higher-order deformations on the overall nuclear reaction dynamics. To perform this analysis extensively, we have selected the reactions involving the $ \beta_2\beta_3\beta_4 $ deformed nuclei ($ ^{148} {\rm{Nd}}$, $ ^{149,150} {\rm{Sm}}$) as target nuclei, with spherical ($ ^{16} {\rm{O}}$) and $ \beta_2 $ deformed ($ ^{32} {\rm{S}}$) projectile beams. To generalize our results, we have investigated the variation in the barrier characteristics, namely $ V_B $, $ R_B $, and $ \hbar\omega $, corresponding to the target orientation $ \theta_2 $, for the chronological incorporation of quadrupole ($ \beta_2 $), octupole ($ \beta_2\beta_3 $), and hexadecapole ($ \beta_2\beta_3\beta_4 $) deformations, as depicted in Fig. 5 for the considered reactions. The figure illustrates similar changes in the curvature ($ \hbar\omega $), barrier position ($ R_B $), and barrier height ($ V_B $) for the considered reactions, represented by Fig. 5(a-d), Fig. 5(e-h), and Fig. 5(i-l), respectively as observed in Fig. 2. That is, for the elongated configuration (at $ \theta_2 = 0^o $), the incorporation of $ \beta_4^+ $ along with $ \beta_2^{\pm}\beta_3^{\pm} $ leads to elongation of nuclear shape which results in the lowering of barrier height $ V_B $ and an increase in the barrier position $ R_B $ consistently. In addition to the magnitude of these parameters, we also observed a significant shift in the orientation angle of the compact and elongated configurations as we progressed toward higher-order deformations as predicted in [56].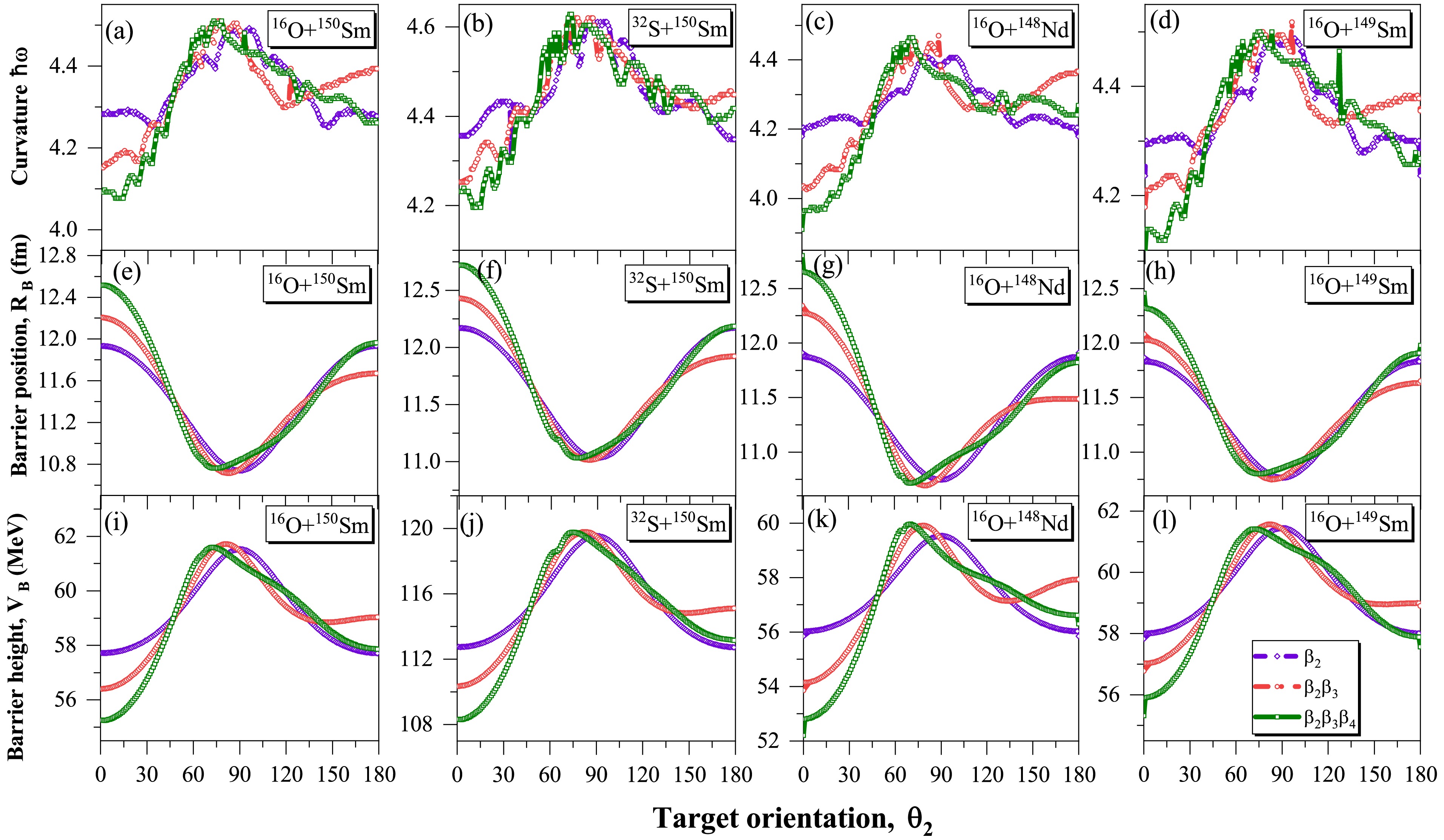

Figure 5.  (color online) The variation of the barrier curvature $ \hbar\omega $ (a-d), barrier position $ R_B $ (e-h) and barrier height $ V_B $ (i-l), with respect to the relative orientation $ \theta_2 $ of the $ \beta_2^+\beta_3^-\beta_4^- $ deformed target nuclei for the P-T combinations $ ^{16} {\rm{O}}$+$ ^{150} {\rm{Sm}}$, $ ^{32} {\rm{O}}$+$ ^{150} {\rm{Sm}}$, $ ^{16} {\rm{O}}$+$ ^{148} {\rm{Nd}}$ and $ ^{16} {\rm{O}}$+$ ^{149} {\rm{Sm}}$, respectively.

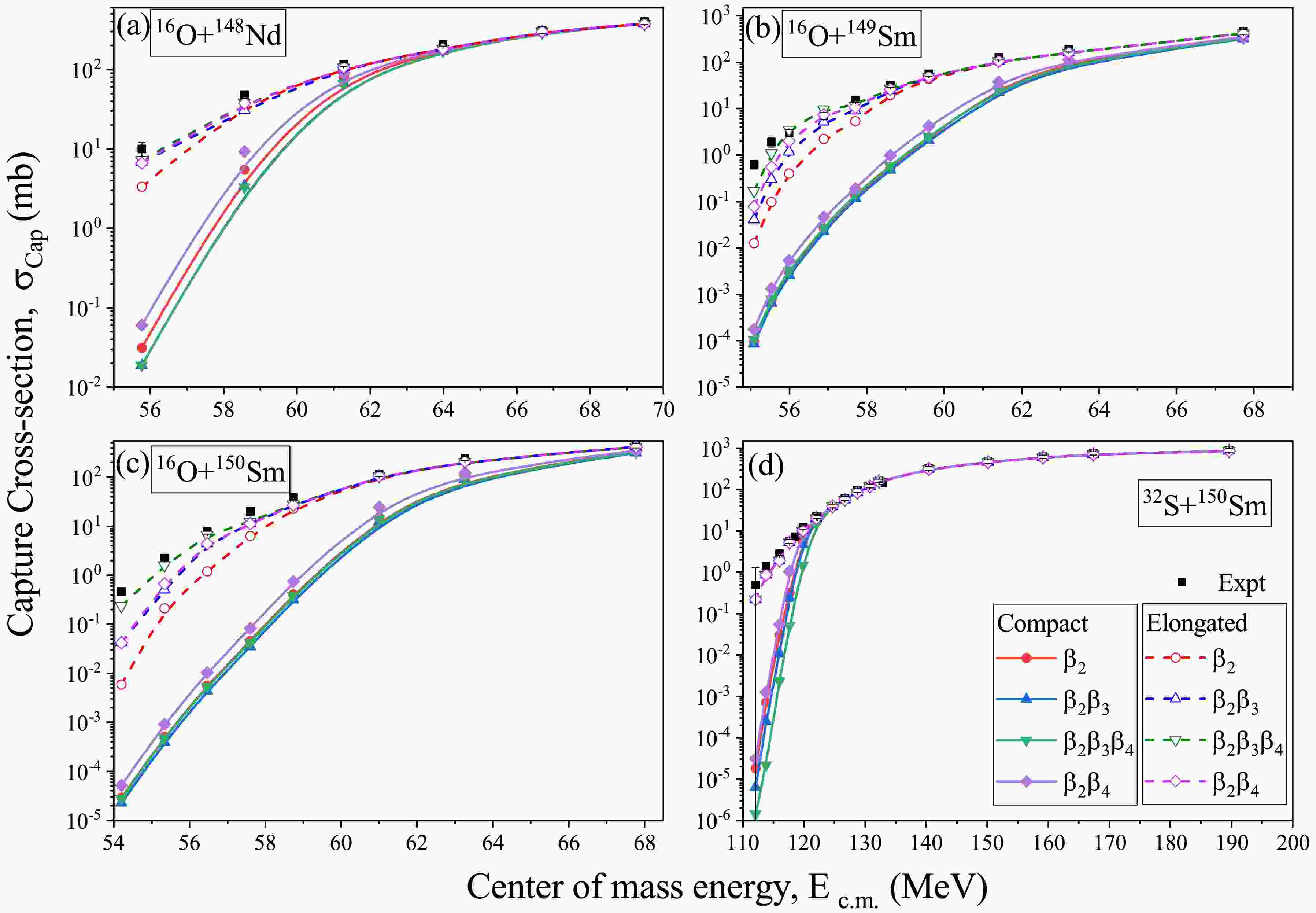
In continuation of the above findings, we analyzed the corresponding effects of these variations in the barrier height $ V_B $, barrier position $ R_B $, and barrier curvature $ \hbar\omega $ on the capture cross-section $ \sigma_{cap}(E_{c.m.}) $ of the considered P-T combinations obtained by the extended ℓ-summed model. In Fig. 6, the change in the capture cross-section $ \sigma_{cap}(E_{c.m.}) $ for different combinations of quadrupole $ \beta_2 $, octupole $ \beta_3 $, and hexadecapole $ \beta_4 $ deformations at their respective compact and elongated configurations is shown. From this figure, one can see the variation in the capture cross-section as we consider and incorporate different combinations of deformations up to $ \beta_4 $, i.e., $ \beta_2, \beta_2\beta_3, \beta_2\beta_3\beta_4 $ and $ \beta_2\beta_4 $ for compact and elongated configuration for across the barrier center of mass energies $ E_{c.m.} $. The calculated $ \sigma_{cap}(E_{c.m.}) $ for all the considered cases are compared with the available experimental data [71−73]. Though the experimental data includes all orientation, With this comparison, we have analyzed that the improvement in the cross-sections as one moves from compact configuration to spherical to elongated configuration of $ \beta_2\beta_3\beta_4 $ deformation, especially at the below and near barrier energies. However, there is still some hindrance observed in $ \sigma_{cap}(\beta_2\beta_3\beta_4) $(Elong.) from $ \sigma_{cap}^{Expt} $ for some cases, mainly at the sub-barrier region which can be further explored by including some other degree of freedom like non-axial or non-coplanar symmetries. Note that, to observe the average effect of orientation degree of freedom and not constrained to the specified compact or elongated configurations, the integrated cross-sections' over all mutual orientations of the deformed nuclei are calculated and shown in Fig. 7. The experimental data include all orientations, however, the comparison between the calculated cross sections for compact and elongated configurations and the experimental data is being conducted to demonstrate and understand the consistency of the results for a particular orientation of the target nuclei corresponding to the highest and lowest barrier height $ V_B $. In relation to the experimental aspect, we have additionally calculated the cross-sections integrated across all orientations to strengthen our findings in Fig. 7. The integrated crosssections in Fig. 7 are plotted for different combinations of deformations up to $ \beta_4 $, i.e., $ \beta_2, \beta_2\beta_3, \beta_2\beta_3\beta_4 $ and $ \beta_2\beta_4 $. One can see that the integrated cross-sections also confirm minor enhancement in the cross-sections after the incorporation of deformations up to $ \beta_4 $. It is also to be noted that the target nuclei considered in the present work exhibit positive hexadecapole deformation $ \beta_4^+ $ only. Consequently, the inclusion of deformations up to $ \beta_4 $ reduce the potential barrier, thereby enhancing the capture cross sections $ \sigma_{cap} $. Conversely, if the considered target nuclei had negative hexadecapole deformation $ \beta_4^- $, the inclusion of deformations up to $ \beta_4 $ would have resulted in an increased potential barrier, ultimately hindering the capture cross sections.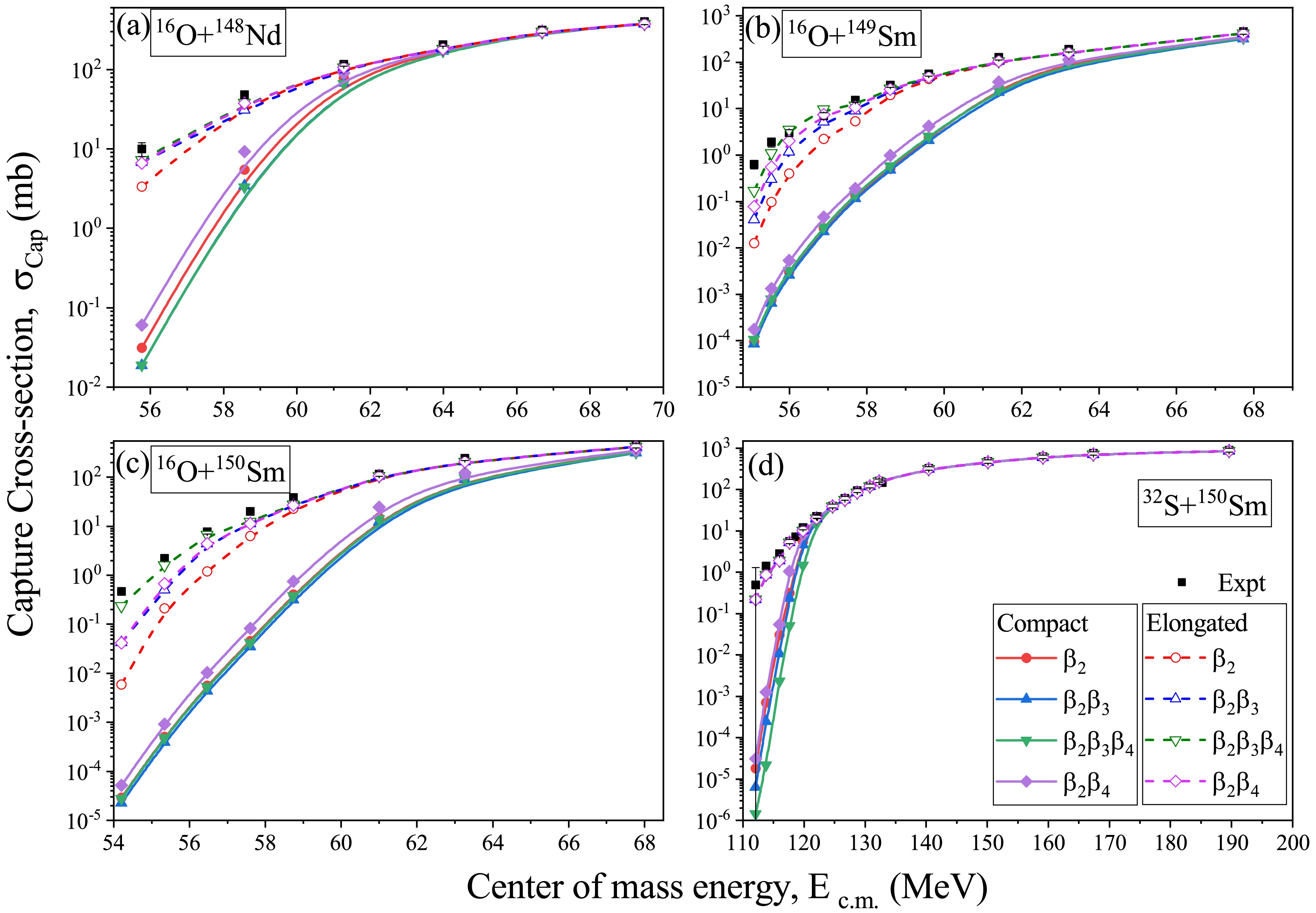

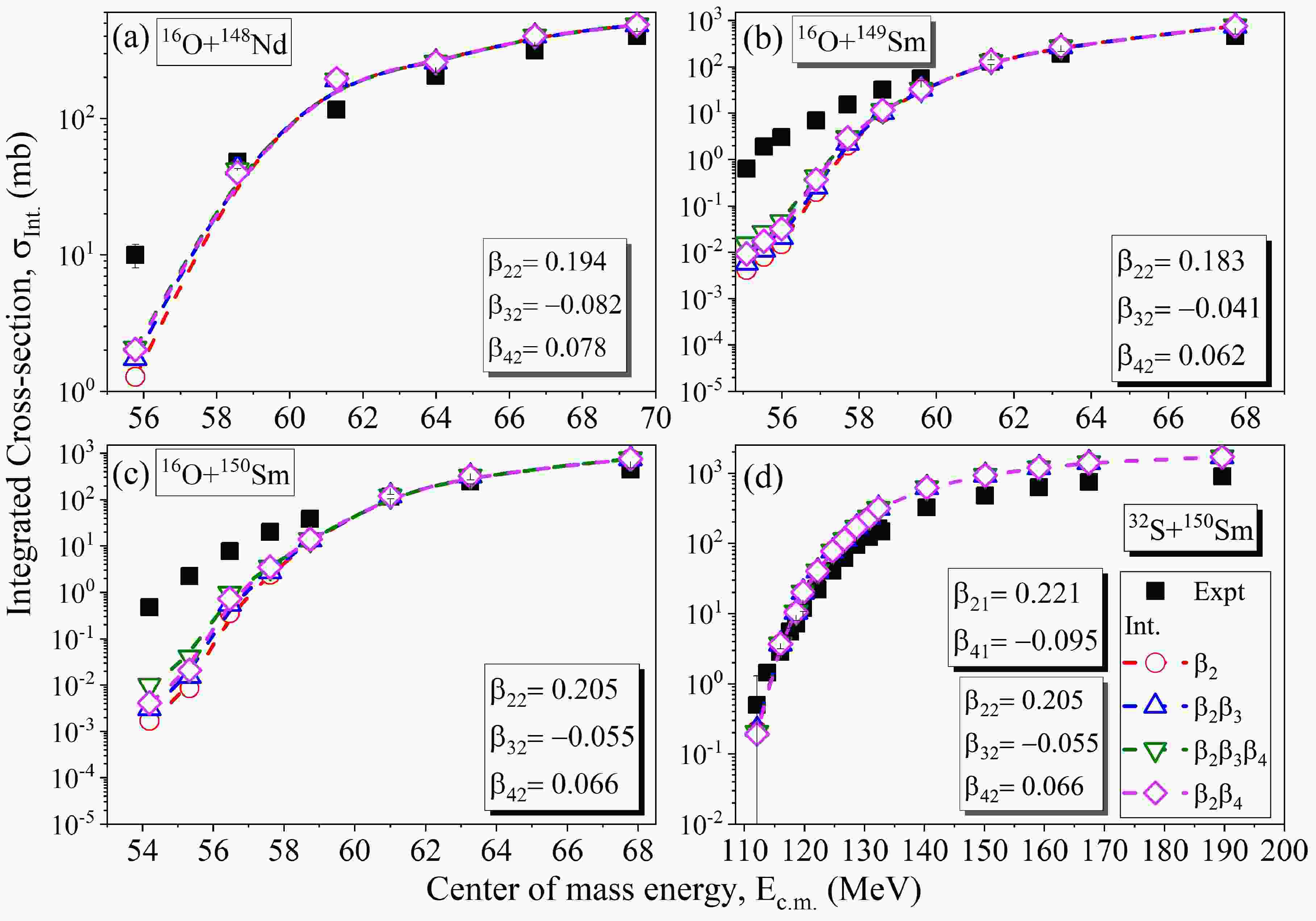
Figure 6.  (color online) The capture cross-sections ($ \sigma_{cap} $) calculated using extended ℓ-summed Wong model [70] for the P-T combinations (a) $ ^{16} {\rm{O}}$+$ ^{148} {\rm{Nd}}$, (b) $ ^{16} {\rm{O}}$+$ ^{149} {\rm{Sm}}$, (c) $ ^{16} {\rm{O}}$+$ ^{150} {\rm{Sm}}$ and (d) $ ^{32} {\rm{S}}$+$ ^{150} {\rm{Sm}}$ respectively, as a function of $ E_{c.m.} $. The calculated $ \sigma_{cap} $ for considered choices of projectile-target combinations is compared with the available experimental data for incident energies lying across the Coulomb barrier.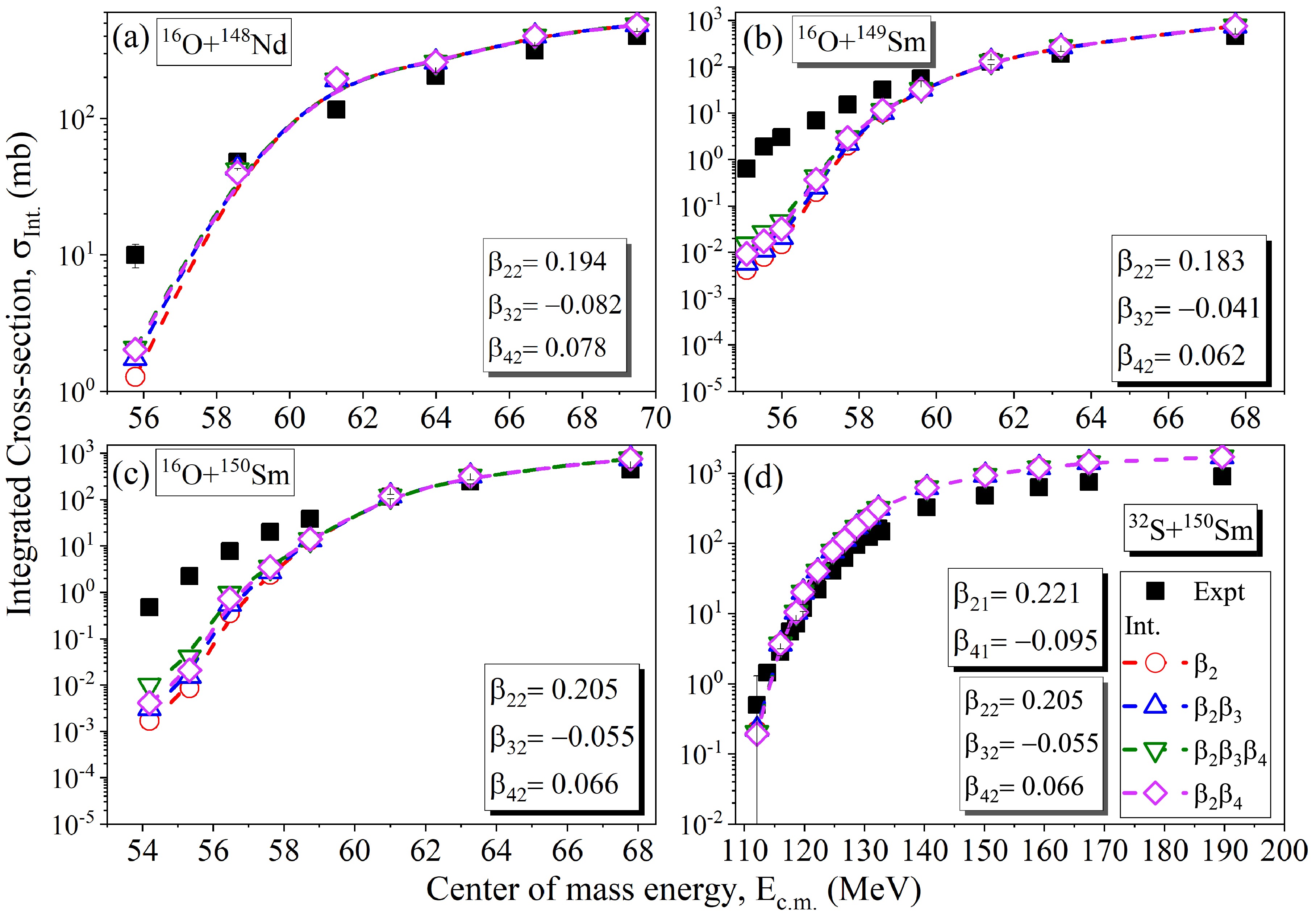

Figure 7.  (color online) The capture cross-sections integrated over possible orientations ($ \sigma_{Int} $) calculated using extended ℓ-summed Wong model [70] for the P-T combinations (a) $ ^{16} {\rm{O}}$+$ ^{148} {\rm{Nd}}$, (b) $ ^{16} {\rm{O}}$+$ ^{149} {\rm{Sm}}$, (c) $ ^{16} {\rm{O}}$+$ ^{150} {\rm{Sm}}$ and (d) $ ^{32} {\rm{S}}$+$ ^{150} {\rm{Sm}}$ respectively, as a function of $ E_{c.m.} $. The calculated $ \sigma_{Int} $ for considered choices of projectile-target combinations is compared with the available experimental data for incident energies lying across the Coulomb barrier.

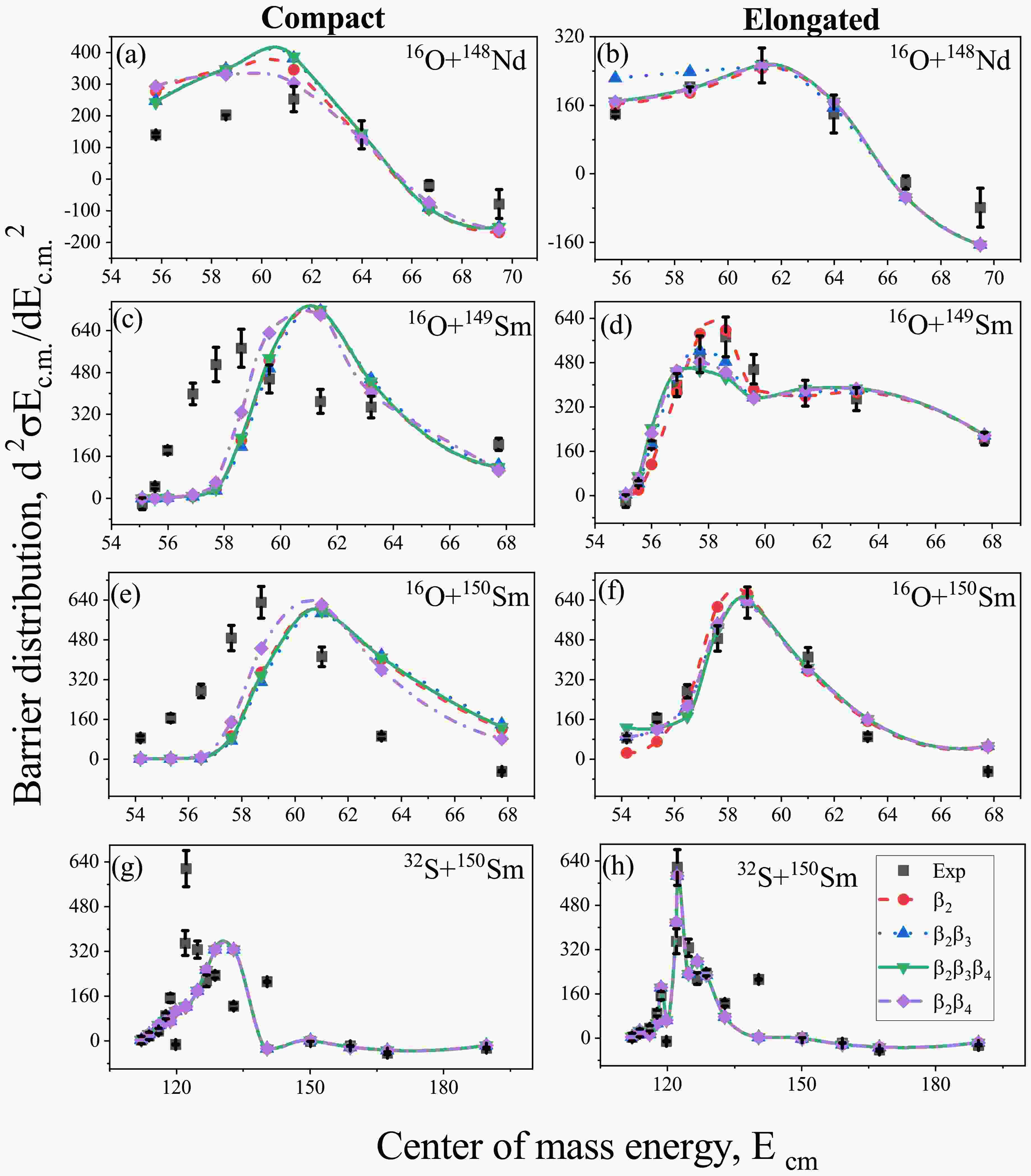
In order to gain insight into the dynamics of the reaction, we performed an analysis of the barrier distributions $ d^2{\sigma}E_{c.m.}/{dE_{c.m.}}^2 $ for various combinations of deformations of different orders, with respect to the center of mass energy $ E_{c.m.} $. The obtained results were then compared with the experimental barrier distributions for both the compact and elongated configurations, as depicted in Fig. 8. In this figure the barrier distribution of chronological incorporation of deformation up to $ \beta_4 $ is shown for both the compact and elongated configurations. It is worth noting that the $ \beta_3 $ and $ \beta_4 $ deformations for the considered reactions have lower magnitude than the $ \beta_2 $ deformation. Thus, the impact of higher-order deformations on the barrier distribution is not observable. But on examination of the figure, we see a trend of the distribution with the peaks analogous to the associated deformations of the P-T deformations. It also becomes evident that the results obtained for the elongated configurations align more closely with the experimental distributions than the compact configurations. Consequently, the cross-sections derived from the elongated configurations offer more compelling evidence when compared to the experimental data. Strengthening the fact that the incorporation of all the deformation up to $ \beta_4 $ provides a better insight in the dynamics of the reaction dynamics.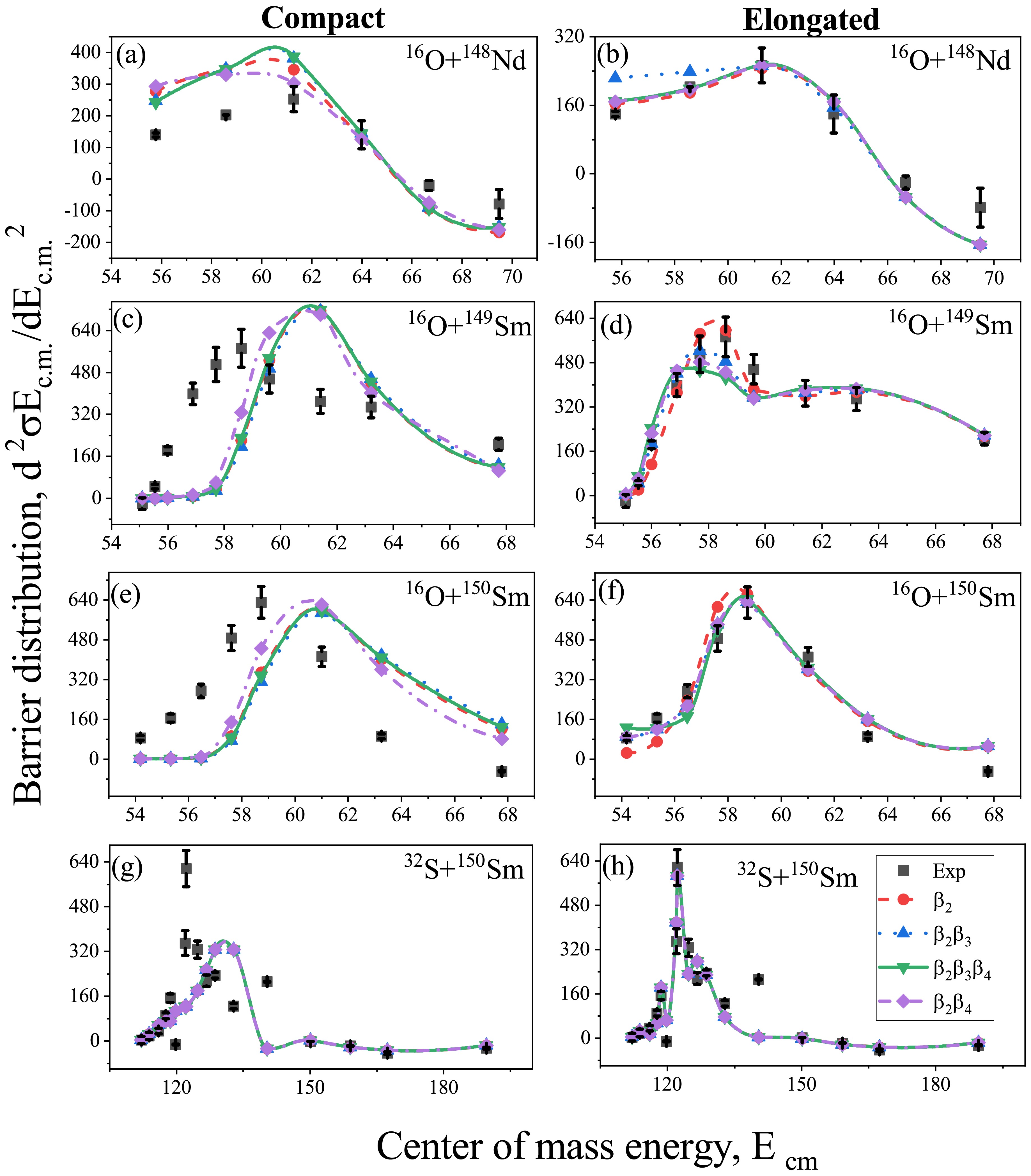

Figure 8.  (color online) Barrier distribution of different combinations of deformations for the P-T combinations (a) $ ^{16} {\rm{O}}$+$ ^{148} {\rm{Nd}}$, (b) $ ^{16} {\rm{O}}$+$ ^{149} {\rm{Sm}}$, (c) $ ^{16} {\rm{O}}$+$ ^{150} {\rm{Sm}}$ and (d) $ ^{32} {\rm{S}}$+$ ^{150} {\rm{Sm}}$ respectively, as a function of center of mass energy $ E_{c.m.} $. The calculated $ d^2{\sigma}E_{c.m.}/{dE_{c.m.}}^2 $ for considered choices of projectile-target combinations is compared with the available experimental data [71−73] for incident energies lying across the Coulomb barrier.

Now to examine the impact of these higher-order deformations on the distribution of barriers, we performed calculations on the barrier distributions for the soft and rigid deformed Th isotopes. These calculations are based on the capture cross-sections obtained at various center of mass energies across the barrier, considering both the Compact and elongated configurations. The results are presented in Fig 9(a-b) and Fig 9(c-d) respectively. By analyzing this figure, one can observe the differences in the distribution as we progressively incorporated the higher order deformations $ \beta_3 $ and $ \beta_4 $. Notably, there is a noticeable deviation in the position of the peak and a variation in the height of the peak, including all the deformations up to $ \beta_4 $. This figure provides insights into the shifting of the barrier distribution curves with the inclusion of higher-order deformations. Specifically, the shift in the peak position of the barrier distribution for both the compact and elongated configurations indicates a change in the barrier height and the corresponding barrier energy as we incorporate the higher order deformations in addition to $ \beta_2 $. The peaks shift towards higher energies for the compact configurations as the higher-order deformations are included. Conversely, for the elongated configurations, the peaks shift towards lower energies with the inclusion of higher-order deformations reflecting the change in the barrier characteristics after the incorporation of higher-order deformations. Additionally, the inclusion of these higher-order deformations leads to a significant change in the peak height, thereby increasing the feasibility of the reaction.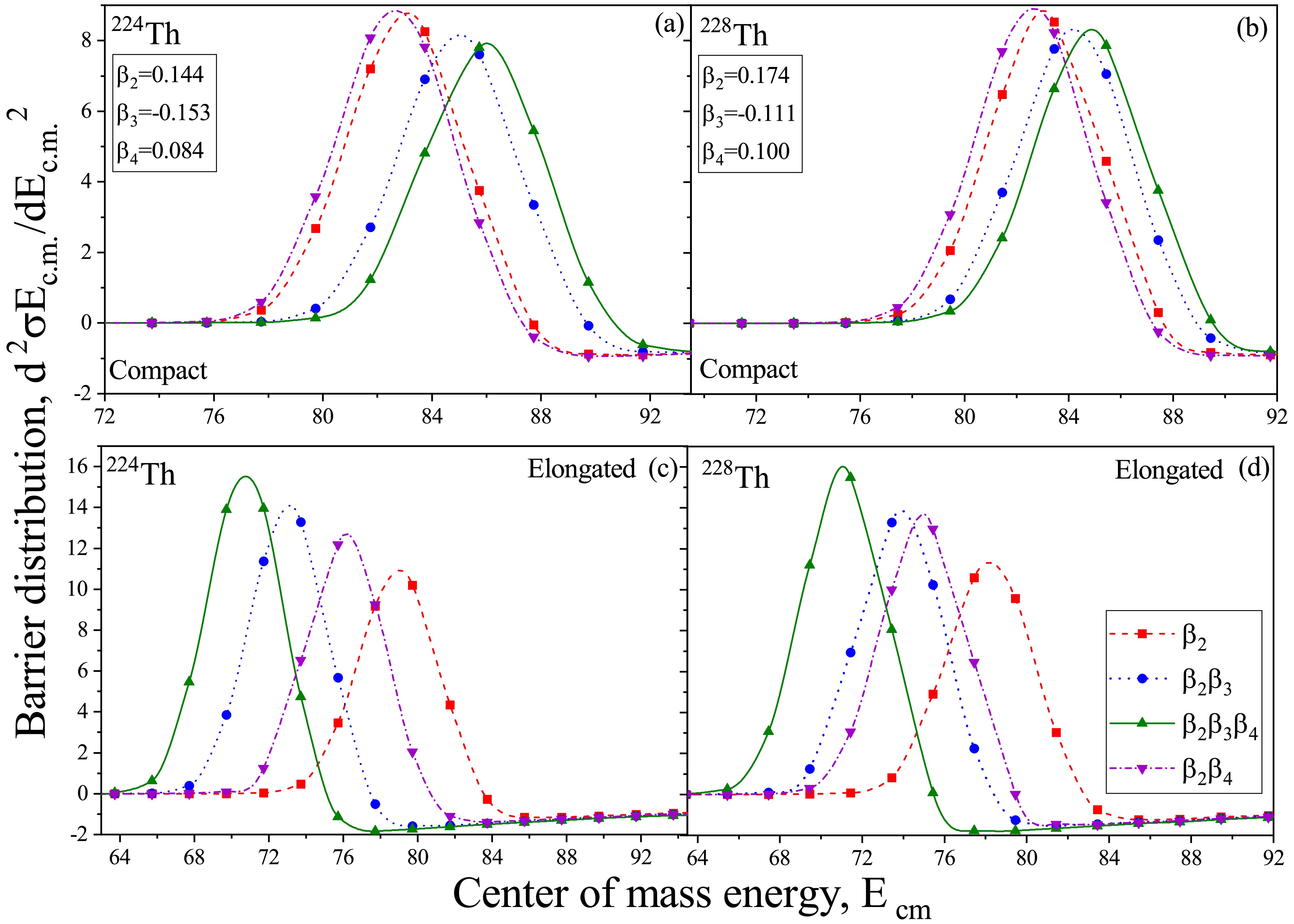

Figure 9.  (color online) The barrier distribution i.e.$ d^2{\sigma}E_{c.m.}/{dE_{c.m.}}^2 $ of different combinations of deformations for $ ^{224} {\rm{Th}}$ and $ ^{228} {\rm{Th}}$ i.e. $ \beta_2 $, $ \beta_2\beta_3 $, $ \beta_2\beta_3\beta_4 $ and $ \beta_2\beta_4 $ at their (a-b) compact and (c-d)elongated configuration respectively, as a function of the center of mass energy $ E_{c.m.} $ lying across the Coulomb barrier.

In essence, deformations upto order of $ \beta_4 $ collectively influences the barrier characteristics and cross-sections. Neglecting any order of deformation can lead to significant deviations in the outcomes. Therefore proper inclusion of higher order deformations is desirable for better understanding of the nuclear dynamics.

In the present study, an analysis was performed to examine the collective relevance of higher-order deformations, specifically up to hexadecapole $ \beta_4 $ deformation. This analysis utilized $ \beta_2\beta_3\beta_4 $ deformed targets and investigated their impact on the fusion barrier characteristics and fusion cross sections. The calculations are performed at $ \theta_{opt} $ for both "elongated" and "compact" configurations of the interacting deformed nuclei, to address the reaction dynamics across the Coulomb barrier.

It is observed that nuclei possessing all three deformations, namely $ \beta_2 $, $ \beta_3 $, and $ \beta_4 $ (such as $ ^{148} {\rm{Nd}}$, $ ^{149,150} {\rm{Sm}}$), provide a precise insight of fusion barrier characteristics and reaction dynamics when the deformations up to hexadecapole $ \beta_4 $ are incorporated.

Furthermore, a comparison was made between the theoretically calculated capture cross-sections ($ \sigma_{cap} $) and the available experimental data for reactions involving $ \beta_2\beta_3\beta_4 $ deformed target nuclei. It was discovered that the calculated $ \sigma_{cap} $ using the extended ℓ-summed Wong model improved significantly when all deformations up to $ \beta_4 $ were incorporated, along with the corresponding elongated optimum orientations across the Coulomb barrier. Along with the cross-sections, the barrier distribution curves also provide a good agreement with the experimental results after incorporating deformations of all orders up to $ \beta_4 $ at the elongated configurations.

In conclusion, the comprehensive examination of deformations up to $ \beta_2\beta_3\beta_4 $ yields a more comprehensive understanding of the fusion barrier characteristics and reaction dynamics compared to the $ \beta_2 $ and $ \beta_2\beta_3 $ scenarios. The aforementioned analysis has confirmed that the inclusion of $ \beta_4^+ $ deformation in $ \beta_2^{\pm}\beta_3^{\pm} $ enhances the reaction cross sections, while the incorporation of $ \beta_4^- $ deformation in $ \beta_2^{\pm}\beta_3^{\pm} $ hinders the reaction cross sections. This study addresses inquiries about the collective impact of deformations up to $ \beta_4 $ on the reaction dynamics. Present study also raises question regarding the need of additional degree of freedom like the non-axial or non-coplanar degree of freedom in both the entrance and exit channels of nuclear interactions. Therefore it will be of interest to incorporate the non-coplanar interactions in our next problem. Such theoretical analysis will contribute to a more comprehensive understanding of the structural properties, stability, and dynamics of nuclear interactions involving higher-order deformed nuclei.

The research projects of the Science and Engineering Research Board (SERB), File Nos. CRG/2021/001229 and CRG/2021 /001144, are gratefully acknowledged.