Triply charmed baryons mass decomposition from lattice QCD

Since the discovery of the $ J/\psi $ meson in 1974 [1, 2], charm physics has garnered significant attention, leading to the identification of numerous charmed hadrons. Recently, the Large Hadron Collider (LHC) has made notable advancements in the study of charmed baryons, including the spectroscopy of excited hadrons such as $ \Lambda_{c}^{+} $ [3], $ \Omega_{c}(X) $ [4], and $ \Xi_{c}(X) $ [5]. Notably, the doubly charmed baryon $ \Xi_{cc}^{++} $ was established by LHCb in 2017 [6] and has since been confirmed by subsequent studies [7, 8], following the initial identification of the charmed baryon $ \Lambda_{c} $ by Mark-II in 1979 [9]. However, the triply charmed baryon has yet to be observed experimentally, although some theoretical research indicates that it could be discovered at the LHC [10, 11].

Despite the lack of experimental evidence, theoretical investigations into the triply charmed baryon have been actively pursued using various approaches, including the quark model [12−18], QCD sum rules [19−21], Faddeev equations [22−24], the di-quark model [25, 26], the variational method [27, 28], the bag model [29, 30], Regge theory [31], and the Bethe-Salpeter equation [32]. These studies predict the mass of the ground state triply charmed baryon to be approximately 4.8 GeV. Numerous theoretical calculations have also been conducted to determine the mass spectrum under both quenched [33] and unquenched lattice QCD [34−44]. The predicted ground state mass from these lattice QCD calculations is consistent with other theoretical predictions.

Beyond spectroscopy, decomposing the mass of a hadron within the QCD framework offers deeper insights into its internal structure. This approach provides valuable information about the distribution of mass contributions from various components within the hadron. The mass decomposition of the nucleon was first proposed in [45], taking into account the dynamic interactions between quarks and gluons. In this framework, hadron mass is divided into four components: quark energy, quark mass, gluon energy, and trace anomaly. Mass decomposition has been explored in various hadronic systems, yielding novel insights [46−48]. For instance, it has been found that the trace anomaly contributes significantly in light hadron systems [46], and the quark mass matrix contributes less in hybrids compared to charmonium [48]. In this work, we aim to study the mass decomposition of the ground state triply charmed baryon using lattice QCD. We will first calculate the hadron mass M, the valence charm quark mass contribution $ \langle H_{m}\rangle $, and the valence charm quark momentum fraction $ \langle x\rangle_{q} $ using lattice QCD. Subsequently, the other components of the hadron mass can be determined through the decomposition formula of the QCD energy-momentum tensor (EMT) and the trace sum rule.

There is also a mass decomposition in the non-relativistic quark model, where the hadron mass is seperated into three parts: the mass and kinetic energy of the constituent quarks and the potential energy between them. The hyper-fine splitting is primarily attributed to the spin-spin interaction arising from the one-gluon exchange potential. Previous results for the heavy meson mass decomposition from lattice QCD appear to align with the perspective of the constituent quark model [46]. In this work, we also study the mass decomposition in the constituent quark model for comparison and attempt to gather clues of the correlation between the phenomenological model and QCD theory, which may deepen our understanding of their intrinsic nature. Because triply charmed baryons exist in an energy region where non-perturbative interactions cannot be ignored, a precise decomposition of the mass will provide valuable insights into comprehending the non-perturbative properties of QCD.

The remainder of our article is organized as follows: In Sec. II, we provide a detailed introduction to the hadron mass decomposition formula within the QCD framework. We also discuss the relationship between the hadron mass and two-point functions and between the hadron matrix elements and three-point functions. In Sec. III, we present details of our numerical simulations, including the configuration information, effective mass, effective matrix element calculations, and fitting results. In Sec. IV, we analyze and discuss our results, including comparisons with the constituent quark model. Finally, a brief summary is provided in Sec. V.

In this article, we adopt the QCD energy-momentum tensor decomposition proposed by Ji [45] used in Refs. [46−48]. The QCD energy-momentum tensor is written as

where () symmetrizes all the indices, $ \overleftrightarrow{D}^{\mu}=\overrightarrow{D}^{\mu}-\overleftarrow{D}^{\mu} $, $ \overrightarrow{D} $ is the gauge-covariant derivative, and $ F^{\mu\nu} $ is the color field strength tensor. The QCD Hamiltonian and the hadron mass could be written in terms of the energy-momentum tensor

where the hadron state $ |H\rangle $ is renormalized as $ \langle H|H\rangle= 2E(2\pi)^{3}\delta^{3}(0) $.

The hadron mass can be decomposed as

in the rest frame of the hadron state with

where $ \sum_{f} $ denotes the summation of quark flavors, $ \gamma_{m} $ is the quark mass anomalous dimension, and $ \beta(g) $ is the QCD β function. $ H_{E} $, $ H_{M} $, $ H_{g} $, and $ H_{a} $ denote contributions from the quark energy, quark condensate, gluon field energy, and joint contributions to quantum anomalies from gluons and quarks in Euclidean space, respectively. Both $ \langle H_{M}\rangle $ and $ \langle H_{a}\rangle $ are independent of scale and renormalization scheme. In contrast, the quark energy $ \langle H_{E}^{(\mu)}\rangle $ and gluon field energy $ \langle H_{g}^{(\mu)}\rangle $ are scale and renormalization dependent.

Thus, the renormalized quark and gluon energy are derived as

where $ \langle x\rangle_{q}^{R} $ and $ \langle x\rangle_{g}^{R} $ are the renormalized momentum fractions of quarks and gluons, respectively. These fractions satisfy the relation $ \langle x\rangle_{g}^{R}=1-\langle x\rangle_{q}^{R} $ [49]. Following Ref. [48], we could also define the total valence charm quark contribution as

In combination with the trace sum rule [50]

a component of the mass decomposition will be obtained through the calculation of the hadron mass M, the quark condensate contribution $ \langle H_{M}\rangle $, and the quark energy contribution $ \langle H_{E}\rangle $.

The components of the mass decomposition can be extracted from the corresponding two-point and three-point correlation functions. To construct the correlation function for the triply charmed baryon, similar to the Omega baryon [51], we use the operator for the triply charmed baryon as

where $ C=\gamma_{2}\gamma_{4} $ is the C-parity operator; α, β, γ represent the Dirac indices; a, b, and c are the color indices; and T is the transpose operator. To project onto a definite parity, we use the following parity projection operator:

Additionally, to project onto the triply charmed baryon with a definite spin, we use the following spin projection operators [52]:

In our study, only the spatial components of the triply charmed baryon operator are considered. Therefore, the baryon operator with a definite $ J^{P} $ quantum number can be expressed as

The hadron mass M can be obtained from the two-point correlation function

here, $ M_{0} $ represents the ground state hadron mass, and $ Z_{0} $ is the overlap matrix element between the ground state hadron and the hadron operator. Hadronic matrix elements, such as the quark content $ \langle H_{M}\rangle $ and the quark momentum fraction $ \langle x\rangle_{q} $, can be extracted from the three-point function

where $ J(\vec{y},t^{\prime}) $ refers to the current operator. Here, we only considered the contribution of the valence charm quark. For the quark content $ \langle H_{m}\rangle $, the corresponding current operator is

where $ m_{c} $ refers to the bare charm quark mass. For the charm quark momentum fraction $ \langle x\rangle_{q} $, the current operator is

In this calculation, we used the 2+1 flavor domain wall fermion and Iwasaki gauge action configurations provided by the RBC/UKQCD collaboration [53, 54]. Table 1 presents the parameters of these gauge ensembles. For the valence charm quark, we employ the overlap fermion with exact chiral symmetry on the lattice, which ensures that the valence charm quark mass matrix $ \langle H_{M}\rangle $ is independent of the renormalization scale and scheme [55]. The valence charm quark mass adopted in both ensembles follows the same tuning procedure as in Ref. [48], where the physical $ J/\psi $ mass was used as the matching criterion.

Ensemble	$ L^{3}\times T $	$a/\mathrm{fm}$	$m_{\pi}/\mathrm{MeV}$	$ m_{c}a $	$N_{\mathrm{cfg}} $
32I	$ 32^{3}\times64 $	$ 0.0828(3) $	300	0.493	305
48If	$ 48^{3}\times96 $	0.0711(3)	278	0.410	205

Table 1.  The parameters for the configurations [48].

To extract the hadron mass, we directly fit the two-point correlation function. Considering the unphysical oscillatory behavior introduced by the Domain Wall fermion [56], we use the following fitting function for the two-point function:

In this expression, ${\rm e}^{-\delta mt}$ is used to absorb the contributions from the excited states, and ${\rm e}^{-\widetilde{M}t}$ is the oscillating term. The parameters M, $ \delta m $, $ \widetilde{M} $, W, $ A_{0} $, and $ A_{1} $ are determined through the fitting process. This approach allows us to account for and mitigate the effects of oscillations in the data when determining the hadron mass.

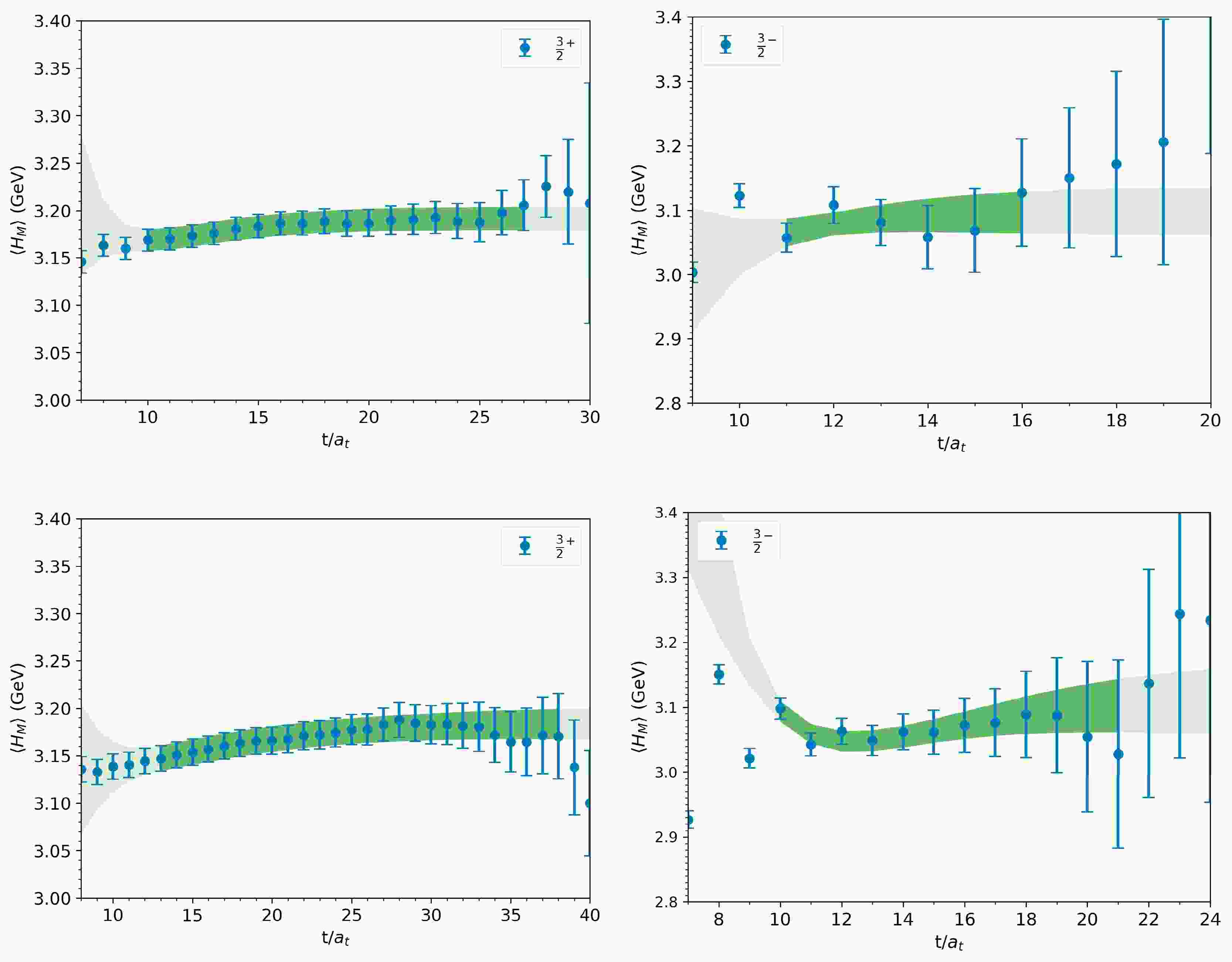
The effective masses of the two triply charmed baryons with quantum numbers $J^{P}= {3}/{2}^{+}$ and $J^{P}= {3}/{2}^{-}$ obtained from two different lattice configurations are depicted in Fig. 1. In the figure, the dark color bands represent our fitting range, while the light color bands indicate the extrapolation results. The fitted masses and $ \delta m $ of the two different triply charmed baryons are shown in Table 2. Because we have two lattice spacings and the results on the two ensembles are consistent within errors, we perform a constant extrapolation to obtain the results at the continuum limit.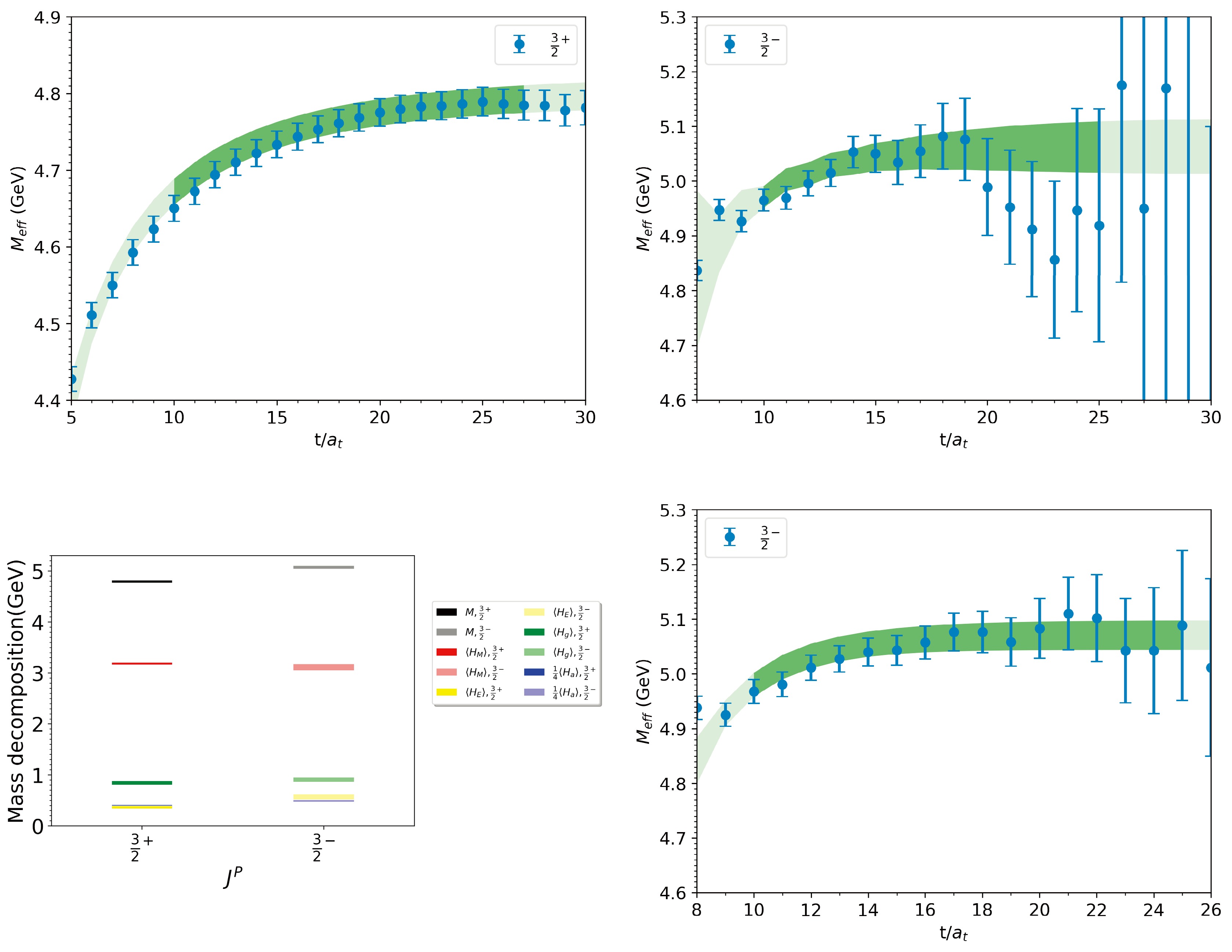

Figure 1.  (color online) Effective mass $ m_{{\rm eff}}={\rm ln}\left(\frac{C_{2}(t+1)}{C_{2}(t)}\right) $ for two triply charmed baryon states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations.

Ensemble	$ J^{P} $	M/GeV	$ \delta m $/GeV	$ [t_{\min}-t_{\max}] $	$\chi^{2}/{\rm{d.o.f}}$
32I	$ \frac{3}{2}^{+} $	4.804(20)	0.300(52)	10−27	0.76
	$ \frac{3}{2}^{-} $	5.064(51)	0.64(64)	10−25	1.4
48If	$ \frac{3}{2}^{+} $	4.793(21)	0.439(58)	13−38	0.42
	$ \frac{3}{2}^{-} $	5.071(27)	1.14(36)	10−25	0.85
$ \infty $	$ \frac{3}{2}^{+} $	4.799(14)
	$ \frac{3}{2}^{-} $	5.069(24)

Table 2.  The hadron mass for two triply charmed baryon states on $ 32^{3}\times64 $ (32I) and $ 48^{3}\times96 $ (48If) configurations along with the fitting range $[t_{\min}-t_{\max}]$ and $\chi^{2}/{\rm{d.o.f}}$. The results of constant extrapolation are also shown in the last row.

To obtain the charmness content $ \langle H_{M}\rangle $ and the charm quark momentum fraction $ \langle x\rangle_{q} $, we must calculate the corresponding three-point correlation functions. We employ the Feynman-Hellmann inspired method to compute the three-point function as done in Refs. [48, 57] and readers are referred to Ref. [58] for more details. The corresponding current-summed three-point function is given by

Here, the sum over c represents the various possible contractions of the current coupling to a quark propagator and $ G_{c}^{J} $ denotes the Feynman-Hellmann propagator

Γ represents the product of the initial and final state γ matrices. For simplicity, the contraction over color indices is omitted. II, III, and IV denote the contributions from the regions of $ t<t'<T $, $ t'=0 $, and $ t'=t $, respectively, and they are absorbed in the $ d_{n} $ term despite a ${\rm e}^{-E_{n}t}$ factor. $ Z_{n} $ represents the overlap factor. $ J_{nn} $ denotes the hadronic matrix element. $ \Delta_{nm} $ is defined as $ \Delta_{nm}\equiv E_{m}-E_{n} $.

The ratio of the three-point function to the corresponding two-point function is defined as

In the second step, we assume that $ C^{(2)}(t) $ is primarily contributed by the ground state and incorporate some of the coefficients related to the excited states into $ C_n $ and $ D_n $ for simplicity. We can derive the matrix element $ J_{00} $ from the derivative of R(t)

Although the subtraction procedure may introduce larger relative statistical uncertainties, it efficiently generates results for multiple all sink times. It avoids the computational cost of repeatedly calculating propagators for each sink time (as in traditional sink-sequential approaches). The increased data density across time separations improves the control of excited-state contamination and enhances the accuracy of extracting the desired hadronic matrix elements. The lattice correlator with all sink times available improves the control of excited-state contamination (at sink) and thus the extraction of the desired matrix elements. The final numerical results are all of decent precision.

The effective hadronic matrix elements can be obtained from the difference of R(t) as

Then, the hadronic matrix elements $ \langle H_{M}\rangle $ and $ M\langle x_{q}\rangle $ can be fitted using the formulas as

where $ \delta m $, $ H_M $, $ x_q $, $A_{1}^{\prime},~A_{2}^{\prime},~A_{3}^{\prime},$ and $ A_{4}^{\prime} $ are fitting parameters, and the exponential terms are used to absorb the contribution from excited states.

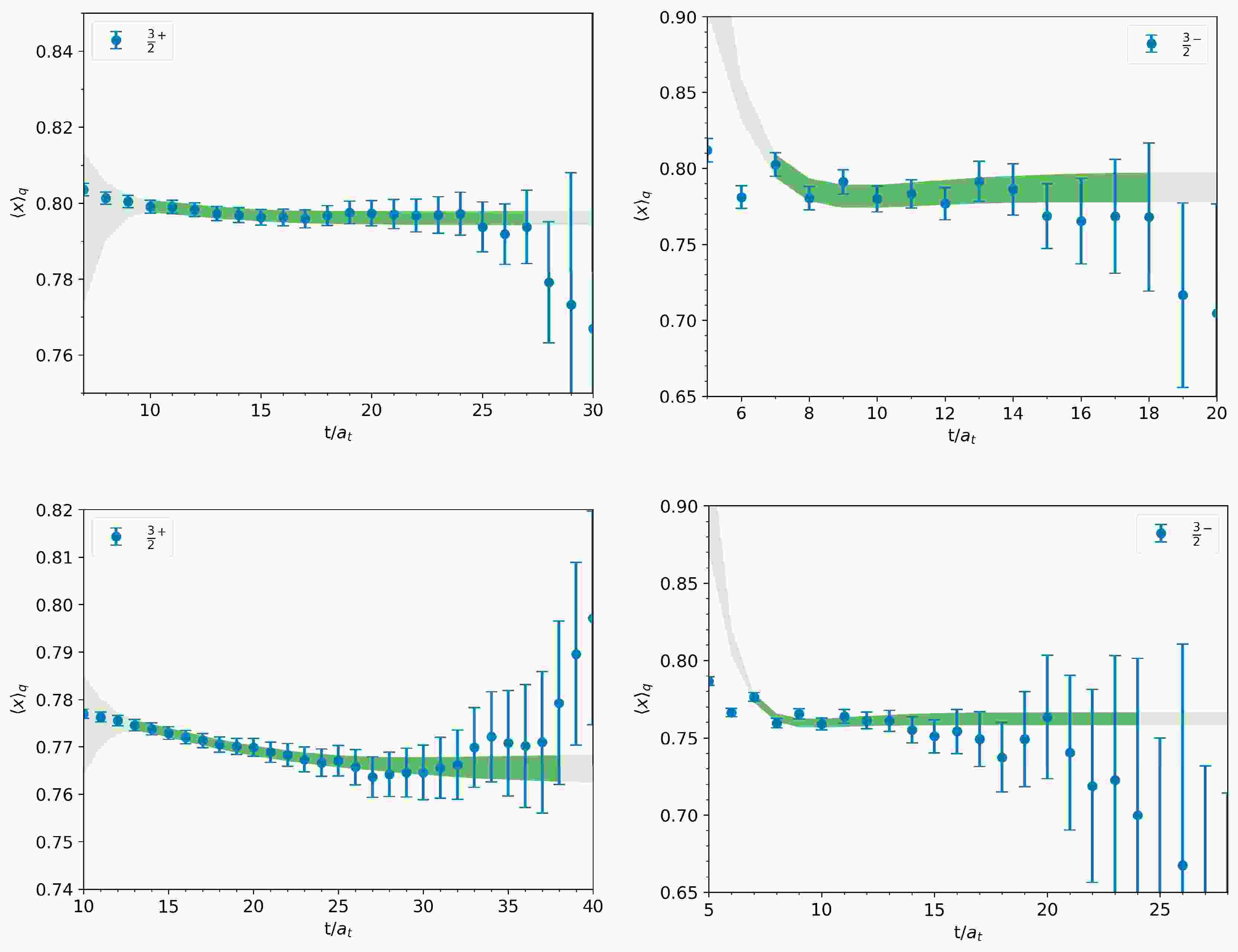
The fitting of the effective matrix elements of the charmness content $ \langle H_{M}\rangle $ and the valence charmed quark momentum fraction $ \langle x\rangle_{q} $ are shown in Fig. 2 and Fig. 3, respectively. The dark color bands represent our fitting range, while the light color bands show the extrapolation results. The fitted results of the corresponding hadron matrix elements are shown in Table 3 and Table 4. Our results reveal that, on two different configurations, the charmness content of the orbital excited state ${3}/{2}^{-}$ is slightly smaller than that of the ground state ${3}/{2}^{+}$.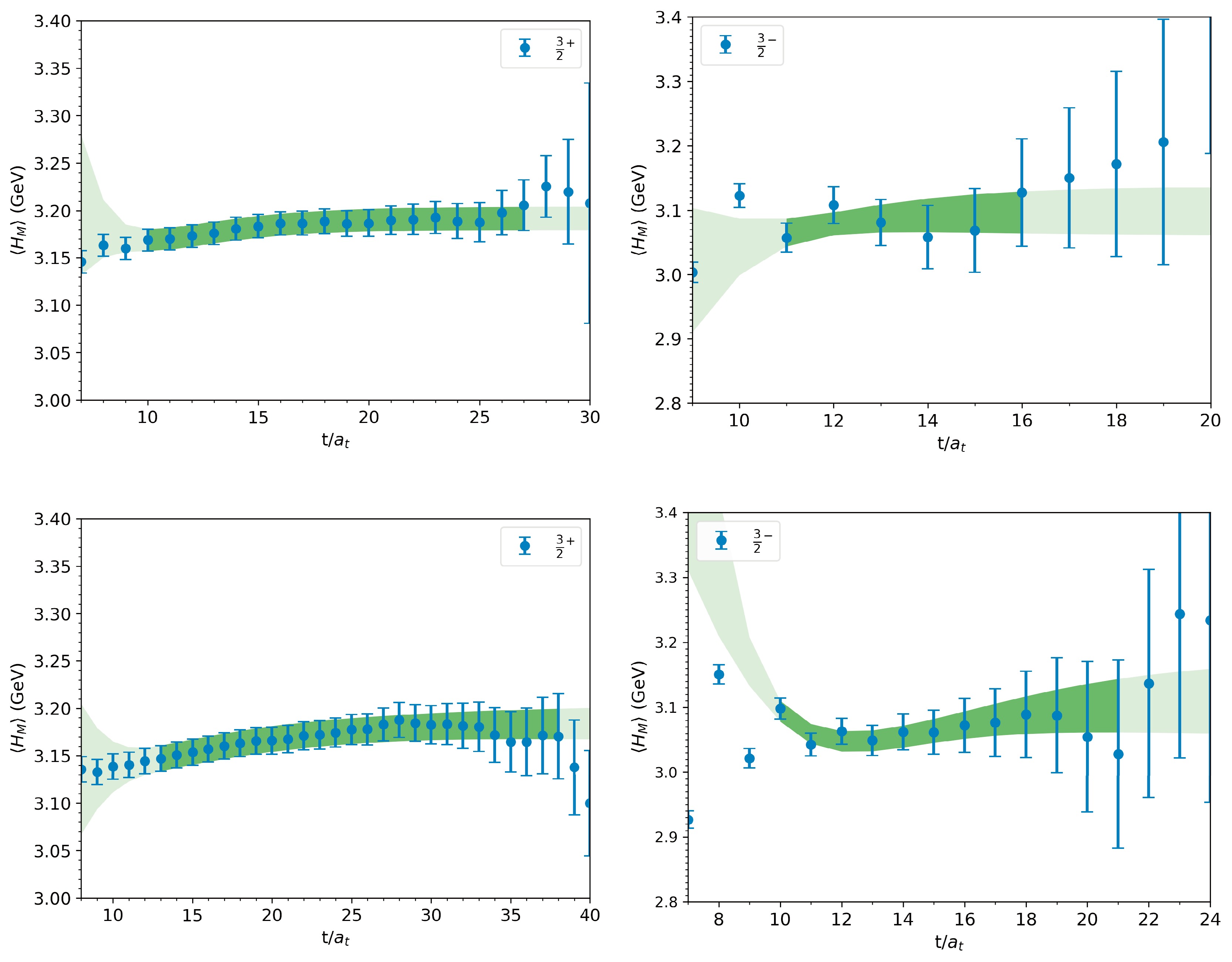

Figure 2.  (color online) Effective matrix elements of the charmness content $ \langle H_{M}\rangle $ for two triply charmed baryon states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations.

Figure 3.  (color online) Effective matrix elements of valence charmed quark momentum fraction $ \langle x\rangle_{q} $ for two triply charmed baryon states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations.

Ensemble	$ J^{P} $	$ \langle H_{M}\rangle $/GeV	$ [t_{\min}-t_{\max}] $	$\chi^{2}/{\rm{d.o.f}}$
32I	$ \frac{3}{2}^{+} $	3.192(13)	10−27	0.062
	$ \frac{3}{2}^{-} $	3.098(38)	11−16	0.38
48If	$ \frac{3}{2}^{+} $	3.185(19)	13−38	0.089
	$ \frac{3}{2}^{-} $	3.114(60)	10−21	0.33

Table 3.  The charmness content $ \langle H_{M}\rangle $ for two triply charmed baryon states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations along with the corresponding fitting range $[t_{\min}-t_{\max}]$ and $\chi^{2}/{\rm{d.o.f}}$.

Ensemble	$ J^{P} $	$ \langle x\rangle_{q} $	$[t_{\min}-t_{\max}]$	$\chi^{2}/{\rm{d.o.f}}$
32I	$ \frac{3}{2}^{+} $	0.7960(18)	10−27	0.096
	$ \frac{3}{2}^{-} $	0.7878(99)	7−18	1.7
48If	$ \frac{3}{2}^{+} $	0.7653(33)	13−38	0.12
	$ \frac{3}{2}^{-} $	0.7623(42)	7−24	1.1

Table 4.  The charmed quark momentum fraction $ \langle x\rangle_{q} $ for two triply states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations along with the corresponding fitting range $[t_{\min}-t_{\max}]$ and $\chi^{2}/{\rm{d.o.f}}$.

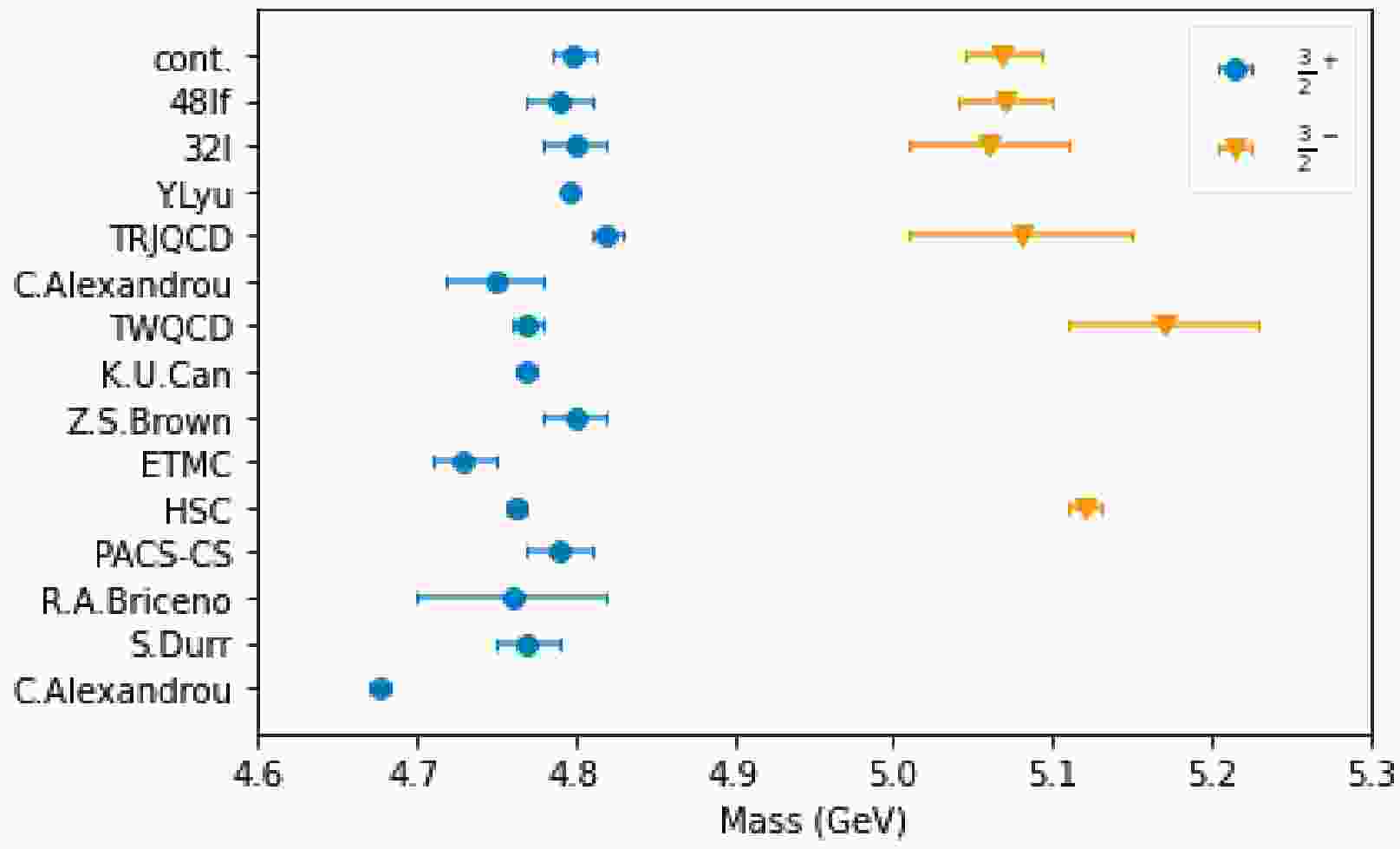
Before delving into the mass decomposition of the triply charmed baryon, we first briefly review and discuss the mass spectrum. Numerous lattice QCD studies have been conducted on the spectrum, and we have compiled their results alongside ours in Table 5, which are also presented more intuitively in Fig. 4. Regarding the ground ${3}/{2}^{+}$ state, most of the results are in good agreement. The result of Ref. [42] is as low as 4.6769(46)(30). However, the result is updated to 4.746(4)(32) when simulations were performed on configurations with the physical pion mass in Ref. [41]. Our results for the ${3}/{2}^{+}$ state are consistent with the other lattice calculations within error bars. For the p-wave ${3}/{2}^{-}$ state, the corresponding lattice calculations are fewer, and the uncertainties are relatively larger. Our results align closely with those of the TRJQCD collaboration but are slightly smaller than the results from the HSC and TWQCD collaborations. Considering that TRJQCD performed simulations on configurations close to the physical pion mass, the results we obtained here appear reasonable. After our work, two recent studies have also calculated the masses of the triply charmed baryon [59, 60]. In summary, the mass spectrum we obtained is consistent with other lattice calculations, indicating the reliability of our results within current computational constraints.

Collaboration	$ N_{f} $	$a/{\rm fm}$	$m_{\pi}/{\rm GeV}$	$S_{q}^{\rm sea}$	$S_{c}^{\rm val}$	$\Omega_{ccc}(\frac{3}{2}^{+})/{\rm GeV}$	$\Omega_{ccc}(\frac{3}{2}^{-})/{\rm GeV}$
[Ours]48If	2+1	0.0711(3)	0.278	Domain-wall	Overlap	4.793(21)	5.071(27)
[Ours]32I	2+1	0.0828(3)	0.3	Domain-wall	Overlap	4.804(20)	5.064(51)
[Ours]continuum	2+1					4.799(14)	5.069(24)
Y.Lyu et al. [61]	2+1	0.0846	0.146	Wilson	RHQA	4.7956(7)
TRJQCD [40]	2+1	0.0907(13)	0.156(9)	Clover	Clover	4.817(12)	5.083(67)
C.Alexandrou et al. [41]	2	0.0938(3)(2)	0.130	Twisted Mass	OS	4.746(4)(32)	−
TWQCD [44]	2+1+1	0.063	0.280	Domain-wall	Domain-wall	4.766(5)(11)	5.168(37)(51)
K.U.Can [38]	2+1	0.0907(13)	0.156(7)(2)	Wilson	Clover	4.769(6)	−
Z.S.Brown et al. [37]	2+1	0.085−0.11	0.227−0.419	Domain-wall	RHQA	4.796(8)(18)	−
ETMC [39]	2+1+1	0.065−0.094	0.210−0.430	Twisted Mass	Twisted Mass	4.734(12)(11)(9)	−
HSC [36]	2+1	0.0351(2)	0.390	Clover	Clover	4.763(6)	5.124(13)
PACS-CS [35]	2+1	0.0899	0.135(6)	Clover	RHQA	4.789(22)	−
R.A.Briceno et al. [34]	2+1+1	0.06−0.12	0.220−0.310	HISQ	RHQA	4.761(52)(21)(6)	−
S.Durr et al. [43]	2	0.0728(5)(19)	0.280	Wilson	Brillouin	4.774(24)	−
C.Alexandrou et al. [42]	2	0.0561(1)−0.089(1)	0.260−0.450	Twisted Mass	OS	4.6769(46)(30)	−

Table 5.  The masses of the ground state $ \Omega_{ccc}(1^{4}S_{3/2^{+}}) $ and the orbital excited state $ \Omega_{ccc}(1^{2}P_{3/2^{-}}) $we calculated on $ 32^{3}\times64 $ (48If) and $ 48^{3}\times96 $ (32I) configurations are shown alongside the results from other lattice QCD collaborations. The corresponding flavor number ($ N_{f} $), lattice spacings (a), pion mass ($ m_{\pi} $), actions of relevant sea ($S_{q}^{\rm sea}$), and valence charm ($S_{c}^{\rm val}$) quarks are included for comparison. The abbreviations HISQ and RHQA stand for highly-improved staggered quark and relativistic heavy-quark action, respectively.

Figure 4.  (color online) Masses of ${3}/{2}^{+}$ and ${3}/{2}^{-}$ triply charmed baryons on lattice QCD.

This study neglected the sea charm quark mass term $ \langle H_{M}^{c,\text{sea}}\rangle $ for calculation convenience. This is a reasonable approximation since$ \langle H_{M}^{c,\text{sea}}\rangle $ is estimated to be less than 100 MeV for both ${3}/{2}^{+}$ and ${3}/{2}^{-}$ states on each lattice ensemble based on the heavy quark expansion [50]:

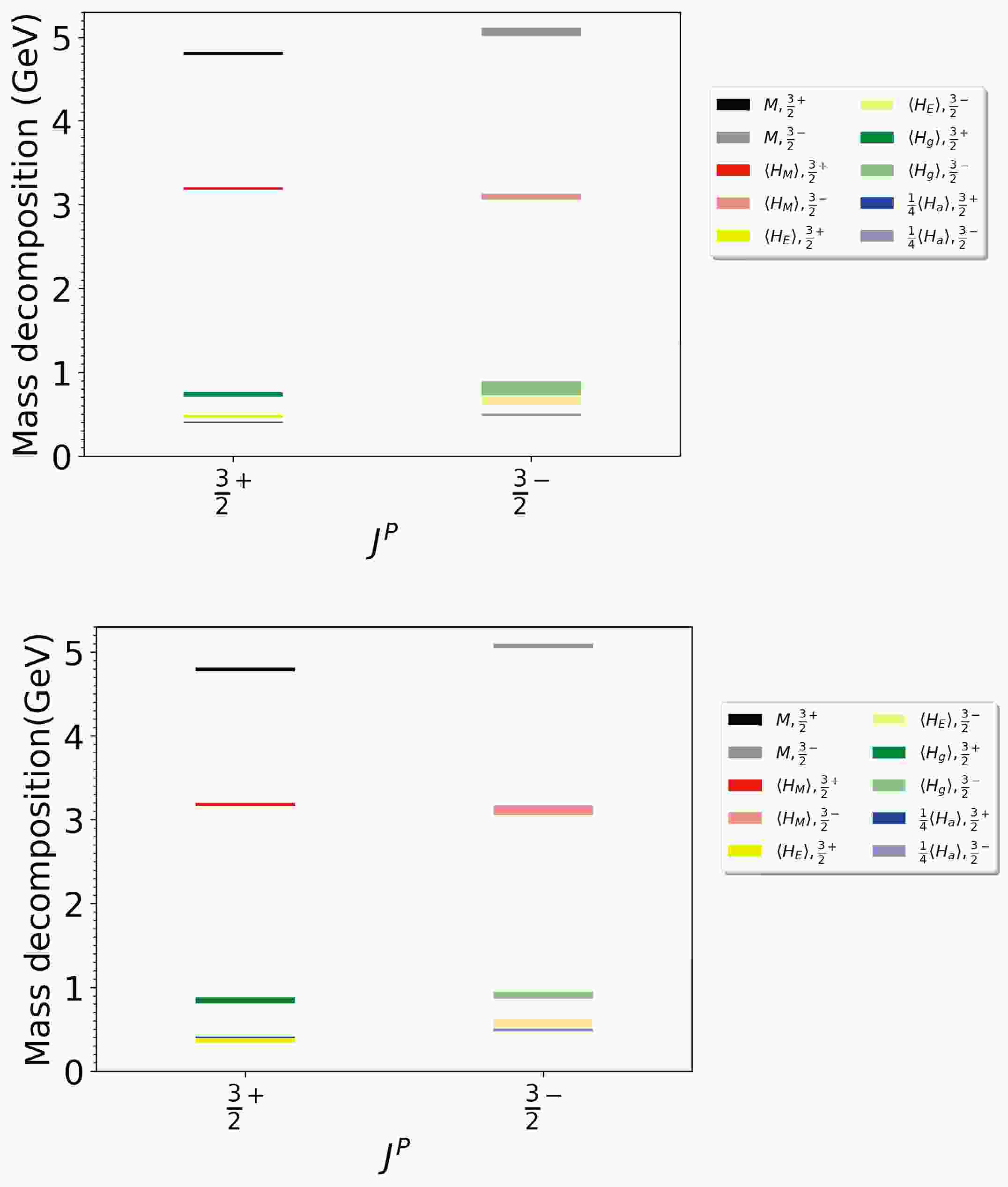
Here, $ \gamma_{m}(\mu)\approx\dfrac{2\alpha(\mu)}{\pi} $ is the quark anomalous dimension and $ \alpha(\mu=m_{c})\approx0.37 $ is taken from Ref. [62]. As to the light and strange sea quarks, we conjecture that it is also safe to neglect their contributions, based on the observation that their total contribution is less than 40 MeV in charmonium [48]. Disconnected diagrams are also not considered, so their contribution is absorbed in the QCD anomaly term $ H_{a} $ and the gluon energy term $ H_{g} $. Possibly this is the reason why the values of $ H_{a} $ and $ H_{g} $ we obtained in the triply charmed baryon are slightly larger than those in charmonium states, as shown in Table 6 and more intuitively illustrated in Fig. 5. Nevertheless, the total valence charm quark contribution $ H_{q} $ remains the main contributor to the triply charmed baryon mass, accounting for approximately 75% of the total mass. This is consistent with the pattern observed in charmonium but differs from that in light baryons, where the trace anomaly contribution is more significant.

$ J^{P} $	$M /{\rm{GeV} }$	$\langle H_{M}\rangle /{\rm{GeV} }$	$\langle H_{E}\rangle /{\rm{GeV} }$	$\langle H_{g}\rangle /{\rm{GeV} }$	$\dfrac{1}{4}\langle H_{a}\rangle /{\rm{GeV} }$	$ \mathcal{M}_{S} $
$ \frac{3}{2}^{+} $	4.804(20)	3.192(13)	0.474(17)	0.735(30)	0.403(06)	2.742(46)
$ \frac{3}{2}^{-} $	5.064(51)	3.098(38)	0.669(56)	0.806(86)	0.492(16)	2.661(54)
$ J/\psi $	3.104(02)	2.162(02)	0.264(03)	0.442(02)	0.2355(07)	1.857(30)
$ \chi_{c1} $	3.434(11)	2.101(30)	0.335(37)	0.664(28)	0.333(08)	1.805(39)
$ \frac{3}{2}^{+} $	4.793(21)	3.185(19)	0.362(22)	0.844(37)	0.402(07)	2.822(76)
$ \frac{3}{2}^{-} $	5.071(27)	3.114(60)	0.564(50)	0.904(84)	0.489(16)	2.759(90)
$ J/\psi $	3.100(01)	2.139(01)	0.2116(25)	0.509(02)	0.2403(04)	1.895(50)
$ \chi_{c1} $	3.480(18)	2.063(38)	0.387(47)	0.676(37)	0.354(11)	1.828(58)

Table 6.  Mass decomposition of ${3}/{2}^{+}$ and ${3}/{2}^{-}$ triply charmed baryon states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations, along with the mass decomposition of charmonium states. The charmness matrix element $ \mathcal{M}_{s} $ are also listed for comparison.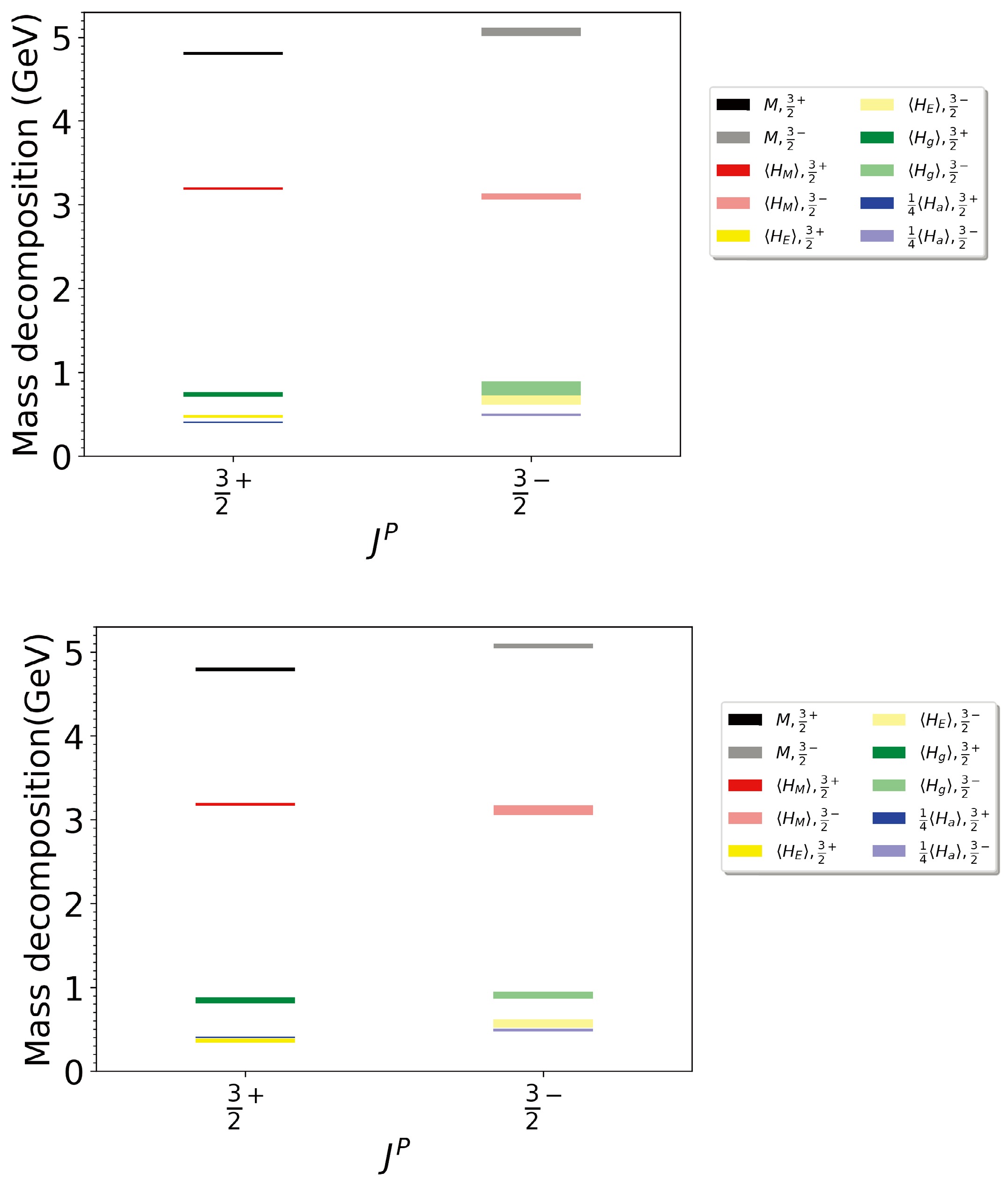

Figure 5.  (color online) Mass decomposition for of ${3}/{2}^{+}$ and ${3}/{2}^{-}$ triply charmed baryon states on $ 32^{3}\times64 $ (top) and $ 48^{3}\times96 $ (bottom) configurations.

The quark mass contribution $ H_{M} $ in the triply charmed baryon is about ${3}/{2}$ times that in charmonium. This is consistent with the scenario where a baryon is composed of three valence quarks while a meson is composed of two. In fact, the quark condensate contribution is similar to the well-known sigma term in nucleon physics. Following the definition of the sigma term, we define the renormalized charmness matrix element in the triply charmed baryon as

where $ Z_{S} $ is the renormalization constant of the scalar current. As done in Refs. [63, 64], we adopt $ Z_{S}= $ [1.009(16), 1.008(26)] for the ensembles of 32I and 48If, respectively. The charmness matrix element for the triply charmed baryon ${3}/{2}^{+}$ and ${3}/{2}^{-}$ states are obtained as shown in Table 6, where they are shown alongside those of the charmonium. The charmness matrix elements in triply charmed baryons are greater than those in charmonium. This difference arises primarily because the scalar current operator couples to the triply charmed baryon with a factor of 3, whereas the corresponding factor for charmonium is 2. If the effects of these factors are removed, the relation $ \dfrac{1}{3}\mathcal{M}_{S}(\Omega)\sim \dfrac{1}{2}\mathcal{M}_{S}(\bar{c}c)\sim 0.9 $ is obtained.

Moreover, the mass decomposition provides insights into the nature of the mass splitting between s-wave (${3}/{2}^{+}$) and the p-wave (${3}/{2}^{-}$) states. Our calculations indicate a mass splitting of approximately 250 MeV, with the primary contribution stemming from the quark energy term at around 200 MeV. In contrast, the contributions from the QCD anomaly term $ H_{a} $ and the gluon energy term $ H_{g} $ are each less than 100 MeV. This differs from the scenario in charmonium, where the contributions of $ H_{g} $ and $ H_{a} $ are comparable to that of $ H_{E} $, as shown in the charmonium mass decompositions in Table 6. For comparison, we have also calculated the rest energy composition of the ground state (${3}/{2}^{+}$) and orbitally excited state (${3}/{2}^{-}$) triply charmed baryons within the framework of the constituent quark model. Following Ref. [16], the Hamiltonian for the triply charmed baryon can be expressed as

where $ M_{q} $ and T denote the mass and kinetic energy of the constituent quarks, respectively. $ V^{C}_{ij} $ is the confinement potential defined as $V_{i j}^{C}=\dfrac{b}{2} r_{i j}$. $ V^{G}_{ij} $ is the one-gluon exchange potential, and the explicit expression along with the quantities involved are written as follows:

Here, $ S_i $, S, and L are the spin operator of the i-th quark, the total spin of the baryon, and the total orbital angular momentum of the baryon, respectively. b, $ \alpha_{ij} $, and $ \alpha_{\mathrm{SO}} $ denote the strength of confinement potential, strong coupling, and spin-orbit potential. The same parameters are adopted as in Ref. [16]. The corresponding mass decomposition with explicit values of $M_{q},\; T,\; V^{C}, \; V^{\rm coul}, \; V^{SS}, V^{T}$ ,and $ V^{SL} $ for both the ${3}/{2}^{+}$ and ${3}/{2}^{-}$ states are derived as shown in Table 7.

$ J^{P} $	$ M $	$ M_{q} $	$ T $	$ V^{C} $	$V^{\rm coul}$	$ V^{SS} $	$ V^{LS} $
$ \frac{3}{2}^{+} $	4828	4450	533	471	−647	21	0
$ \frac{3}{2}^{-} $	5162	4450	538	630	−466	4	7

Table 7.  Mass decomposition in the quark model. $ M $ is the hadron mass of a triply charmed baryon. $ M_q $ represents the quark mass term, $ T $ denotes the kinetic energy term, $ V^C $ stands for the confinement potential, $V^{\rm coul}$ is the Coulomb potential, $ V^{SS} $ refers to the spin-spin potential, and $ V^{LS} $ is the spin-orbit potential. The tensor potential $ V^{T} $ is zero in both of these states and has therefore been excluded. The data are given in MeV.

The constituent quark mass terms for the ${3}/{2}^{+}$ and ${3}/{2}^{-}$ states are identical, each being three times the constituent quark mass. Notice that the constituent quark mass is input as a constant, and the kinetic energy terms are similar for both states. The mass difference between the ${3}/{2}^{+}$ and ${3}/{2}^{-}$ states primarily arises from the potential energy terms $ V^{C} $ and $ V^{G} $. The influences of these two potential terms act in opposite directions. The confinement potential $ V^{C} $ has a constructive effect on hadron mass, while the one-gluon exchange potential $ V^{G} $ exerts a destructive influence. The ${3}/{2}^{-}$ state has a stronger confinement potential coupled with a weaker one-gluon exchange potential, leading to a slightly higher mass compared to the ${3}/{2}^{+}$ state, which is consistent with lattice QCD calculations.

It is quite complicated to directly relate lattice QCD to phenomenological models. However, under certain limits, quantities defined in lattice QCD can reflect phenomenological insights. For example, the gluon trace anomaly term $ \langle H_{a}^{g} \rangle $ for a heavy quark-antiquark pair system is related to the confinement potential by

in the heavy quark limit, as demonstrated in Refs. [65, 66]. Here, A is a constant and $ V(r) = \sigma r $ is the confinement potential. One may wonder whether this relation still holds for triply charmed baryons. In our calculation, the gluon trace anomaly term $\langle H_{a}^{g}\rangle_{H} =\langle\frac{\beta}{2g}\int {\rm d}^{3}\vec{x}G^{2}\rangle_{H}$ can be deduced from

where $ \langle H_{a}^{q}\rangle_{H} =\gamma_{m}\langle H_{m}\rangle_{H} $ denotes the quark trace anomaly term. Here, we focus on the difference in $ \langle H_{a}^{g}\rangle_{H} $ for the ${3}/{2}^{+}$ and ${3}/{2}^{-}$ states to eliminate the effect of the unknown constant A. Adopting $ \gamma_{m} = 0.295 $ from Ref. [60], we find that the difference of the gluon trace anomaly term is $ \Delta\langle H_{a}^{g}\rangle_{\Omega_{ccc}} \equiv\langle H_{a}^{g} \rangle_{\frac{3}{2}^{-}} - \langle H_{a}^{g} \rangle_{\frac{3}{2}^{+}} = 0.384(69)_{\text{32I}}\, \text{GeV or } 0.369(72)_{\text{48IF}} $ GeV. In comparison, the corresponding difference of the confinement potential in the quark model is $ \Delta V^{C}(r)\equiv V^{C}(r)_{\frac{3}{2}^{-}}-V^{C}(r)_{\frac{3}{2}^{+}} \simeq 0.16 $ GeV. This approximately satisfies the relation $ \Delta\langle H_{a}^{g}\rangle_{\Omega_{ccc}} \simeq 2\Delta \langle V^{C} \rangle $, which is consistent with the charmonium case in the heavy quark limit as denoted by Eq. (35). It implies that there may be a connection between the trace anomaly and hadron confinement. Further studies on this issue would be beneficial.

This study investigated the mass decomposition of triply charmed baryons within the lattice QCD framework. The two lowest triply charmed baryons were calculated on two lattice ensembles, and an appropriate mass spectrum that was consistant with other calculations was obtained. The mass decompositions of both ${3}/{2}^{+}$ and ${3}/{2}^{-}$ triply charmed baryon states on two lattices were obtained. We found that the total valence charm quark contribution $ H_{q} $ is dominant in triply charmed baryon, which is consistent with the pattern observed in charmonium but differs from that displayed in nucleons, where the trace anomaly contribution plays a major role.

We also calculated the mass decomposition of these two states in the constituent quark model. It is challenging to directly correlate the mass components decomposed on lattice QCD with those in the quark model. Nevertheless, an analysis of the gluon trace anomaly in triply charmed baryons demonstrated a relation with the confinement potential analogous to that of the heavy quark-antiquark system. This implies a possible connection between the trace anomaly and the confinement potential.

The authors L. C. Gui, W. Sun and J. Liang, as memebers of the χQCD corllaboration, thank the RBC collaboration for providing us their DWF gauge configurations. We thank Hui-hua Zhong for useful discussion. The computations were performed on the Xiangjiang-1 cluster at Hunan Normal University (Changsha) and the Southern Nuclear Science Computing Center (SNSC) and the HPC clusters at Institute of High Energy Physics (Beijing) and China Spallation Neutron Source (Dongguan) and the ORISE Supercomputer.