Sub-barrier fusion analysis of ⁴⁰Ca + ^46,48,50Ti systems

The sub-barrier fusion process proceeds via quantum-mechanical tunnelling due to the wave nature of colliding systems and projectiles penetrating through the nominal barrier and fusing into the potential pocket formed between projectile-target systems. This results in the formation of a compound nucleus that, after equilibration, further leads to the final product. The one-dimensional barrier penetration model (BPM) has been widely used to predict fusion yields and for analysis of the behaviours of heavy-ion fusion cross-sections around the Coulomb barrier. This model assumes that incoming flux that passes through the nominal barrier contributes to the fusion process. The fusion reaction around Coulomb barrier was extensively studied in the field of heavy-ion interactions. In the literature, numerous experiments as well as theoretical investigations were performed in past couple of decades, with many heavy-ion fusing systems [1−7]. Researchers in the field of heavy-ion fusion dynamics were stimulated by the recognition that sub-barrier fusion cross-sections were found to be enhanced by many orders of magnitude over what would be expected from one-dimensional BPM. This enhancement was attributed to the involvement of intrinsic degrees of freedom associated with the collision partners during the fusion process. In the literature [8−15], numerous attempts have been made to identify the cause of sub-barrier fusion enhancement as well as the effects of intrinsic degrees of freedom associated with fusing nuclei on fusion dynamics. However, this appears to be a complex problem for heavy-ion fusion dynamics. The static and dynamic deformation of the projectile (or target or both), zero-point motion of the nuclear surface, and nucleon transfer channels were pointed out as dominant intrinsic degrees of freedom, and their involvement leads to anomalously larger sub-barrier fusion enhancement relative to the outputs of the one-dimensional BPM, as observed for many heavy-ion fusion reactions.

In addition to the aforementioned channel coupling effects, the choice of nucleus-nucleus interaction potential between colliding nuclei is very crucial for theoretical estimations of fusion cross-sections. Processes like elastic and inelastic scattering are very sensitive to the surface part of the nucleus-nucleus potential, while fusion reactions are sensitive to the internal part of the nucleus-nucleus potential [16−19]. In this regard, the knowledge of nucleus-nucleus potential is helpful in describing heavy-ion fusion dynamics. The Coulomb and centrifugal-potential terms of total nucleus-nucleus interaction potential are well understood. However, there are considerably large ambiguities in the radial dependence of the nuclear potential term; hence, many different parameterizations of nuclear potential have been used [13, 15, 18−21, 22−35]. The Woods-Saxon form has been widely used for exploration of nuclear reaction dynamics. In heavy-ion fusion dynamics, one of most challenging issues for such nuclear potential is the diffuseness anomaly [18−19]. It has been demonstrated [18−19] that larger diffuseness parameter (${a_0} = 0.75~{\rm fm}\,\,{\text{to}}\,\,1.50\,{\rm fm}$) is certainly required for sufficient interpretation of fusion dynamics. This range of diffuseness is comparatively larger than a typical value (${a_0} = 0.65\,{\rm fm}$) that is frequently used for exploring elastic scattering data. Theoretically, all channel coupling effects, which are important for fusion enhancement, are considered via nucleus-nucleus potential, and this coupling results in splitting of the nominal fusion barrier into a number of barriers with distinct heights and weights. Such a group of barriers is named the barrier distribution and ultimately leads to large fusion enhancement over the expectations of one-dimensional BPM at near- and below-barrier energies. The influences of low-lying vibrational states like 2⁺ and 3^– associated with the projectile (or target) are more clearly visible for spherical nuclei, and the role of the neutron transfer channel is more puzzling in comparison to the effects of low-lying vibrational states related to nuclear structures of participants. The distinction between the effects of vibrational states and neutron transfer channel can be made if a common projectile is incident on a series of target isotopes, or vice-versa. In general, the probability of a multi-neutron transfer channel increases with increased neutron richness in the target, further resulting in enhanced cross-sections. The target (or projectile) isotopic dependence of fusion cross-section data appeared due to increased possibility of a neutron transfer channel that can be correlated with the neutron richness of the given target (or projectile) nucleus. The aim of the present work is to analyze the importance of neutron transfer channels and collective rapid variation of low-lying vibrational states of interacting nuclei. For such analysis, the fusion dynamics of ⁴⁰Ca + ^46,48,50Ti reactions is of great interest. The attractive feature of ⁴⁰Ca + ^46,48,50Ti [36] reactions is that target isotopes offer opposite mass dependence of collectivity of vibrational states and neutron transfer channels with positive Q-value. Due to large coupling strength and deformation for octupole vibration in the projectile (⁴⁰Ca), it displays strong octupole vibrational coupling, and its influences are supposed to be more pronounced than other inelastic surface excitations. The target isotopes (^46,48,50Ti) also exhibit vibrational spectra, and for selected reactions, the dominant mode of couplings is vibrational coupling, which is a major factor in the verification of low-energy-dependent fusion data. The neutron transfer couplings for neutron-rich nuclei are expected to have more influence relative to vibrational couplings; thus, with a given projectile, strong isotopic fusion enhancement is evident for a ⁵⁰Ti target isotope relative to spherical target isotopes ^46,48Ti.

The present work explores the fusion dynamics of ⁴⁰Ca + ^46,48,50Ti reactions within the preview of the simple Wong formula [37], simple Wong formula with deformed choice of nuclear potential [38−42], SAGBD model [43−48], and coupled channel formalism [49]. The predictions of simple Wong formula with no coupling calculations fail to provide a complete explanation of fusion data in below-barrier energy. To address the fusion dynamics of ⁴⁰Ca+^46,48,50Ti reactions, the theoretical estimations are performed using the Wong formula with deformed choice of the nuclear potential, which is referred to as the deformed Wong model. In this case, the effects of quadrupole deformation (${\beta _2}$) are included through deformed nuclear potential, and the results also remain underestimated relative to the experimental data, especially in sub-barrier energy regions. To improve the results, an additional radius parameter $\Delta R$ is used in the deformed Wong model, and with given $\Delta R$, the deformed Wong model reasonably explains the fusion data of given reactions. In the SAGBD model [43−48], the Wong formula is weighted by Gaussian function, and total fusion cross-sections are estimated by this weighted Wong formula. The influences of numerous favoured channels for sub-barrier fusion enhancement are entered in calculations via nuclear potential in coupled channel formalism and now in the SAGBD model are incorporated using a Gaussian weight function. The Gaussian function empirically considers the commulative effects of all dominant channels of collision partners. As a result, the total interaction barrier is modified, and the SAGBD-based outcomes reasonably explain the experimental fusion data and related barrier distribution data. In addition, SAGBD calculations with Winther [24] and Akyüz-Winther [25] diffuseness are performed, and it is found that the magnitude of fusion cross-sections is greater relative to the output of one-dimensional BPM but unable to address the experimental data. For an explanation of the experimental data of ⁴⁰Ca+^46,48,50Ti reactions, the diffuseness of chosen potential is optimized relative to the value of Winther and Akyüz-Winther diffuseness. Using such an optimal diffuseness parameter, the SAGBD model-based calculations explain the fusion data of given reactions well. In the SAGBD model, the contributions from favoured channels that are accountable for enhancement in fusion cross-sections are described in terms of channel coupling parameter $({\lambda ^{\rm SAGBD}})$ and percentage reduction in the effective fusion barrier relative to uncoupled Coulomb barrier (${V_{\rm CBRED}}$). In other words, ${\lambda ^{\rm SAGBD}}$, which quantitatively measures the role of dominant intrinsic channels, is responsible for enhancement in fusion process. Additionally, ${V_{\rm CBRED}}$ determines the quantitative reduction of fusion barrier due to the involvement of various channel coupling effects. The non-zero values of ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$ highlight the involvement of intrinsic degrees of freedom during the fusion process. The values of ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$ for ⁴⁰Ca+^46,48,50Ti reactions are extracted for the SAGBD calculations with an optimal diffuseness (${\lambda ^{\rm SAGBD}} = 3.38$, ${V_{\rm CBRED}}$=5.51% of ${V_{CB}}$ for ⁴⁰Ca + ⁴⁶Ti, ${\lambda ^{\rm SAGBD}} = 3.443.44$, ${V_{\rm CBRED}} = 5.62{\text{%}}$ of ${V_{CB}}$ for ⁴⁰Ca + ⁴⁸Ti, and ${\lambda ^{\rm SAGBD}} = 3.46$, ${V_{\rm CBRED}} = 5.73{\text{%}}$ of ${V_{CB}}$ for ⁴⁰Ca + ⁵⁰Ti). These results suggest that there is an isotopic target dependence of sub-barrier fusion enhancement. This clearly reveals the superiority of neutron transfer couplings over vibrational couplings with increased neutron richness in target isotopes. Further, entrance channel mass asymmetry $(\eta )$ is also seen to follow an increasing trend with increasing neutron richness in target isotopes.

To assess the pertinence of the SAGBD model, the fusion dynamics of ⁴⁰Ca + ^46,48,50Ti reactions have also been examined by adapting the coupled channel approach. The influences of multiphonon excitations of the nuclear surfaces like 2⁺ and 3^– vibrational states of participants are investigated using coupled channel calculations. For the studied reactions, the couplings to 2⁺ and 3^– vibrational states of both fusing pairs are found to be sufficient to address the observed fusion data of ⁴⁰Ca+^46,48,50Ti reactions. The 3^– vibrational states of the projectile are seen to be strong and dominant among other inelastic surface excitations, but they contribute equally with all target isotopes. Therefore, target isotopic sub-barrier fusion enhancement of ⁴⁰Ca + ^46,48,50Ti reactions emerged as a consequence of participation of low-lying vibrational excitations of Ti-isotopes. Furthermore, for ⁴⁰Ca + ⁵⁰Ti reactions, in addition to low-lying 2⁺ and 3^– vibrational states of projectile and target nuclei, a pair neutron transfer channel with positive Q-value is expected to influence the sub-barrier fusion dynamics. However, such a neutron transfer channel is not included in the present coupled channel calculations. As a result, the present coupled channel calculations are slightly deviated with respect to the fusion data, particularly in sub-barrier energy regions.$ {\chi ^2} $-analysis for SAGBD calculations and coupled channel calculations suggests that $ {\chi ^2} $-values for SAGBD outputs are reasonable. A detailed study of ⁴⁰Ca+^46,48,50Ti reactions, theoretical formalism, and results and conclusions ofthis work are presented in Sections II, III, and IV, respectively.

Based on partial wave analysis, total fusion cross-sections for spherical fusing nuclei can be written as

In the above equation, $ T_l^F $ represents the transmission coefficient for the ${l^{{\rm{th}}}}$ partial wave, and ${k^2} = \dfrac{{2\mu \,{E_{\rm c.m.}}}}{{{\hbar ^2}}}$. According to quantum mechanics, $ T_l^F $ can be obtained by solving the Schrödinger wave equation for the given interaction barrier. However, it may be fruitful to use an approximation for the transmission probability $ T_l^F $ in Eq. (1). Based on parabolic approximation of the interaction barrier, Hill and Wheeler [50] suggested an analytical expression for transmission coefficient as

The following approximations for barrier position, barrier curvature, and barrier height were used by Wong [37]:

Substituting Eq. (2) into Eq. (1) and using the abovementioned approximations from Eq. (3) to Eq. (5) for barrier characteristics, Wong simplified the Hill-Wheller approximation to generate a suitable formula for fusion cross-sections:

where $ {V_{CB}} $, $ \hbar {\omega _B} $, and $ {R_B} $ are the barrier height, barrier curvature, and barrier position, respectively. In the Wong formula, $ {V_{CB}} $, $ \hbar {\omega _B} $, and $ {R_B} $ are considered the same for all partial waves. One can consider the effects of deformation in the Wong formula by including deformed interaction potential, and this model is called the deformed Wong model. The effects of all dominant intrinsic degrees of freedom related to the nuclear structure of fusing partners appear through fluctuations of their radii. Therefore, to improve the predictions of the deformed Wong model, an additional radius parameter $\Delta R$ is used, and its value is optimized to compensate for the effects of dominant channel couplings along fusion pathway and hence reproduce the fusion data of a given reaction under consideration. $\Delta R$ depends on the nature of projectile-target combinations as well as on various static and dynamic physical effects occurring along the fusion path. For a given reaction, $\Delta R$ (depending upon projectile-target combinations) partially or fully accounts for the effects of static and dynamic deformation and/or neutron transfer channel through variation in the radii of collision parameters. To consider the effects of quadrupole deformation $({\beta _2})$ for projectile (or target), Woods-Saxon potential has been used, which is defined as

The first term of Eq. (7) is the Woods-Saxon form of nuclear potential, and second term is the Coulomb potential between spherical nuclei. The potential parameters ${V_0}$ and ${a_0}$ are depth and diffuseness, respectively, for Woods-Saxon potential. ${R_P}$ and ${R_T}$ are the radii of the projectile and target, respectively. ${Z_P}({Z_T})$ is the charge on the projectile (target) nucleus. $\Delta R$ is a radius parameter, which is taken as fixed for a given reaction. At $r = {R_B}$, the Coulomb barrier is the total interaction potential for partial wave $l = 0$. Hence,

where $ V(r) $ is the combination of nuclear and Coulomb potential, called total fusion barrier or Coulomb barrier for $l = 0$ partial wave at $r = {R_B}$:

The relation between the radius parameter ($ {R_0} $) and range parameter (or reduced radius parameter $ {r_0} $) is $ {R_0} = {r_{0\,}}\left( {A_P^{1/3} + A_T^{1/3}} \right) $, and$ {V_0} $ and $ {a_0} $ are the depth and diffuseness of the selected nuclear potential, respectively. At $r = {R_B}$, the height of Coulomb barrier is defined as

The barrier position for the Coulomb barrier is given by

and using the above condition, one obtains

The barrier curvature ($\hbar {\omega _B}$) of the Coulomb barrier is evaluated by taking the conditions given in Eqs. (13) and (14).

By employing the conditions given in Eqs. (7) to (14), parameters for the Coulomb barrier, such as barrier height, barrier position, and barrier curvature, are extracted and used for theoretical calculations of the fusing partners. The deformed nuclear potential [38−42] is given as

The effects of deformations in deformed nuclear potential are considered in terms of radii of fusing nuclei as follows:

where $\lambda = 2,4,6$, and $i$ refers to projectile (or target). In the above expression, ${Y_{\lambda 0}}(\theta )$ and ${\beta _{\lambda i}}$ are spherical harmonics and deformations, respectively. Using deformed nuclear potential in the Wong formula, the fusion cross-sections are calculated. ${R_{i0}}$ is the radius of spherical nucleus, which is given as

For axially deformed nuclei, the radii can be defined by

with ${R_P}(\beta ,\theta )$ and ${R_T}(\beta ,\theta )$ defined as

Here, $\theta $ is the angle between the symmetric axis of the projectile (or target) and collision axis. ${\beta _{2P}}$(${\beta _{2T}}$), ${\beta _{4P}}$(${\beta _{4T}}$), and ${\beta _{6P}}$(${\beta _{6T}}$) are quadrupole, hexadecapole, and hexacontatetrapole deformation of projectile (target), respectively. ${R_{P0}}$(${R_{T0}}$) is the radius of spherical projectile (target). If the projectile and target are spherical in shape (without deformation), then ground state deformations are ${\beta _{2P}} = {\beta _{2T}} = {\beta _{4P}} = {\beta _{4T}} = {\beta _{6P}} = {\beta _{6T}} = 0$, ${R_P}({\beta _P},{\theta _P}) = {R_{P0}} = {r_{P0}}A_P^{1/3}$, and ${R_T}({\beta _T},{\theta _T}) = {R_{T0}} = {r_{T0}}A_T^{1/3}$ with ${r_{P0}} = {r_{T0}} = {r_0}$. ${Y_{20}}(\theta )$, ${Y_{40}}(\theta )$, and ${Y_{60}}(\theta )$ are spherical harmonics for axially deformed nuclei with $\lambda = 2,4$, and $\lambda = 6$, respectively. To retrieve the fusion cross-section data, the effects of static deformation in the ground state of projectile and target are considered through nuclear potential.

Now, after rearranging Eq. (6), one obtains

First, differentiate Eq. (21) with respect to ${E_{\rm c.m.}}$, and after differentiation, we have

Because barrier distribution is defined as the second-order derivative of Eq. (21), i.e., ${\sigma ^{\rm Wong}}{E_{\rm c.m.}}$ relative to ${E_{\rm c.m.}}$, it is expressed as

In the above equation, $T$ is the probability for tunneling through the fusion barrier and hence is given as

On rearrangement of terms, one gets

After substitution of Eq. (27) into Eq. (26), ${D_f}({V_{CB}})$ (effective barrier distribution) is defined as

The behaviour of Eqs. (28) and (29) is like the Dirac delta function. Eqs. (26) and (29) show a single peak, and when ${E_{\rm c.m.}} = {V_{CB}}$, the nature of this single peak is symmetric. The expression for width of peak is defined using a relation of barrier curvature as $\hbar {\omega _B}\ln {{(3 + \sqrt 8 )} /\pi } = 0.56\hbar {\omega _B}$[43−48]. Stelson et al. [51] and others [52−54] suggested that the true form of real barrier distribution can be approximately reproduced by taking a Gaussian function type of weight function. Because${D_f}({V_{CB}})$ obeys the condition of normalization, ${D_f}({V_{CB}})$ is given as

Within the SAGBD model, total fusion cross-sections are obtained by incorporation of a Gaussian function as a weight function to simple Wong formula as

In Eq. (31), ${\sigma ^{\rm Wong}}\,({E_{\rm c.m.}},\,{V_{CB}})$ is the simple Wong formula, and ${D_f}\left( {{V_{CB}}} \right)$ is the effective barrier distribution. ${D_f}({V_{CB}})$ is a homogenous function, which is normalized as well as continuous and therefore computed as

The standard deviation ($ \Delta $) is expressed as half width at 60% of the full height of ${D_f}({V_{CB}})$. The theoretical mean barrier height of the main barrier distribution peak is given by ${V_{Bx}}$ as

The approximate value of ${V_{\rm eff}}$ lies within the range of

In the above expression, ${V_{\rm eff}}$ is effective fusion barrier and is evaluated by retrieving the structure of real experimental barrier distribution. The presence of intrinsic degrees of freedom is elucidated by model parameters ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$. Mathematically, ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$ are

${\lambda ^{\rm SAGBD}}$ is channel coupling parameter, and its value is directly related to the contributions of intrinsic channels related to the nuclear structure of projectile (or target) during the fusion process. ${V_{\rm CBRED}}$ describes the percentage decrease of the effective fusion barrier between participants relative to uncoupled Coulomb barrier due to the involvement of the dominant channel coupling effect during the fusion process.

The coupled channel approach is used to identify the influences of distinct internal structure degrees of freedom of fusing pairs on fusion process and for investigations of fusion data for discrete projectile-target systems. In the coupled channel approach, coupled differential equations are numerically solved by using incoming wave boundary conditions (IWBCs) and by using no-Coriolis approximation. In the no-Coriolis approximation, one can replace angular momentum of relative motion of each channel by total angular momentum. The no-Coriolis approximation is used to reduce the dimensions of the coupled differential equations. In incoming wave boundary conditions (IWBCs), incoming waves and outgoing waves of unit amplitude are at $r = {r_{\min }}$ and infinity, respectively, for all channels except for the $n = 0$ entrance channel.

In the above equation, $ {\varepsilon _n} $, $ \mu $, and $\vec r$ denote the n^th channel excitation energy, reduced mass of fusing nuclei, and radial co-ordinate between fusing partners, respectively. $ V_N^{(0)} $ is Woods-Saxon potential, while ${V_{nm}}$ corresponds to the coupling matrix element of the coupling Hamiltonian. The conventional Woods-Saxon potential is used to integrate the effects due to various channels in computations and hence acts as an input for computations. Under the impacts of the above approximations for solution, total fusion cross-sections for fusing reactions are stated as

$ {k_0} $ is the wave vector for the entrance channel. For total angular momentum $(J)$, ${P_J}({E_{\rm c.m.}})$ is tunneling probability. For selected reactions, fusing participants are well known for their distinct vibrational state; hence, by considering these states, the current calculations are carried out with harmonic limit for 2⁺ and 3^– vibrational states of colliding nuclei. The values of several parameters used for coupled channel calculations are listed in Tables 4 and 5.

For the studied systems, potential depth is kept fixed at $150\;{\rm{MeV}}$, and other parameters such as diffuseness $({a_0})$ and range $({r_0})$ are varied to get a consistent fit with the experimental data above barrier energies using the simple Wong formula. These potential parameters, as listed in Table 1, are used to obtain the barrier characteristics of the Coulomb barrier, as listed in Table 2. By using the conditions given in Eqs. (8) to (14), the obtained barrier characteristics are indexed in Table 2. In the SAGBD model, the Coulomb barriers for ⁴⁰Ca + ⁴⁶Ti, ⁴⁰Ca + ⁴⁸Ti, and ⁴⁰Ca + ⁵⁰Ti reactions with an optimal diffuseness are 61.290 MeV, 61.160 MeV, and 60.320 MeV, respectively. The same parameters are used in SAGBD calculations with an optimal diffuseness. To investigate the sensitivity of fusion data towards the choice of potential parameters, different diffuseness parameterizations like Winther and Akyüz-Winther diffuseness and an optimal diffuseness are utilized within the SAGBD model to predict the behaviour of fusion dynamics of ⁴⁰Ca + ^46,48,50Ti reactions. Winther and Akyüz-Winther diffuseness within the SAGBD model do not reproduce the sub-barrier fusion data of given reactions; therefore, the value of diffuseness is optimized with respect to the value of Winther and Akyüz-Winther diffuseness. An optimal diffuseness parameter, which is larger than Winther and Akyüz-Winther diffuseness within the SAGBD model, is able to retrieve experimental data in all domains of incident beam energies. The results due to various diffuseness schemes on fusion barrier, fusion cross-sections, and barrier distributions for ⁴⁰Ca + ^46,48,50Ti systems are shown in Figs. 1−4, respectively. Winther [24] and Aky$ \ddot{\mathrm{u}} $z-Winther [25] diffuseness parameterizations are given as

Fusion reactions	Potential depth ${V_0}$ /MeV	Winther diffuseness	Aky$ \ddot{\mathrm{u}} $z-Winther diffuseness	Optimum diffuseness ${a_0}$ /fm	Range ${r_0}$/fm
40Ca + 46Ti	150	0.656	0.676	0.760	1.00
40Ca + 48Ti	150	0.657	0.677	0.750	1.01
40Ca + 50Ti	150	0.658	0.678	0.750	1.01

Table 1.  Potential parameters chosen for SAGBD calculations for ⁴⁰Ca + ^46,48,50Ti systems.

Fusion reactions	Coulomb barrier ${V_{CB}}$ /MeV	Barrier position ${R_B}$/fm	Barrier curvature $\hbar {\omega _B}$ /MeV
40Ca + 46Ti	61.290	9.480	3.925
40Ca + 48Ti	61.160	9.510	4.151
40Ca + 50Ti	60.320	9.660	3.602

Table 2.  Barrier characteristics of Coulomb barrier used in the SAGBD calculations for chosen reactions.

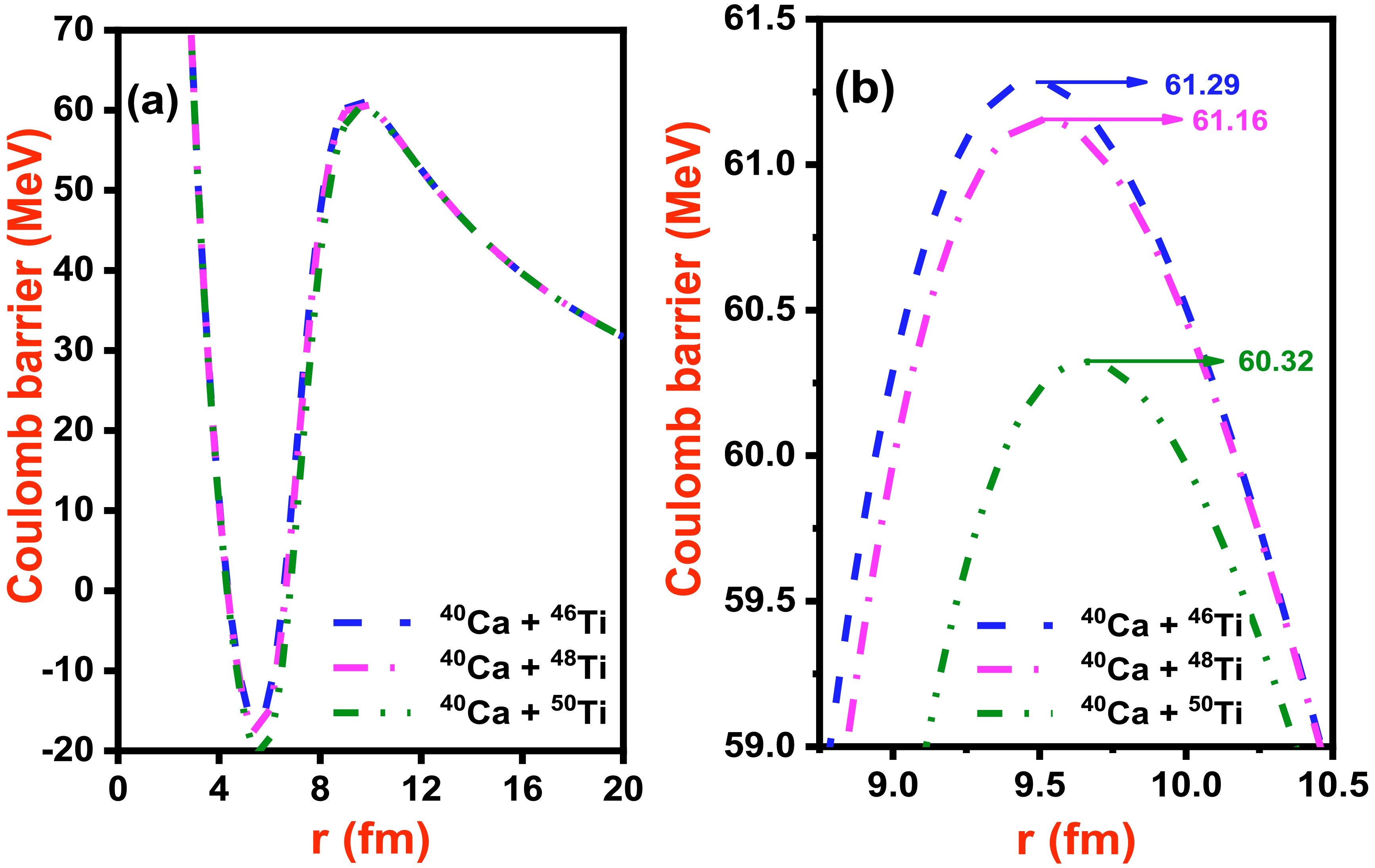
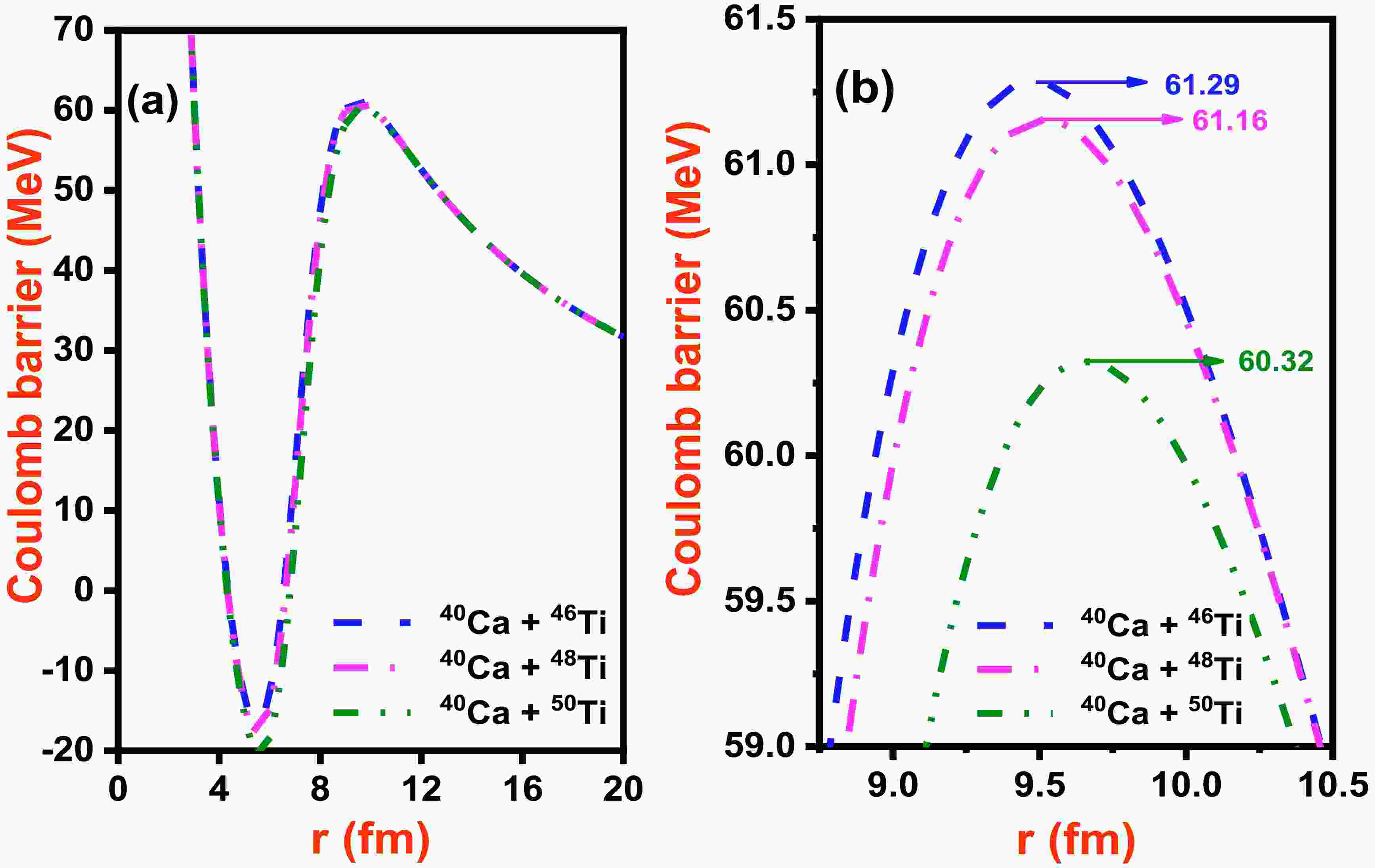
Figure 1.  (color online) For $l = 0$ partial waves, radial dependence of the Coulomb barrier for (a) ⁴⁰Ca + ^46,48,50Ti systems, and (b) same as (a) but at near-barrier position ${R_B}$.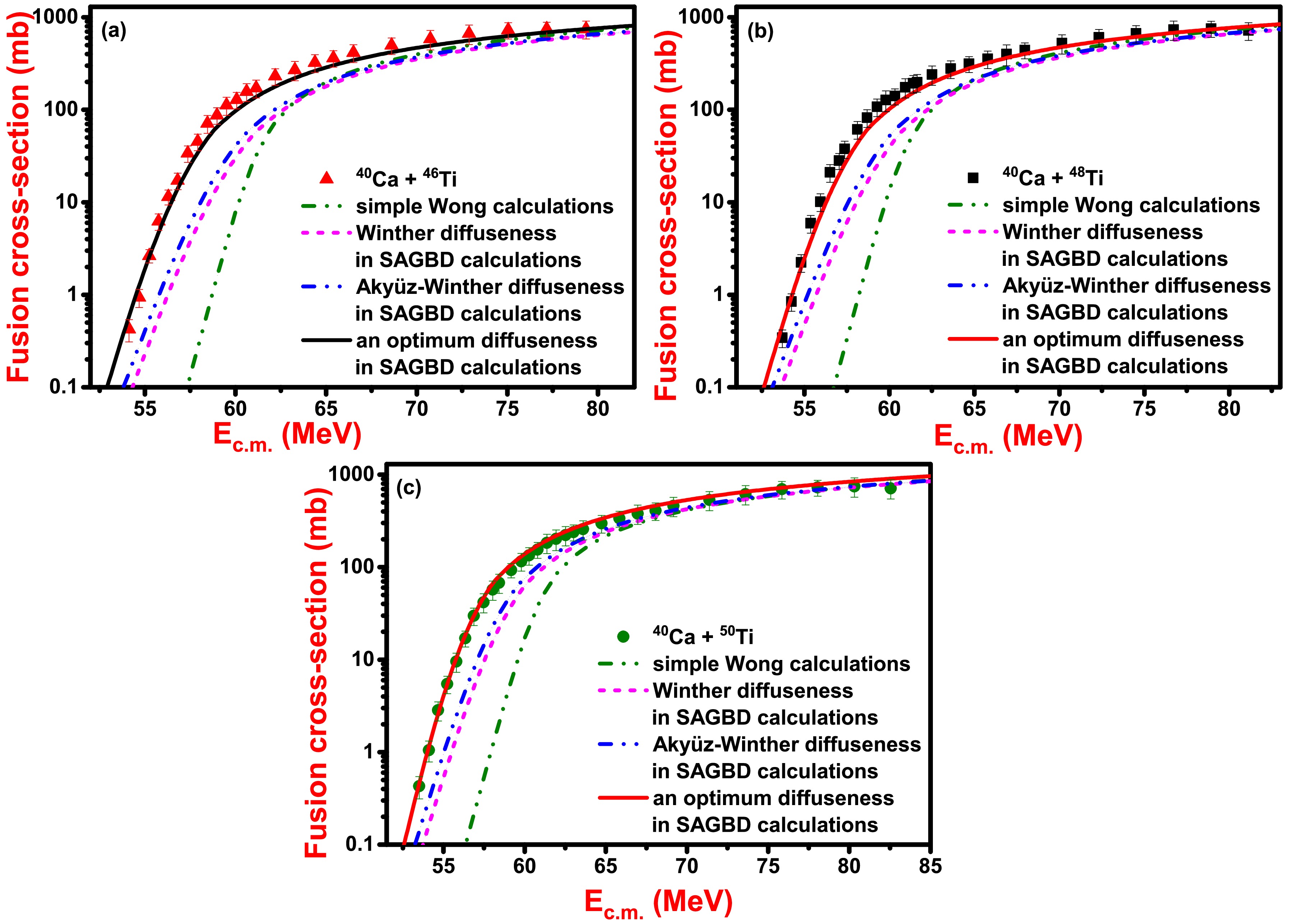

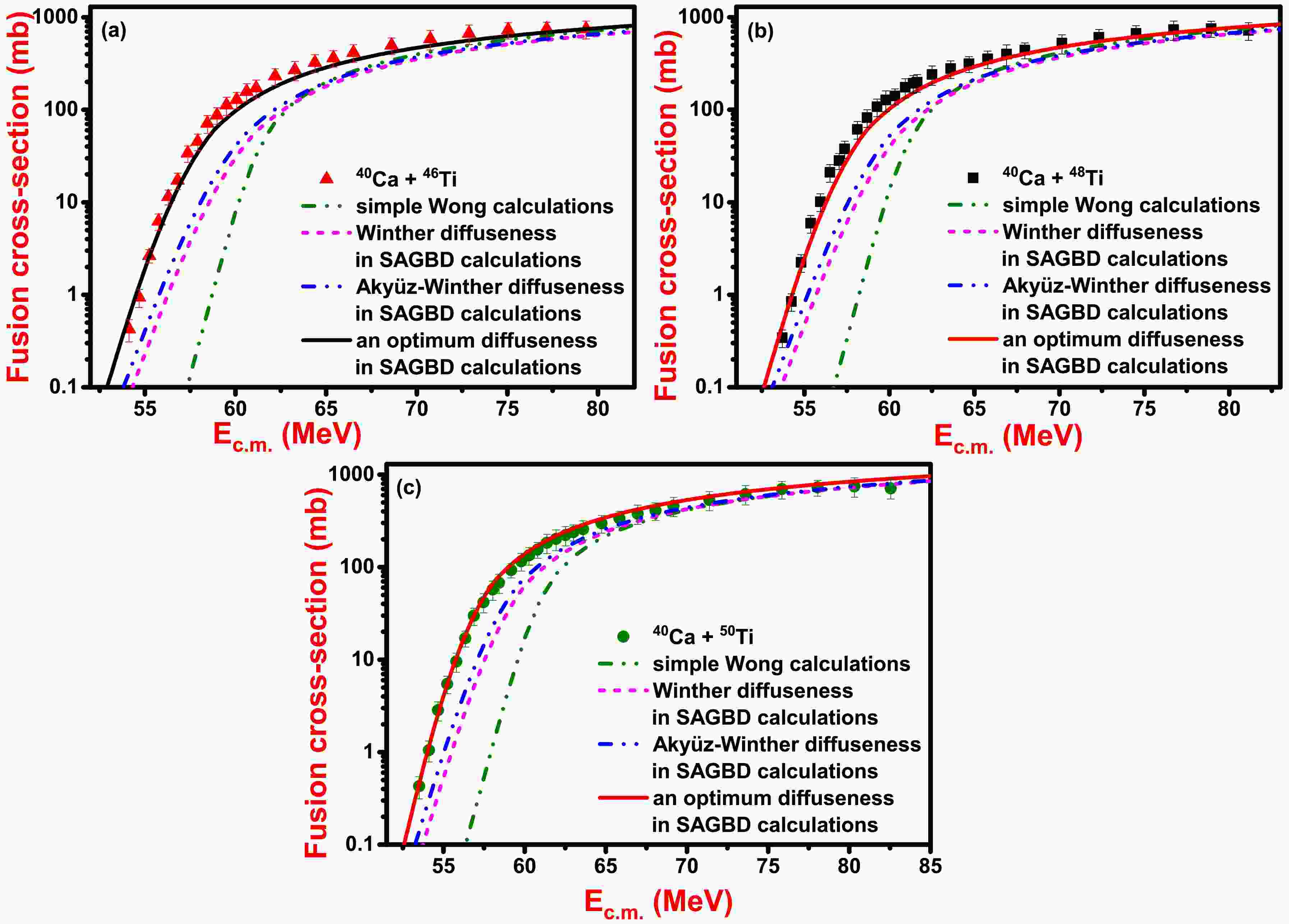
Figure 2.  (color online) Fusion cross-sections as a function of ${E_{c.m.}}$ for (a) ⁴⁰Ca + ⁴⁶Ti, (b) ⁴⁰Ca + ⁴⁸Ti, and (c) ⁴⁰Ca + ⁵⁰Ti reactions obtained using Wong formula and SAGBD model with Winther diffuseness, Aky$ \ddot{\mathrm{u}} $z-Winther diffuseness, and optimal diffuseness. The experimental data of these systems are taken from Ref. [36] and also compared with theoretical predictions.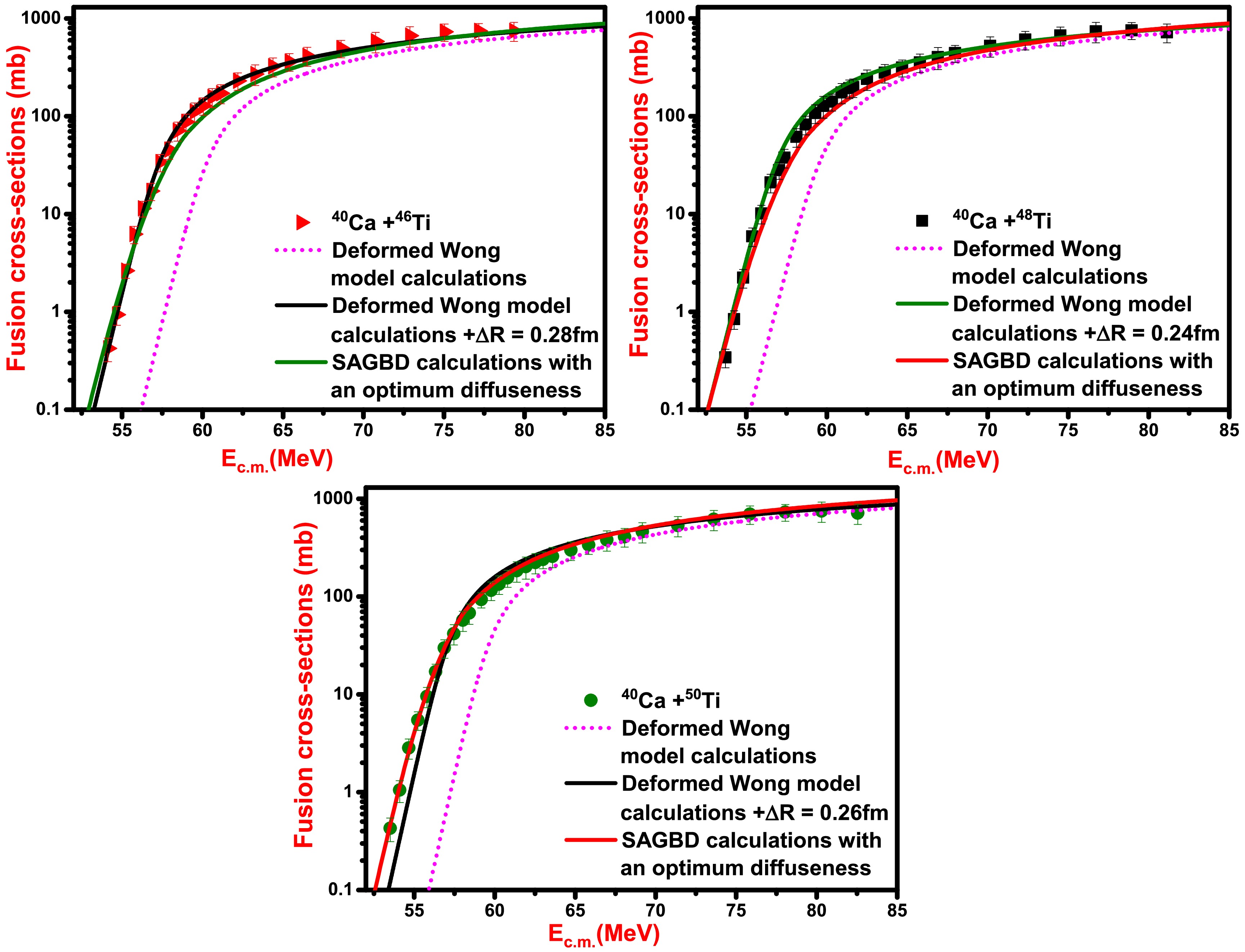

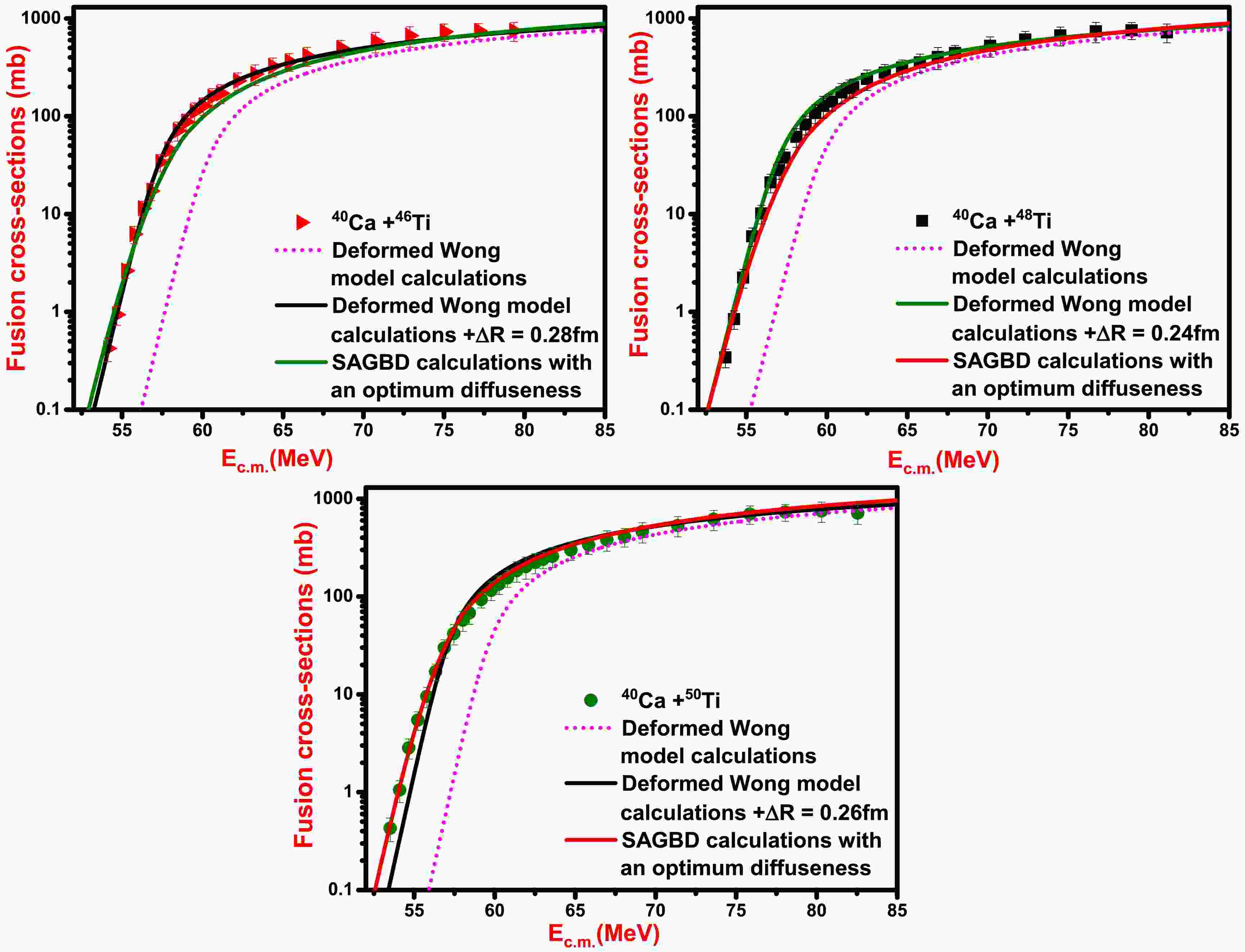
Figure 3.  (color online) Fusion cross-sections for the reactions of ⁴⁰Ca+ ^46,48,50Ti as a function of ${E_{\rm c.m.}}$ obtained using deformed Wong model, deformed Wong model with $\Delta R$, and SAGBD model.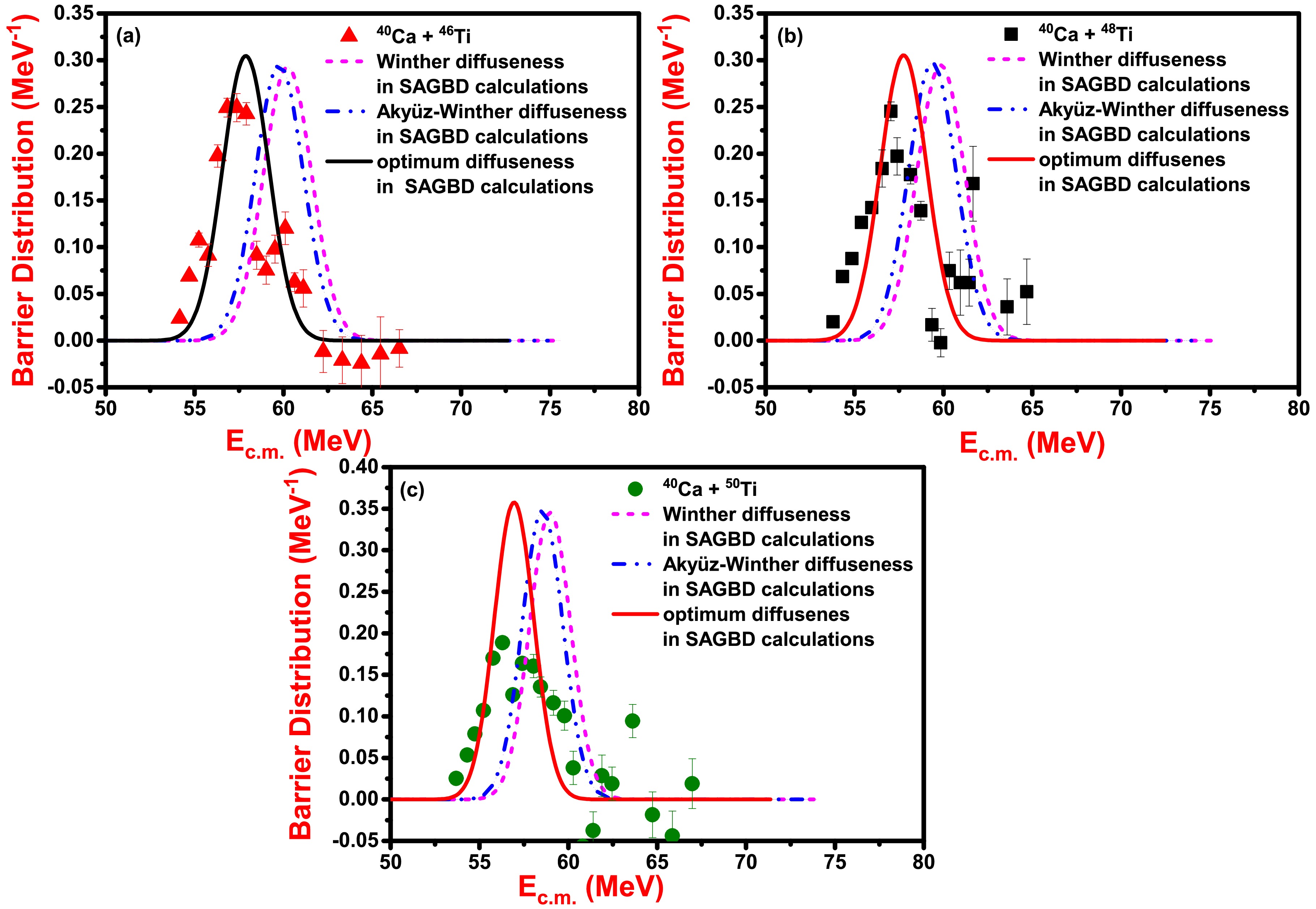

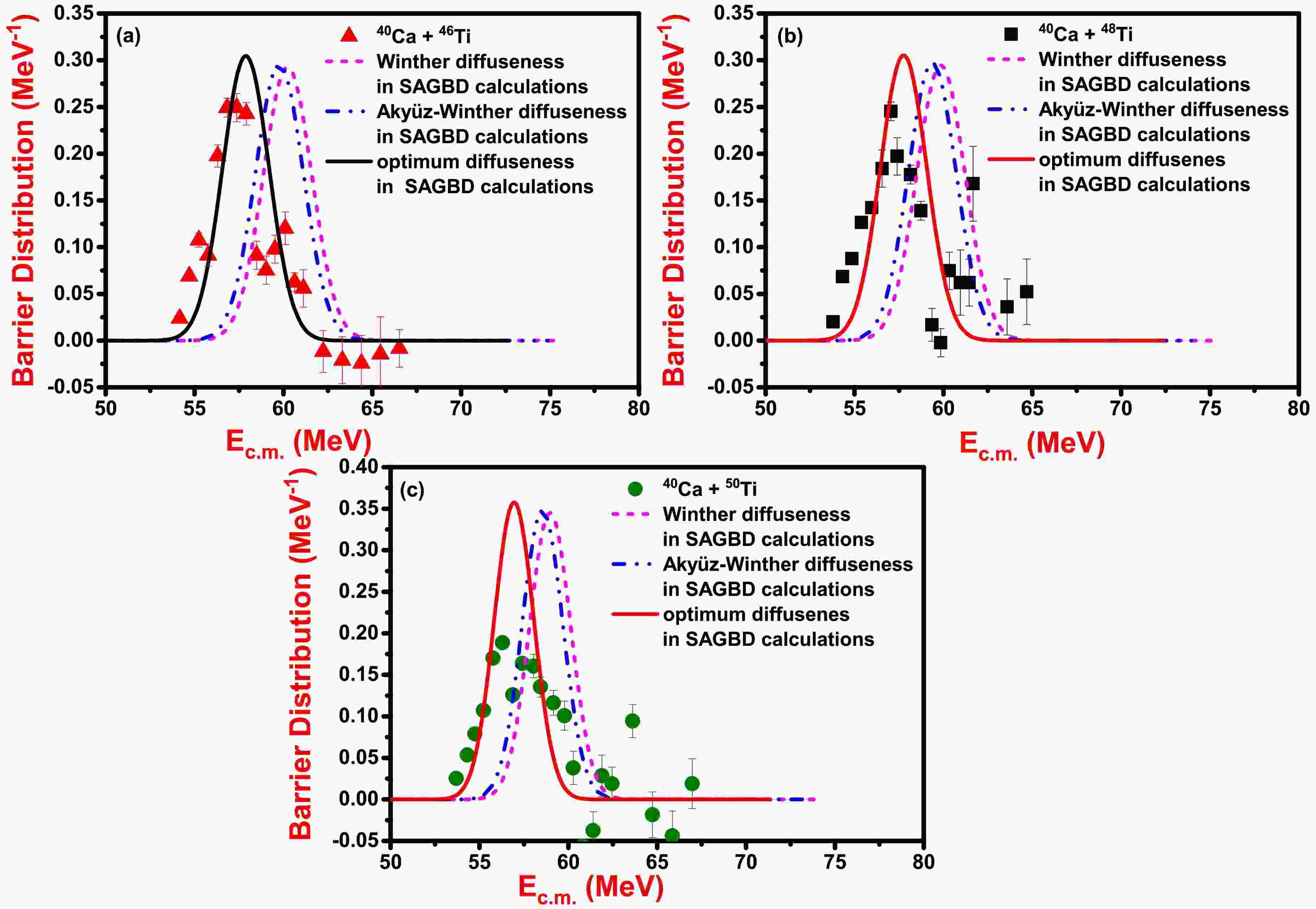
Figure 4.  (color online) Fusion barrier distribution as a function of ${E_{\rm c.m.}}$ for (a) ⁴⁰Ca + ⁴⁶Ti, (b) ⁴⁰Ca + ⁴⁸Ti, and (c) ⁴⁰Ca + ⁵⁰Ti reactions obtained using SAGBD model with Winther diffuseness, Aky$ \ddot{\mathrm{u}} $z-Winther diffuseness, and optimal diffuseness parameter. The theoretical calculations due to the SAGBD model are compared with the experimental data taken from Ref. [36].

1. Winther diffuseness:

2. Aky$ \ddot{\mathrm{u}} $z-Winther diffuseness:

Before going into detail with the theoretical calculations, let us first analyze the dependence of interaction barrier as a function of separation coordinate between fusing nuclei. The Coulomb barrier between projectile and target for various systems ⁴⁰Ca + ^46,48,50Ti as a function of radial separation are displayed in Fig. 1(a). 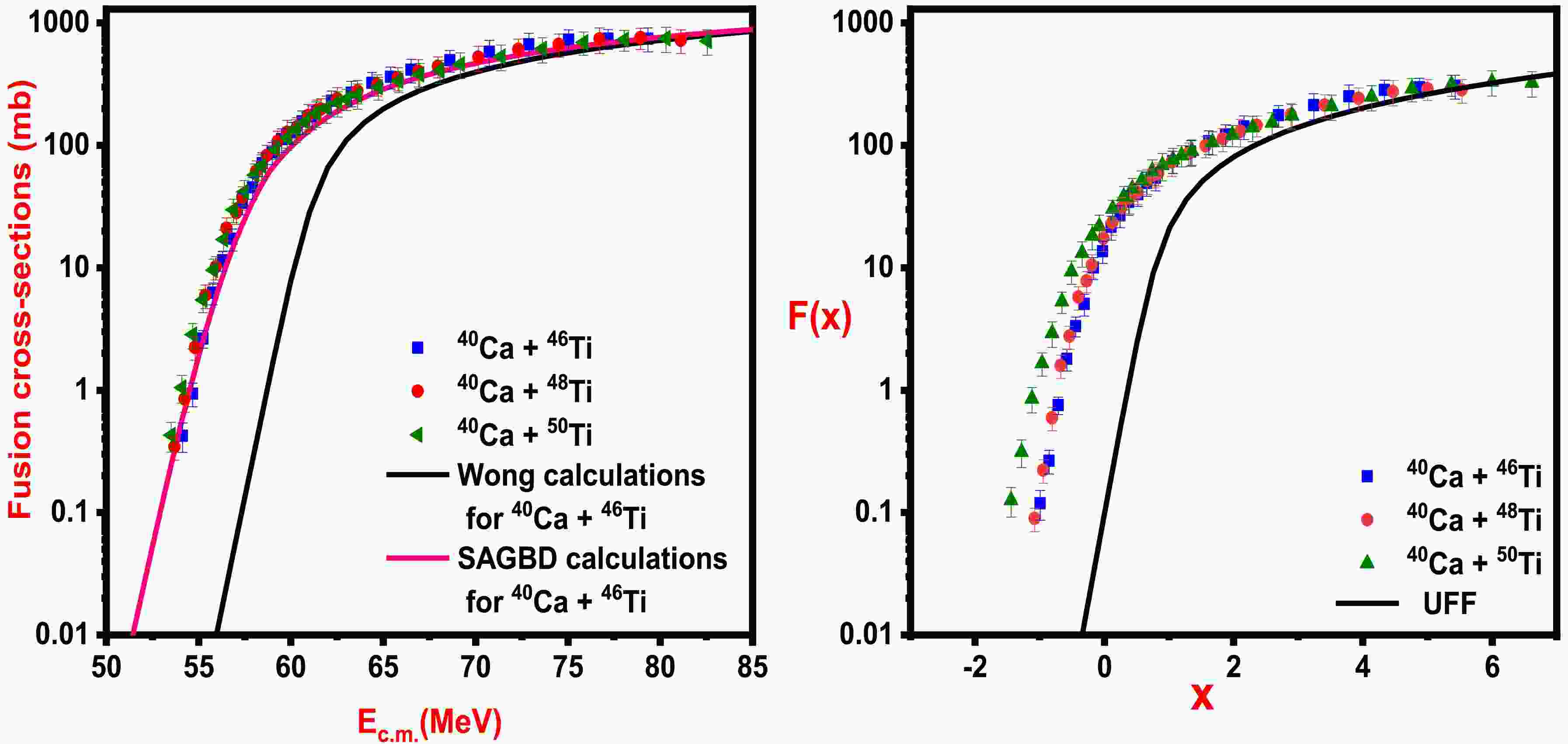Figure 1(b) represents the zoom of Coulomb barrier for the chosen systems near the peak value or around the barrier position ${R_B}$, and for chosen systems, one can easily notice that the results of theoretical predictions in the sub-barrier domain are different due to different radial dependence of their fusion barriers. As the barrier characteristics of selected reactions turned out to be different, the nature of fusion cross-sections in the sub-barrier realm come out differently. From Fig. 1, one can comprehend that for ⁴⁰Ca + ^46,48,50Ti systems, the increase in neutron richness of target isotope brings a decrease in the Coulomb barrier. In the literature [36], it was highlighted that the lowest fusion barrier is offered by larger-mass asymmetric systems that appeared for the heaviest Ti-isotopes, as expected. For the heaviest target isotopes, the entrance channel mass asymmetry as well as probability of neutron transfer channel with positive Q-value is largest, and hence, these two factors favour larger sub-barrier fusion enhancement for a heavier target isotope (⁵⁰Ti) in comparison to lighter target isotopes (^46,48Ti).

In Fig. 2, fusion cross-sections estimated using the simple Wong formula and SAGBD model with different parameterizations of diffuseness are shown. For all the studied systems, theoretically estimated fusion cross-sections using the simple Wong formula remain much smaller than the experimental data at sub-barrier energies. However, above the energies, calculations based on the simple Wong formula are reasonable with fusion data, further suggesting that relative motion between colliding pairs is enough for the description of fusion data. To describe sub-barrier fusion data, dominant intrinsic channels of fusing pairs must be included in theoretical description. For this aspect, the SAGBD model is employed to interpret the fusion data of ⁴⁰Ca + ^46,48,50Ti reactions. The SAGBD model does not include the coupling of intrinsic channels with the relative motion between the fusing partners directly but makes use of a Gaussian function as the weight function in the simple Wong formula. Further, to assess the sensitivity of potential parameters associated with Woods-Saxon potential for ⁴⁰Ca + ^46,48,50Ti reactions, effects on variation of diffuseness parameter of Woods-Saxon potential are investigated within the preview of the SAGBD model. SAGBD calculations with Winther and Akyüz-Winther parameterizations of diffuseness are conducted for given systems; however, such calculations do not explain fusion data of given reactions in near- and sub-barrier regions. Therefore, the diffuseness parameter is optimized in comparison to Winther and Akyüz-Winther parametrization and by using an optimized diffuseness parameter (${a_0} = 0.760\;{\rm{fm}}$ for ⁴⁰Ca + ⁴⁶Ti and ${a_0} = 0.750\;{\rm{fm}}$ for ⁴⁰Ca + ^48,50Ti). Within SAGBD calculations, the estimated fusion cross-sections of ⁴⁰Ca + ^46,48,50Ti reactions reproduce experimental data in the full range of incident beam energies. One will see later that the outcomes of SAGBD calculations with an optimum diffuseness seem to be identical to those of coupled channel predictions. The impacts of channel coupling on the fusion process are expressed in terms of channel coupling parameter ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$. The effective potential used for estimation of coupling parameter ${\lambda ^{\rm SAGBD}} $ and ${V_{\rm CBRED}} $ as well as position of effective radius corresponding to effective potential are indexed in Table 3. The values of ${\lambda ^{\rm SAGBD}}$ for the ⁴⁰Ca + ⁴⁶Ti, ⁴⁰Ca + ⁴⁸Ti, and ⁴⁰Ca + ⁵⁰Ti systems are 3.38, 3.44, and 3.46, respectively. ${V_{\rm CBRED}}$ for the ⁴⁰Ca + ⁴⁶Ti, ⁴⁰Ca + ⁴⁸Ti, and ⁴⁰Ca + ⁵⁰Ti systems are 5.51% of ${V_{CB}}$, 5.62% of ${V_{CB}}$, and 5.73% of ${V_{CB}}$, respectively. The non-zero values of channel coupling parameter (${\lambda ^{\rm SAGBD}}$) imply that involvements of dominant intrinsic channels are significant in the fusion process. The positive value of ${V_{\rm CBRED}}$ for ⁴⁰Ca + ^46,48,50Ti reactions reflects that a reduction in fusion barrier between participants occurred due to participation of vibrational states of fusing nuclei and/or neutron transfer channels. The value of ${V_{\rm CBRED}}$ is larger for ⁴⁰Ca + ⁵⁰Ti than for ⁴⁰Ca + ^46,48Ti, which clearly reflects the contributions of neutron transfer channels with positive Q-value for ⁴⁰Ca + ⁵⁰Ti reactions, and such channels are absent in ⁴⁰Ca + ^46,48Ti reactions due to negative Q-value for neutron transfer channels.

System	${V_{\rm eff} }\,{\rm{/MeV} }$	${\lambda ^{\rm SAGBD} }$	${V_{\rm CBRED} }$	${R_{\rm eff} }\,{\rm{/fm} }$
40Ca + 46Ti	57.91	3.38	5.51	11.06
40Ca + 48Ti	57.72	3.44	5.62	11.11
40Ca + 50Ti	56.88	3.46	5.73	11.14

Table 3.  Parameters $({V_{\rm eff}})$, ${\lambda ^{\rm SAGBD}}$, $\rm FWHM$, $\Delta $, and ${V_{\rm CBRED}}$ estimated from SAGBD predictions for studied systems.

For the given systems, when a deformed choice of nuclear potential is taken within the simple Wong formula, it is called the deformed Wong model, and the deformation in nuclear shape of projectile and target are taken via radii of colliding nuclei. It is evident from Fig. 3 that for selected systems, the inclusion of quadrupole deformations (${\beta _2}$) for both projectile as well as target results in enhanced cross-sections, but such computations are still unable to retrace the fusion data. To incorporate the influences of nuclear structure properties of projectile and target and other static and dynamic physical effects into the fusion process, an additional radius parameter $\Delta R$ is optimized. The values of quadrupole deformations taken for calculations are given in Table 5, and the values of additional radius parameter $\Delta R$ for ⁴⁰Ca + ⁴⁶Ti, ⁴⁰Ca + ⁴⁸Ti, and ⁴⁰Ca + ⁵⁰Ti reaction are$\Delta R = 0.28\;{\rm{fm}}$, $\Delta R = 0.24\;{\rm{fm}}$, and $\Delta R = $ 0.26 fm, respectively. From Fig. 3, it is seen that involvement of quadrupole deformation (${\beta _2}$) of both fusing nuclei with an additional radius parameter $(\Delta R)$ is sufficient to include all the dominant channel couplings involved in the fusion process and hence reproduce the fusion data in the given energy range. The theoretical predictions due to the deformed Wong model are also found analogous to predictions of the SAGBD model (with an optimum diffuseness parameter) in sub-barrier energy regions, as evident in Fig. 3.

Nucleus	$ \,{\beta _2} $	${E_2}$/MeV	$\, {\beta _3} $	${E_3}$/MeV
40Ca	0.120	3.904	0.433	3.737
46Ti	0.317	0.899	0.122	3.059
48Ti	0.269	0.983	0.147	3.358
50Ti	0.166	1.555	0.156	4.410

Table 5.  Quadrupole deformation $({\beta _2})$ and octupole deformation $({\beta _3})$ and their excitation energies ${E_2}$ and ${E_3}$, respectively, for different nuclei.

Figure 4 shows the barrier distributions for ⁴⁰Ca + ^46,48,50Ti reactions that are obtained by incorporating different parametrizations of diffuseness into SAGBD model. With Winther and Akyüz-Winther diffuseness in the SAGBD model, theoretical calculations are unable to retrieve the shape of experimental barrier distribution; the main peak of the theoretical barrier distribution appeared on the right side of the uncoupled Coulomb barrier, as evident from Fig. 4. This reflects that the height of the Coulomb barrier with Winther & Akyüz-Winther diffuseness is larger than that with optimal diffuseness. The displacement of the main peak of the theoretical barrier distributions towards the right of the uncoupled Coulomb barrier clearly demonstrates that theoretical predictions at sub-barrier energies consistently underestimate the experimental findings, as also evident from Fig. 2. Meanwhile, results of the barrier distributions with an optimal diffuseness reasonably recuperate the fusion data across the given range of incident beam energy. Hence, utilizing an optimal diffuseness is sufficient to regulate the dominant intrinsic channels in reaction dynamics.

Coupled channel calculations for ⁴⁰Ca + ^46,48,50Ti reactions are performed using CCFULL code, and the results are displayed in Fig. 5. The potential parameters, deformation parameter, and excitation energies of low-lying vibrational states for projectile and target are tabulated in Tables 4 and 5. As far as projectile (⁴⁰Ca) is concerned, the quadrupole deformation is small, and the first excited state lies at higher excitation energy. However, the first excited octupole vibrational state of the projectile lies lower than that of its corresponding quadrupole state. Further, octupole deformation is significantly larger than its quadrupole deformation and, in this sense, the projectile exhibits strong octupole vibrations. The contributions of low-lying vibrational states of projectile are found to be equal in all three reactions, as the projectile is common among three Ti-isotopes. As far as ^46,48,50Ti-isotopes are concerned, these nuclei have well-known vibrational spectra due to their spherical shape in the ground state. The quadrupole state of the ⁴⁶Ti-isotope has the highest strength, and its first excited state lies at the lowest energy among three Ti-isotopes. Therefore, the effects of quadrupole deformation in the ⁴⁶Ti-isotope are expected to be relatively large compared to its octupole vibrations and also expected to display significantly larger impacts on the fusion process compared to ^48,50Ti-isotopes. In a similar sense, the strength of quadrupole deformation in the ⁴⁸Ti-isotope is comparatively smaller than that in the ⁴⁶Ti-isotope but larger than that in the ⁵⁰Ti-isotope. Therefore, the effects of 2⁺ vibrational states of ⁴⁸Ti-isotope on the fusion process are smaller than those of ⁴⁶Ti but are expected to be larger than the effects of 2⁺ state on the ⁵⁰Ti-isotope. In the fusion process, inelastic surface vibrations are dominant; therefore, the magnitude of sub-barrier fusion enhancement of ⁴⁰Ca + ⁴⁶Ti is expected to be greater than that of ⁴⁰Ca + ^48,50Ti reactions. Following a similar analogy, the magnitude of sub-barrier fusion enhancement for the ⁴⁰Ca + ⁴⁸Ti reaction is also expected to be enhanced compared to that of the ⁴⁰Ca + ⁵⁰Ti reaction. Hence, strong collectivity of inelastic surface excitations for ^46,48,50Ti-isotopes is expected to appear for the considered reactions.

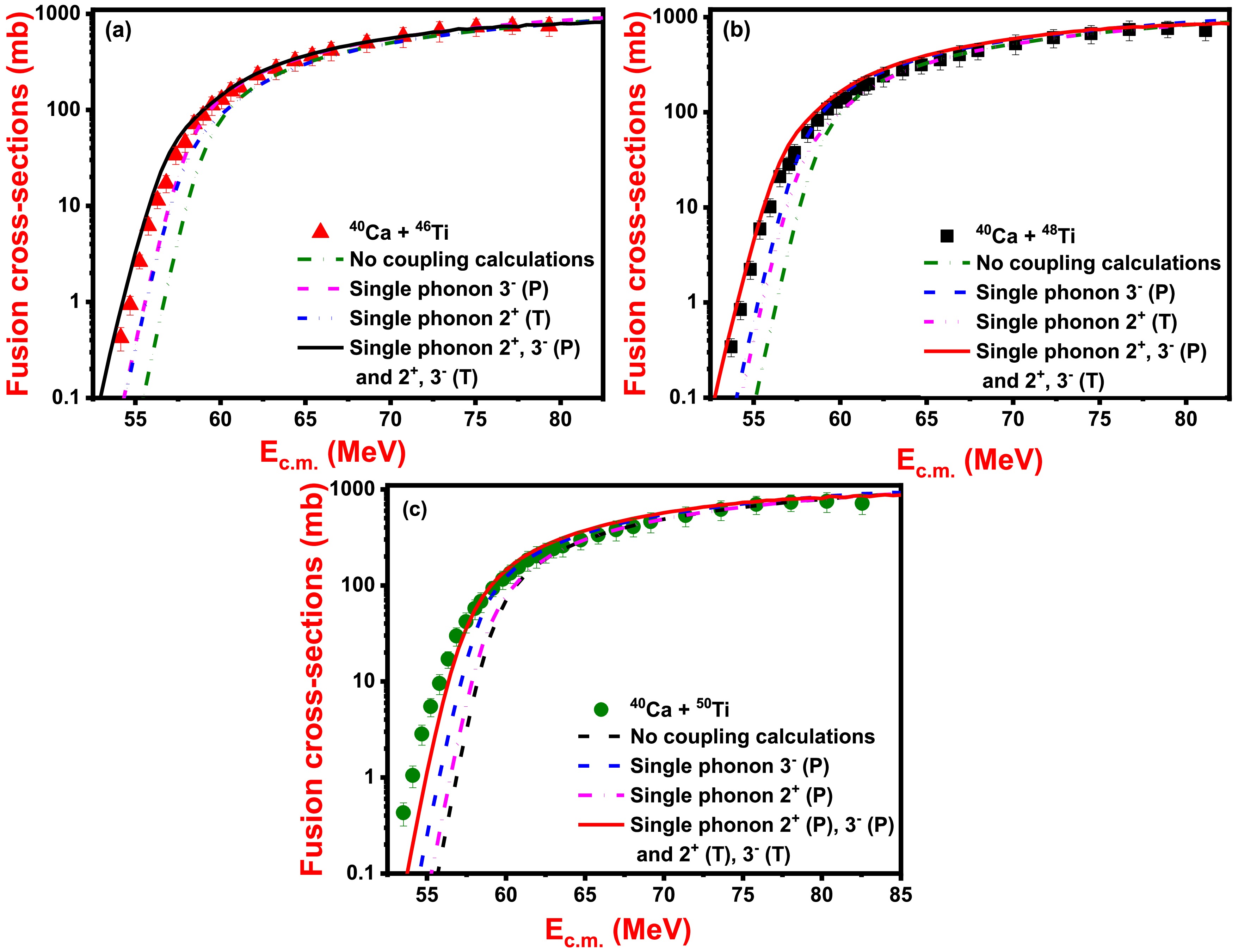
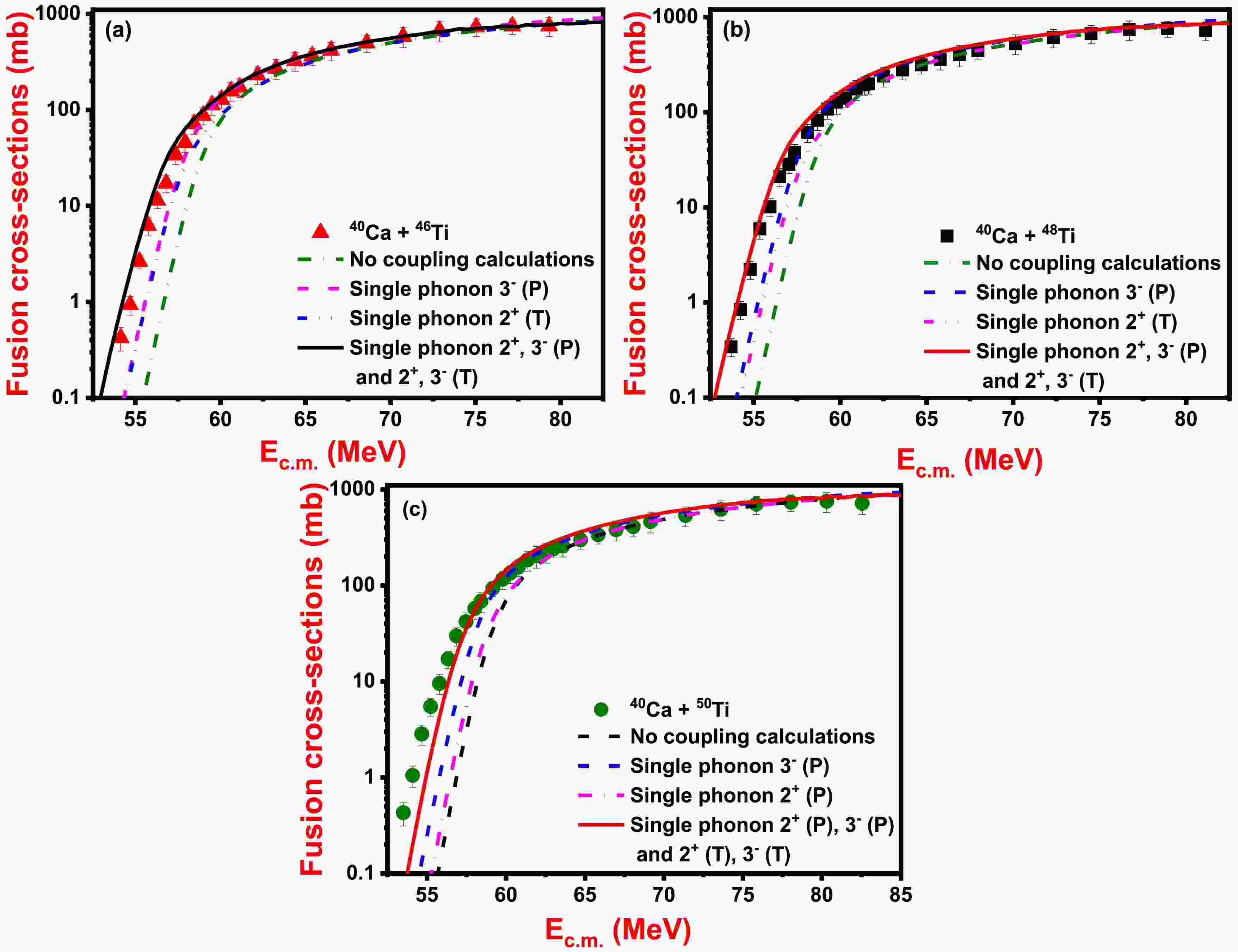
Figure 5.  (color online) Fusion cross-sections as a function of ${E_{\rm c.m.}}$ for (a) ⁴⁰Ca + ⁴⁶Ti, (b) ⁴⁰Ca + ⁴⁸Ti, and (c) ⁴⁰Ca + ⁵⁰Ti systems obtained from coupled channel calculations. The theoretical results are compared with experimental data taken from Ref. [36].

For ⁴⁰Ca + ⁴⁶Ti system, with no coupling scheme, the fusion cross-sections are found to be underpredicted with respect to sub-barrier fusion data. To retrace the sub-barrier fusion data, the contributions of single-phonon 3^– state in ⁴⁰Ca are considered, and outcomes are found to be enhanced with no coupling calculations, but such calculations are unable to obtain the desired results. The involvement of single-phonon quadrupole 2⁺ state of ⁴⁶Ti shows additional enhancement just like to the single-phonon 3^– state in ⁴⁰Ca, but such coupling is not sufficient to obtain the desired outcomes. The experimental data are retraced by invoking coupling of single-phonon 2⁺ and 3^– states of ⁴⁰Ca and 2⁺ and 3^– states of ⁴⁶Ti along with their mutual coupling, such as $ ({2^ + } \otimes {3^ - }) $for both fusing pairs (see Fig. 5(a)).

A similar coupling is employed for exploration of fusion dynamics for the ⁴⁰Ca + ⁴⁸Ti system. In the no coupling scheme, fusing nuclei are taken as inert, and estimated fusion cross-sections do not retrieve the fusion data in below-barrier regions. The fusion cross-sections obtained due to single-phonon 3^– state in ⁴⁰Ca results in enhanced cross-sections compared to no coupling but do not reproduce experimental data satisfactorily. The computations due to single-phonon 2⁺ state of ⁴⁸Ti result in an increased cross-sections with respect to its single-phonon octupole 3^– state but do not explain the experimental findings. The considerations of single-phonon 2⁺ and 3^– vibrational states of both ⁴⁰Ca and ⁴⁸Ti along with their mutual couplings, such as $ ({2^ + } \otimes {3^ - }) $ state, give a reasonable reproduction of fusion data of the given reaction in the defined energy range, as shown in Fig. 5(b).

In the no coupling case, for the ⁴⁰Ca + ⁵⁰Ti reaction, the estimated cross-sections do not recover experimental data at below-barrier energies and thus suggests the incorporation of more intrinsic channels. Thus, to describe the fusion data points, the same coupling scheme as used for ⁴⁰Ca + ^46,48Ti reactions was used in the coupled channel description. The incorporation of single-phonon 2⁺ and 3^– states in ⁴⁰Ca results in enhanced cross-sections regarding uncoupled calculations but still could not reproduce the desired results. Consideration of the single-phonon 2⁺ state of ⁵⁰Ti produces large cross-sections relative to coupling to the single-phonon 3^– state of ⁴⁰Ca, but this calculation does not retrieve the anticipated experimental data. However, the coupling to single-phonon 2⁺ and 3^– states of ⁴⁰Ca and ⁵⁰Ti along their mutual coupling fairly account for experimental data. The small discrepancies between sub-barrier experimental data and theoretical coupled channel calculations based on couplings to inelastic surface excitations of the collision partners reflects that some additional channels are required to explain the sub-barrier fusion data of the given system. As this reaction offers the possibility of a pair transfer channel with positive Q-value, henceforth, coupling to the 2n-transfer channel is requisite to describe the experimental data completely. However, in the present coupled channel calculations, such a transfer channel is not included to single out the effects of inelastic surface vibration couplings from those of neutron transfer couplings. Also, the coupled channel predictions reasonably address the fusion data without considering a pair neutron transfer channel for the given reaction.

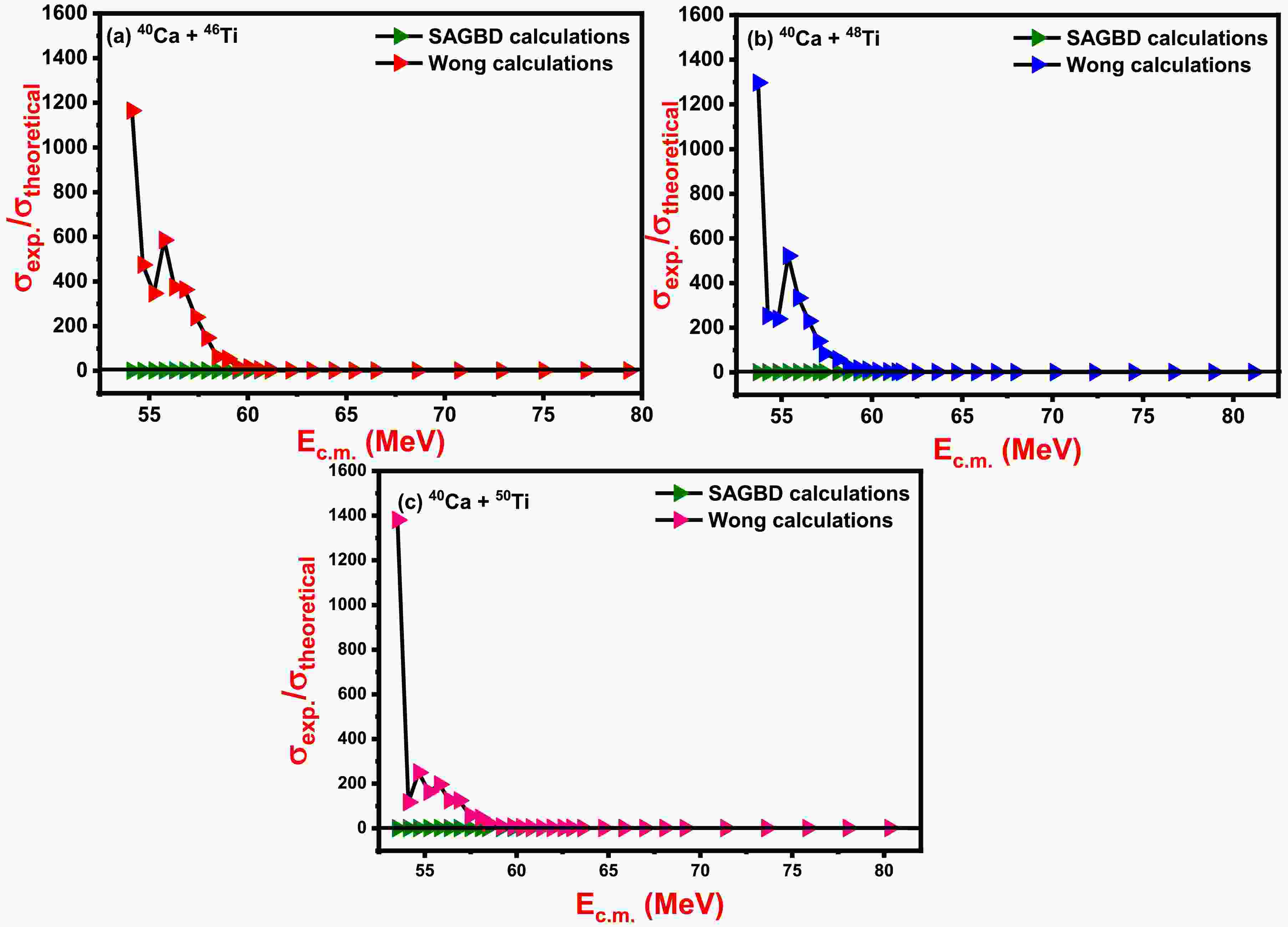
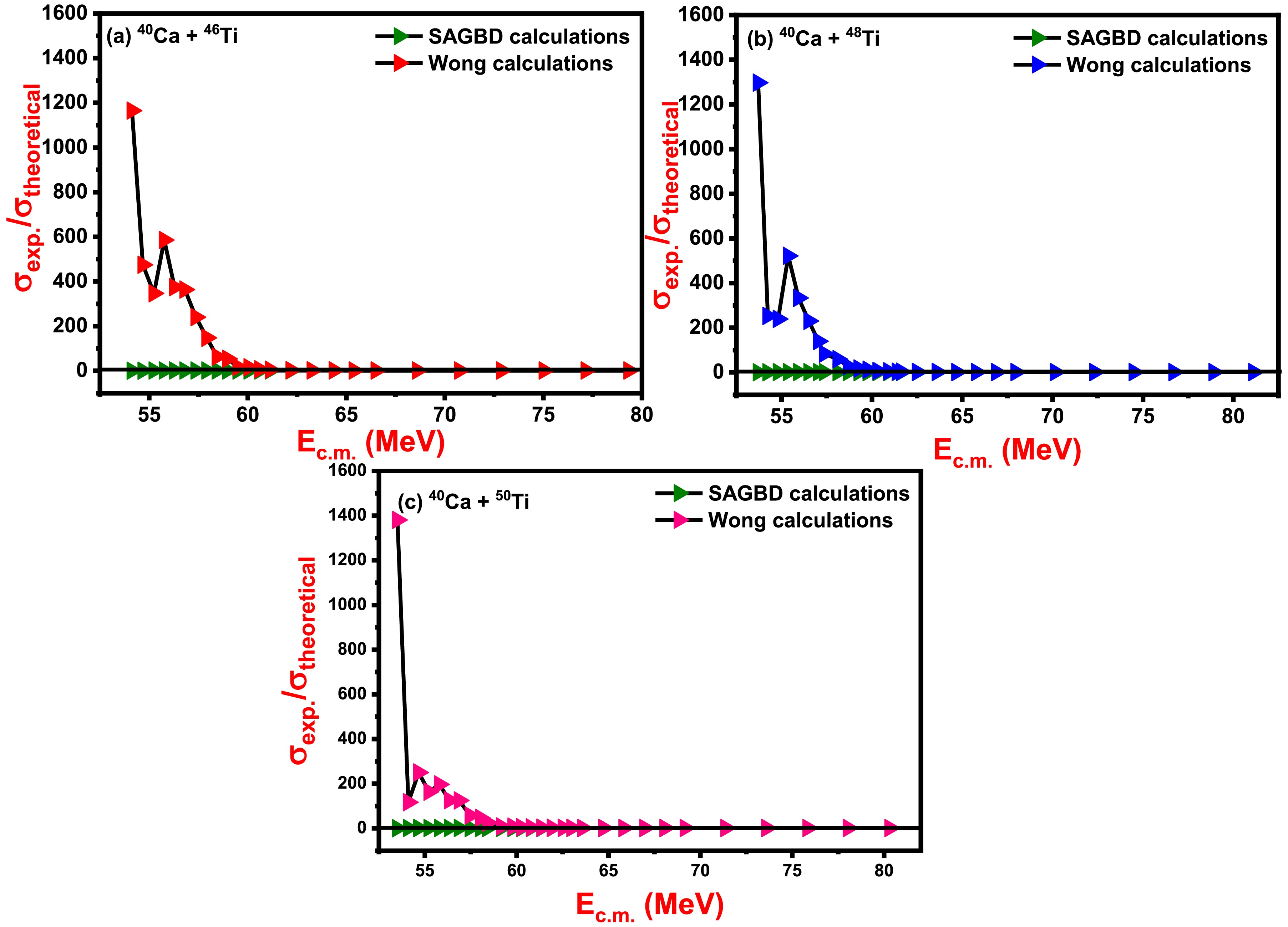
To assess the applicability of the SAGBD model, the ratio of experimental data to theoretically estimated fusion cross-sections for ⁴⁰Ca + ^46,48,50Ti reactions obtained by the simple Wong formula and SAGBD model (with an optimized diffuseness value) is shown in Fig. 6. At above-barrier energies, both Wong and SAGBD calculations keenly reproduce the actual experimental data. However, at below-barrier energies, Wong predictions seemed to be smaller than the experimental data, which further suggests the need for intrinsic degrees of freedom related to the nuclear structure of fusing systems so that the fusion data can be retrieved. For the selected systems, the outcomes due to the SAGBD model and experimental cross-sections, as depicted in Fig. 6, are in agreement with each other. This unambiguously signifies that the Gaussian function used as a weight function of the simple Wong formula considers all the dominant intrinsic channels during the fusion process.

Figure 6.  (color online) Ratio of experimental data to theoretical cross-sections obtained due to Wong formula and SAGBD model for (a) ⁴⁰Ca + ⁴⁶Ti (b) ⁴⁰Ca + ⁴⁸Ti, and (c) ⁴⁰Ca + ⁵⁰Ti systems.

The predictive power of the theoretical approach can be judged by $ {\chi ^2} $-analysis. The SAGBD predictions fairly explained the experimental data of chosen reactions, and their applicability was assessed using $ {\chi ^2} $-analysis. In this regard, the following formula has been used [55−56]:

In the above expression, N and ${E_{\rm c.m.}}$ are the total iterations and experimental energies in the center of mass frame, while fusion cross-sections for experimental and theoretical predictions are denoted by ${\sigma _{\exp }}({E_{\rm c.m.}})$ and ${\sigma _{\rm th}}({E_{\rm c.m.}})$, respectively. The ${\chi ^2}$-analysis also includes the experimental uncertainties of fusion data. ${\chi ^2}$-values for the studied reactions are found to be quite reasonable compared to those obtained from coupled channel description (see Table 6). This unambiguously suggests that the predictions made by the SAGBD model with an optimum diffuseness parameter are consistent with the coupled channel analysis.

Fusion reactions	${\chi ^2}$-value for SAGBD calculations (with an optimum diffuseness)	${\chi ^2}$-value for coupled channel approach
40Ca + 46Ti	2.08	2.33
40Ca + 48Ti	2.35	3.06
40Ca + 50Ti	2.79	3.57

Table 6.  Value of ${\chi ^2}$ calculated for SAGBD calculations with optimal diffuseness for given reactions.

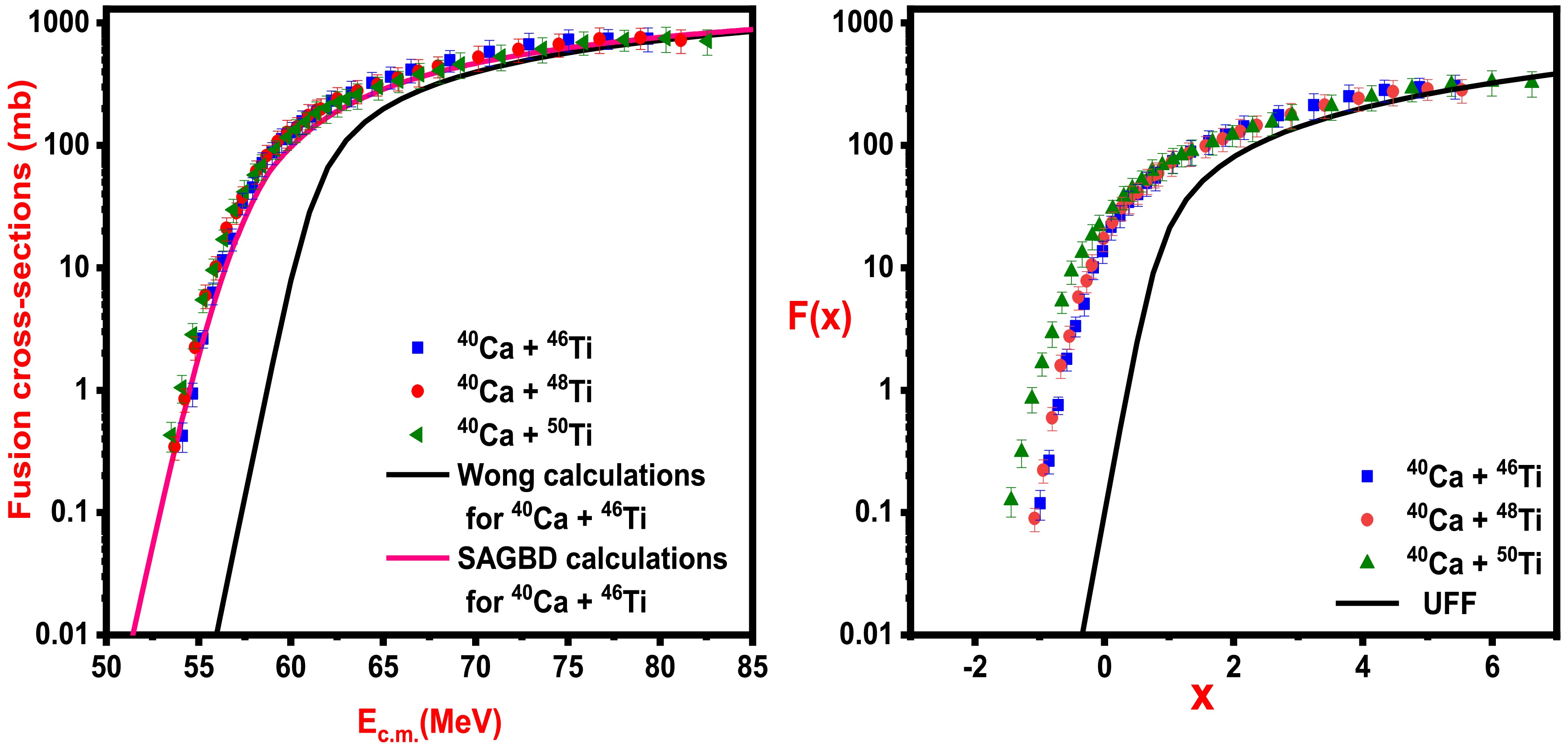
In Fig. 7, a comparison of fusion data for ⁴⁰Ca + ^46,48,50Ti reactions with the fusion cross-sections of ⁴⁰Ca + ⁴⁶Ti reaction predicted by theoretical models (Wong formula and SAGBD model with ${a_0} = 0.76\;{\rm{fm}}$) is shown at normal scale (Fig. 7(a)) and reduced scale (Fig. 7(b)). When a common projectile is incident on isotopes of the given target, larger sub-barrier fusion enhancement is seen for heavier isotopes, and this fact can be correlated with the increase in neutron richness for the heavier Ti-isotope. With an increase in neutrons, the probability of neutron transfer channel with Q-value also increases. As a result, the fusion probability as well as fusion cross-sections are found to be enhanced in magnitude, particularly at below-barrier energies. SAGBD predictions reasonably describe the fusion dynamics of ⁴⁰Ca + ^46,48,50Ti reactions, and the channel coupling parameter for the ⁴⁰Ca + ⁵⁰Ti system is larger (i.e., ${\lambda ^{\rm SAGBD}} = 3.46$) in comparison to that of other studied systems, i.e., ${\lambda ^{\rm SAGBD}} = 3.38$ for ⁴⁰Ca+⁴⁶Ti and ${\lambda ^{\rm SAGBD}} = $ 3.44 for ⁴⁰Ca + ⁴⁸Ti. This clearly suggests that the heaviest target isotope displayed larger sub-barrier fusion enhancement as the ⁵⁰Ti-isotope is enriched in neutrons in comparison to ^46,48Ti-isotopes. In a similar sense, sub-barrier fusion enhancement of the ⁴⁰Ca + ⁴⁸Ti reaction is larger than that of the ⁴⁰Ca + ⁴⁶Ti reaction. Figure 7 unambiguously identifies that neutron transfer coupling dominates over inelastic surface vibrational couplings in the ⁵⁰Ti-isotope, leading to larger sub-barrier fusion enhancement of ⁵⁰Ti-isotopes relative to ^46,48Ti-isotopes. For clarity, the fusion cross-section data of given reactions are compared with the universal fusion function (UFF), as shown inFig. 7(b).

Figure 7.  (color online) Fusion cross-sections of studied reactions at normal and reduced scales.

In addition to the above predictions, entrance channel mass asymmetry $ \eta = \dfrac{{\left| {{A_P} - {A_T}} \right|}}{{\left| {{A_P} + {A_T}} \right|}} $ for ⁴⁰Ca + ^46,48,50Ti reactions is defined as ${\eta _{^{40}{\rm Ca}{\text{ }}{ + ^{50}}{\rm Ti}}} = 0.111$, ${\eta _{^{40}{\rm Ca}{\text{ }}{ + ^{48}}{\rm Ti}}} = 0.090$, and ${\eta _{^{40}{\rm Ca}{\text{ }}{ + ^{46}}{\rm Ti}}} = 0.069$, following an increasing trend from lighter to heavier Ti-isotopes. In the literature [48], it was emphasized that sub-barrier fusion enhancement is favoured by larger $ \eta $ (entrance channel mass asymmetry). Therefore, for ⁴⁰Ca + ^46,48,50Ti reactions, the sub-barrier fusion enhancement follows a similar trend as that of variations of $ \eta $, as evident from Fig. 7. The coupled channel calculations and SAGBD-based calculations clearly identified the target isotopic dependence of sub-barrier fusion enhancement of the studied systems.

For ⁴⁰Ca + ^46,48,50Ti systems, the simple Wong formula does not reproduce the experimental data of given systems as it does not consider the intrinsic degrees of freedom of collision partners. To overcome the discrepancies of the Wong formula, a choice of deformed nuclear potential is considered with Wong formula, which is called the deformed Wong model and is considered for the theoretical estimations for given systems. In the deformed Wong model, the quadrupole deformation of both fusing pairs is taken, but such calculations do not generate the desired outputs. Hence, an additional radius parameter $\Delta R$ (value of $\Delta R$ is optimized for chosen reactions by fitting the fusion data) with quadrupole deformation of both nuclei is taken in the deformed Wong model. Using an optimized $\Delta R$ and quadrupole deformation, fusion data are regenerated well. In the SAGBD model, total fusion cross-sections are obtained by weighting Gaussian function to the Wong formula. Further, to assess the sensitivity of fusion cross-section data of given reactions with respect to potential parameters, Winther and Akyüz-Winther diffuseness are used within the SAGBD model. Using these parameterizations in the SAGBD model, theoretical outcomes of fusion cross-sections as well as barrier distributions turned out to be enhanced relative to the predictions due to the simple Wong formula but unable to recover experimental data in sub-barrier energy regions. Using an optimized diffuseness parameter (which is larger than Winther and Akyüz-Winther diffuseness) in the SAGBD model, fusion cross-sections and barrier distributions are calculated, and such calculations fairly reproduced experimental data of studied systems. Further, the channel coupling parameter ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$ for ⁴⁰Ca + ⁴⁶Ti are 3.38 and 5.51% of ${V_{CB}}$, respectively (${\lambda ^{\rm SAGBD}} = 3.44$, ${V_{\rm CBRED}} = 5.62{\text{%}}$ of ${V_{CB}}$ for ⁴⁰Ca + ⁴⁸Ti and ${\lambda ^{\rm SAGBD}} = 3.46$, ${V_{\rm CBRED}} = 5.73{\text{%}}$ of ${V_{CB}}$ for ⁴⁰Ca + ⁵⁰Ti), clearly demonstrating that the intrinsic degrees of freedom of collision partners are important for fusion enhancement of ⁴⁰Ca + ^46,48,50Ti reactions. The trend of increasing ${\lambda ^{\rm SAGBD}}$ and ${V_{\rm CBRED}}$ for the given reactions unambiguously identifies greater sub-barrier fusion enhancement of ⁴⁰Ca + ⁵⁰Ti reactions over ⁴⁰Ca + ^46,48Ti reactions, thereby suggesting the dominance of neutron transfer couplings over inelastic surface vibrational couplings. On a similar ground, one can say that sub-barrier fusion enhancement of the ⁴⁰Ca + ⁴⁸Ti reaction appears to be enhanced compared to that of the ⁴⁰Ca + ⁴⁶Ti reaction.

The fusion dynamics of ⁴⁰Ca + ^46,48,50Ti systems have also been explored within the coupled channel approach using CCFULL code. For these reactions, coupling to individual 2⁺ and 3^– vibrational states of projectile and target do not reproduce the experimental data. The considerations of individual single-phonon 2⁺ and 3^– vibrational states of both fusing pairs as well as their mutual coupling states like $({2^ + } \otimes {3^ - })$ fairly describe the fusion data of ⁴⁰Ca + ^46,48Ti reactions at near- and below-barrier energy regions. However, for ⁴⁰Ca + ⁵⁰Ti reactions, the small discrepancies between coupled channel calculations obtained by considering inelastic surface excitations 2⁺ and 3^– of both fusing systems and fusion data can be correlated with a pair neutron transfer channel with positive Q-value. In the present coupled channel calculations, such a neutron transfer channel is not incorporated in the theoretical outcomes. Further, the ratio of experimental and theoretical fusion cross-sections was analyzed for SAGBD- and Wong-based calculations, which unambiguously suggested that the theoretical outcomes due to the SAGBD model satisfactorily explain fusion and barrier distributions data of ⁴⁰Ca + ^46,48,50Ti reactions. The results of the SAGBD model and deformed Wong model with an additional radius parameter $\Delta R$ are found to be analogous to those of the coupled channel approach. This suggests that the Gaussian function brings similar barrier modification effects, as inferred from the couplings to multiphonon states of colliding nuclei and/or nucleon transfer channel during the fusion process. Furthermore, the present work suggested that ⁴⁰Ca exhibits strong octupole vibrations that significantly influence the fusion yields, and hence, ⁴⁰Ca + ^46,48,50Ti reactions show target isotopic dependence of sub-barrier fusion enhancement. The increasing trend of entrance channel mass asymmetry with an increase of neutron richness of target isotope favors the fusion process at near- and sub-barrier energies.