Near-barrier fusion of ^16,18O + ⁵⁰Cr: The role of positive Q-value two-neutron stripping channel

Heavy-ion fusion at energies near and below the Coulomb barrier ($ V_{\mathrm{B}} $) is connected to the basic quantum problems of tunneling and coupled-channels (CC) effect, wherein CC effect is the kernel problem in sub-barrier heavy-ion fusion, as generally existing in many branches of physics and chemistry [1]. Fusion mechanism of heavy-ions is also related to super-heavy element synthesization and celestial phenomena like super-ray burst occurring in the neutron star crust [2]. Therefore, it has always been a hot topic of both experimental and theoretical sides [3−13], since the discovery of the so-called sub-barrier fusion enhancement (up to few orders of magnitude) due to the static deformation effect in 1978 [11].

Heavy-ion fusion is the complete amalgamation of projectile into target nucleus, with coming to equilibration in all degrees of freedom, to form an excited compound nucleus (CN). Complete fusion above the barrier can be explained by a classical picture of a Weisskopf formulation [14, 15]. The classical formula for fusion cross section ($ \sigma_{\mathrm{Fus}} $) $ \sigma_{\mathrm{Fus}} $ = $ \pi R_{\mathrm{B}}^2 $(1 - $ V_{\mathrm{B}} $/$ E_{\mathrm{cm}} $) was used to extract the barrier height $ V_{\mathrm{B}} $ and position $ R_{\mathrm{B}} $ by using the measured fusion cross sections of the non-heavy tightly-bound systems at energies well above the barrier [16].

For the lighter systems, sub-barrier fusion process can be roughly seen as an inverse process of α-decay [17] or low-energy fission wherein the Hill-Wheeler penetration formula based on the proposed parabolic potential shape [18]. Later, Wong's formula was proposed to calculate the near-barrier fusion cross section with Hill-Wheeler penetration formula, considering the static deformation of the reactants [19]. All the ideas mentioned above belong to the category of the one-dimensional barrier penetration model (1D-BPM).

When the reaction system becomes heavier, CC effect becomes dominant in the sub-barrier fusion. As well known, sub-barrier fusion cross section is generally mediated by strong couplings to nuclear rotational states [20], vibrational states [21], and nucleon transfer [22], that is a phenomenon of coupling-aided tunneling. The couplings could lead to barrier splitting and then form a multi-dimensional barrier distribution [23], wherein the reduced barrier lower than the original single-barrier corresponds to the increased fusion cross section. Up to now, the effect of coupling to transfer channels is still not consistent experimentally. At the same time, it is still difficult to take this effect into account self-consistently in theory, although the microscopic theories of coupled reaction channels [24] and time-dependent Hartree-Fock [25] have been used to consider the effect of nucleon transfers in calculating the fusion cross sections.

The CC effect potentially correlated to nucleon transfers was first discovered in $ ^{58} {\rm{Ni}}$ + $ ^{64} {\rm{Ni}}$ using the comparative experimental study for the $ ^{58,64} {\rm{Ni}}$ + $ ^{58,64} {\rm{Ni}}$ systems, which set a precedent to extract the nucleon transfer effect experimentally [26]. A kinematic neutron-transfer Q-value effect was then proposed to explain the enhancement in a model-independent way [22], wherein the intermediate positive Q-value neutron transfer channels (PQNT), and also the indistinguishable effective ground-state positive Q-value ($ Q^{\mathrm{eff}} $) proton transfer (PQPT) channels could increase the penetrability in the two-step non-dynamical picture. $ Q^{\mathrm{eff}} $ is the ground-state Q-value plus the Coulomb-barrier difference between the incoming channel ($ V_{\mathrm{B}}^{\mathrm{in}} $) and the intermediate transfer channel ($ V_{\mathrm{B}}^{\mathrm{tr}} $), that is $ Q^{\mathrm{eff}} $ = $ Q^{\mathrm{gs}} $ + ($ V_{\mathrm{B}}^{\mathrm{in}} $ - $ V_{\mathrm{B}}^{\mathrm{tr}} $).

Considering the large neutron transfer cross section at near-barrier energies, the prevailing view is that coupling to positive Q-value neutron transfer channels should play an important role in sub-barrier fusion of heavier system such as $ ^{40} {\rm{Ca}}$ + $ ^{48} {\rm{Ca}}$ [27, 28] and $ ^{40} {\rm{Ca}}$ + $ ^{96} {\rm{Zr}}$ [29]. However, the systems that were once claimed to have strong neutron transfer effect, such as $ ^{40} {\rm{Ca}}$ + $ ^{48} {\rm{Ca}}$, $ ^{96} {\rm{Zr}}$, $ ^{58} {\rm{Ni}}$ + $ ^{64} {\rm{Ni}}$, also have effective ground-state positive Q-value two-proton stripping channels (+7.57 MeV, +7.96 MeV, +2.66 MeV) at the same time. The potential role of proton stripping in sub-barrier fusion enhancement should not be arbitrarily ignored, and was also proposed such as in Ref. [30]. The definitions of ”pickup” and ”stripping” reactions are given in terms of transfer to or from the lighter partner of the two reactants in the reaction as conventionally [31]. Therefore, despite many experimental and theoretical [32−39] studies, the dynamics of neutron-transfer-mediated sub-barrier fusion has not yet been well revealed [6]. From the above analysis, to study fusion of the systems without such proton-stripping channels is helpful to unveil the critical reaction mechanism.

The neutron-rich $ ^{18} {\rm{O}}$-induced fusion is an ideal selection [40−44] for this kind of study considering the positive Q-value neutron stripping due to the N = 8 magic number of $ ^{16} {\rm{O}}$ core, and inhibited proton-stripping due to both p-shell closure for Z = 8 magic number. $ ^{18} {\rm{O}}$ projectile can be seen as a core plus two loosely-bound valence neutrons in a ”di-neutron” configuration outside the tightly-bound $ ^{16} {\rm{O}}$ core [45]. Therefore, $ ^{18} {\rm{O}}$ can be considered as a good reservoir of neutron-pair to excite the target-pairing vibration modes [46, 47, 49] and may lead to 2n-transfer cross section as high as 1n-transfer [48]. The earlier measurement for fusion of $ ^{18} {\rm{O}}$ + $ ^A {\rm{Sn}}$ and our measured $ ^{18} {\rm{O}}$ + $ ^{74} {\rm{Ge}}$ show no enhancement [41, 43], While, fusion of $ ^{18} {\rm{O}}$ + $ ^{58} {\rm{Ni}}$ was claimed to show obvious enhancement [50] and was once used as a benchmark for theories [37]. In order to further study the fusion behavior of $ ^{18} {\rm{O}}$-induced systems with bigger positive Q-value 2n transfer channels and establish a systematic evolution of this effect, further measurements for fusion of $ ^{18} {\rm{O}}$ with different target nuclei are highly needed.

Usually, in order to single out the collective excitations and highlight the nucleon transfer effect, systems with lower $ Z_{\mathrm{P}} $$ Z_{\mathrm{T}} $ (weak inelastic coupling effect) and large ground state Q-values for nucleon transfers is ideal for obtaining quantitative information. This is the case for the 1n and 2n stripping channels whose exothermic Q-values are +1.22 and +9.11 MeV for $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$. This system, with both high $ Q^{\mathrm{gs}}_{-2n} $-value +9.11 MeV and $ Q^{\mathrm{gs}}_{-2n} $/$ V_{\mathrm{B}} $ $ \sim $ 0.33, was measured to highlight its potential role at energies near and below the Coulomb barrier. Fusion of $ ^{16} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$, without positive Q-value neutron transfers, was also measured as a reference.

The collimated $ ^{16,18} {\rm{O}}$ (charge state q = 5$ ^+ $) beams were delivered at intensities ranging from 2 to 20 pnA by the HI-13 tandem accelerator at the China Institute of Atomic Energy (CIAE), Beijing. Measurements of the fusion evaporation residuals (ER) by using an electrostatic deflector [51] have been conducted for the $ ^{16,18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ reactions at energies near and below the Coulomb barriers. The beam energies for collimated $ ^{16} {\rm{O}}$ were varied across the range of 33 MeV (0.89 $ V_{\mathrm{B}} $) to 60 MeV (1.63 $ V_{\mathrm{B}} $) and for collimated $ ^{18} {\rm{O}}$ were varied across the range of 31 MeV (0.84 $ V_{\mathrm{B}} $) to 55 MeV (1.48 $ V_{\mathrm{B}} $), with larger steps 2.4$ / $1.2 MeV at higher energies and a smaller step 0.6 MeV at lower energies. The adjustments were made exclusively in a downward direction, starting from the highest energy, to minimize magnetic hysteresis. The $ ^{50} {\rm{Cr}}$ target, which is 97.40% isotope enriched with a diameter of 3 mm and thickness 70 μg/cm², were sputtered onto carbon foils with a thickness of 23 μg/cm². Four silicon (Si) detectors were symmetrically positioned at the forward angle $ \pm 17 ^\circ $ relative to the beam direction covering both the right-left and up-down orientations, for measuring Rutherford scattering to monitor the beam condition and normalize the fusion cross section.

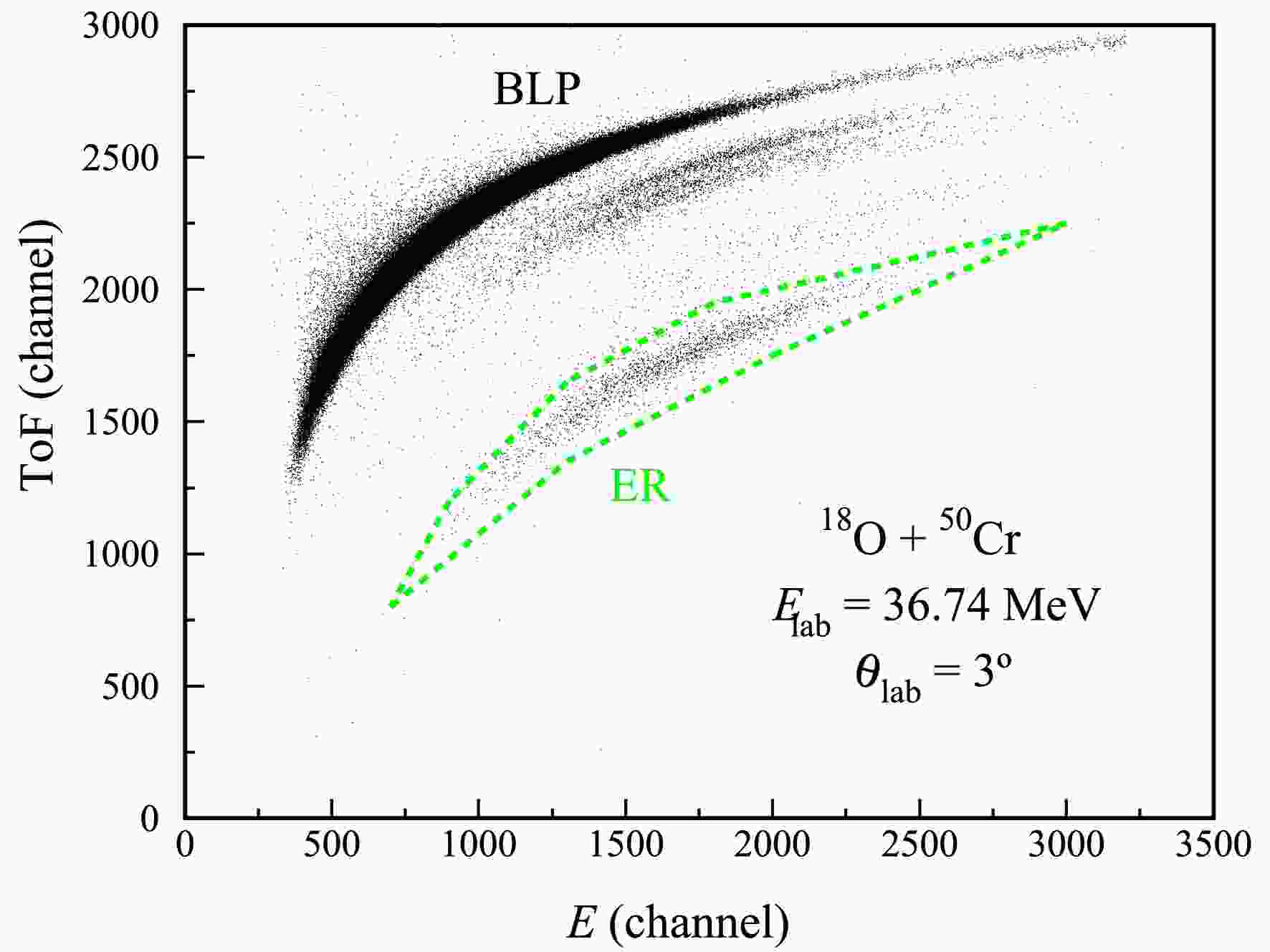
ER were effectively separated from the beam-like particles (BLP) at forward angles, relative to the beam direction, based on the electrical rigidity E/q of the reaction products by using two pairs of electrodes. The reaction products corresponds to an opening angle of $ \theta_{\mathrm{lab}} $ = $ \pm 0.38 ^\circ $ can enter the electric field region, selected by an entrance collimator with a diameter of 2.5 mm at a distance of 19.0 cm downstream to the target. A carbon foil with a thickness of 10 μg/cm² on the collimator was employed to reset the atomic charge state distribution through the internal conversion process along the ion path. Subsequently, they were identified via the two-dimensional E vs time-of-flight (ToF) spectrum, wherein the detector telescope consists of two microchannel plate (MCP) detectors for measuring ToF and a quadrant silicon detector with an active area of 50 $ \times $ 50 mm² for energy measurements. The quadrant silicon detector was used also for monitoring the spatial distribution of ER and hence ensuring the optimum electric field used. A typical two-dimensional E-ToF spectrum, for separating the ER from the BLP-products measured at 3$ ^\circ $ for the $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system at $ E_{\mathrm{lab}} $ = 36.74 MeV (0.99 $ V_{\mathrm{B}} $), is shown in Fig. 1, wherein the ER and BLP can be clearly distinguished.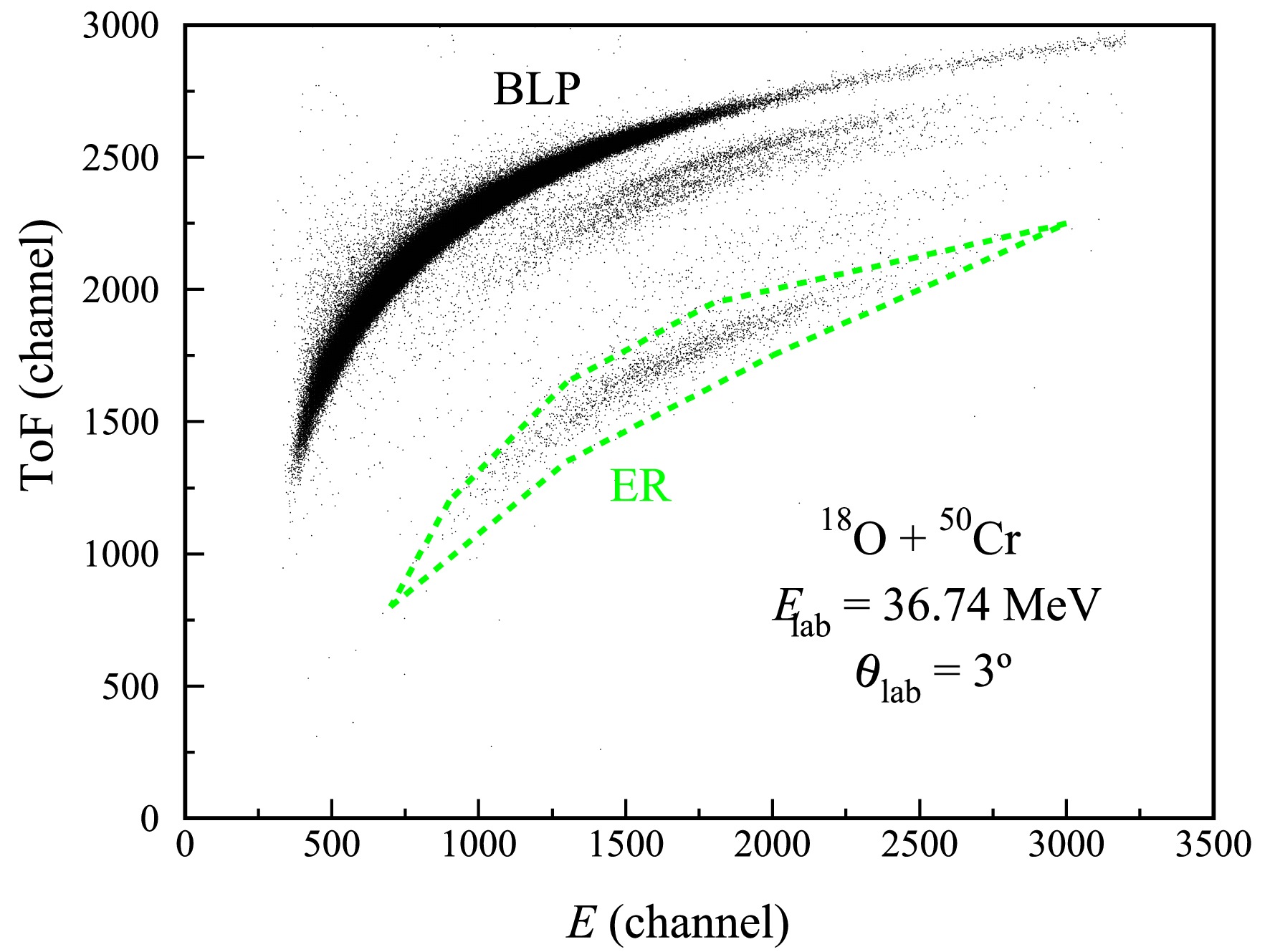

Figure 1.  (color online) A typical two-dimensional E-ToF spectrum for separating the ER from the scattered beam-like products measured at $3^\circ$ for the $^{18}{\rm{O}}$ + $^{50}{\rm{Cr}}$ system at $E_{\mathrm{lab}}$ = 36.74 MeV (0.99 $V_{\mathrm{B}}$). The group of ER corresponds to fusion evaporation residue events and BLP means the beam-like particles.

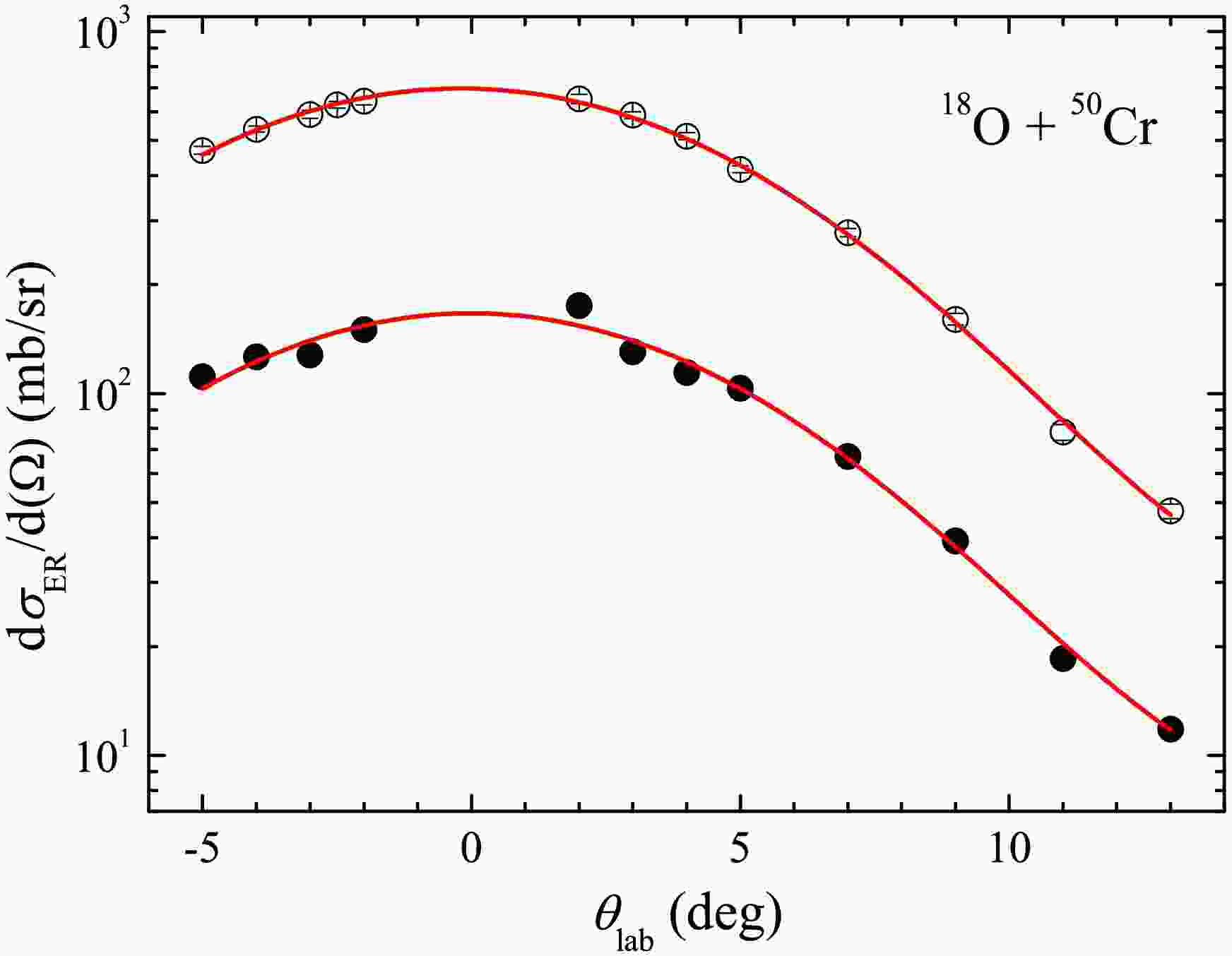
The angular distributions of the ER were measured for $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ at $ E_{\mathrm{lab}} $ = 47.59 and 38.55 MeV, respectively, in the range $ \theta_{\mathrm{lab}} $ = -5$ ^\circ $ to 13$ ^\circ $ with step $ \theta_{\mathrm{Lab}} $ = 1$ ^\circ $ or 2$ ^\circ $, as shown by the points with sole representation of the statistical errors in Fig. 2, wherein the error bar is smaller than the symbol size. The lines correspond to the Gaussian fits. Since fission of the excited CN can be neglected for such light systems, the measured ER cross sections $ \sigma_{\mathrm{ER}} $ are equal to $ \sigma_{\mathrm{Fus}} $. The total fusion cross section $ \sigma_{\mathrm{Fus}} $ is derived by integrating the angular distributions, wherein corrections were made for the transmission efficiency.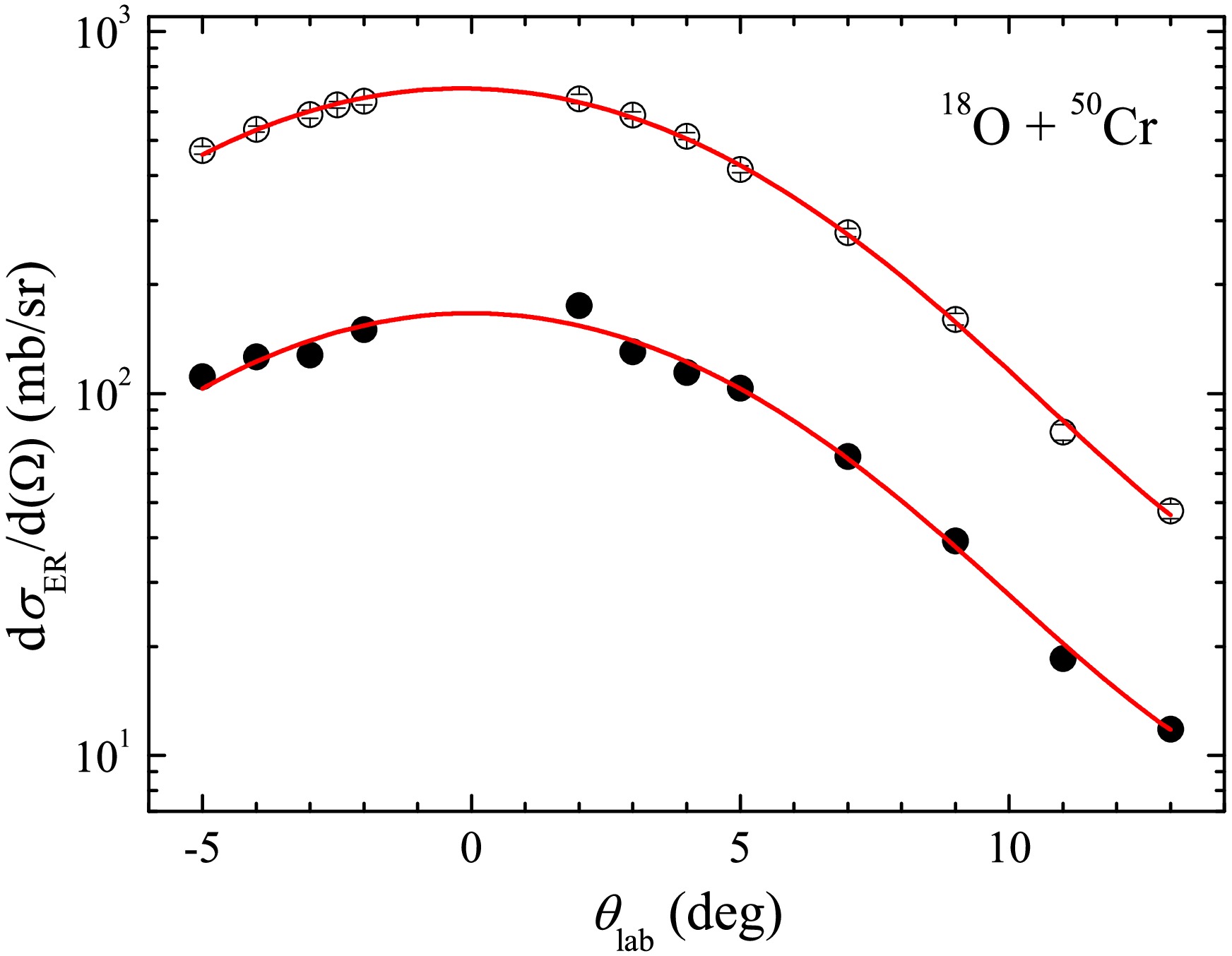

Figure 2.  (color online) The angular distributions of the ER measured for $^{18}{\rm{O}}$ + $^{50}{\rm{Cr}}$ at $E_{\mathrm{lab}}$ = 47.59 (hollow circles) and 38.55 MeV (solid circles). The error bars are purely from statistics and usually smaller than the point size. The two curves are the Gaussian fits.

The two measured angular distributions show a small variation in shape with energy, characterized by a full width at half maximum (FWHM) of the Gaussian fit that decreases from 12.1$ ^\circ $ to 11.7$ ^\circ $. These distributions are in accordance with the predictions by the code PACE2 [52]. Therefore, the theoretical angular distributions were employed to calculate $ \sigma_{\mathrm{Fus}} $ for other energies, utilizing the measured fusion differential cross sections at a certain angle. More details can be found in Ref. [51].

The integrated fusion cross sections for the $ ^{16} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ and $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ systems as a function of the center-of-mass frame energy ($ E_{\mathrm{cm}} $) are shown in Figs. 3 and 4 by the hollow points, respectively. The energy has been corrected to account for the energy loss in targets and carbon backing (faced to the beams). The statistical uncertainties are approximately ±1.0% for the higher and intermediate energy-points, increasing to about ±31% for the lowest energy-point.

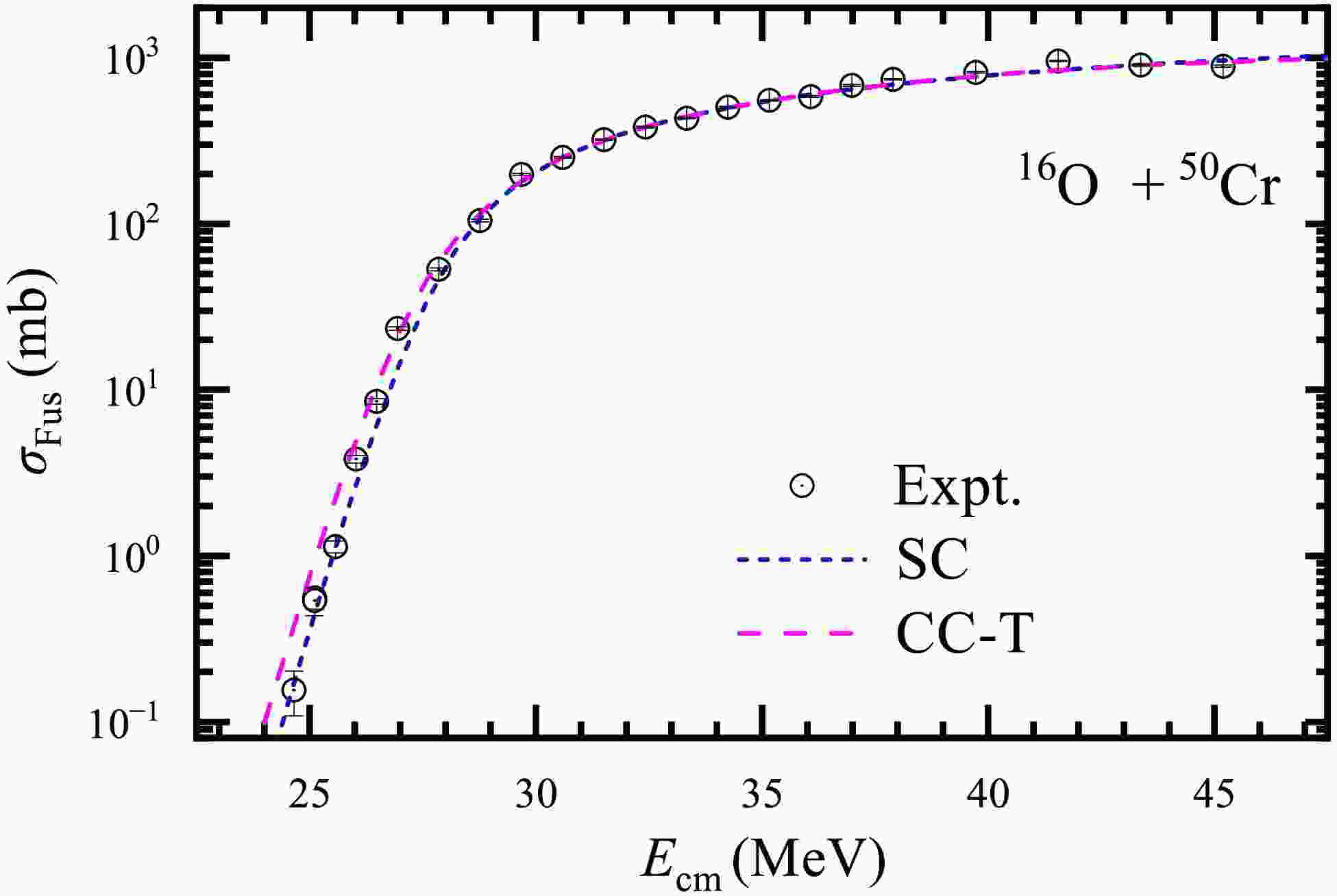
Figure 3.  (Color online) The experimental fusion excitation function (hollow circles) and the calculated results for the $^{16}{\rm{O}}$ + $^{50}{\rm{Cr}}$ system.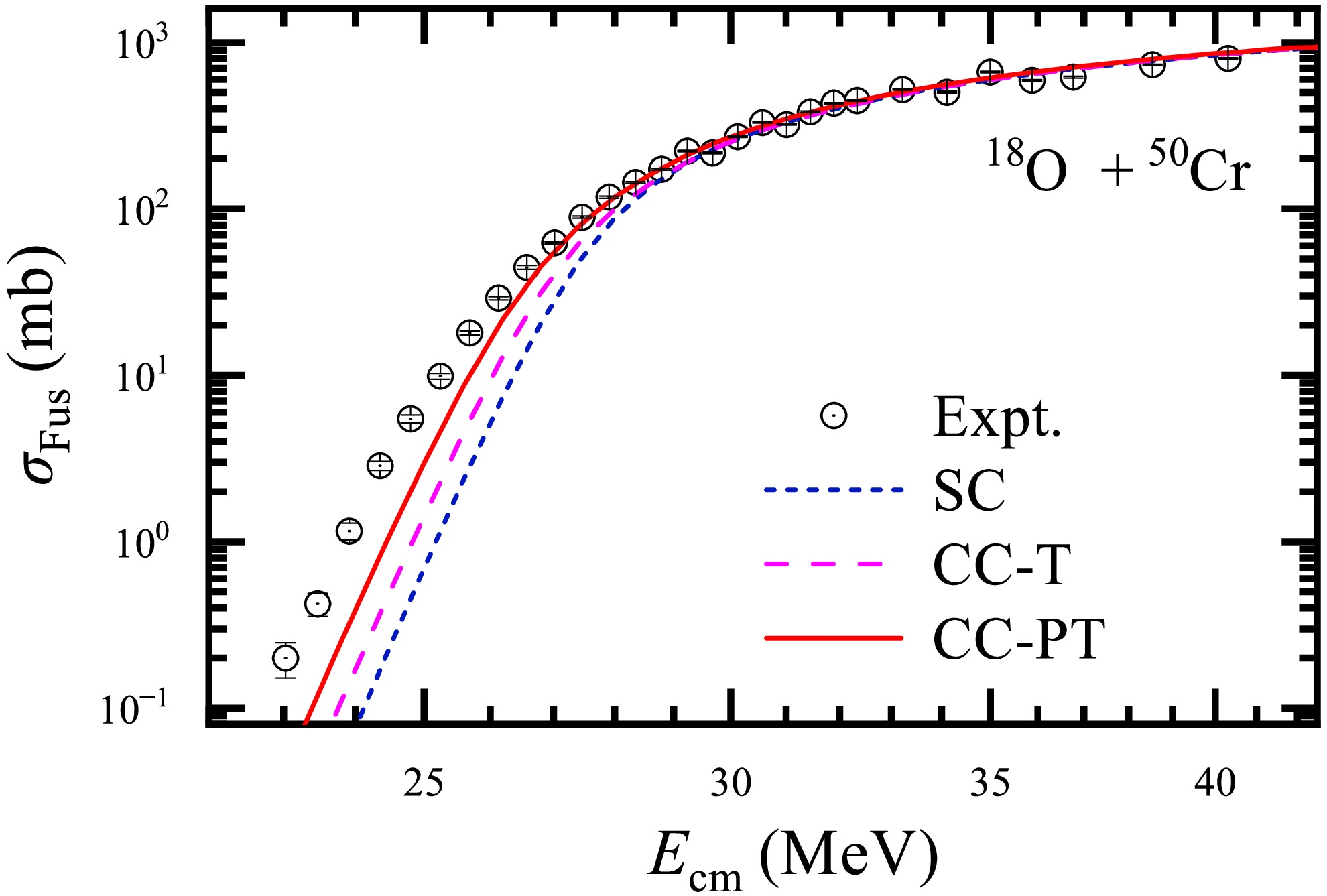

Figure 4.  (Color online) The experimental fusion excitation function (hollow circles) and the calculated results for the $^{18}{\rm{O}}$ + $^{50}{\rm{Cr}}$ system.

The analysis of the fusion data was conducted using the code CCFULL [53], which incorporates all-order nonlinear couplings and uses the incoming wave boundary condition at the minimum of the potential pocket (inside the Coulomb barrier). The excitation energies $ E_{\mathrm{x}} $, spins and parities $ \lambda^{\pi} $, and deformation parameters $ \beta_{\lambda} $ [54, 55] of the low-lying collective excitation states for $ ^{16,18} {\rm{O}}$ and $ ^{50} {\rm{Cr}}$ are shown in Table 1. The effects of coupling to low-lying collective excitation states of the reactants were considered, and the standard Akyüz-Winther (AW) nuclear potential [56] was adopted here. The corresponding parameters together with those of the uncoupled potentials used in the present CC calculations are reported in Table 2.

Nucleus	$E_{\mathrm{2^+}}$/MeV	$\beta_2$	$E_{\mathrm{3^-}}$/MeV	$\beta_3$
$^{16}{\rm{O}}$			6.130
$^{18}{\rm{O}}$	1.982	0.355
$^{50}{\rm{Cr}}$	0.783	0.293	4.052	0.095

Table 1.  Excitation energies $E_{\mathrm{x}}$, spins and parities $\lambda^{\pi}$, and deformation parameters $\beta_{\lambda}$ [54, 55] of the low-lying collective excitation states for $^{16,18}{\rm{O}}$ and $^{50}{\rm{Cr}}$.

System	$V_0$/MeV	$R_0$/fm	a/fm	$V_{\mathrm{B}}$/MeV	$R_{\mathrm{B}}$/fm	ħω/MeV
$^{16}{\rm{O}}$ + $^{50}{\rm{Cr}}$	52.713	1.171	0.631	27.723	9.268	3.700
$^{18}{\rm{O}}$ + $^{50}{\rm{Cr}}$	53.879	1.171	0.635	27.256	9.437	3.480

Table 2.  Parameters of the Akyüz-Winther potential [56] and barrier heights, radii, and curvatures of the uncoupled potentials for $^{16,18}{\rm{O}}$ + $^{50}{\rm{Cr}}$ employed in the CC calculations.

The first excitation state $ 3^- $ of $ ^{16} {\rm{O}}$ with higher excitation energy 6.13 MeV, larger than the barrier curvature, should not be explicitly taken into account in the CC calculations due to the adiabatic effect [57, 58]. The nucleus $ ^{50} {\rm{Cr}}$ exhibits excellent vibrational characteristics, with its lowest 2$ ^+ $ state located at 783.3 keV. For the $ ^{16} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system without positive Q-value nucleon transfer channels, the result of the single-channel (SC) calculation is depicted by the short-dashed line, as shown in Fig. 3. The calculations incorporating the low-lying vibrational 2$ _1^+ $ one-phonon state of $ ^{50} {\rm{Cr}}$ (CC-T), without considering coupling to the collective excitations of $ ^{16} {\rm{O}}$, is represented by the long-dashed line. The results indicate that both the SC and CC-T calculations reproduce the fusion excitation function quite well within the experimental uncertainties, consistent with the expected smaller role of coupling to inelastic channels due to the smaller coupling strength β$ Z_{\mathrm{P}} $$ Z_{\mathrm{T}} $ for the lighter systems.

For the $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system, the results of the SC calculation (short-dashed line) obviously under-estimates the sub-barrier fusion cross sections, as shown shown in Fig. 4. The CC calculated result CC-T (long-dashed line), which includes the 2$ _1^+ $ one-phonon state of $ ^{50} {\rm{Cr}}$ is still less than experimental result at energies below the barrier. The CC calculated result CC-PT (solid line), further including the 2$ _1^+ $ one-phonon state of $ ^{18} {\rm{O}}$ is still, but very modestly, smaller than the experimental ones at energies below the barrier, leaving little room for other effects mostly related to nucleon transfers for $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ or couplings to multi-phonon states [59].

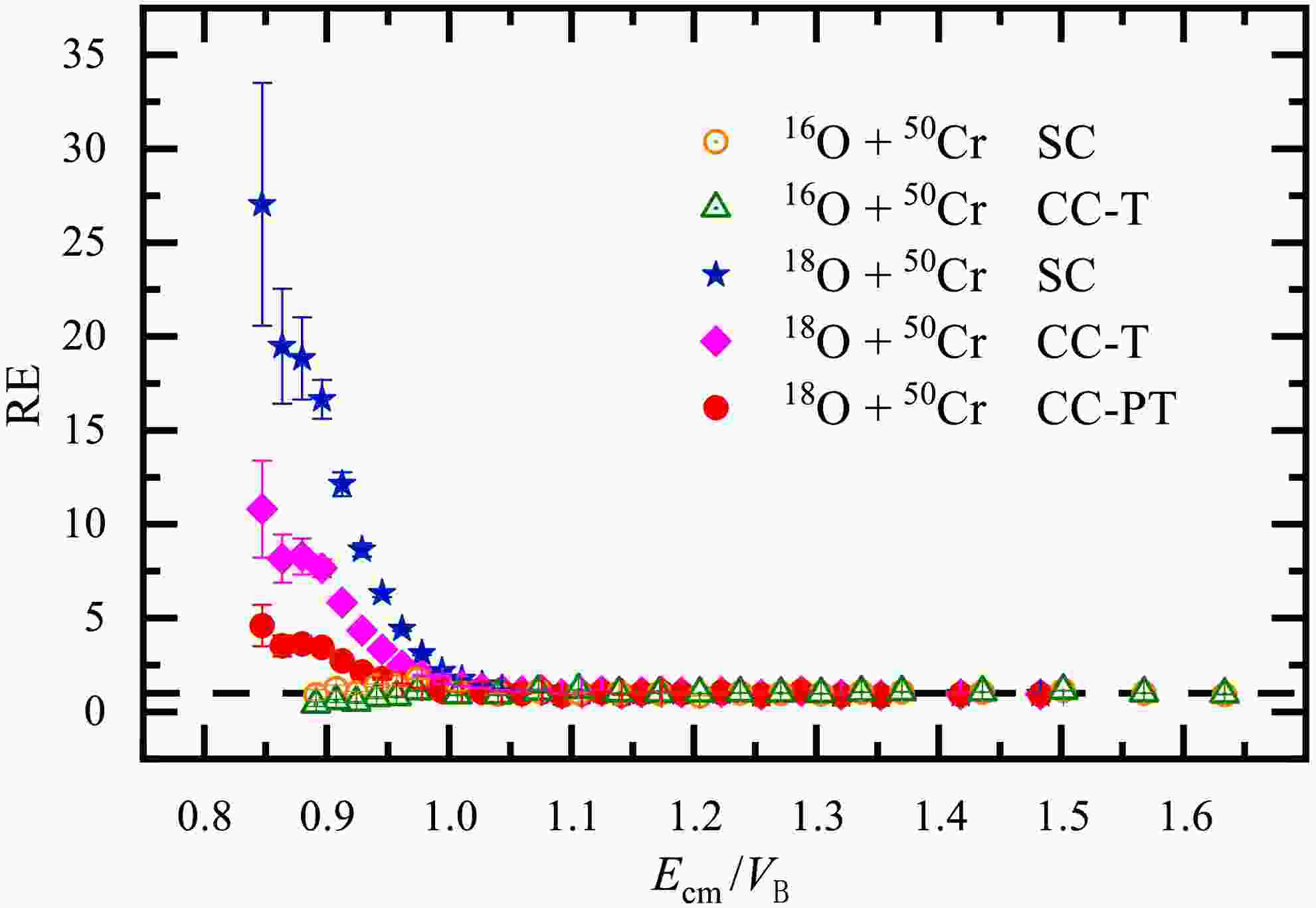
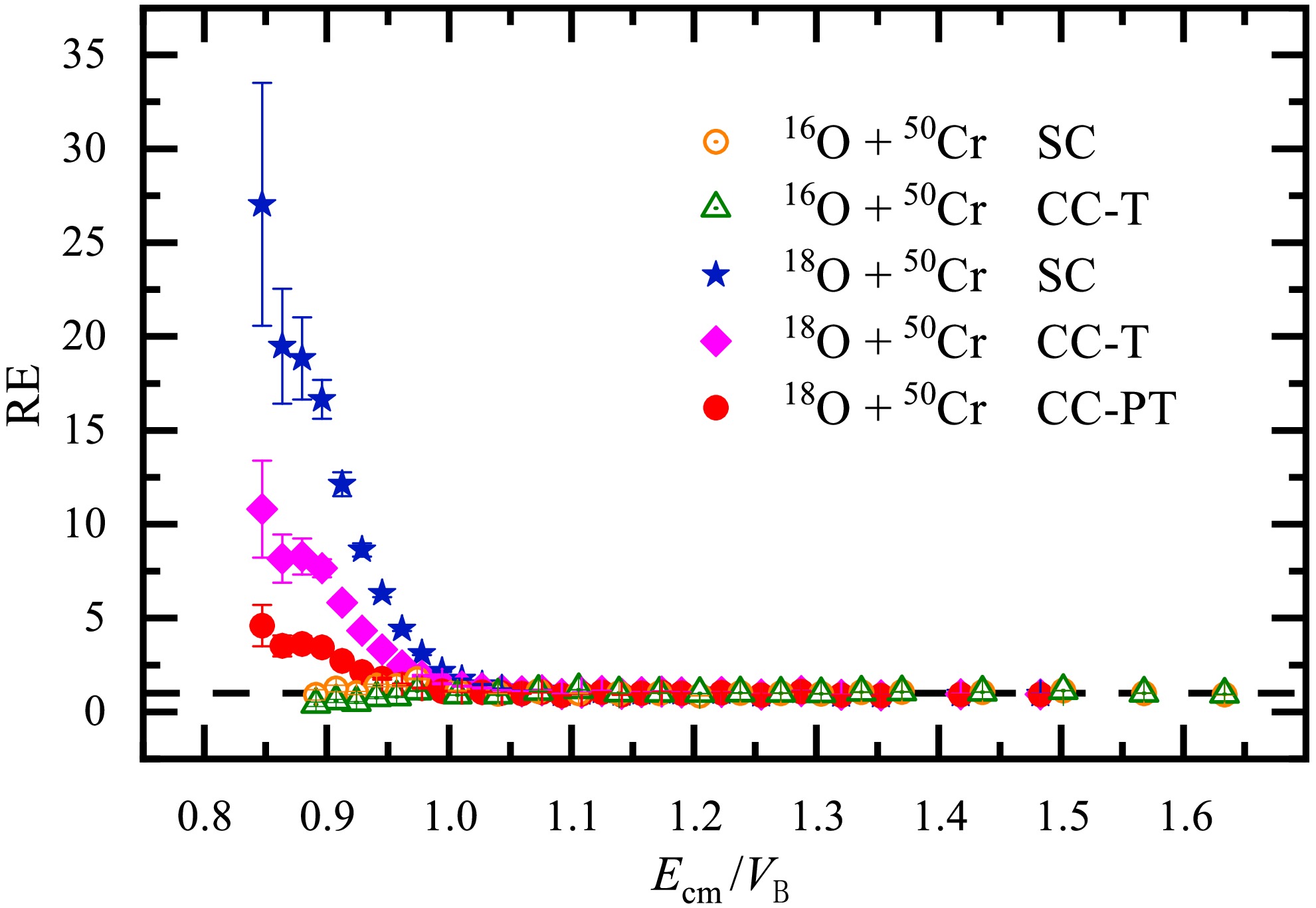
It is important to note that the $ ^{16} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system, which is expected to have no PQNT effects, can be used as a benchmark. The calculation scheme for the inelastic coupling channels of $ ^{50} {\rm{Cr}}$ in the $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system is the same as that for the $ ^{16} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system, allowing for a more reliable comparison of the residual enhancement (RE) due to nucleon transfer effect, which was defined as the ratio of the experimental fusion cross section to the calculated one, expressed as RE = $ \sigma_{\mathrm{Expt}} $/$ \sigma_{\mathrm{CC}} $ [60]. The variation of RE with the reduced energy $ E_{\mathrm{cm}} $/$ V_{\mathrm{B}} $ for the $ ^{16,18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ systems is shown in Fig. 5. For the $ ^{16} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ system, RE for both the SC (hollow circles) and CC-T (hollow triangles) calculations keeps almost unity at the whole measured energy region, meaning a good reference for highlighting the coupling effect to neutron transfer channels in fusion of $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$. For $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$, all the SC (stars), CC-T (diamonds), and CC-PT (solid circles) calculated results deviate from unity at energies below the Coulomb barrier. While, the RE of CC-PT calculation shows only subtle deviation, meaning little potential role of the positive Q-value 2n-stripping channel effect in the measured sub-barrier energy region despite its big $ Q^{\mathrm{gs}}_{-2n} $-value and $ Q^{\mathrm{gs}}_{-2n} $/$ V_{\mathrm{B}} $-value for $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$.

Figure 5.  (Color online) The variation of RE with the reduced energy $E_{\mathrm{cm}}$/$V_{\mathrm{B}}$ for the $^{16,18}{\rm{O}}$ + $^{50}{\rm{Cr}}$ systems.

The present comparative study for $ ^{16,18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ suggests that positive Q-value 2n-stripping channel in $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ does not enhance the sub-barrier fusion cross sections substantially. This result well follows the systematic behavior of no remarkable role of positive Q-value 2n-stripping channel in sub-barrier fusion of the $ ^{18} {\rm{O}}$-induced systems like $ ^{18} {\rm{O}}$ + $ ^A {\rm{Sn}}$ [41], $ ^{92} {\rm{Mo}}$ [42], $ ^{74} {\rm{Ge}}$ [43]. This conclusion is consistent with the argument that the neutron transfer enhances the sub-barrier fusion cross section only in the case of the increased deformation of the intermediate transfer-channel residual nuclei than that of the initial reactants based on the quantum diffusion approach [38]. This argument was obtained based essentially on a sequential fusion picture of two-step reaction processes like the models used in Refs. [22, 37]. While, this model alone can't explain the no sizeable enhancement for $ ^{36} {\rm{S}}$ + $ ^{58} {\rm{Ni}}$ assisted by positive Q-value 2n-stripping [61], which has an increased deformation after 2n transfer, that is $ ^{36} {\rm{S}}$($ \beta_2 $ = 0.168) + $ ^{58} {\rm{Ni}}$($ \beta_2 $ = 0.183) $ \rightarrow $ $ ^{34} {\rm{S}}$($ \beta_2 $ = 0.257) + $ ^{60} {\rm{Ni}}$($ \beta_2 $ = 0.207) [54]. This suggests other mechanisms should play a role in sub-barrier fusion of heavy-ions.

From the viewpoint of the coupled-channels [30], this consistent systematics reminds us of re-evaluating the potential role of coupling to the proton-stripping channel [62] with effective ground-state Q-value in enhancing sub-barrier fusion, considering the bigger measured 2p-stripping cross sections such as for $ ^{32} {\rm{S}}$ + $ ^{64} {\rm{Ni}}$ even at the low energy very near the barrier [62]. This potential proton-stripping effect was once proposed such as in the pioneering explanation for the isotopic effect in sub-barrier fusion of $ ^{58} {\rm{Ni}}$ + $ ^{64} {\rm{Ni}}$ [22], later $ ^{32} {\rm{S}}$ + $ ^{64} {\rm{Ni}}$ [62] and recent work for $ ^{40} {\rm{Ca}}$ + $ ^{96} {\rm{Zr}}$ [30]. The present result further highlights the complicated mechanisms of sub-barrier heavy-ion fusion, which still needs further studies both experimentally and theoretically.

In summary, we have measured the fusion excitation functions of $ ^{16,18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ at energies near the Coulomb barrier to study the fusion dynamics. Compared to the CC calculated result, the sub-barrier fusion of $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ shows no remarkable 2n-stripping coupling effect. The RE analysis for $ ^{18} {\rm{O}}$ + $ ^{50} {\rm{Cr}}$ gives a quantitative result for this insignificant 2n-stripping effect below the barrier despite the big $ Q^{\mathrm{gs}}_{-2\mathrm{n}} $-value and $ Q^{\mathrm{gs}}_{-2\mathrm{n}} $/$ V_{\mathrm{B}} $-value, compared to few-order enhancement found in some systems with positive Q-value neutron pickup channels below the barrier. Combining with the previous data of $ ^{18} {\rm{O}}$ + $ ^A {\rm{Sn}}$, $ ^{92} {\rm{Mo}}$, $ ^{74} {\rm{Ge}}$, a systematic behavior of no fusion enhancement due to positive Q-value 2n-stripping, across a wide atomic number of the target nuclei, big $ Q^{\mathrm{gs}}_{-2\mathrm{n}} $-value up to +9.11 MeV, and big $ Q^{\mathrm{gs}}_{-2\mathrm{n}} $/$ V_{\mathrm{B}} $-value up to 1/3, has been established. More studies are needed to further confirm this conclusion.

This systematic conclusion could further refresh the popular argument of the sub-barrier fusion enhancement due to positive Q-value 2n transfer during the last decades, and will help to improve the models for clarifying the complicated sub-barrier fusion dynamics in the end. A more sophisticated consideration, such as in a microscopic time-dependent Hartree-Fock theory for consistently describing both the neutron transfer and proton transfer, is needed for a final understanding of the complicated sub-barrier fusion dynamics of heavy-ions.