Search potential for direct slepton pair production at the CEPC with ${ \sqrt{\boldsymbol s}}$ = 360 GeV

Supersymmetry (SUSY) [1-7] postulates the existence of a supersymmetric partner for each Standard Model (SM) particle, with the partner's spin differing by one-half unit. In models that conserve R-parity [8], SUSY particles are produced in pairs. Following a chain of decays, the lightest supersymmetric particle (LSP) remains stable and emerges as a compelling candidate for dark matter [9, 10].

In simplified SUSY models involving only electroweak interactions, the SUSY particle spectrum comprises charginos ($ \tilde\chi^{\pm}_i $, where $ i = 1,2 $ and ordered by increasing mass), neutralinos ($ \tilde\chi^{0}_i $, $ i = 1,2,3,4 $), charged sleptons ($ \tilde{l} $), and sneutrinos ($ \tilde{\nu} $). Charginos and neutralinos are mass eigenstates formed by linear combinations of the superpartners of Higgs bosons and electroweak gauge bosons. Sleptons, the superpartners of charged leptons are categorized as left-handed ($ \tilde{l}_L $) or right-handed ($ \tilde{l}_R $) based on the chirality of their SM counterparts. The mass eigenstates of sleptons, denoted $ \tilde{l}_i $ ($ i = 1,2 $ and ordered by increasing mass), arise from mixing between $ \tilde{l}_L $ and $ \tilde{l}_R $. For the purposes of this paper, we assume mass degeneracy between $ \tilde{l}_L $ and $ \tilde{l}_R $.

Models featuring light staus can produce dark matter relic densities consistent with cosmological observations [11]. Light sleptons also play a role in neutralino co-annihilation processes in the early universe [12, 13]. In both gauge-mediated [14-16] and anomaly-mediated [17, 18] supersymmetry breaking models, slepton masses are typically expected to be on the order of 100 GeV.

Previous searches for direct slepton pair production have been performed at the Large Electron-Positron Collider (LEP) and the Large Hadron Collider (LHC). At LEP, stau (smuon) masses below 96 (99) GeV were excluded for mass splittings between the slepton and the LSP greater than 7 (4) GeV [19-24]. At the LHC, slepton masses up to 700 GeV have been excluded at 95% confidence level for a massless LSP [25, 26]. However, sensitivity diminishes for compressed mass spectra: for instance, slepton masses up to 251 GeV are excluded for a mass splitting of approximately 10 GeV [27]. Using 139 fb⁻¹ of ATLAS data, stau masses up to 500 GeV are excluded at the 95% confidence level [28]; with 77.2 fb⁻¹ of CMS data, masses between 90 and 120 GeV are excluded under the assumption of a nearly massless LSP [29]. For small mass splittings between the slepton and the LSP, sensitivity remains highly limited at hadron colliders—applying both to the LHC [30] and to the projected performance of the High Luminosity LHC (HL-LHC) [31], which is not expected to resolve this limitation. The challenges posed by such compressed regions at the LHC and HL-LHC arise from difficulties in reconstructing low-energy leptons and severe background contamination—limitations that, in turn, highlight the unique advantages of lepton colliders.

The Circular Electron Positron Collider (CEPC) [32] is designed to operate at the key center-of-mass energies: 91.2 GeV as a Z factory for precision Z boson studies, $ \approx $ 160 GeV at the threshold for W boson pair production, and 240 GeV as a Higgs factory for copious Higgs boson production. It can be upgraded to 360 GeV (CEPC-360GeV) —an energy near the $ t\bar{t} $ threshold that enhances sensitivity to Beyond the Standard Model (BSM) physics. A slepton search using CEPC-240GeV with 5.05 ab⁻¹ of integrated luminosity has already been performed: under this configuration, CEPC-240GeV shows potential to discover a combined left- and right-handed stau production up to 116 GeV, or up to 113 GeV for pure $ \tilde{l}_L $ or $ \tilde{l}_R $ scenarios. For smuon production, the discovery potential reaches 117 GeV under the same conditions [33]. This paper presents an analysis of the potential for slepton pair production at CEPC-360GeV with 1.0 ab⁻¹ of integrated luminosity.

Like the CEPC, the International Linear Collider (ILC) and Future Circular Collider for electrons and positrons (FCC-ee) are proposed electron-positron colliders [34, 35]. The CEPC and FCC-ee are circular colliders designed to operate at multiple center-of-mass energies ranging from 90 to 360 GeV, while the ILC is a linear collider with planned energies spanning 250 GeV to 1 TeV. Drawing on prior LEP-based studies [36], a conservative systematic uncertainty of 5% is adopted in this analysis. The results presented in this paper are expected to be largely independent of specific detector, trigger, and data acquisition details, making them applicable as references for the FCC-ee and ILC with appropriate luminosity scaling.

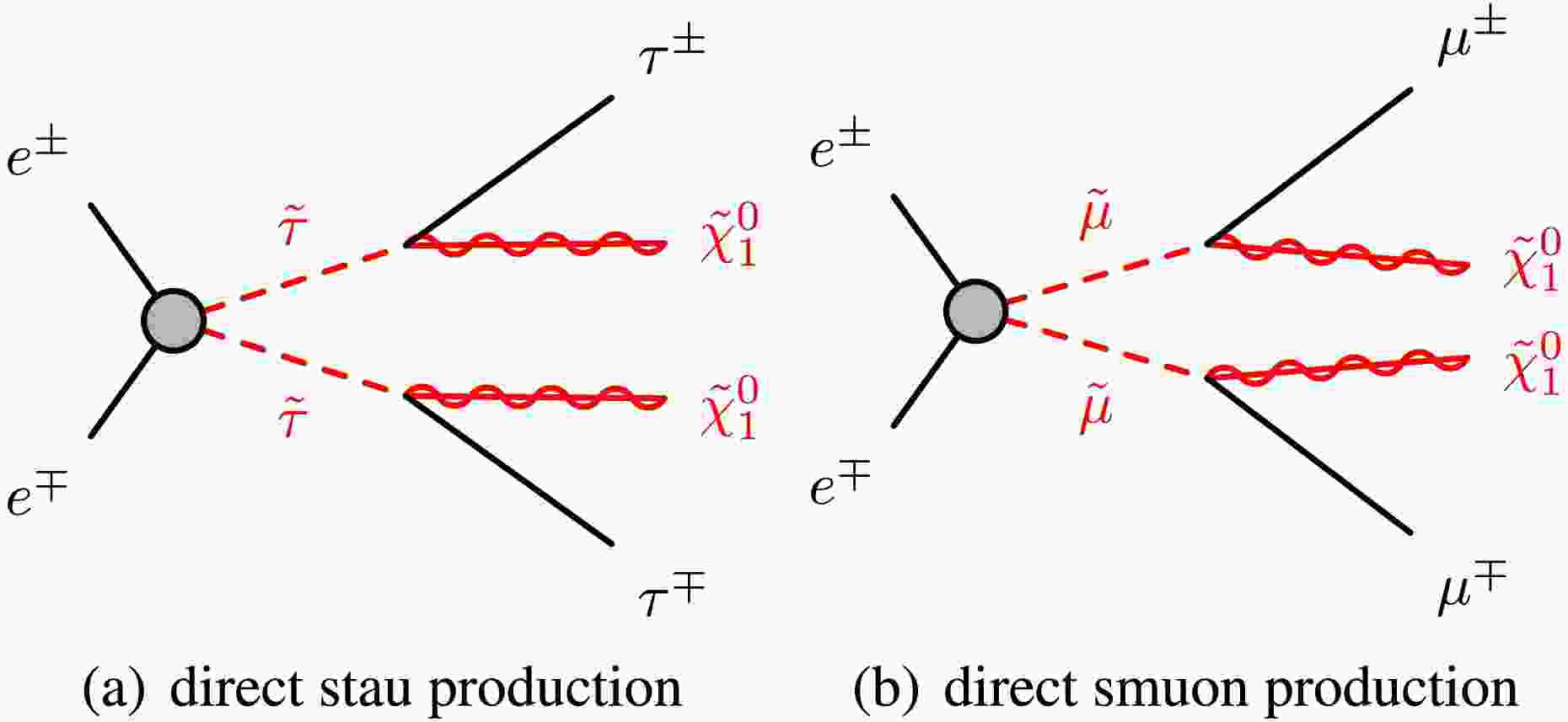
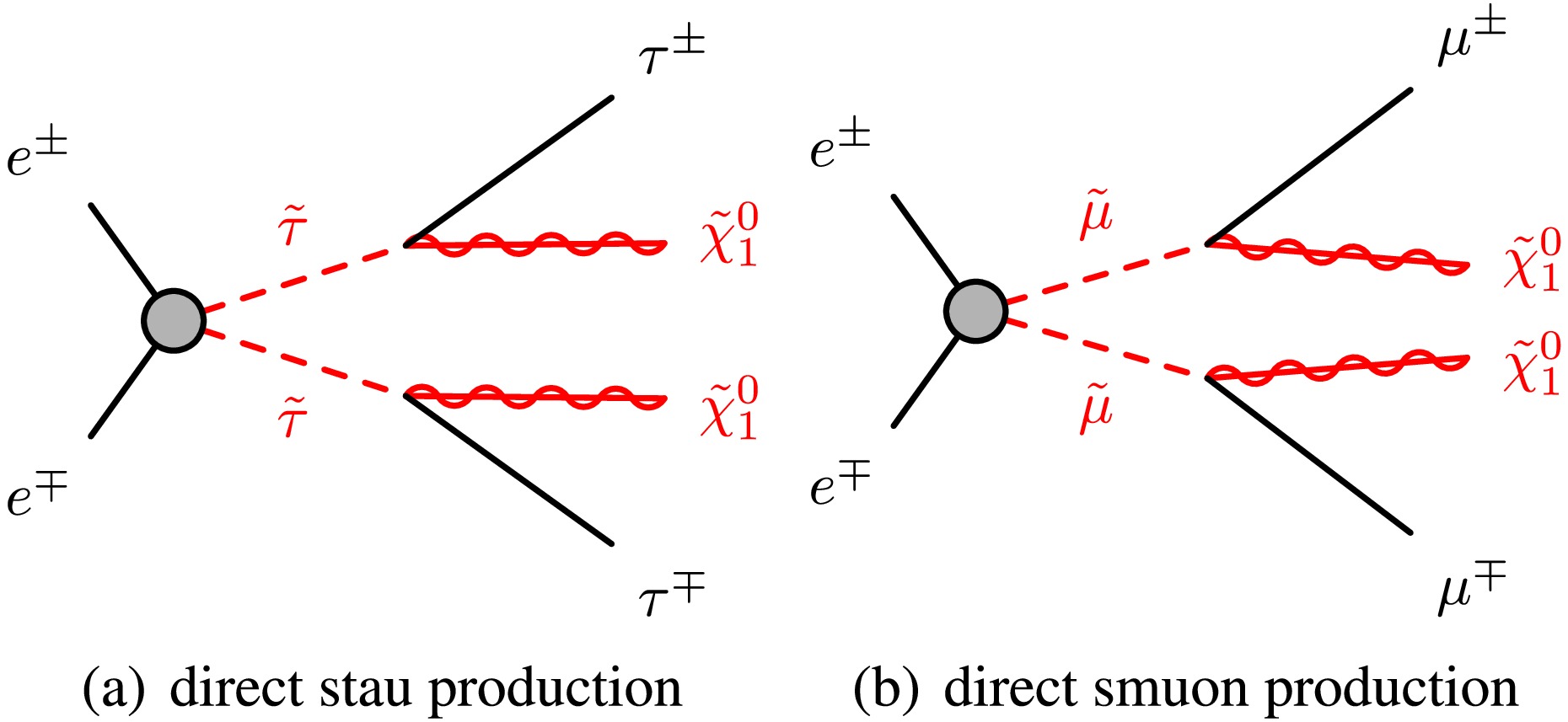
This paper presents sensitivity studies on the direct production of staus and smuons, wherein each slepton is assumed to decay into a lepton (τ or μ) and the lightest neutralino ($ \tilde\chi^0_1 $), as illustrated in Figure 1. In this scenario, the lightest neutralino acts as the LSP and is assumed to be purely Bino in composition.

Figure 1.  (color online) A representative diagram illustrating the pair production of charged staus (smuons) and their subsequent decay into a di-tau (di-muon) final state.

The CEPC Conceptual Design Report (CDR) provides a comprehensive introduction to the detector and associated software [37]. For this Monte Carlo (MC) study, the CEPC baseline detector is employed in full MC simulations, which adhere to the particle flow principle and incorporate an ultra-high-granularity calorimetry system, a low-material silicon tracker, and a 3 Tesla magnetic field. The CEPC baseline tracker comprises a silicon tracking system and a barrel time projection chamber (TPC), resulting in nearly 100% reconstruction efficiencies for muon tracks and tau-decay tracks. Additionally, the momentum resolution of muon tracks reac- hes the per-mille level for momenta ranging from 10 to 100 GeV in the barrel region.

The software employed in the simulation process is as follows: SM background samples were generated using Whi- zard 1.95 [38], with the version consistent with that used in the official CEPC MC production. SUSY signal samples were generated using MadGraph 2.7.3 [39] and Pythia8 [40]. Particle interactions with detector materials were simulated via MokkaC [41]. Track reconstruction was performed using MarlinTraking [42]. The particle flow algorithm, Arbor [32] was utilized to reconstruct all final-state particles. Lepton identification was implemented using LICH [43], which is based on Multivariate Data Analysis via TMVA [44].

In this study, sleptons are pair-produced in electron-posit- ron collisions, with each slepton decaying into a lepton and the lightest neutralino ($ \tilde\chi^0_1 $) with a 100% branching ratio. To simplify the analysis, no other supersymmetric particles are included in the production or decay chains. The mixing matrices for the scalar tau and muon sectors are taken as antidiagonal, precluding mixed production modes. Signal samples for direct stau (smuon) production are parametrized as functions of the masses of $ \tilde{\tau} $ ($ \tilde{\mu} $) and LSP. The $ \tilde{\tau} $ ($ \tilde{\mu} $) mass range is constrained between the LEP limits [19-24] and the CEPC beam energy, spanning 80–179 GeV. Here, left- and right-handed slepton superpartners are assumed to be mass-degenerate. Reference points with $ \tilde{\tau} $ ($ \tilde{\mu} $) masses of 160 (170) GeV and $ \tilde\chi^0_1 $ masses of 50,110,150 (30,120,160) GeV are used to illustrate key analysis features. Theoretical cross sections for slepton pair production at CEPC- 360GeV are calculated at leading order (LO) using $ \mathrm{MadGraph}$ [39], yielding 42.22 fb for $ \tilde{\tau} $ (160 GeV) and 22.34 fb for $ \tilde{\mu} $ (170 GeV).

In this analysis, Standard Model (SM) background processes include both fully decaying $ t\bar{t} $ events and non-$ t\bar{t} $ processes featuring two leptons (taus, muons, or electrons) with large recoil mass. The background categories comprise $ t\bar{t} $ production, two-fermion processes, four-fermion processes, and selected Higgs processes. The Higgs background is restricted to the $ \nu\nu H $ channel, encompassing all possible Higgs decay modes. The two-fermion processes consist of $ \mu\mu $ and $ \tau\tau $ final states, while four-fermion processes include $ ZZ $, $ WW $, single-Z, single-W, and mixed Z/W production. The two-photon background arises from processes including ee $ \to $ eeee, ee $ \to $ $ \mu\mu $ee, and ee $ \to $ $ \tau\tau $ee. The labels for four-fermion processes in Table 1 are defined solely by the distinct manner in which the four final-state fermions associate with the underlying Z and W boson combinations. All such processes incorporate the full set of contributions— s-channel, t-channel, and their interference, as required by the Standard Model. Additionally, the processes listed in the table are mutually exclusive, with no overlapping event contributions. The two-photon background were generated using FDC (Feynman Diagram Calculation) [45], where the two t-channel photon exchange diagrams provide the leading-order contribution for the beamstrah- lung effect. Therefore, higher-order contributions from beamstrahlung are omitted here, and a more precise investigation can be performed if needed in the future. All simulated samples are normalized to an integrated luminosity of 1.0 ab⁻¹. The cross sections of the considered background processes are summarized in Table 1.

Event reconstruction consists of three main components: track reconstruction, particle flow reconstruction, and compound physics object reconstruction. Tracks are reconstructed from detector hits using $ \mathrm{Clupatra}$ [42]. Particle flow reconstruction combines track and calorimeter information to reconstruct individual particle-level objects, which are then used to build compound physics objects such as converted photons, taus, and jets. The identification efficiency for light leptons (electrons and muons) exceeds 99.5% for particles with energies above 2 GeV [43]. For electrons and muons with energies below 1 GeV, particularly those in the barrel edge or barrel-endcap transition regions, the identification efficiency is approximately 90%.

The CEPC exhibits distinct properties, including precise energy-momentum conservation (arising from its clean, symmetric initial state), reduced background noise, and a well-defined center-of-mass frame. Variables associated with invariant mass, lepton/photon momentum and energy, angular distributions, and lepton flavor or charge are particularly effective in this context: they capitalize on the collider’s clean initial state and predictable final states to probe new physics with unparalleled precision. Building on this detailed characterization of lepton collider kinematics, the following variables efficiently discriminate signal events from SM backgrounds:

– $ |\varDelta \phi(\ell,recoil)| $, the difference of azimuth between one lepton and the recoil system.

– $ |\varDelta \phi(\ell,\ell)| $, the difference of azimuth between two leptons.

– $ \varDelta R(\ell,recoil) $, the angular distance between one lepton and the recoil system. ¹

– $ \varDelta R(\ell,\ell) $, the angular distance between two leptons.

– $ E_{\ell} $, the energy of one lepton.

– $ P_T $, the sum of the transverse momentum of two leptons.

– $ M_{\ell\ell} $, the invariant mass of two leptons.

– $ M_{recoil} $, the recoil mass of the di-lepton pair, as defined in Equation (1), where l denotes a muon (tau) track originating from smuon (stau) pair production.

To mitigate the impact of potential correlations between variables, the optimization of signal regions relies on an N-dimensional scan over the aforementioned kinematic variables, achieved by applying varying cut values. The cut combination yielding the highest signal sensitivity is selected and further validated by reassessing kinematic distributions within the relevant regions. Ultimately, signal regions are defined using the final selected kinematic criteria. To estimate the sensitivity to the signal, the median significance is employed, as it offers a more accurate approximation of the true significance in regions where the number of signal events is non-negligible. This significance, denoted as $ Z_\mathrm{n} $, is calculated using the method described in Ref. [46], as shown in Equation (2).

In the calculation of Zn, both statistical uncertainty and 5% flat systematic uncertainty are incorporated. This approach is widely adopted in optimization studies for new physics searches across experiments such as ATLAS.

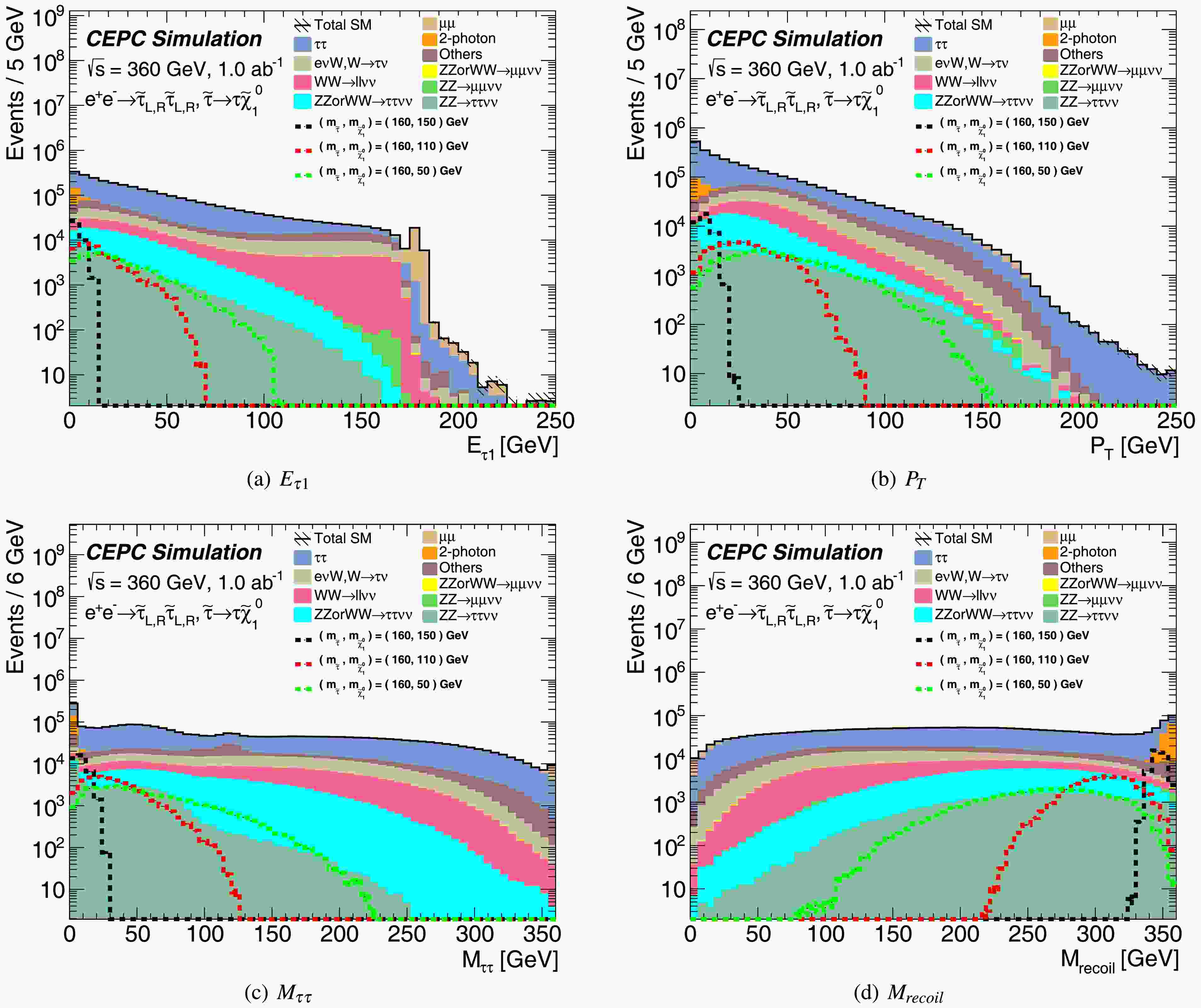
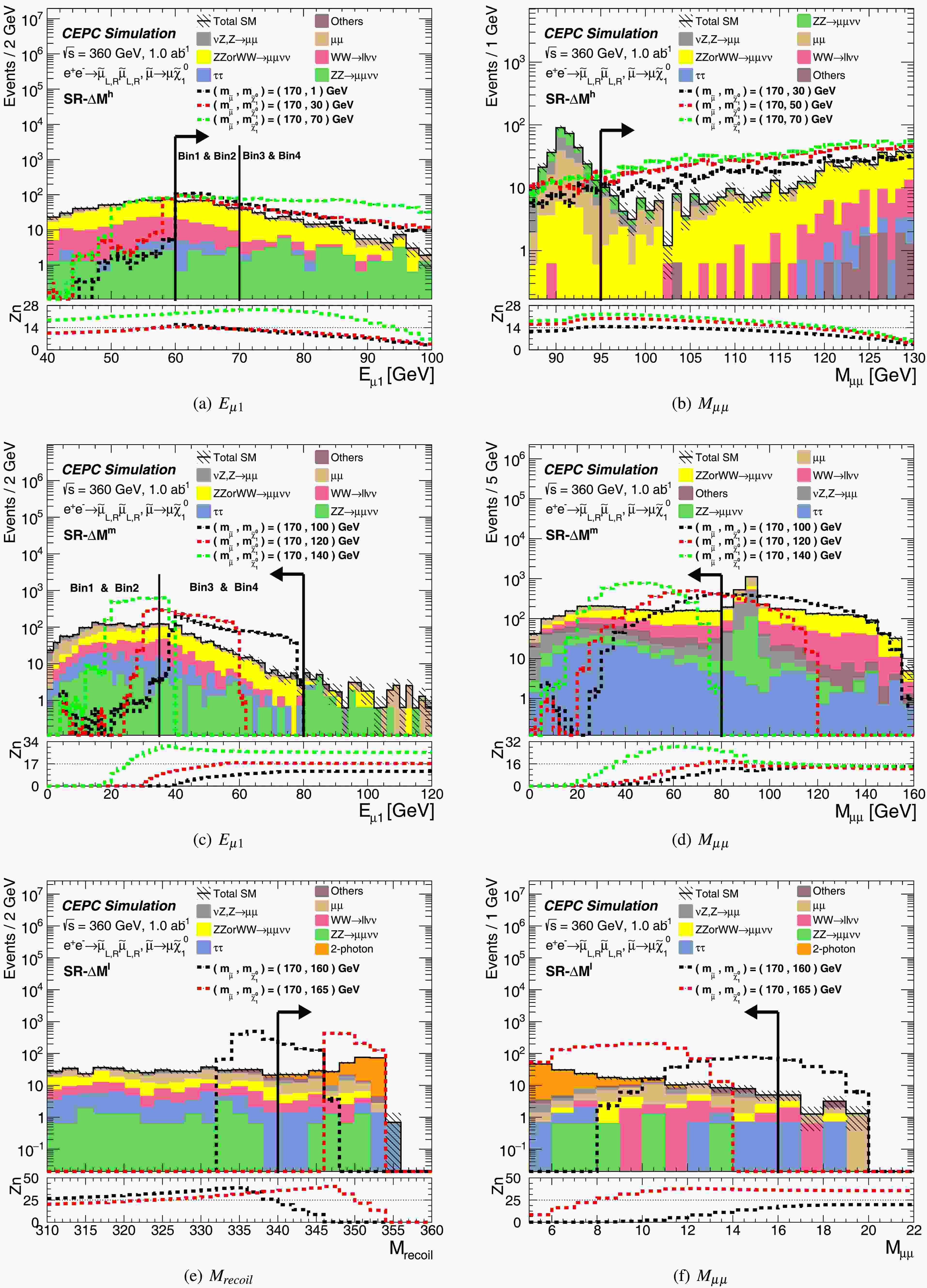
For the preselection in the search for direct stau production, the following criteria are applied: the two most energetic tracks are required to have exactly opposite charges, with each satisfying an energy threshold exceeding 2.5 GeV and an absolute pseudorapidity less than 2.5—this criterion is implemented to suppress the two-photon background. Additionally, at least one of these two tracks must originate from a hadronic tau decay. The negatively charged track is then identified as a tau lepton, while the positively charged track is identified as an anti-tau lepton. Key kinematic distributions after preselection are presented in Figure 2, demonstrating strong discrimination power between signal events and Standard Model background processes.

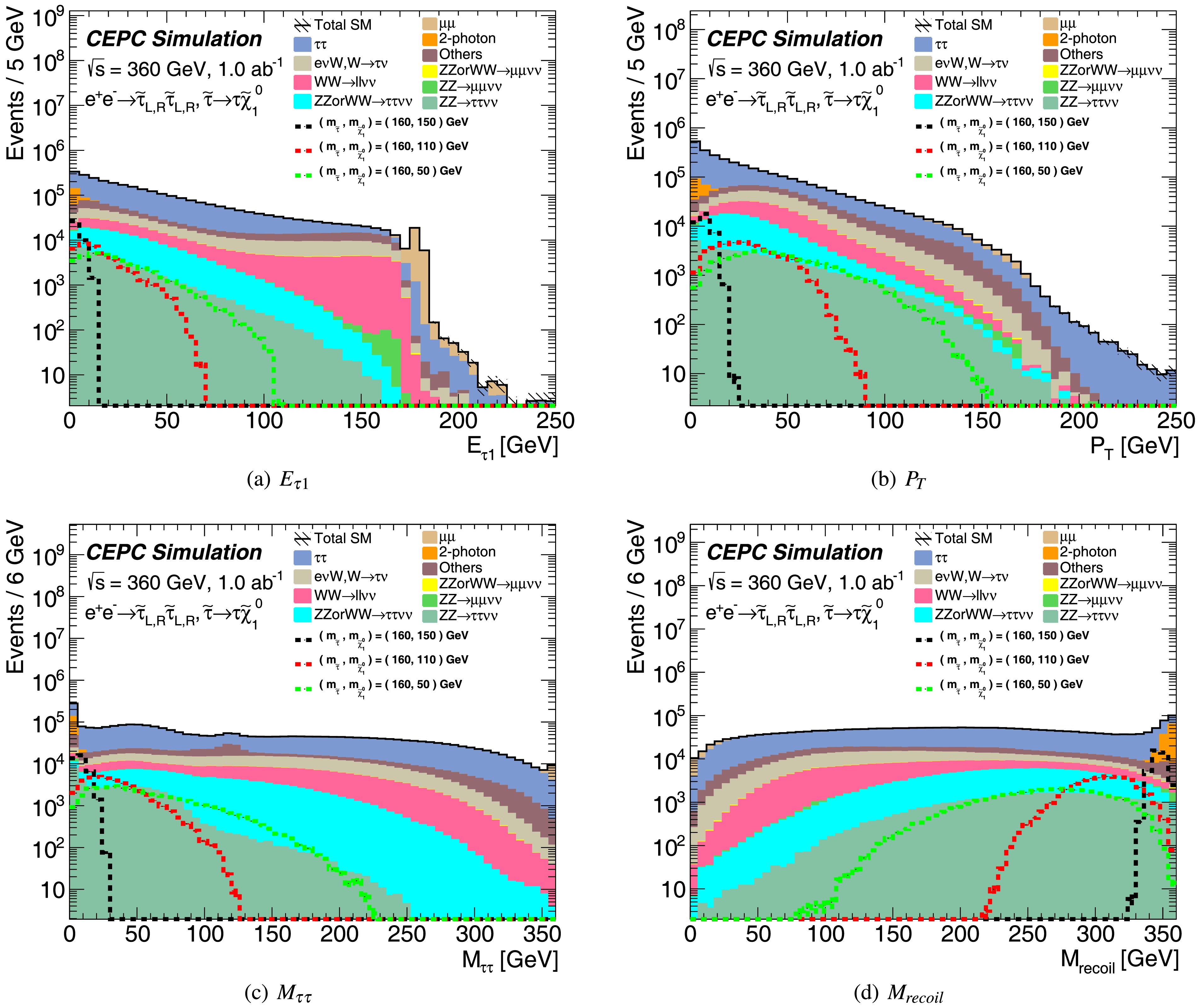
Figure 2.  (color online) The kinematic distributions for direct stau pair production after the two OS tau selection with $ E_{\tau} $ larger than 2.5 GeV. The stacked histograms show the expected SM background. To illustrate, the distributions of three SUSY reference points are shown as dashed lines.

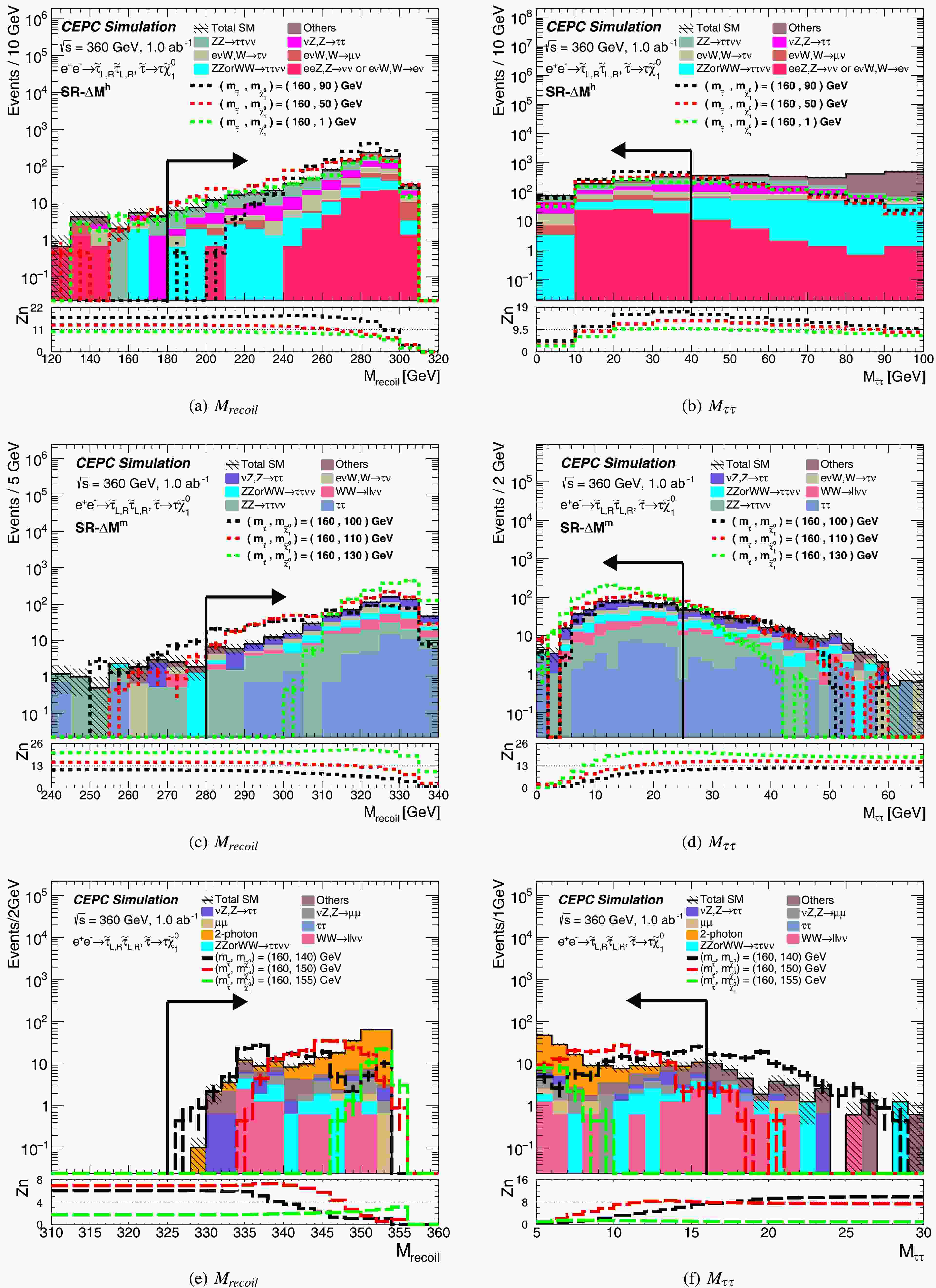
Since signal behaviors depend on the mass splitting between $ \tilde{\tau}$ and $ \tilde\chi^0_1$ ($ \varDelta M $), as shown in Figure 2, three signal regions (SRs) are designed to cover the whole $ \tilde{\tau}$-$ \tilde\chi^0_1$ mass parameter space. SR-$ \varDelta M^h $ encompasses the high-$ \varDelta M $ region, SR-$ \varDelta M^m $ covers the medium-$ \varDelta M $ region, and SR-$ \varDelta M^l $ spans the low-$ \varDelta M $ region. The definitions of these signal regions are summarized in Table 2. An upper cut on the tau energy ($ E_{\tau} $) is applied to suppress $ \mu\mu $, Z or W mixing, WW, eνW and eeZ processes. A lower cut on the sum of the transverse momentum of two leptons ($ P_{T} $) is implemented to reduce backgrounds from $ \tau\tau $, $ \mu\mu $ and νZ processes. Given the signal topology, most signal events exhibit a large recoil mass; Thus, a lower cut on the invariant mass of the recoil system ($ M_{recoil} $) is used to reject $ \tau\tau $, eνW processes, and other SM processes lacking significant recoil mass. Upper cuts on the $ \tau\tau $ invariant mass ($ M_{\tau\tau} $) further suppress $ \tau\tau $ and eνW backgrounds, while a lower cut on $ M_{\tau\tau} $ in the SR-$ \varDelta M^l $ region is primarily implemented to reduce the two-photon background. Additional suppression of $ \tau\tau $ and $ \mu\mu $ processes is achieved via selections on $ |\varDelta \phi(\tau,\tau)| $ and $ |\varDelta \phi(\tau,recoil)| $. Selections on $ \varDelta R(\tau,\tau) $ are employed to further reject $ \tau\tau $, ZZ and single-Z processes. The same signal regions are used for both left-handed and right-handed staus, as their kinematic behaviors are nearly identical, with only small differences in production cross sections.

The kinematic distributions of $ M_{recoil} $ and $ M_{\tau\tau} $, after applying signal region requirements, except those on the variable to be shown are presented in Figure 3. The lower panel of each plot displays the expected sensitivity Zn as a function of $ M_{recoil} $ and $ M_{\tau\tau} $, respectively, demonstrating that the requirements on these variables effectively distinguish signal events from the Standard Model backgrounds. Table 3 summarizes the event yields from background processes and reference signal points after applying the full signal region criteria. The dominant background contributions originate from $ ZZ \to \tau\tau\nu\nu $, $ \nu Z , Z \to \tau\tau $, $ ZZ $ or $ WW \to \tau\tau\nu\nu $, $ ZZ \to \mu\mu\nu\nu $, $ WW \to \ell\ell\nu\nu $, $ \nu Z , Z \to \mu\mu $, $ \tau\tau $ and $ \mu\mu $ processes.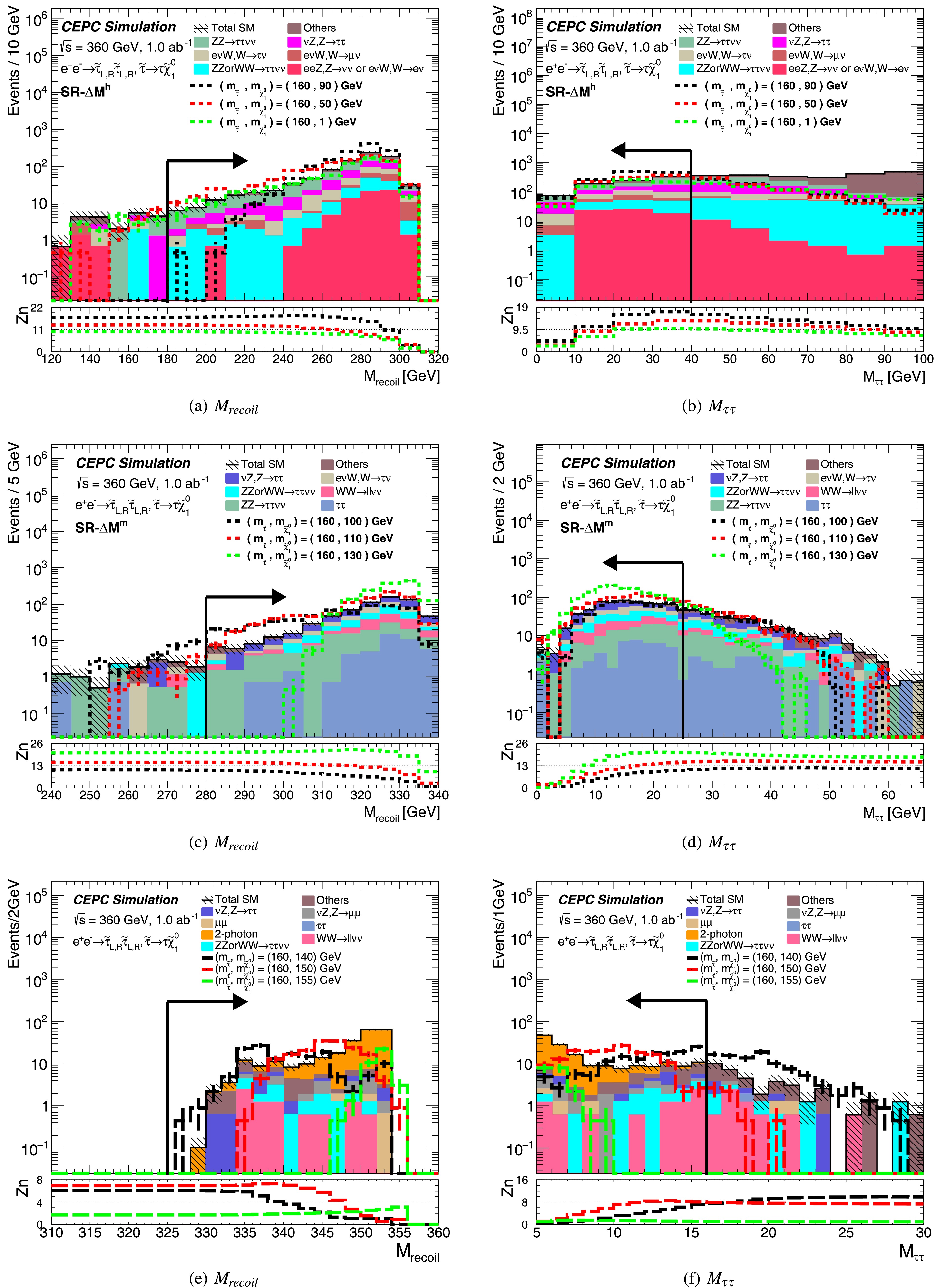

Figure 3.  "N-1" distributions after signal region requirements for the direct stau pair production. All signal region requirements are applied except for the variable shown. The stacked histograms show the expected SM backgrounds. To illustrate, the distributions from SUSY reference points are shown as dashed lines. The lower pad is the sensitivity Zn calculated with a statistical uncertainty and a 5% flat systematic uncertainty.

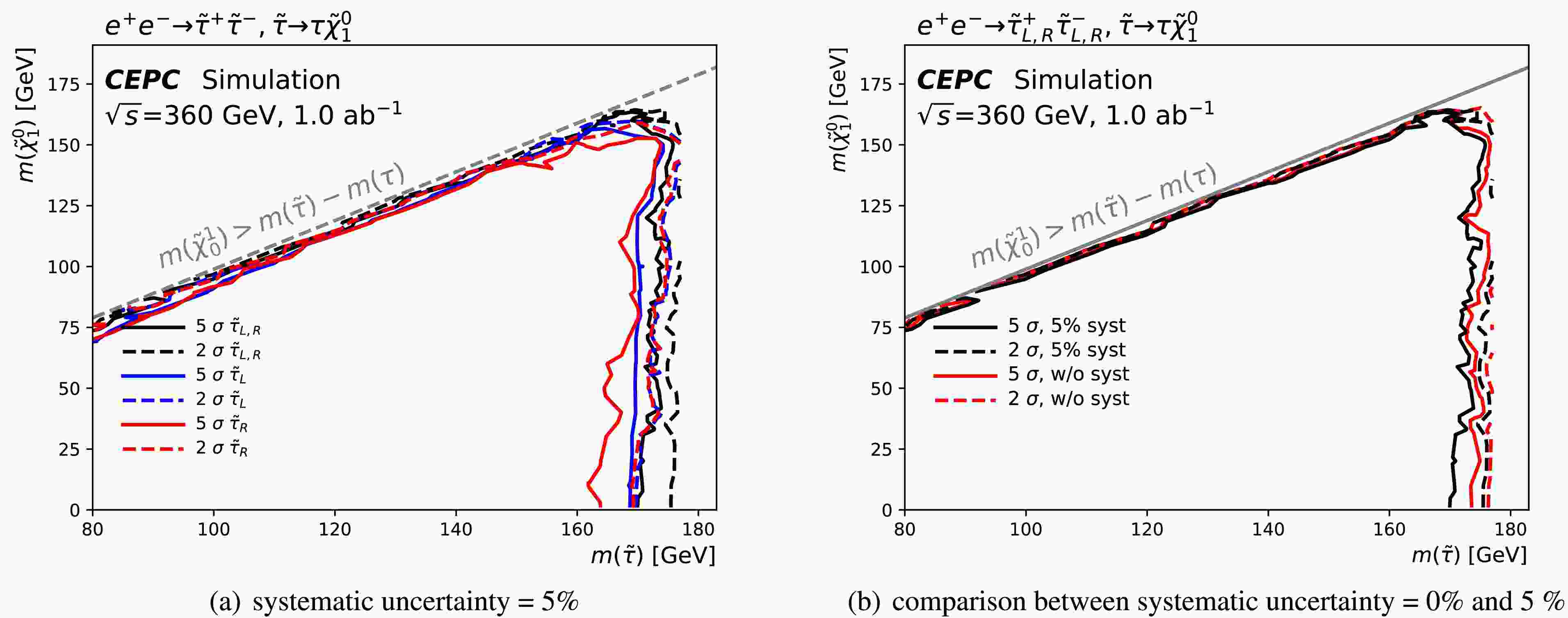
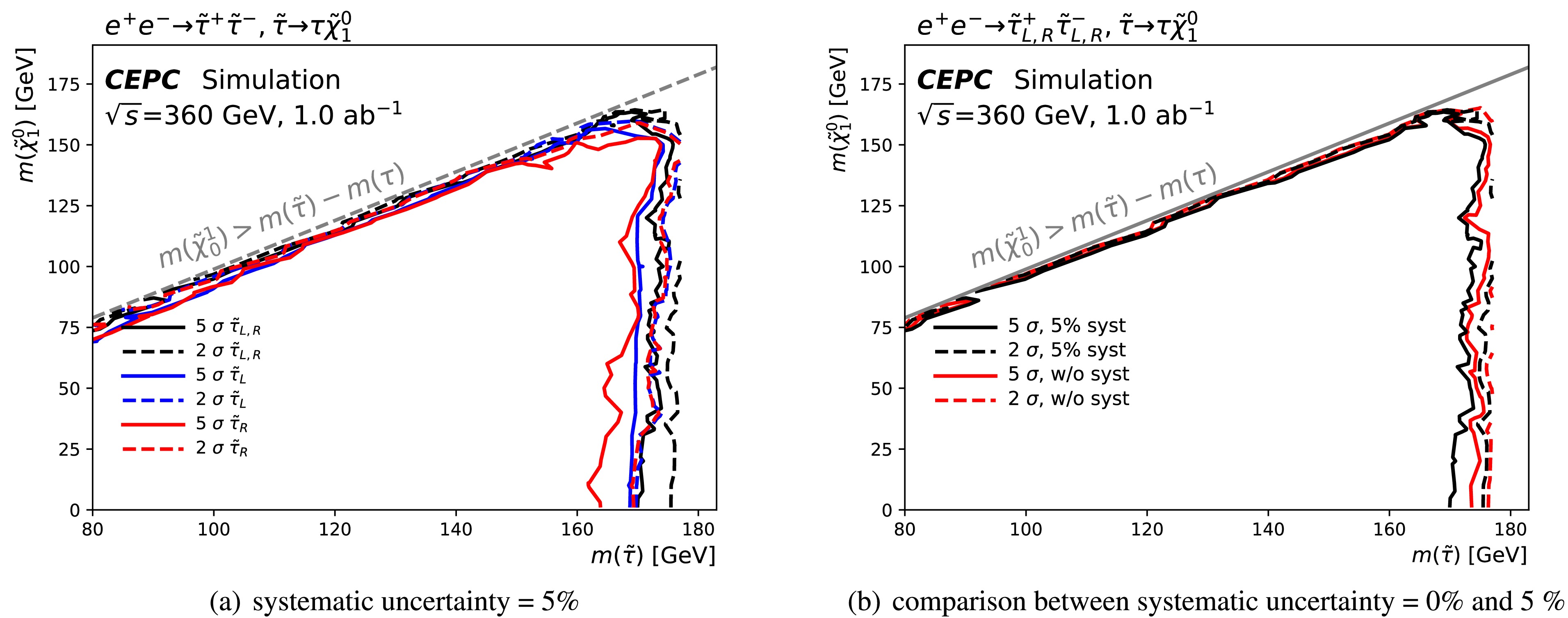
Figure 4 presents the projected exclusion ($ 2\sigma $) and discovery ($ 5\sigma $) contours for direct $ \tilde{\tau} $ production, under the assumption of 0% systematic uncertainties (no systematics) and 5% systematic uncertainties. The sensitivity of each signal point is derived using the optimum expected limits from SR-$ \varDelta M^h $, SR-$ \varDelta M^m $, and SR-$ \varDelta M^l $. To assess the impact of detector-related systematics, a conservative 5% flat systematic uncertainty—consistent with the LEP experiment—is adopted. Under this framework, the discovery reach extends up to 170 GeV for the combined left- and right-handed stau scenario, and up to 169 GeV and 162 GeV for purely left-handed and right-handed staus, respectively. These results indicate only limited degradation of sensitivity due to the detector systematics. Since the most sensitive signal region is selected for each individual point, adjacent signal points in overlapping regions may be associated with different signal regions, which can result in non-smooth contours. The resulting limits extend the LEP exclusion bounds by approximately 74 GeV and bridge the gap in the exclusion reach of LHC experiments within the compressed region, as reported in Ref. [30].

Figure 4.  (color online) The projected exclusion (2σ) and discovery ($ 5\sigma $) contours for direct $ \tilde{\tau} $ production at the CEPC.

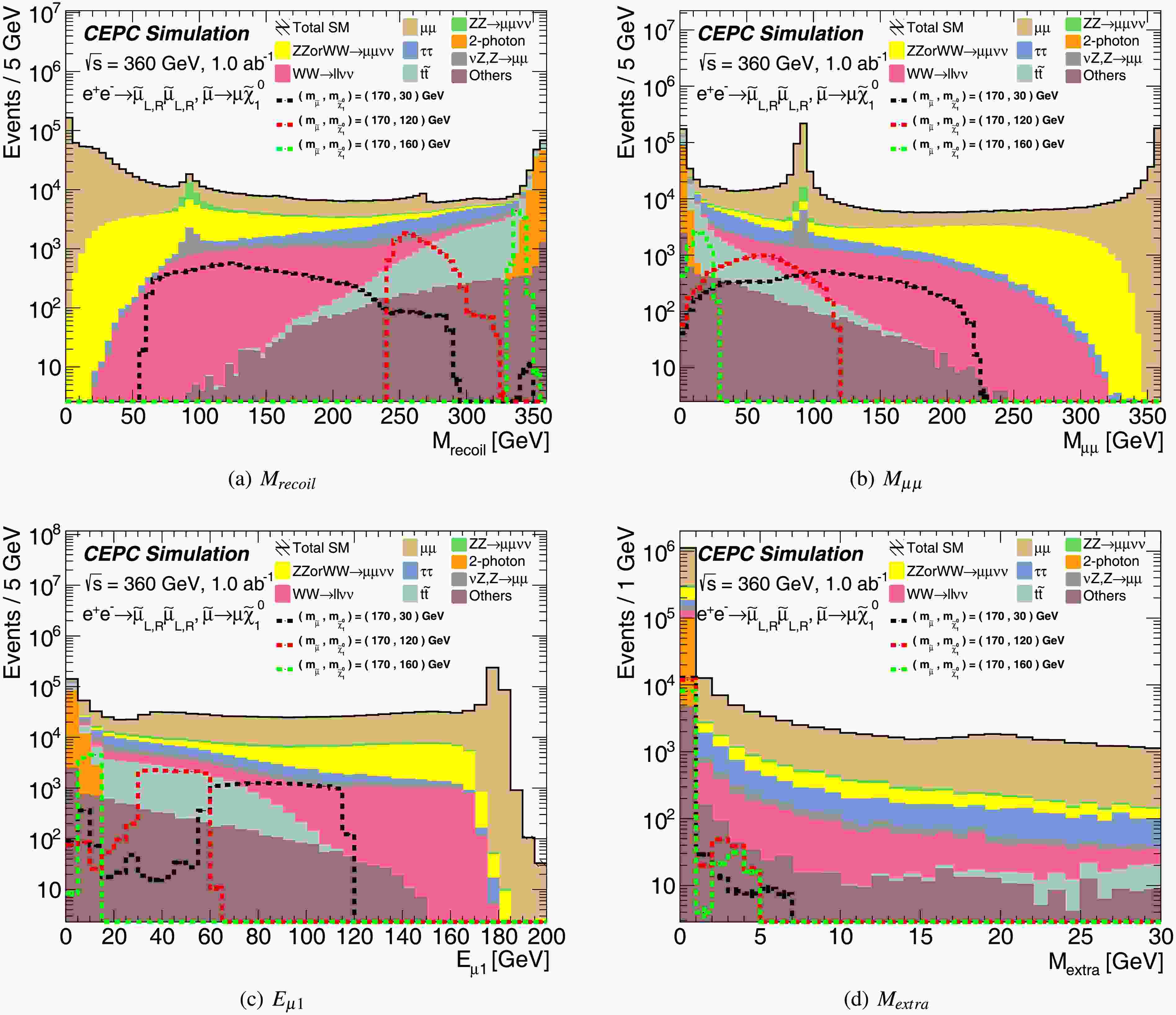
For smuon pair production, events are selected that contain exactly two OS muons, each satisfying an energy threshold exceeding 2.5 GeV and an absolute pseudorapidity less than 2.5. This criterion is implemented to suppress the two-photon background. The kinematic distributions of the variables used in the analysis, after applying the above selection criteria, are presented in Figure 5, demonstrating strong discrimination power between signal events and the Standard Model background processes.

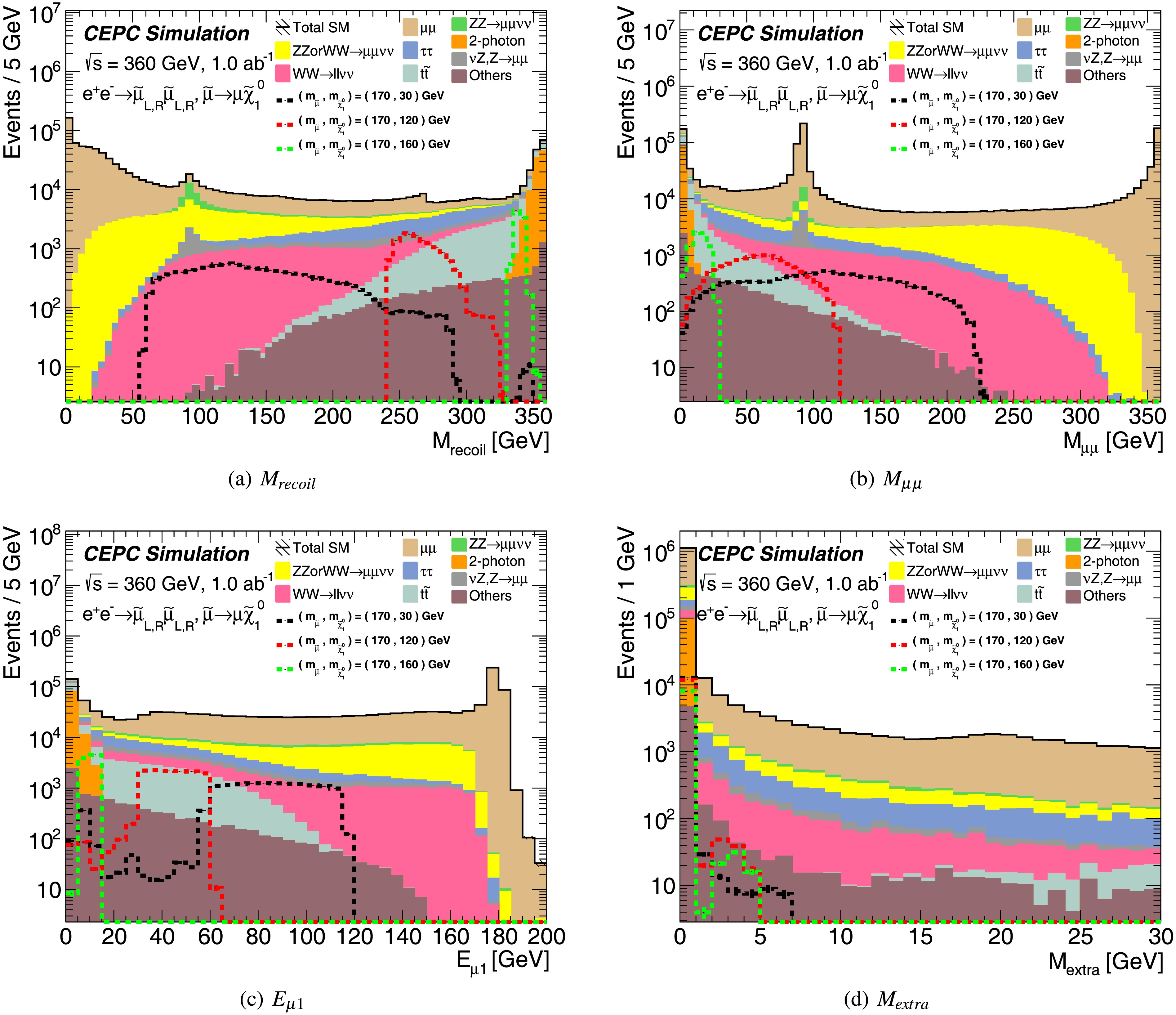
Figure 5.  (color online) The kinematic distributions for direct smuon pair production after applying the preselection. The stacked histograms show the expected SM background. To illustrate, the distributions of three SUSY reference points are shown as dashed lines.

Similar to stau pair production, three SRs are designed to cover different mass splittings between $ \tilde{\mu}$ and $ \tilde\chi^0_1$ ($\varDelta M$). The SR- $\varDelta M^h$ encompasses the high- $\varDelta M$ region, SR- $\varDelta M^m$ covers the medium- $\varDelta M$ region, and SR- $\varDelta M^l$ spans the low- $\varDelta M$ region. To enhance signal sensitivity, the SR- $\varDelta M^h$ and SR- $\varDelta M^m$ regions are further subdivided into intervals based on the energies of the leading and sub-leading muons (${\rm{E }}_{\mu1}$ and ${\rm{E }}_{\mu2}$, collectively denoted as ${\rm{E }}_{\mu1,2}$), where $\mu1$ ($\mu2$) refers to the muon with the highest (second-highest) energy. The definitions of signal regions are summarized in Table 4 Selections on ${\rm{E }}_{\mu1,2}$ are applied to reject $\tau\tau$ and νZ background processes. Cuts on $\varDelta R(\mu, recoil)$ are used to suppress $\tau\tau$, $\mu\mu$ and ZZ backgrounds, while cuts on the dimuon invariant mass $M_{\mu\mu}$ target the suppression of WW, $\mu\mu$, two-photon and other Z-related backgrounds. Consistent with the signal topology, where most signal events exhibit a large recoil mass, a lower cut on the invariant mass of the recoil system ($M_{recoil}$) is implemented to reject $\mu\mu$, Z or W mixing processes, and other Standard Model processes lacking significant recoil mass. Additionally, the invariant mass of all extra reconstructed visible particles (with energies above 0.5 GeV, excluding the two oppositely charged muon tracks), denoted as $M_{extra}$, is utilized to strongly suppress $t\bar{t}$ background.

The kinematic distributions of $M_{recoil}$, $M_{\mu\mu}$, $E_{\mu1}$ and $\varDelta R$ $(\mu,recoil)$ —after applying all signal region requirements except those on the variable being displayed are presented in Figure 6. The lower panel of each plot shows the expected sensitivity Zn as a function of $M_{recoil}$, $M_{\mu\mu}$, $E_{\mu1}$ and $\varDelta R$ $(\mu,recoil)$, respectively, demonstrating that selections on $M_{recoil}$ and $M_{\mu\mu}$ effectively distinguish SUSY signal events from Standard Model background processes. Table 5 summarizes the event yields from all background processes and reference signal points after applying the full signal region criteria. The dominant background contributions originate from $ZZ$ or $WW \to \mu\mu\nu\nu$, $\mu\mu$, $WW\to\ell\ell\nu\nu$, $ZZ\to\mu\mu\nu\nu$, $\tau\tau$, $ZZ$ or $WW \to \tau\tau\nu\nu$ and $\nu Z (Z\to\tau\tau$) processes.

Figure 6.  (color online) "N-1" distributions after signal region requirements for the direct smuon pair production. All signal region requirements are applied except for the variable shown. The stacked histograms show the expected SM backgrounds. To illustrate, the distributions from SUSY reference points are shown as dashed lines. The lower pad is the sensitivity Zn calculated with a statistical uncertainty and a 5% flat systematic uncertainty.

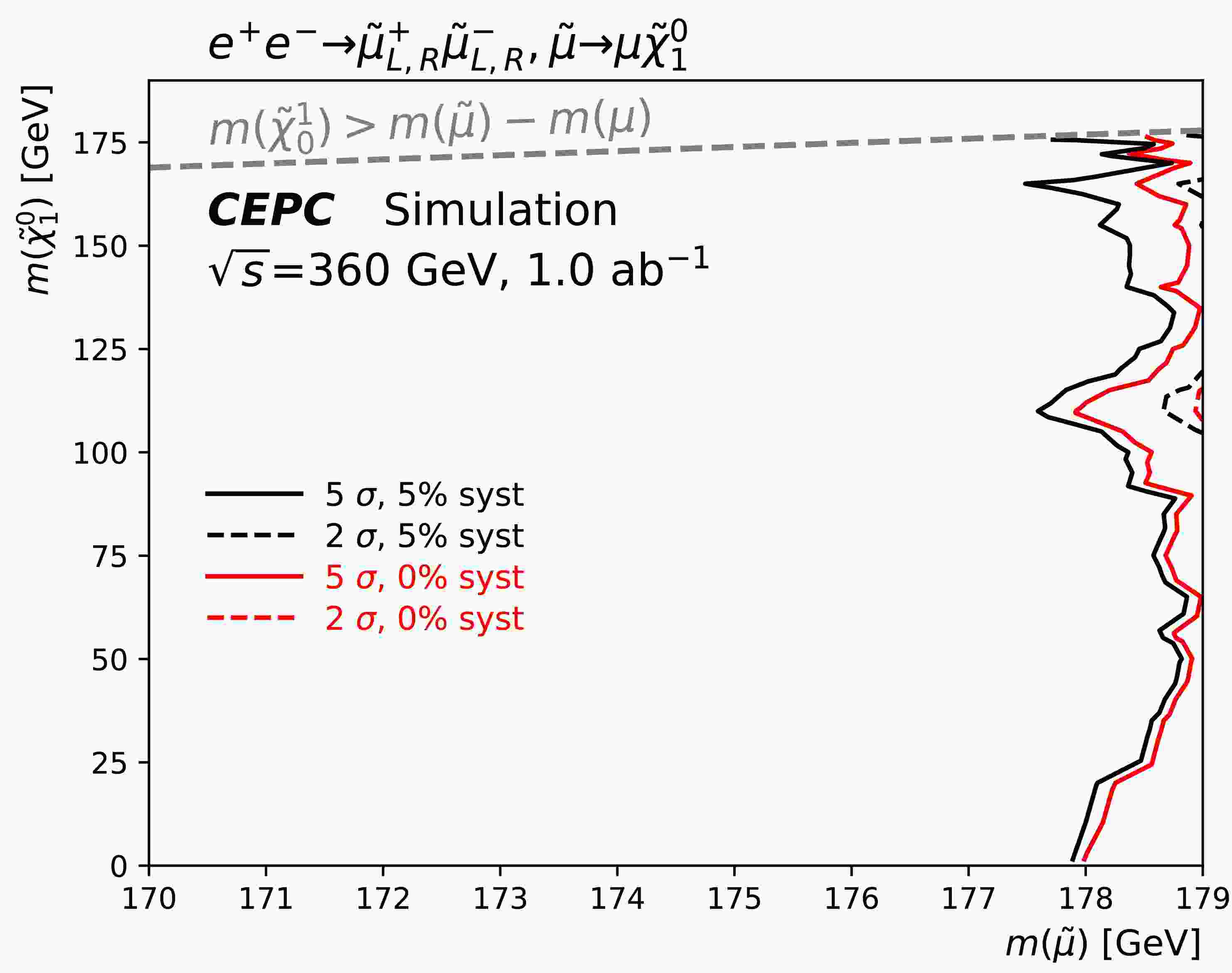
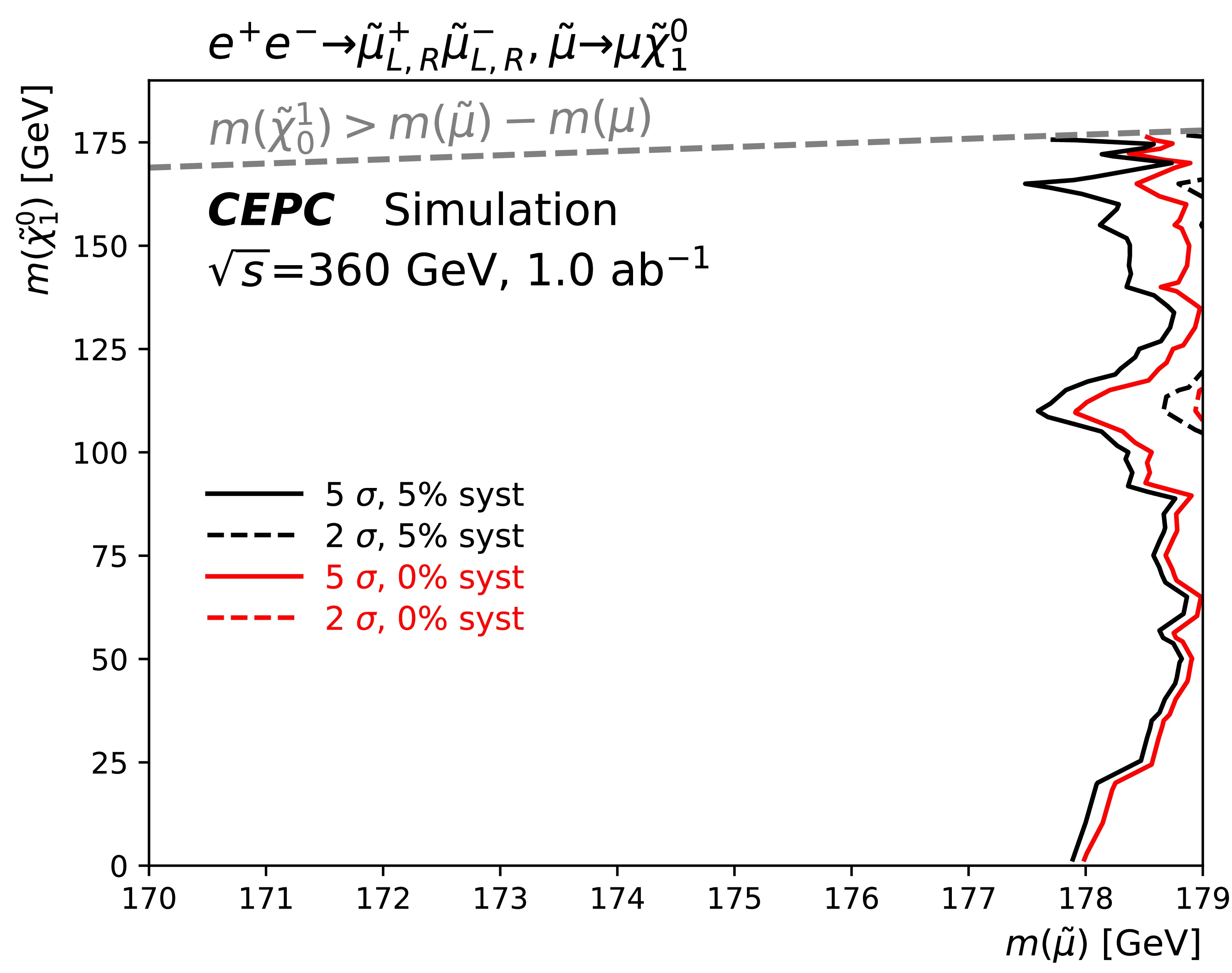
Figure 7 shows the projected exclusion ($2\sigma$) and discovery ($5\sigma$) contours for direct smuon production, assuming 0% and 5% systematic uncertainties. The sensitivity at each signal point is derived using the optimal expected limits from SR- $\varDelta M^h$, SR- $\varDelta M^m$, and SR- $\varDelta M^l$. Under the assumption of a 5% flat systematic uncertainty, the discovery reach extends up to 178 GeV in $\tilde{\mu}$ mass, with minimal degradation attributed to detector-related systematics. Since the most sensitive signal region is selected for each individual point, adjacent signal points in overlapping regions may be associated with different signal regions, potentially resulting in non-smooth contours. This result extends the LEP exclusion limits by approximately 79 GeV and bridges the gap in the compressed mass region left by LHC experiments, as documented in Ref. [30].

Figure 7.  (color online) The projected exclusion ($2\sigma$) and discovery ($5\sigma$) contours for direct $ \tilde{\mu}$ production at the CEPC, under the assumptions of 0% and 5% systematic uncertainties.

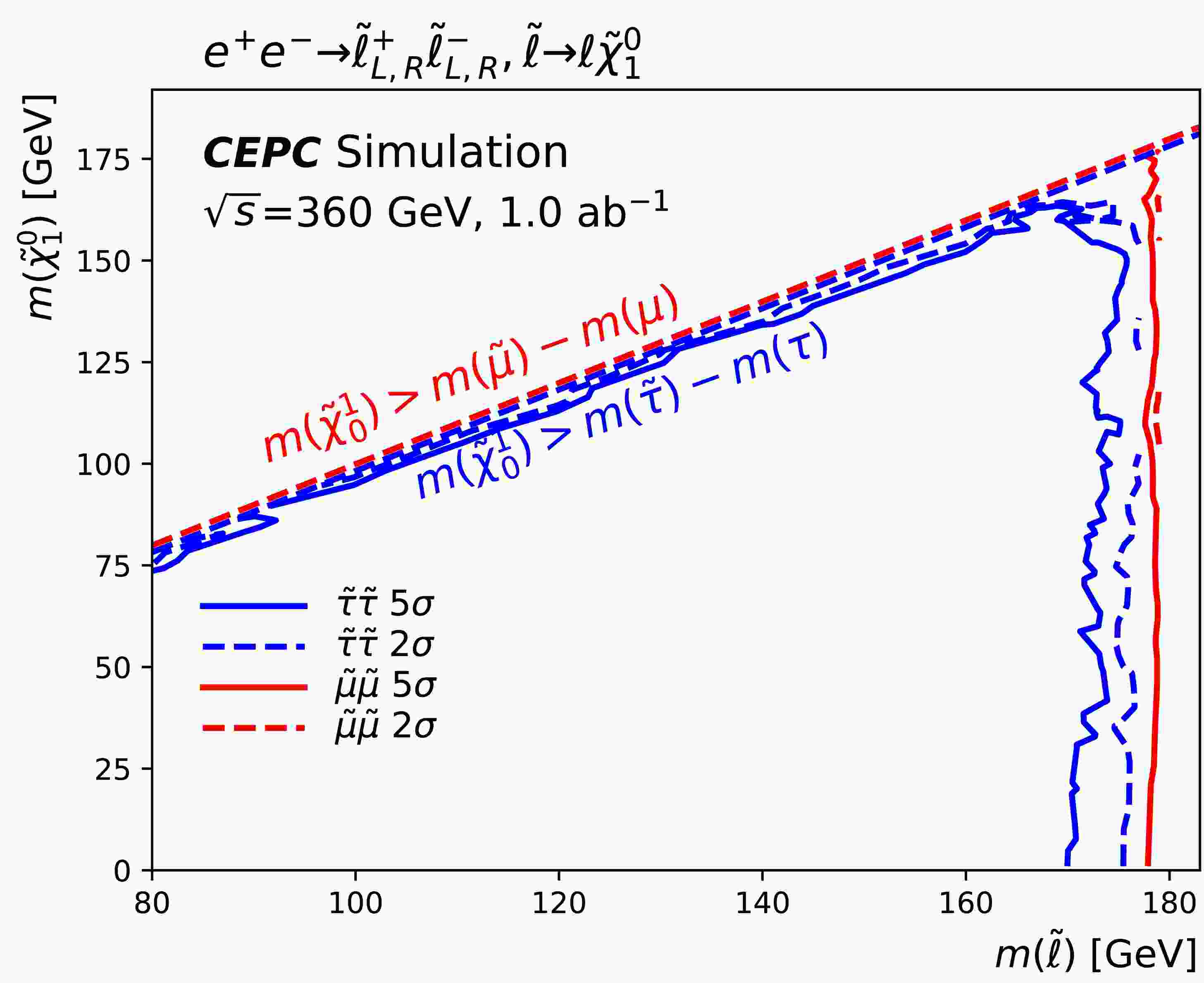
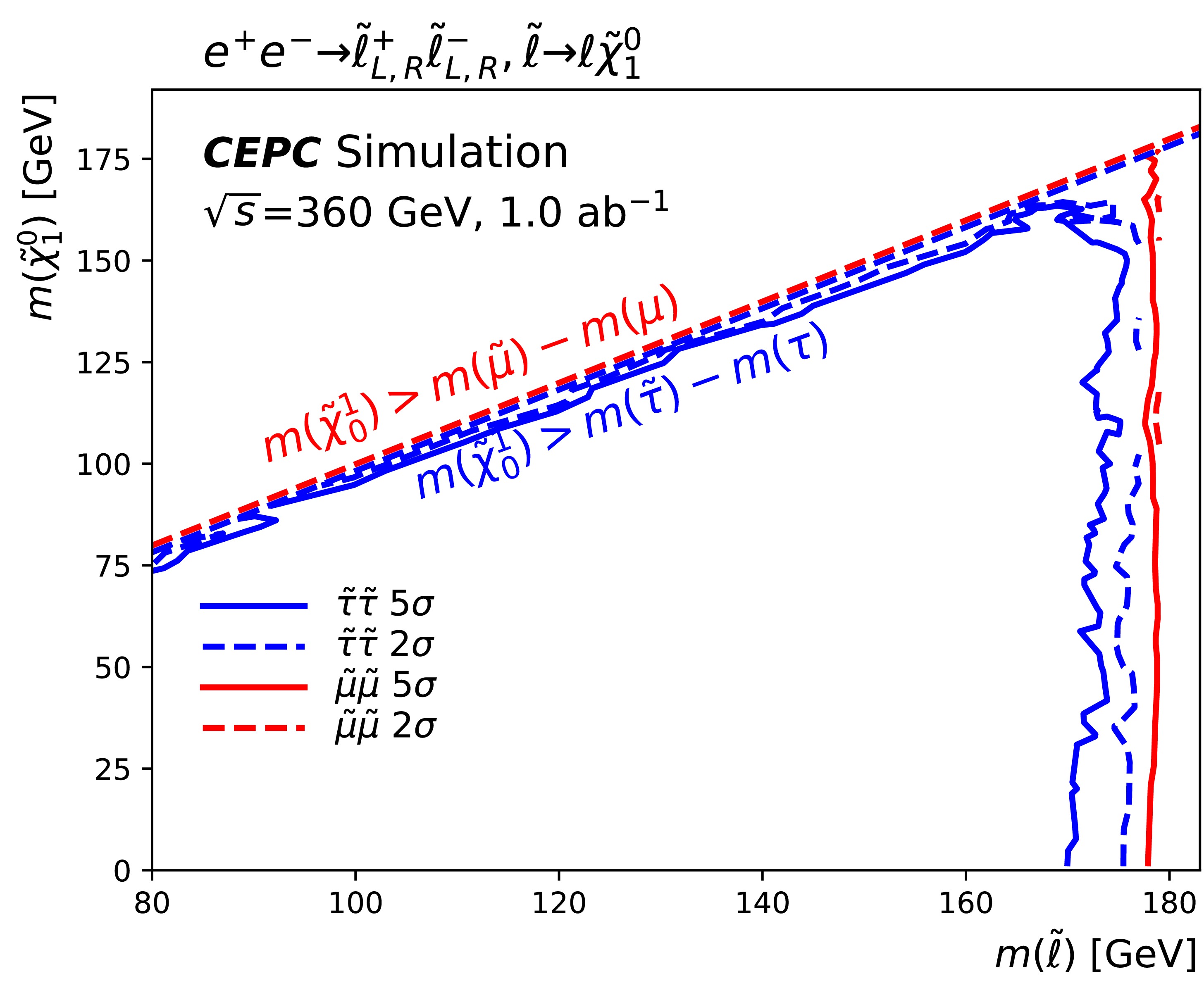
Figure 8 presents the projected exclusion and discovery contours at the CEPC for direct $\tilde{\tau}$ and $\tilde{\mu}$ production, assuming a 5% flat systematic uncertainty. For direct stau production, the discovery reach extends up to 170 GeV in stau mass for the combined left- and right-handed scenario, with respective reaches of 169 GeV and 162 GeV for purely left-handed and right-handed staus. For direct smuon production, the discovery potential reaches up to 178 GeV in smuon mass. Given the similar design and performance characteristics of future $e^+e^-$ collider facilities, these results serve as a valuable reference for other proposed experiments with comparable center-of-mass energies and target luminosities, such as the ILC [34] and FCC-ee [35].

Figure 8.  (color online) The projected exclusion ($2\sigma$) and discovery ($5\sigma$) contours for direct $ \tilde{\tau}$ and direct $ \tilde{\mu}$ production at the CEPC, under the assumptions of 5% systematic uncertainties.

Searches for direct slepton pair production are performed at the CEPC using fully simulated MC samples, assuming a center-of-mass energy of $\sqrt{s} = 360$ GeV and an integrated luminosity of 1.0 ab⁻¹. The mass reach for $\tilde{\tau}$ ($\tilde{\mu}$) extends approximately 74 (79) GeV beyond the previous limits set by LEP in the high-mass region. Furthermore, the analysis exhibits sensitivity to the compressed mass region—where the mass difference between $\tilde{\tau}$ ($\tilde{\mu}$) and the LSP is small—a regime that remains challenging for ATLAS and CMS to probe effectively. This MC study provides compelling motivation for upgrading the CEPC’s center-of-mass energy from 240 GeV to 360 GeV, thereby enhancing its capability to search for sleptons.

The authors are grateful to Manqi Ruan, Chengdong Fu, Gang Li, Xianghu Zhao, Ronggang Ping and Dan Yu for their valuable assistance with CEPC simulations, and to Lorenzo Feligioni for helpful input on polishing and improving the manuscript.