Effect of neutrino electromagnetic properties on the quasielastic neutral-current neutrino-nucleus scattering

Exploring the fundamental physical properties of elementary particles remains one of the most significant scientific challenges, both theoretically and experimentally. Among these, the neutrino stands out as a particularly intriguing particle. Although nearly a century has passed since it was first postulated by Pauli in the context of double beta decay, many of its fundamental properties—such as its mass, electromagnetic characteristics, and cosmological roles, including those in various astrophysical environments—remain poorly understood. For example, the neutrino has long been considered as a potential candidate for dark matter. While neutrino flavor mixing is well established, the absolute mass scale of the neutrino remains unknown. Determining the precise mass of the neutrino is therefore an ongoing and central question in neutrino physics. Within the Standard Model (SM), neutrinos are assumed to be point-like particles with no internal structure [1]. However, testing the limits of this assumption has been a long-standing challenge. Recent theoretical developments and experimental results [2, 3] suggest that neutrinos may possess intrinsic properties such as a nonzero magnetic moment and a finite charge radius—features not accounted for within the SM framework.

The charge radius and magnetic moment—electromagnetic (EM) properties of neutrinos—offer a valuable window into testing the boundaries of the SM. Experimentally, there has been a long-standing effort to determine upper limits on these quantities using a variety of sources, including accelerator-based experiments [4–7], reactor neutrinos [8, 9], and solar neutrinos observed with modern detectors [10, 11]. However, the experimental results remain inconclusive and lack convergence. A comprehensive review in Ref. [12] summarizes the status of various experiments aimed at determining the upper limit of the neutrino magnetic moment through neutrino-electron scattering. The current upper limits on the neutrino magnetic moment span several orders of magnitude, ranging from $ 10^{-11} $ to $ 10^{-7}\,\mu_{\rm{B}} $, where $ \mu_{\rm{B}} $ denotes the Bohr magneton. In comparison, the charge radius is somewhat more constrained, typically on the order of $ 10^{-3}\,{\rm{fm}} $, although the exact magnitude varies across different measurements [13]. More recently, improved constraints on the EM properties of neutrinos have been obtained from coherent elastic neutrino-nucleus (ν-A) scattering (CEνNS) experiments [14, 15]. Nevertheless, it is worth noting that the current results remain close to previously established experimental bounds [16], indicating that only modest improvements have been achieved thus far.

Quasielastic (QE) ν-A scattering is a powerful probe for studying neutrino interactions within a nuclear medium. Accurate measurements from experiments such as MiniBooNE [17–20], MicroBooNE [21, 22], SciBooNE [23, 24], T2K [25, 26], and MINERνA [27, 28] necessitate precise modeling of the in-medium nucleon wave functions and their interactions with incident neutrinos. Recent studies have examined nuclear structure effects by analyzing uncertainties associated with the in-medium effective mass of the nucleon and the density dependence of the nuclear symmetry energy [29–31]. These works demonstrate that the influence of the nucleon effective mass can be distinctly identified, with theoretical results favoring an isoscalar effective mass close to the free-space nucleon mass, in better agreement with experimental data. Many observables are directly or indirectly influenced by both the effective mass and the symmetry energy. However, additional uncertainties can arise from other nuclear interactions, such as pairing forces and charge symmetry breaking. These effects could be significant in certain nuclei or for specific observables, and warrant further investigation in the context of lepton–nucleus scattering. Another major source of theoretical uncertainty stems from the axial mass of the nucleon in the nuclear medium. Using the standard value $ M_{\rm{A}} = 1.032 $ GeV, calculations of QE neutral-current (NC) scattering for both neutrinos and antineutrinos tend to underestimate the measured cross sections [32].

One limitation of QE ν-A scattering, compared to electron–nucleus scattering, lies in the energy resolution. While the energy of incident electrons can be tuned with high monoenergetic precision, the energy of neutrinos is inherently difficult to control. As a result, the neutrino energy spectrum is significantly broader than that of electrons, which can contribute to discrepancies between theoretical predictions and experimental data, particularly when using the standard axial mass value of $ M_A = 1.032 $ GeV. To account for contributions beyond the QE region, several processes have been studied in the literature, including meson exchange currents (MEC) [33, 34], particle–hole excitations [35, 36], pion production [37, 38], and final-state interactions (FSI) [39–41]. However, since the effects of neutrino EM properties are primarily associated with elastic channels and are largely independent of inelastic processes, the present study focuses on the contributions of the neutrino magnetic moment and charge radius to the electroweak NC scattering of neutrinos off nuclei.

In this work, we investigate the effects of the neutrino charge radius and magnetic moment on QE electroweak NC scattering of neutrinos off ¹²C. The nuclear wave function of the target nucleus is described within the framework of the quantum hadrodynamics (QHD) model, and we adopt the standard value of the axial mass, $ M_A = 1.032 $ GeV. In Ref. [42], the cross sections for charged-current QE ν-⁴⁰Ar scattering were computed using the same QHD model employed in this study. The results were compared with MicroBooNE experimental data [22], showing that the QHD model achieves comparable accuracy to leading neutrino event generators such as GENIE, NEUT, NuWro, GiBUU, and the MicroBooNE Monte Carlo [22].

In our calculations, we consider three representative values of the magnetic moment spanning different orders of magnitude, constrained by various experiments: the largest value, $ \mu_\nu = 2.13 \times 10^{-10} \mu_{\rm{B}} $, is reported by the CEνNS Collaboration [16]; the intermediate value, $ \mu_\nu = 2.9 \times 10^{-11} \mu_{\rm{B}} $, is from the GEMMA experiment [43]; and the smallest value, $ \mu_\nu = 6.3 \times 10^{-12} \mu_{\rm{B}} $, is derived from the XENONnT data [44]. For the neutrino charge radius, we adopt two values differing by roughly a factor of three: $ R^2_\nu = 5 \times 10^{-32}\,{\rm{cm}}^2 $, constrained by the CEνNS Collaboration [16], and $ R^2_\nu = 0.48 \times 10^{-32}\,{\rm{cm}}^2 $, reported by the BNL Collaboration [4]. By incorporating these EM properties into the QE scattering cross section, we assess their contributions to the differential cross section. More importantly, by comparing our theoretical results with experimental data [4, 16, 43], we can place constraints on the neutrino EM properties.

The structure of this paper is organized as follows. In Sec. II, we present the theoretical formalism to describe the electroweak NC scattering of neutrinos off ¹²C, formulated within the framework of the QHD model [45]. In particular, we incorporate the effects of the neutrino charge radius and magnetic moment into the scattering amplitude. Section III provides the numerical results and detailed discussions on the differential cross sections for various values of the neutrino magnetic moment and charge radius, as constrained by recent experimental data. Finally, a summary and concluding remarks are given in Sec. IV.

In this section, we present the theoretical framework for electroweak NC neutrino scattering off a nucleus in the QE regime, based on the QHD model. The formalism includes contributions from both the neutrino magnetic moment and charge radius. For QE inclusive electroweak NC ν-A scattering, we consider the target nucleus to be initially at rest at the origin of the coordinate system. The four momenta of the particles involved in the reaction are defined as follows: $ p_i^\mu = (E_i, {\bf{p}}_i) $ and $ p_f^\mu = (E_f, {\bf{p}}_f) $ for the incident and outgoing neutrino, respectively; $ p_A^\mu = (E_A, {\bf{p}}_A) $ for the initial (target) nucleus; $ p_{A-1}^\mu = (E_{A-1}, {\bf{p}}_{A-1}) $ for the residual nucleus; and $ p^\mu = (E_N, {\bf{p}}) $ for the knocked-out nucleon. We begin by introducing the general expression for the fivefold differential cross section for electroweak NC neutrino scattering off a nucleus—in this study, specifically for the $ ^{12}{\rm{C}} $ target—as the foundation for our subsequent analysis.

where $ M_A $, $ M_{A-1} $, and $ M_N $ are the target nucleus, residual nucleus, and nucleon masses, respectively. The $ \Omega_l $ and $ \Omega_N $ are, respectively, the scattering directions of the outgoing lepton and the outgoing nucleon. The recoil factor $ f_{\rm{rec}} $ is written as

where $ {\bf{q}}={\bf{p}}_f-{\bf{p}}_i $. Considering the EM properties of the neutrino in the electroweak NC scattering, the squared invariant matrix element is given by summing the weak, electromagnetic, and interference contributions

where the subscripts of $ {\rm{W}} $, $ {\rm{EM}} $, and $ {\rm{INT}} $ represent the weak, electromagnetic, and interference terms, respectively. If neutrino EM properties are neglected, i.e., $ \mu_\nu=0 $ and $ R_\nu=0 $, the EM and INT contributions are absent.

For a free nucleon, the NC operator comprises the weak, EM, axial-vector, and pseudoscalar form factors:

Here, $ F_1^{\rm{EM}} = 1 $ and $ F_2^{\rm{EM}} = \kappa_p $ for the proton, while $ F_1^{\rm{EM}} = 0 $ and $ F_2^{\rm{EM}} = \kappa_n $ for the neutron, with the four-momentum transfer defined as $ Q^2 = q^2 - \omega^2 $. The anomalous magnetic moments are given by $ \kappa_p = 1.793 $ and $ \kappa_n = -1.913 $, in units of the nuclear magneton $ \mu_N = e/(2M_N) $. According to the conservation of vector current hypothesis, and incorporating the isoscalar strange quark contribution $ F_i^s(Q^2) $, the vector form factors for the proton and neutron, $ F_i^{V,\; p(n)}(Q^2) $, are expressed as follows:

where $ \theta_W $ is the Weinberg angle given by $ \sin^2 \theta_W = 0.224 $. The strange vector form factors are given as

where $ \tau=Q^2/(4M_N^2) $, $ M_V=0.843 $ GeV, $ F_1^s (0) =-\langle r_s^2\rangle/6= 0.53 $ GeV^-2, and $ F_2^s(0)=\mu_s $ with the strange magnetic moment given by $ \mu_s=-0.4 $. The axial form factor is given as

We use the axial-vector coupling constant $ g_A = 1.262 $ and the axial mass $ M_A = 1.032 $ GeV throughout this work. The strange quark contribution to the nucleon axial form factor is taken as $ g_A^s = -0.19 $, representing the strange quark content in the nucleon. The signs $ (-,+) $, which arise from isospin dependence, correspond to the final-state nucleons being a proton or a neutron, respectively. We note that the pseudoscalar form factor $ G_P $ is neglected in the calculation because its contribution is proportional to $ m_l^2 / M_N^2 $, where $ m_l $ is the lepton mass in the final state.

Next, the operators for the neutrino weak and EM currents are given as follows [46–49]:

where $ f_m $ is written as $ f_m = f_1 + (m_{\nu}/m_e) f_2 $. $ m_{\nu} $ and $ m_e $ denote the neutrino and electron masses, respectively. $ f_1 $, $ g_1 $, $ f_2 $, and $ g_2 $ are the Dirac, anapole, magnetic, and electric form factors of the neutrino, respectively. The Dirac and anapole form factors are related to the vector and axial vector charge radii $ \langle R^2_V \rangle $ and $ \langle R^2_A \rangle $ through [46]

Neutrino charge radius is defined by $ \langle R_\nu^2 \rangle = \langle R^2_V \rangle + \langle R^2_A \rangle $ and then $ f_m + g_1 = {\dfrac 1 6} \langle R_\nu^2 \rangle Q^2 $. In the limit of $ Q^2 \rightarrow 0 $ (rest frame), $ f_2 (0) $ and $ g_2 (0) $ define the neutrino magnetic and electric dipole moment [48]

where $ \mu^2_{\nu} = (\mu^{m}_{\nu})^2 + (\mu^e_{\nu})^2 $ with the Bohr magneton $ \mu_B $. Note that the EM vertex form factors can arise in Beyond the Standard Model (BSM) models, such as heavy sterile mixing or loop-induced magnetic moments.

The neutrino tensor of the weak term is given by

for the EM term,

and for the interference contribution,

Within the laboratory frame, by choosing the three momentum transfer $ \bf q $ along the z-axis, the inclusive differential cross section of neutrino scattering off the nucleus in the electroweak NC reaction is given by the contraction between lepton and hadron tensors and integrating the cross section over the phase space of scattered (outgoing) lepton and outgoing nucleon:

where $ \theta_l $ is the scattering angle of the lepton, $ \theta_N $ is the polar angle of outgoing nucleons, T is the kinetic energy of the knocked-out nucleon, $ h=-1 $ and $ 1 $ correspond to the intrinsic helicity of the incident neutrino and antineutrino, respectively, and i denotes W, EM, and INT. For the NC reaction, the kinematic factors $ \sigma^{\rm{W}}_M $, $ \sigma^{\rm{EM}}_M $, and $ \sigma^{\rm{INT}}_M $ are respectively defined as

where $ M_Z = $ 91.19 GeV is the rest mass of the Z-boson. $ G_F = $ 1.166 $ \times 10^{-5} $ GeV^-2 denotes the Fermi constant and $ \alpha_{\rm{EM}} $ is the EM fine structure constant. The $ R_L $, $ R_T $, and $ R^{'}_T $ are the longitudinal, the transverse, and the transverse interference response functions. The appropriate response functions are written as

where $ N^\mu_i({\bf{q}}) $ is the Fourier transform of the nucleon transition current $ J^\mu_i({\bf{r}}) $

The nucleon transition current $ J^\mu_i ({\bf{r}}) $ is given by

where $ \psi_N $ and $ \psi_b $ are the wave functions of the outgoing nucleon and the bound state, respectively. The neutrino kinematic factors for the weak term are given by

for the EM part,

and for the interference term,

Using the QHD nuclear model, we investigate the role of the neutrino’s EM properties in NCQE scattering. Specifically, we calculate the single differential cross sections for NC ν–¹²C scattering as functions of the kinetic energy of the outgoing nucleon and the squared four-momentum transfer. For the neutrino charge radius, we consider two representative values: $ \langle R_\nu^2 \rangle \sim 5 \times 10^{-32}\, {\rm{cm}}^2 $, obtained from the combined analysis of the Dresden-II and COHERENT data [16], and $ \langle R_\nu^2 \rangle \sim 0.48 \times 10^{-32}\, {\rm{cm}}^2 $, the smallest known value reported by the BNL-E734 experiment [4]. For the neutrino magnetic moment, we adopt three benchmark values: $ \mu_\nu \sim 2.13 \times 10^{-10}\, \mu_{\rm{B}} $ from Dresden-II, $ \mu_\nu \sim 2.9 \times 10^{-11}\, \mu_{\rm{B}} $ from the GEMMA experiment [43], and $ \mu_\nu \sim 6.3 \times 10^{-12}\, \mu_{\rm{B}} $, the smallest value considered, derived from XENONnT data [44]. The specific values of $ \langle R_\nu^2 \rangle $ and $ \mu_\nu $ used in this study are summarized in Table 1.

	$ \langle R_\nu^2 \rangle $ [cm2]	$ \mu_\nu/\mu_B $
case 1	$ 5\times 10^{-32} $ [16]	$ 2.13\times 10^{-10} $ [16]
case 2	$ 0.48 \times 10^{-32} $ [4]	$ 2.13\times 10^{-10} $ [16]
case 3	$ 5\times 10^{-32} $ [16]	$ 2.9\times 10^{-11} $ [43]
case 4	$ 0.48 \times 10^{-32} $ [4]	$ 2.9\times 10^{-11} $ [43]
case 5	$ 5 \times 10^{-32} $ [16]	$ 6.3\times 10^{-12} $ [44]

Table 1.  Various combinations of the charge radii and magnetic moments for the neutrino for the present numerical estimations

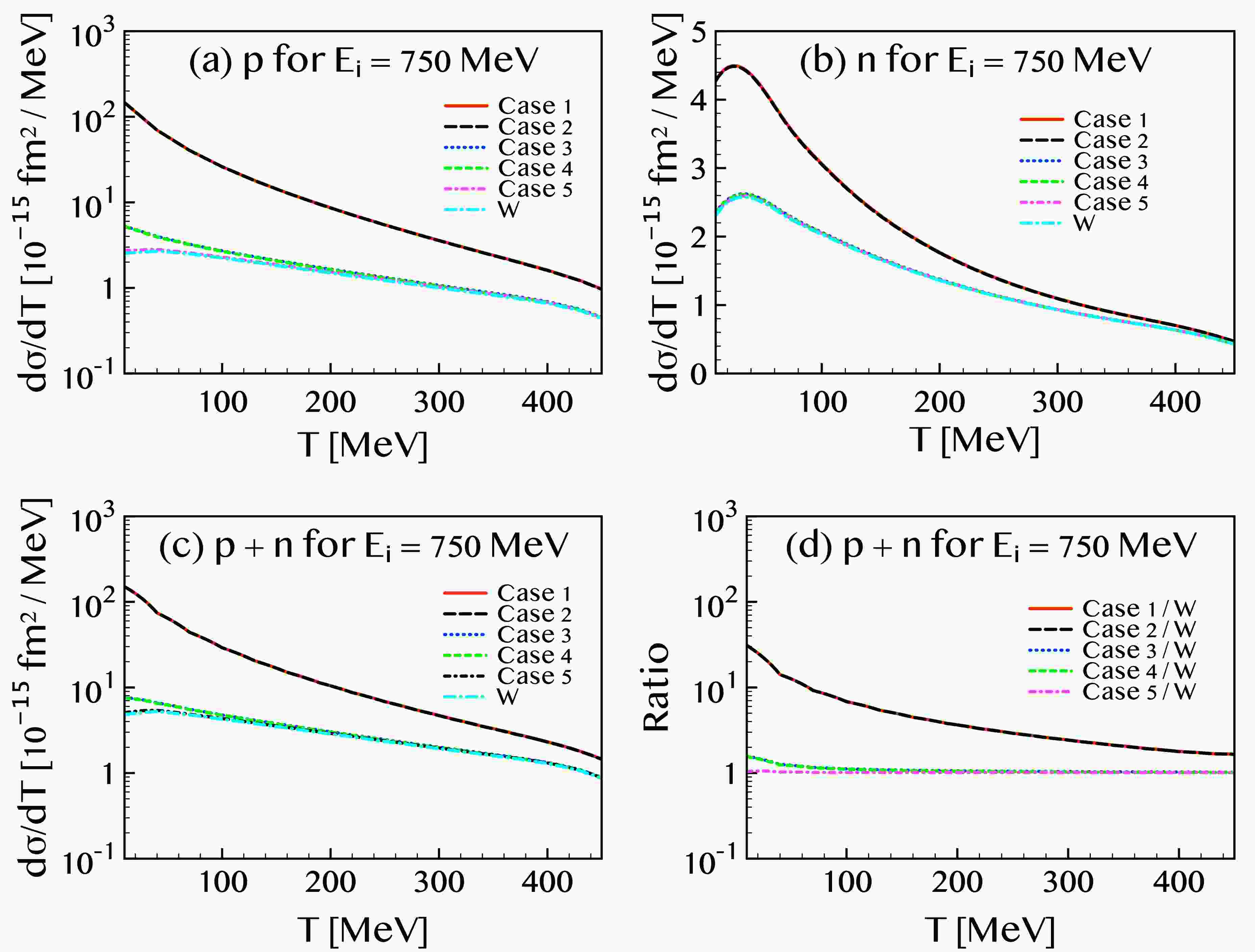
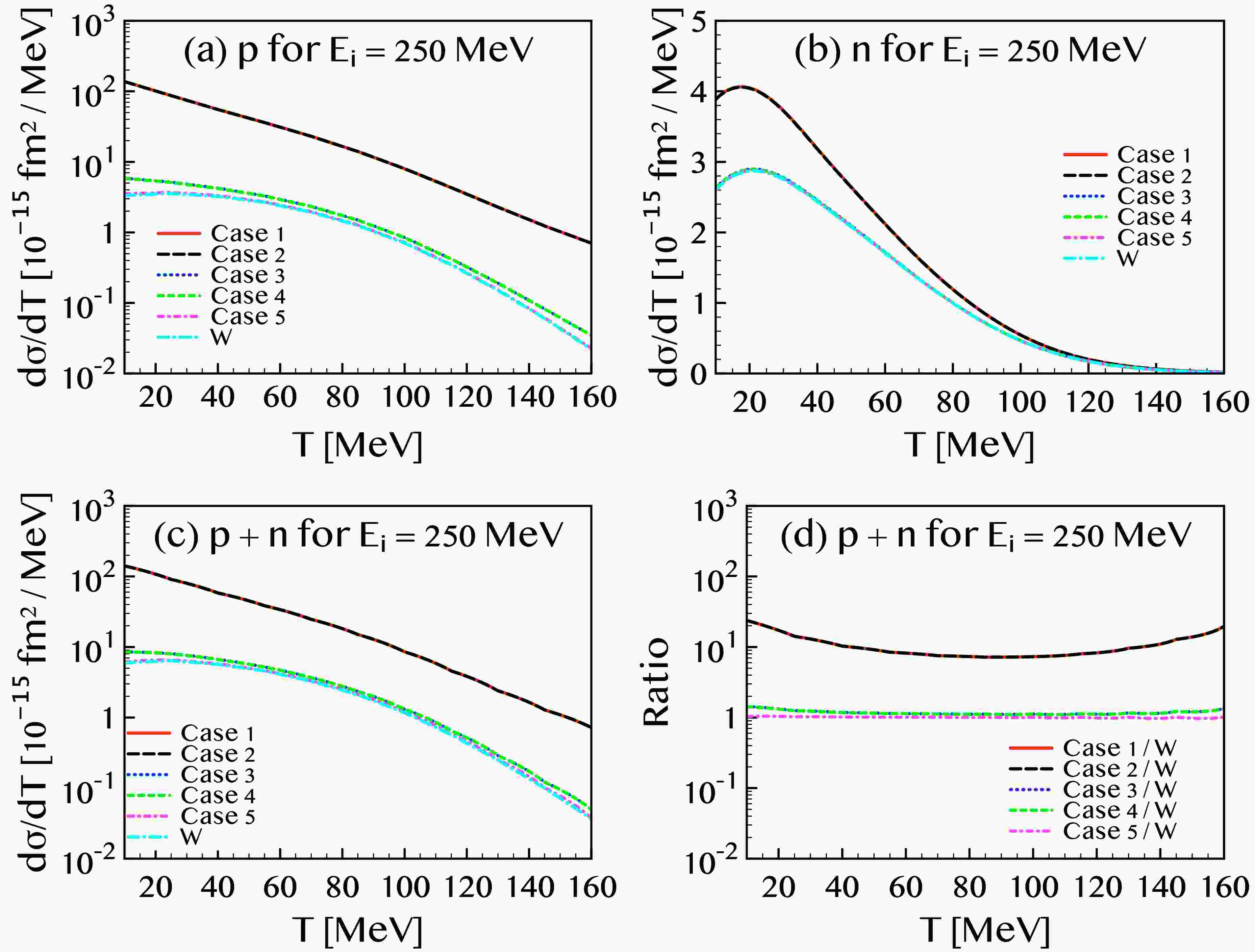
Shown in Figs. 1 and 2 are the single differential cross sections plotted as functions of the kinetic energy of the final-state nucleon for incident neutrino energies $ E_i = 250 $ and 750 MeV, respectively. The solid (red) curves correspond to case 1, the dashed (black) to case 2, the dotted (blue) to case 3, the short-dashed (green) to case 4, and the dot-dashed (magenta) to case 5. Panels (a) and (b) show the separate contributions from the proton and neutron knockout, respectively, while panel (c) displays the total cross section as the sum of both contributions. Panel (d) exhibits the value of each case divided by the value without neutrino EM properties which is denoted by `W'. The differences between the red and black curves, as well as between the blue and green curves, are minimal, less than 1 %, indicating that the effect of the neutrino charge radius on the cross section is negligible. In contrast, the difference between the red (or black) curves and the blue (or green) ones is substantial, with the dominant source of deviation attributed primarily to the proton contribution.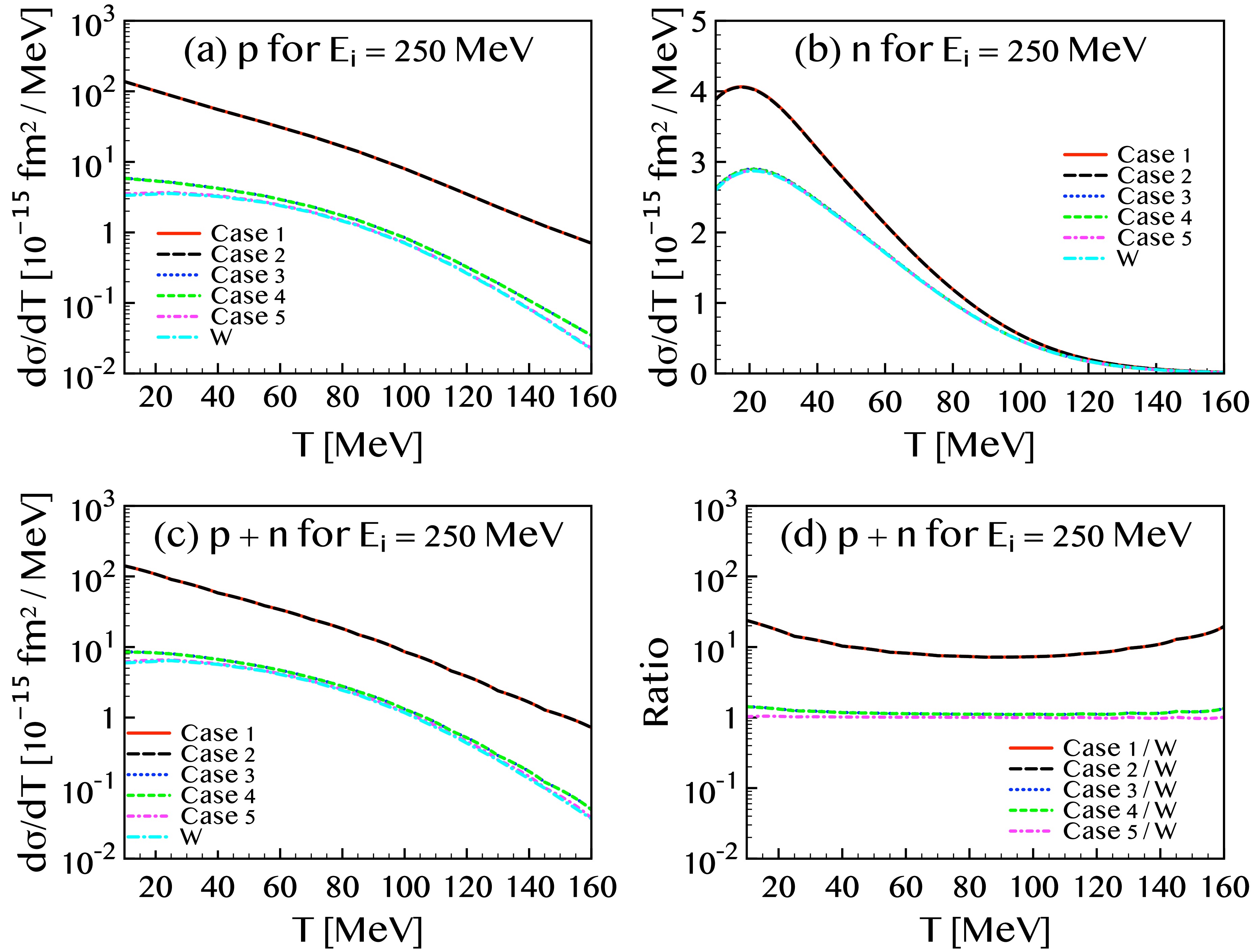

Figure 1.  (color online) Differential cross sections for the $ (\nu, \nu') $ NC reaction on a ¹²C target as functions of the kinetic energy T of the outgoing nucleon, calculated for an incident neutrino energy of $ E_i = 250 $ MeV. The solid (red), long-dashed (black), dotted (blue), dashed (green), and dot-dashed (magenta) curves correspond to cases 1 through 5, respectively. The dot-long-dashed (cyan) curves labeled as `W' represent results obtained without including the electromagnetic (EM) properties of the neutrino. Panels (a), (b), and (c) show the proton-only, neutron-only, and total (proton + neutron) contributions, respectively. Panel (d) displays the cross sections in panel (c) divided by the values without neutrino EM properties.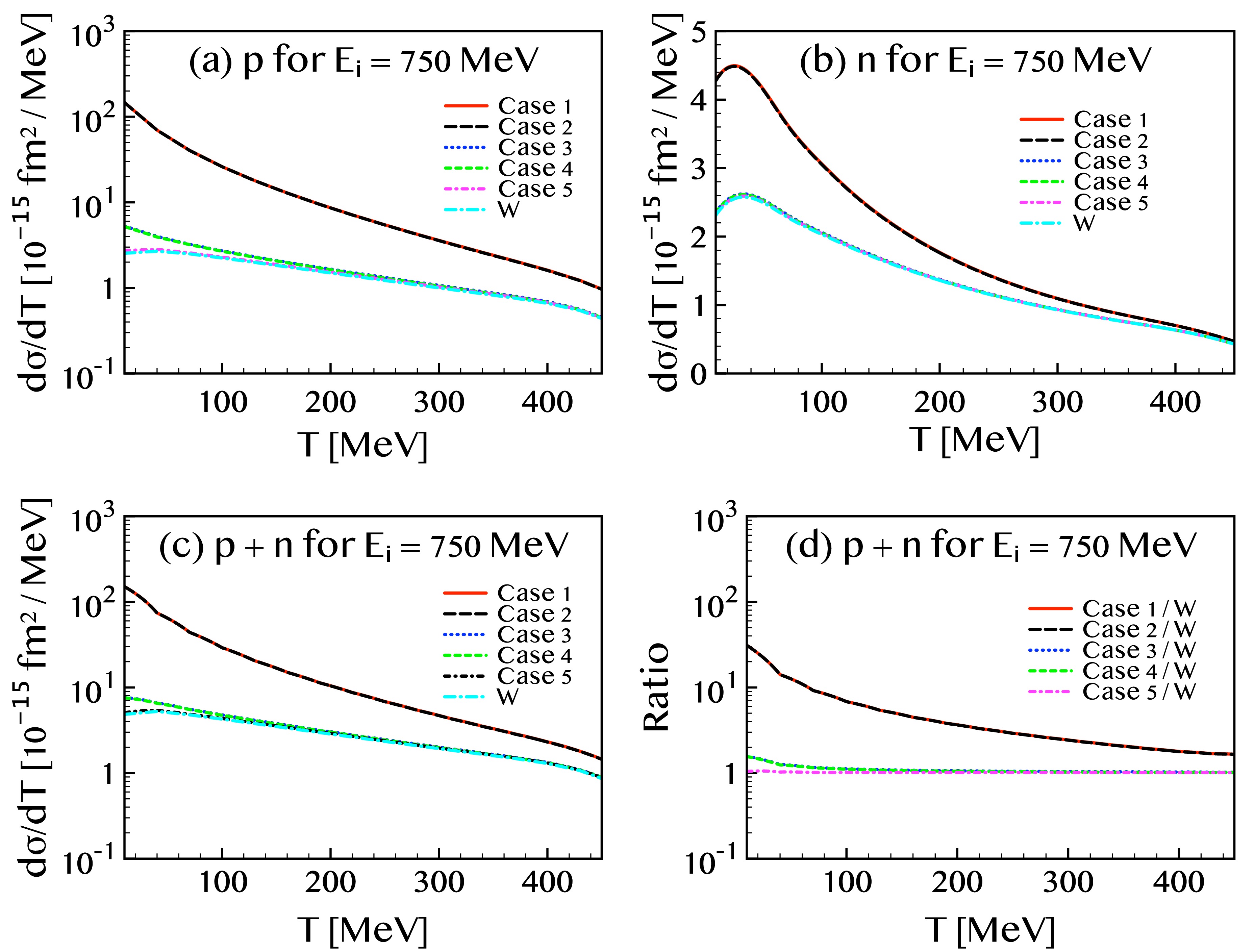

Figure 2.  (color online) The same as the Fig. 1 but with the incident neutrino energy $ E_i=750 $ MeV.

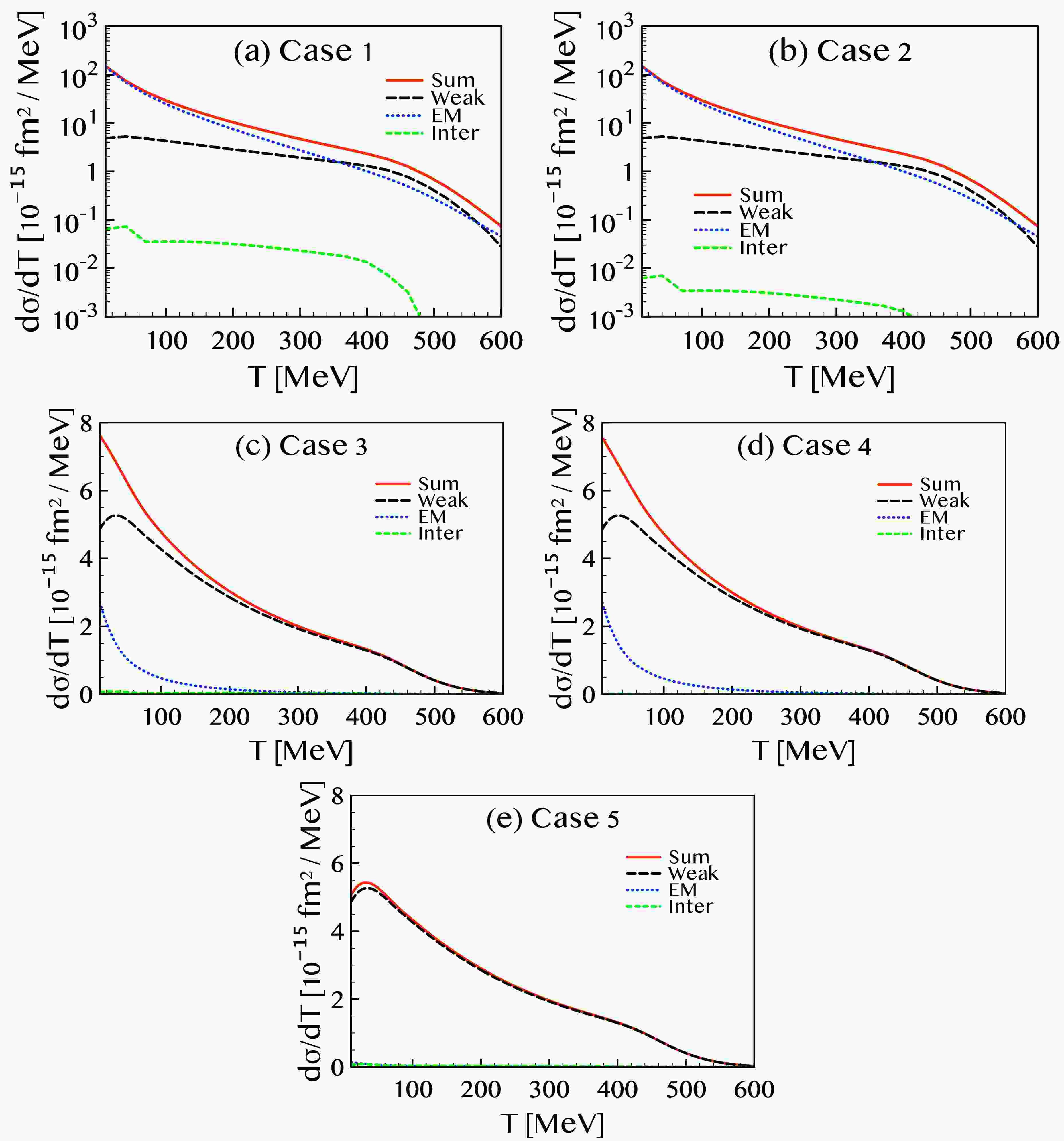
For the smallest magnetic moment value, $ \mu_\nu = 6.3 \times 10^{-12}\, \mu_{\rm{B}} $, the contributions from the proton and neutron are comparable in magnitude. For the intermediate value, $ \mu_\nu = 2.9 \times 10^{-11}\, \mu_{\rm{B}} $, which is approximately 4.6 times larger than the smallest value, the neutron contribution remains nearly unchanged, while the proton contribution increases significantly at lower kinetic energies. At $ T \approx 10 $ MeV, the proton cross sections for cases 3 and 4 are approximately twice of those for case 5. With the largest magnetic moment value, $ \mu_\nu = 2.13 \times 10^{-10}\, \mu_{\rm{B}} $, the neutron cross section increases by factors of approximately 1.5 and 1.9 for $ E_i = 250 $ and 750 MeV, respectively, relative to the intermediate case. However, for the proton, the enhancement is much more dramatic: the cross section with the largest $ \mu_\nu $ exceeds that of the intermediate value by more than a factor of 20. As a result, at $ T\approx 10 $ MeV, the total cross sections for cases 3 and 4 are about 1.6 times larger than those of case 5, while those of cases 1 and 2 are enhanced by more than an order of magnitude relative to cases 3 and 4.

To better understand the origin of this significant enhancement, particularly in the proton channel, we next analyze the individual contributions from the weak, electromagnetic, and interference terms in the cross section. In Fig. 3, we depict the contribution of each term in the cross section formula given in Eq. (16) at an incident neutrino energy of $ E_i = 750 $ MeV. The solid (red) curves represent the total differential cross section obtained by summing all contributions, the dashed (black) curves correspond to the weak interaction only, the dotted (blue) curves show the EM interaction contribution, and the short-dashed (green) curves represent the interference between weak and EM interactions. Panels (a) through (e) correspond to case 1 through case 5, respectively. In the low kinetic energy region of the outgoing nucleon (T), the EM interaction dominates for cases 1 and 2, whereas the weak interaction dominates for cases 3, 4, and 5. The cross section is susceptible to the neutrino magnetic moment but remains insensitive primarily to the charge radius, consistent with previous observations. Nonetheless, a small dependence on the charge radius can be identified by comparing the interference terms in Figs. 3(a) and 3(b). The interference contribution in panel (a) is approximately an order of magnitude larger than that in panel (b), which corresponds closely to the ratio of the $ \langle R^2 \rangle $ values between the two cases. However, this effect is negligible in both the weak and EM contributions, implying that the total cross section is practically unaffected by variations in the charge radius.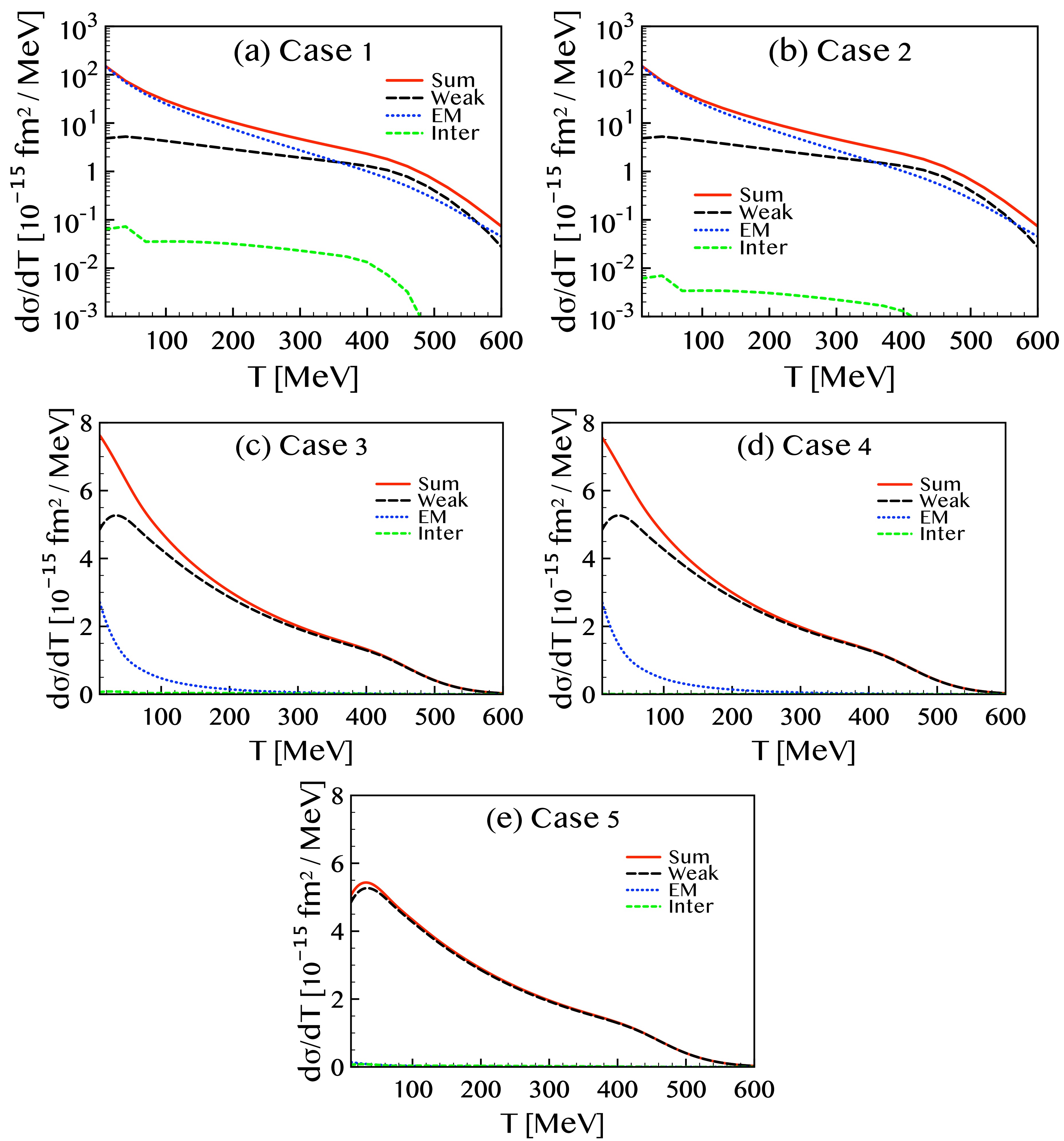

Figure 3.  (color online) Breakdown of the differential cross sections for the $ (\nu, \nu') $ NC scattering as functions of the knocked-out nucleon kinetic energy T, at an incident neutrino energy of $ E_i = 750 $ MeV. The long-dashed (black), dotted (blue), and dashed (green) curves represent the contributions from the weak, EM, and interference terms, respectively, while the solid (red) curves show the total differential cross sections obtained by summing all contributions. Panels (a)–(e) correspond to cases 1 through 5, respectively.

A particularly striking result arises in the EM contribution. For $ \mu_\nu = 2.13 \times 10^{-10}\, \mu_{\rm{B}} $, as used in Figs. 3(a) and 3(b), the weak contributions remain unchanged relative to those for smaller $ \mu_\nu $ values. However, the EM contribution experiences a dramatic enhancement for $ T\lesssim 500 $ MeV, and it becomes the dominant component of the total cross section for $ T\lesssim 300 $ MeV. When $ \mu_\nu = 2.90 \times 10^{-11}\, \mu_{\rm{B}} $, the EM term is negligible at $ T \gtrsim 200 $ MeV, but becomes significant at $ T \lesssim 100 $ MeV, contributing up to 40 % of the weak term near threshold. In contrast, for the smallest value $ \mu_\nu = 6.3 \times 10^{-12}\, \mu_{\rm{B}} $, the EM contribution remains perturbative at all energies, and the total result closely resembles that of the weak-only case. In summary, the influence of the neutrino magnetic moment is evident in the differential cross section at low outgoing nucleon energies. As shown in the following figure, this enhancement at low energies plays a crucial role in improving the agreement with experimental data.

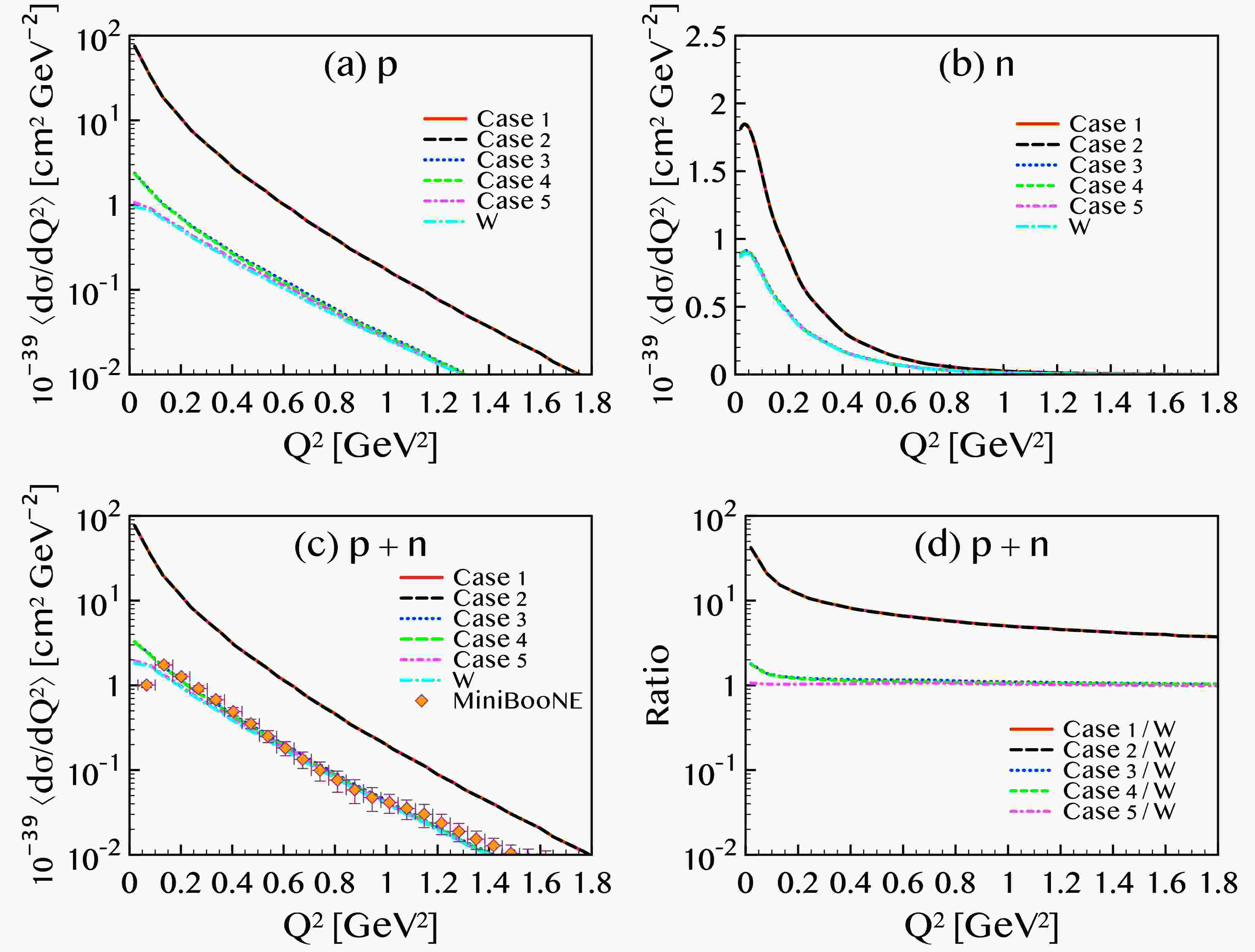
The observed enhancement of the EM contribution can be understood from Eqs. (26)–(28). The dominant terms arise from the second terms in Eqs. (26) and (27), which scale as $ [(p_i + p_f)/m_e]^2 $ and $ (Q/m_e)^2 $, respectively. Due to the small electron mass in the denominator, these terms are significantly amplified at the energies considered in this study. Furthermore, since the magnitude of $ f_2 $ is much greater than that of $ g_2 $, the form factor $ f_2 $ dominates the EM contribution. The magnetic moment $ \mu_\nu $ in cases 1 and 2 is larger than in cases 3 and 4 by a factor of approximately 7.3. Consequently, the enhancement of the proton cross section due to EM terms is greater than that for the neutron by a factor of about $ 7.3^2\approx 53 $, consistent with the result shown in Fig. 3.

Figure 4 shows the flux-averaged single differential cross section as a function of the squared four-momentum transfer $ Q^2 $, calculated for five different cases of the neutrino charge radius and magnetic moment, as in Fig. 1. The results are compared with the MiniBooNE experimental data [18]. Panels (a) and (b) display the separate contributions from the proton and neutron knockout, respectively. As observed in the previous results, the effect of the charge radius remains negligible, whereas the magnetic moment plays a crucial role in shaping the cross section. In panel (c) that shows the sum of proton and neutron, the red and black curves, corresponding to larger magnetic moments, show good agreement with the data at $ Q^2 \gtrsim 1\,({\rm{GeV}}/c)^2 $. However, they overestimate the cross section in the low-$ Q^2 $ region. In contrast, the blue and green curves—associated with $ \mu_\nu = 2.9 \times 10^{-11}\,\mu_{\rm{B}} $—consistently underestimate the experimental values. While the discrepancy is large at high $ Q^2 $, it gradually diminishes as $ Q^2 $ decreases.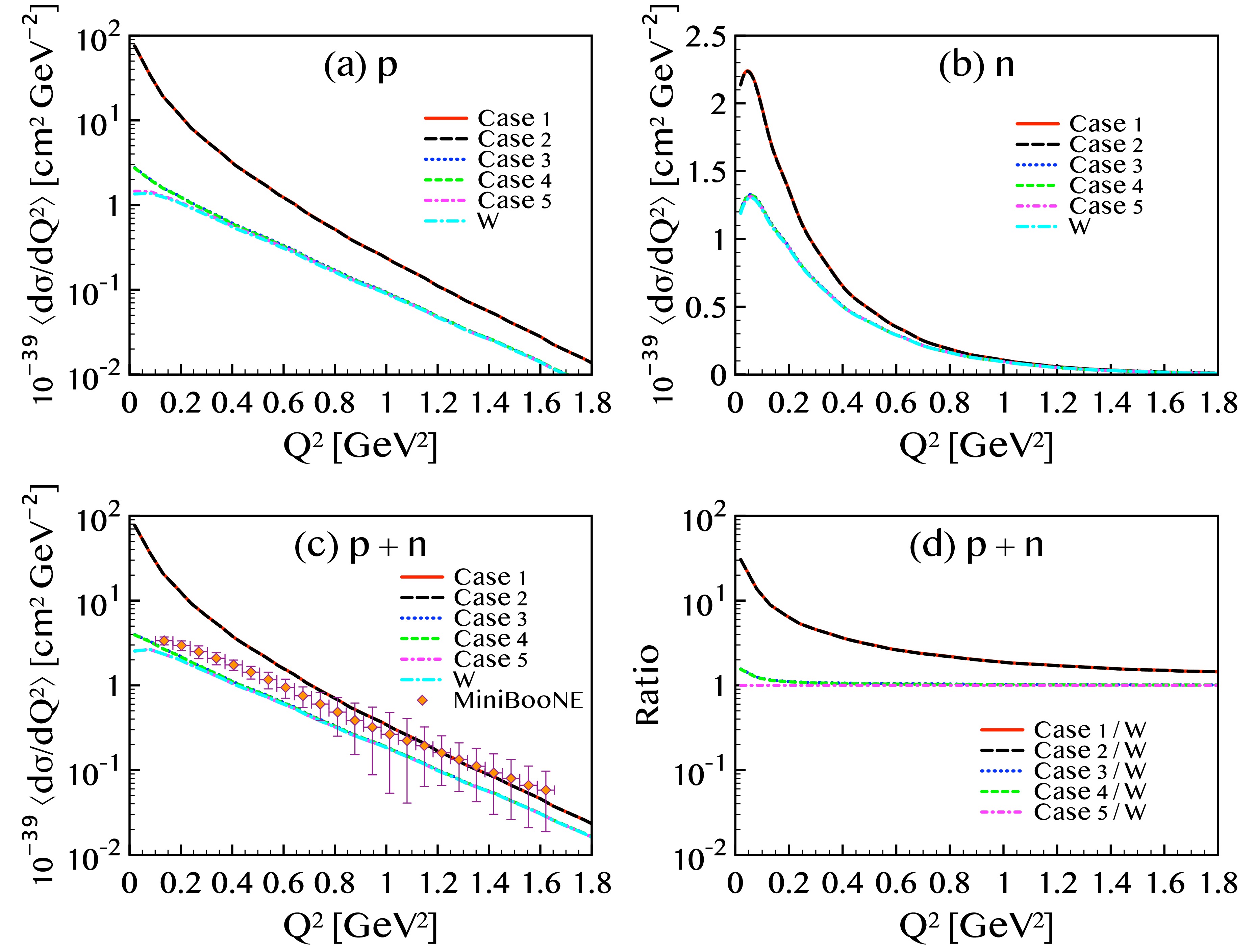

Figure 4.  (color online) The flux-averaged differential cross sections of $ ^{12}{\rm{C}}(\nu,\nu') $ are compared with the experimental data measured from [18].

When neutrino EM properties are not included, the results coincide with the purely weak interaction predictions shown previously in Fig. 3. The case with $ \mu_\nu = 2.13 \times 10^{-10}\,\mu_{\rm{B}} $ reproduces the data well at large $ Q^2 $, but exhibits an unphysical divergence at small $ Q^2 $, implying that smaller values of $ \mu_\nu $ may be more appropriate. For $ \mu_\nu = 2.9 \times 10^{-11}\,\mu_{\rm{B}} $, the EM contribution is negligible at high energies but significantly enhances the cross section at low energies, resulting in better agreement with the experimental data. In particular, in the low-$ Q^2 $ region, the magnetic moment helps reduce the discrepancy between theoretical predictions and experimental results. At the smallest $ Q^2 $ data point, $ Q^2 \approx 0.13\,({\rm{GeV}}/c)^2 $, the EM contribution increases the cross section by approximately 16 %, yet the prediction remains about 18 % below the measured value. This indicates that values of $ \mu_\nu $ larger than $ 2.9 \times 10^{-11}\,\mu_{\rm{B}} $ could reproduce the data more accurately. Values of $ \mu_\nu $ that are consistent with the MiniBooNE data will be considered in Fig. 6. In contrast, for $ \mu_\nu = 6.3 \times 10^{-12}\,\mu_{\rm{B}} $, the enhancement from the EM contribution is only about 1.7 %, highlighting the strong sensitivity of the cross section to the magnetic moment magnitude.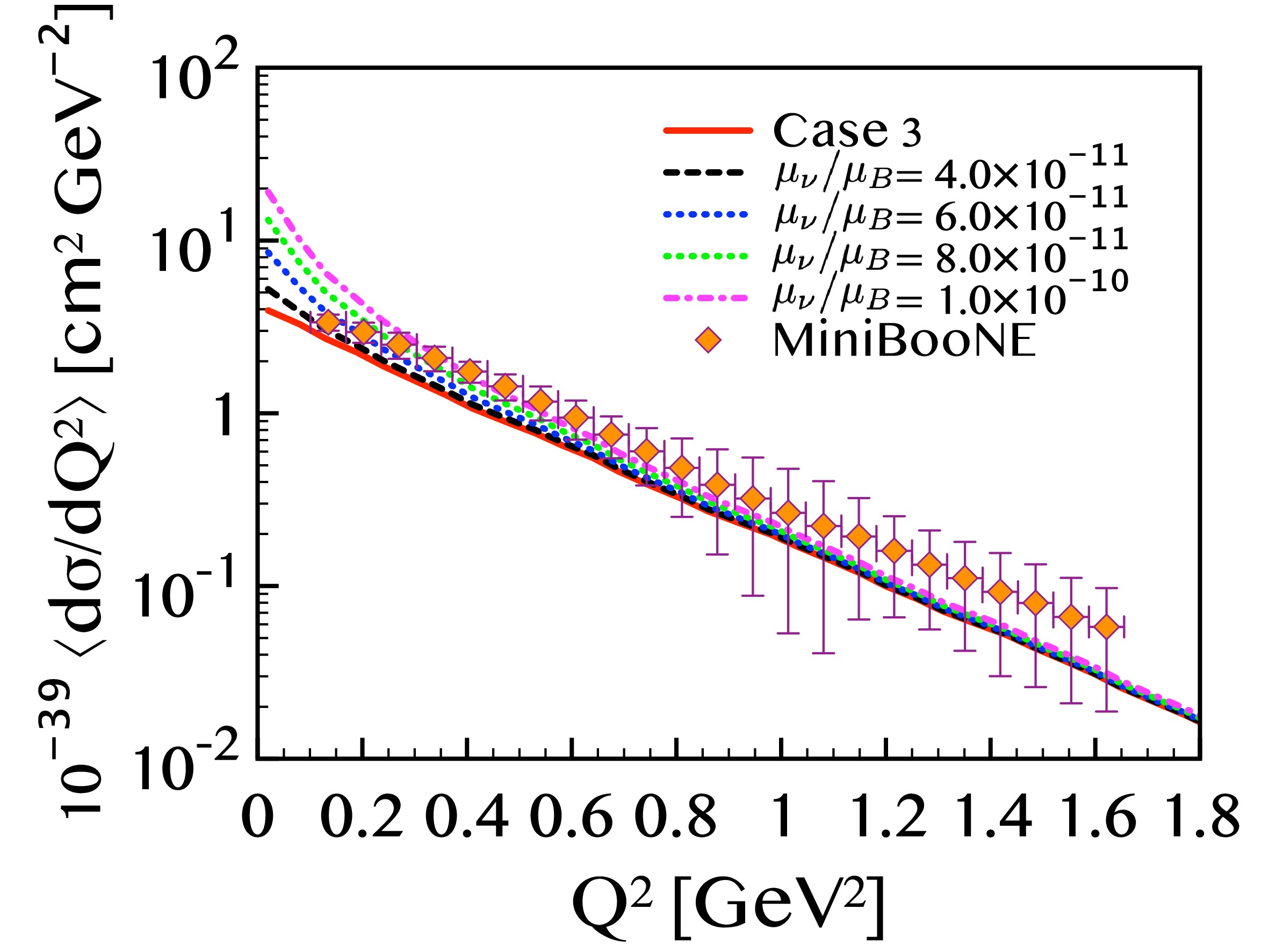

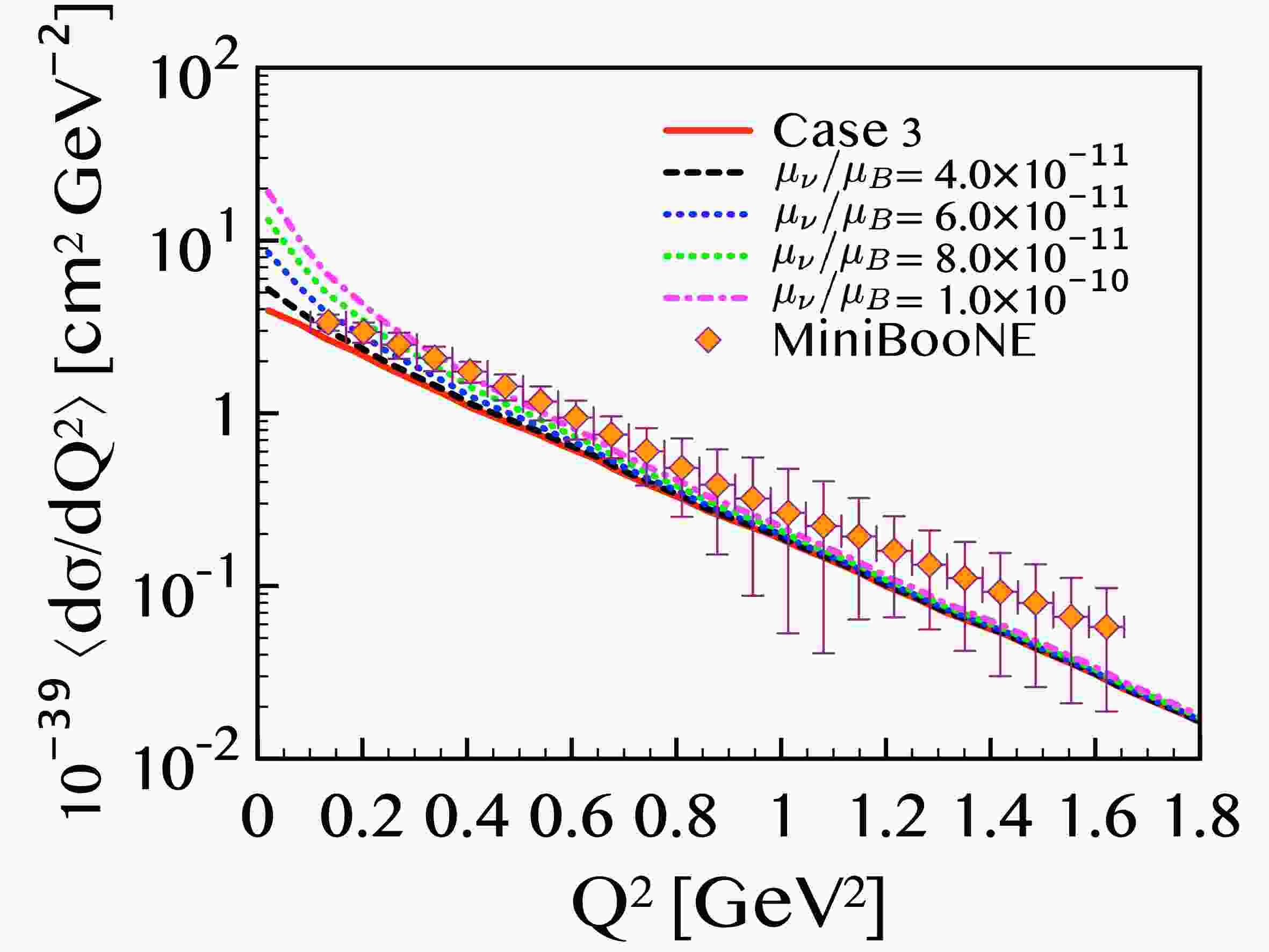
Figure 6.  (color online) The flux-averaged differential cross sections of $ ^{12}{\rm{C}}(\nu,\nu') $ with different values of $ \mu_\nu $. Charge radii are fixed to the value of case 3.

At high momentum transfer, the magnetic moment alone is insufficient to resolve the discrepancy between theory and experiment. In this regime, contributions from inelastic processes are expected to play a dominant role in bridging the gap. Some residual discrepancy at high $ Q^2 $ may arise from unaccounted inelastic channels such as $ 2p $-$ 2h $ or pion production, which are not modeled here.

At small $ Q^2 $ limit, scattering is basically elastic, and on top of that, nuclear excitations can play a certain role. It can either reduce or increase the discrepancy between the theory and experiment in the small $ Q^2 $ region. However, the calculation method and tools in the elastic scattering are different from those of QE scattering, so considering the non-QE effect at small $ Q^2 $ limit exceeds the scope of this work.

MiniBooNE Collaboration reported the measurement of NCQE antineutrino ($ \bar{\nu} $) scattering off ¹²C in Ref. [20]. Differenrence between ν and $ \bar{\nu} $ in the scattering formula is helicity, $ -1 $ and 1 for ν and $ \bar{\nu} $, respectively. Therefore, we can apply the equations developed in Sect. 2 to the $ \bar{\nu} $ NCQE scattering with non-vanishing charge radius and magnetic moment. Because experimental limits for the charge radius and magnetic moment are not measured yet for $ \bar{\nu} $, we assume the same values of the charge radius and magnetic moment of ν for $ \bar{\nu} $.

Figure 5 shows the result of $ \bar{\nu} $ NCQE scattering cross sections and they are compared with the MiniBooNE data [20]. Legends and conventions for the panels are the same with Fig. 4. Shape of curves for the proton and neutron contributions in Fig. 5 (a) and (b) are similar to those of the neutrino in Fig. 4 (a) and (b). Looking into details, however, one can see that the magnitude is significantly different between ν and $ \bar{\nu} $. In most cases of the charge radius and magnetic moment and at most values of $ Q^2 $, cross section of $ \bar{\nu} $ is suppressed to that of ν. Exception is the cases 1 and 2 for proton at $ Q^2 \simeq 0 $, where ν and $ \bar{\nu} $ are similar in magnitude. Suppression in the $ \bar{\nu} $ cross section leads to good agreement with MiniBooNE data in a wide range of the momentum transfer $ 0.1 \lesssim Q^2 \lesssim 1.2 $ (GeV/c)². A critical difference from ν is that while cases 1 and 2 reproduce data at high $ Q^2 $ for ν, results of $ \bar{\nu} $ in the cases 1 and 2 overshoot the data by orders of magnitude. On the other hand, for the cases 3 and 4, inclusion of the charge radius and magnetic moment does not alter the cross section at intermediate and high $ Q^2 $ values, but sizable effect appears at $ Q^2 \lesssim 0.2 $ (GeV/c)². As a result, the enhancement by the magnetic moment makes the theory agree with the data at $ 0.1 \leq Q^2 \leq 0.17 $ (GeV/c)², where the result with only weak contribution is outside the error range. Similar to ν, EM properties are advantageous in reducing the discrepancy between theory and experiment at low $ Q^2 $ region for $ \bar{\nu} $. Agreement with the MiniBooNE data of $ \bar{\nu} $-A scattering can be interpreted as a guidance for the upper limit of the $ \bar{\nu} $ magnetic moment. According to the result in Fig. 5, the upper limit of $ \mu_{\bar{\nu}} $ is around $ 3 \times 10^{-11} \mu_B $.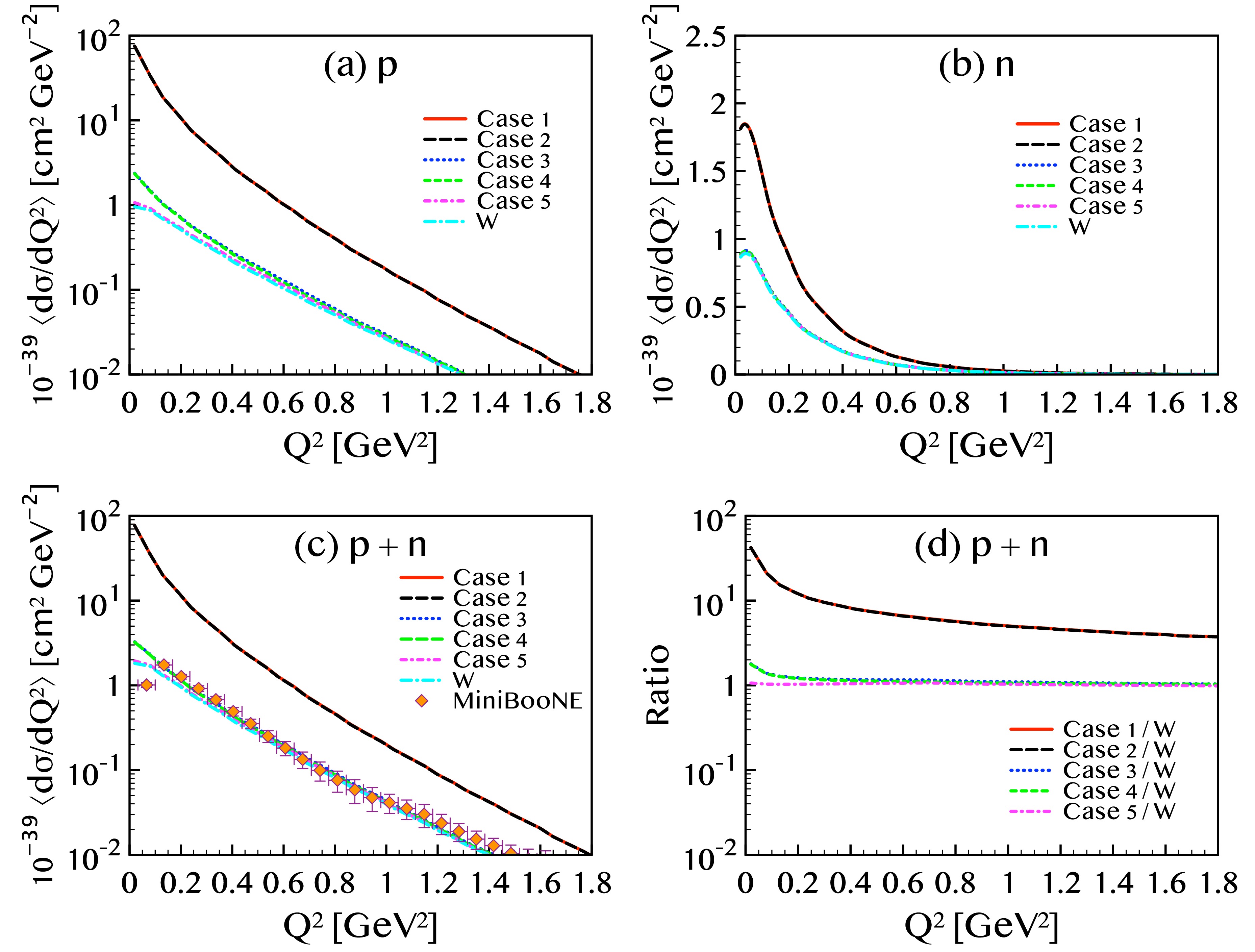

Figure 5.  (color online) The flux-averaged differential cross sections of $ ^{12}{\rm{C}}(\bar{\nu},\bar{\nu}') $ are compared with the experimental data measured from [20].

In Fig. 4, we have seen that there is a systematic discrepancy between theory and measurement for the NCQE ν-A scattering. In the genuine QE region, non-QE effects such as nuclear excitations, meson-exchange currents and pion productions cannot compensate the discrepancy. Neutrino EM properties could be a source to reduce the gap between theory and experiment in the QE region. We calculate the ν-A cross section by changing the EM properties of the neutrino to find the values that are consistent with MiniBooNE ν-A data. It is worth noting that, as shown and discussed in Figs. 1, 2, 4 and 5, the cross sections are insensitive to the charge radius and the result barely changes even though the charge radius differs by a factor of three. For this reason and for the sake of simplicity, we fix the charge radius to $ \left< R^2_\nu \right> = 5 \times 10^{-32}\, {\rm{cm}}^2 $ and consider the variation of the magnetic moment.

Figure 6 presents the result. Since $ \mu_\nu=2.9\times 10^{-11} \mu_B $ in case 3 underestimates the experimental data, we consider $ \mu_\nu $ in the range $ (0.4 - 1.0) \times10^{-10}\mu_B $ with five different values. As seen in Fig. 4, case 3 reproduces the data at $ Q^2 \geq 0.8 $ (GeV/c)², but underestimates the measurement in the QE resgion $ 0.3 \lesssim Q^2 \lesssim 0.8 $ (GeV/c)². The cross section in $ Q^2 \geq 0.8 $ (GeV/c)² is weakly affected by the increase of the magnetic moment: change in the cross section is negligible for $ \mu_\nu = 4\times10^{-11}\mu_B $ and $ 6 \times10^{-11}\mu_B $, and minor enhancement occurs for $ \mu_\nu = 8 \times10^{-11}\mu_B $ and $ 1\times10^{-10}\mu_B $. The curve for $ 6 \times10^{-11}\mu_B $ is located at the lower limit of the datum at $ 0.649 \leq Q^2 \leq 0.709 $ (GeV/c)², and it is below the data at lower $ Q^2 $ values. Larger values are favorable for better agreement with data in the QE region.

Results with $ 8 \times10^{-11}\mu_B $ and $ 1 \times10^{-10}\mu_B $ are more interesting. With these magnetic moments, theory results are within the most of the data in $ 0.3 \lesssim Q^2 \lesssim 0.8 $ (GeV/c)². For the datum at $ 0.236 \leq Q^2 \leq 0.304 $ (GeV/c)², cross sections with $ \mu_\nu = 8\times10^{-11}\mu_B $ pass the center of the error box, and those with $ \mu_\nu = 1\times10^{-10}\mu_B $ are located at the upper limit of the error bar. At one step lower $ Q^2 $ values $ 0.169 \leq Q^2 \leq 0.236 $ (GeV/c)², $ \mu_\nu = 8\times10^{-11}\mu_B $ gives a result at the upper limit of the error bar, and $ \mu_\nu = 1\times10^{-10}\mu_B $ overshoots the datum. Summarizing, theory results reside at the lower limit of datum at $ 0.642 \leq Q^2 \leq 0.709 $ (GeV/c)² with $ \mu_\nu = 8\times10^{-11}\mu_B $, pass upper limit limit of datum at $ 0.236 \leq Q^2 \leq 0.304 $ (GeV/c)² with $ \mu_\nu = 1\times10^{-10}\mu_B $, and satisfy the data between these $ Q^2 $ ranges. Therefore, $ \mu_\nu $ values that are consistent with the data in the QE region are $ 0.8 \lesssim \mu_\nu \lesssim 1.0 $ in units of $ 10^{-10} \mu_B $.

In the present work, we calculate the NCQE ν-A scattering off ¹²C within a relativistic nuclear model. To ensure current conservation and gauge invariance, the wave functions of the continuum nucleons are obtained by solving the Dirac equation using the same scalar and vector potentials as those applied to the bound nucleons. It is noted that inelastic contributions, such as particle–hole excitations and other channels, are not included in this analysis. The single differential cross sections are evaluated for five different cases involving variations in the neutrino charge radius and magnetic moment, expressed as functions of the kinetic energy of the knocked-out nucleon. The influence of the charge radius on the cross sections is found to be minimal, with no practically discernible differences across the tested values. In contrast, the magnetic moment has a significant impact, particularly at low kinetic energies.

The cross section for the proton exhibits a stronger dependence on the magnetic moment than that for the neutron, and this effect becomes more pronounced at lower nucleon energies. For instance, at an incident neutrino energy of $ E_i = 250 $ MeV, increasing the magnetic moment from $ \mu_\nu = 2.9 \times 10^{-11}\, \mu_{\rm{B}} $ to $ \mu_\nu = 2.13 \times 10^{-10}\, \mu_{\rm{B}} $ enhances the neutron cross section by approximately 50 % at $ T \approx 10 $ MeV. However, under the same conditions, the proton cross section increases by a factor of several tens. Moreover, for $ \mu_\nu = 2.9 \times 10^{-11}\, \mu_{\rm{B}} $, the EM contribution can reach up to 60 % of the weak contribution at small momentum transfer. As a consequence, the inclusion of neutrino EM properties helps reduce the discrepancy between the standard weak-only predictions and the MiniBooNE experimental data, improving agreement particularly at low momentum transfer. In contrast, for the smaller value $ \mu_\nu = 6.3 \times 10^{-12}\, \mu_{\rm{B}} $, the EM contribution is significantly suppressed. While still non-negligible, its overall impact becomes marginal. We note that the neutrino EM contributions to the lepton tensors are calculated independently of the nuclear wave functions (Eqs. (14, 15)). Therefore, behavior of the neutrino EM contribution obtained with the QHD model such as high sensitivity to the magnetic moment and negligible effect from the charge radius does not change even if we consider other nuclear models for the description of hadron parts.

Restricting to the QE region $ (0.3 \lesssim Q^2 \lesssim 0.8 $ (GeV/c)²), we obtain that the value of magnetic moment $ \mu_{\nu} $ consistent with the MiniBooNE data is between $ 0.8 \times 10^{-11} \mu_B $ and $ 1.0 \times 10^{-10} \mu_B $ in our calculation.

In conclusion, within the currently allowed experimental bounds on the neutrino’s electromagnetic properties, their effects manifest notably in QE ν-A scattering, especially at low energies of the outgoing nucleons and in the small momentum transfer regime.