Exploring Shape (phase) Evolution in even-even ^126−136Ba

Nuclear structure at high spin is typically described by a semiclassical model of a rotating average field, where an intrinsic shape rotates uniformly around a fixed spatial axis, representing rotation as a specific collective motion in finite many-body systems [1]. The physical consequences of such motion are influenced by shape asymmetry, characterized by the lowest order of quadrupole and triaxial deformations, which affect the time dependence of the nuclear and Coulomb fields [2, 3]. Most deformed nuclei exhibit axial symmetry in their ground states, whether oblate or prolate, allowing collective rotation only around the perpendicular axis. However, some nuclei have been observed to have triaxial ground-state deformations, as indicated by nuclear mass analyses [4]. In particular, nuclei in the $ A\approx 130 $ mass region are known to exhibit axial asymmetry in their ground states [5]. In this region, the proton Fermi surface lies in the lower part of the $ h_{11/2} $ orbitals, favoring a prolate shape, while neutrons occupy medium- to high-Ω orbitals in the same shell, potentially driving the shape toward an oblate configuration [6]. The competition between these opposing tendencies can result in a shape resembling a triaxial ellipsoid.

In a triaxially deformed potential, particles and holes tend to align their angular momenta along the short and long axes, respectively. According to the hydrodynamical model of rotation [3], the moment of inertia along the medium axis is the largest, favoring collective rotation around this axis. Consequently, the total angular momentum vector has nonzero components along all three principal axes [7]. For a triaxial nucleus, rotation can occur around any of the three principal axes. Principal axis cranking calculations reveal that rotation can indeed take place around any of these axes, corresponding to three different minima in the total energy surface in the ($ \beta_2, \gamma $) plane [8]. However, the rotational axis of a triaxial nucleus typically coincides with the principal axis that has the largest moment of inertia, leading to the lowest-energy (yrast) states.

Along the yrast states, transitions can occur between rotations characterized by varying relationships between aligned angular momentum and rotational frequency. Aligned quasiparticles influence the nuclear shape and subsequent alignments. Even-even $ ^{126-136} {\rm{Ba}}$ belong to a transitional region [9] where nuclear structure characteristics have been extensively studied using various models. The presence of two S-bands in this mass region is commonly attributed to the shape-driving effects of aligned $ h_{11/2} $ neutrons and protons acting on relatively soft nuclear cores [6]. Theoretical approaches, such as the microscopic models [9], the Interacting Boson Model (IBM) [10], and the General Collective Model (GCM) [11], have also been extensively used to study the low-energy spectrum in this region. The cranking approximation for the covariant density function theory was used to study the global dynamical correlation energies for the nuclei from $ Z = 8 $ to $ Z = 108 $ [12−16]. Recently, the cranking covariant density functional theory in a three-dimensional lattice space has been employed to investigate the octuple magic nucleus $ ^{144} {\rm{Ba}}$ [17]. Despite some experimental data and theoretical models addressing this phenomenon, a comprehensive and systematic study, especially regarding the stability and mechanisms of shape evolution at high spins, is still lacking. Therefore, it is necessary to adopt appropriate nuclear models to study both the ground state and high-spin shape evolution in Ba isotopes, to gain a deeper understanding of their structural properties.

In our previous work, we have investigated the evolution of ground-state quadrupole and octupole stiffnesses in even-even $ ^{112-150} {\rm{Ba}}$ using potential energy surface (PES) calculations [18]. We noticed that $ ^{118-128} {\rm{Ba}}$ has more stable quadrupole deformations and we have reproduced their experimental properties using the TRS calculationins [19]. In addition, $ ^{126-136} {\rm{Ba}}$ showed a dramatic increase with respect to the non-axial γ deformation in [18]. Based on these findings, it is meaningful to continue studying the shape evolution in these isotopes, particularly focusing on the stability of shape variations in high-spin states.

In this work, the nuclear shape evolution and rotational behavior along the yrast line in even-even $ ^{126-136} {\rm{Ba}}$ isotopes are investigated using TRS calculations in the ($ \beta_2, \gamma, \beta_4 $) deformation space. Our results reveal a transition from axially deformed shapes to non-axial configurations, with extreme γ-unstable shapes predicted for $ ^{130} {\rm{Ba}}$. The study also explores the evolution of the nuclear shape in high-spin states, showing a preference for non-collective oblate/triaxial shapes for $ \gamma > 0^\circ $ and collective oblate/triaxial shapes for $ \gamma < 0^\circ $.

The TRS calculation applied here is based on the pairing deformation self-consistent cranked shell model (CSM) [20−22]. This approach generally provides a reliable description of high-spin phenomena in rapidly rotating medium and heavy mass nuclei. The total Routhian, referred to as “Routhian” rather than “energy” in the rotating frame of reference, represents the sum of the energy of the ground state and the contribution from cranking.

The energy of the ground state is composed of a macroscopic component and a fluctuating microscopic component. The macroscopic part is derived from the standard liquid-drop model (LDM) with parameters established by Myers and Swiatecki [23]. The microscopic correction, arising from the non-uniform distribution of single-particle levels in the nucleus, mainly includes a shell correction and a pairing correction, calculated using the Strutinsky method [24] and the Lipkin-Nogami (LN) method [25], respectively. The Strutinsky smoothing procedure employs a sixth-order Laguerre polynomial with a smoothing range of $ 1.20\hbar\omega_0 $, where $ \hbar\omega_0 = 41/A^{1/3} $ MeV. The LN method is used to avoid the spurious pairing phase transitions encountered in simpler Bardeen-Cooper-Schrieffer (BCS) calculations. Both the shell and pairing corrections are evaluated based on a set of single-particle energy levels.

The single-particle energies required for the shell correction are obtained from the non-axially deformed Woods-Saxon (WS) potential, using a parameter set commonly employed in cranking calculations [26]. During the diagonalization of the WS Hamiltonian, oscillator basis states with principal quantum numbers $ N \leq 12 $ for protons and $ N \leq 14 $ for neutrons have been used. The nuclear shape is defined using the standard parametrization expanded in spherical harmonics [26]. The nuclear surface radius, $ R(\theta, \phi) $, extending from the origin to the surface of the nucleus, is described by the expression provided in [1].

$ R_{0} $ represents the radius at spherical equilibrium with the same volume $ R_{0} = r_0A^{1/3} $ and the function $ c(\hat{\beta}) $ ensures the conservation of the nuclear volume with a change in the nuclear shape and $ \hat{\beta} $ denotes the set of all the deformation parameters $ \alpha_{\lambda\mu} $ are the shape parameters. In general, a limiting value of $ \lambda < A^{1/3} $ can be obtained by a crude estimate [27]. The nuclear surface is described, for our purposes, by a second-order deformation [28].

In the present shape parametrization, we consider quadrupole and hexadecapole degrees of freedom, including nonaxial deformations, defined as $ \hat{\beta}\equiv (\alpha_{20},\alpha_{2\pm2}, \alpha_{40},\alpha_{4\pm2}, \alpha_{4\pm4}) $. Assuming the existence of three symmetry planes–($ x,y $), ($ y,z $) and ($ x,z $)– the number of independent coefficients α is reduced to five. These are expressed as

with $ \alpha_{20} $, and $ \alpha_{40} $, which can be expressed in terms of the standard $ (\beta_2,\gamma,\beta_4) $ parameters as

This leads to a three dimensional problem with the usual ($ \beta_2, \gamma, \beta_4 $) degrees of freedom. The quadrupole deformation parameter $ \beta_2 $ represents the magnitude of the deformation and the triaxiality parameter γ describes the deviation from axial symmetry.

Under the Lund convention [2], the Cartesian quadrupole coordinates were used to vary the quadrupole deformation in the calculations, including the γ degrees of freedom,

The γ parameter covers the range from $ -120^{\circ} $ to $ 60^{\circ} $. This range can generally be divided into three sectors: ($ -120^{\circ}<\gamma<-60^{\circ} $), ($ -60^{\circ}<\gamma<0^{\circ} $), and ($ 0^{\circ}<\gamma<60^{\circ} $), which represent the same triaxial shapes at the ground state but correspond to rotation about the long, medium, and short axes, respectively, at nonzero cranking frequency. The four limiting cases ($ \gamma = -120^{\circ}, -60^{\circ}, 0^{\circ} $, and $ 60^{\circ} $) correspond to the possible rotations of axially symmetric shapes: $ \gamma = -120^{\circ} $ and $ 0^{\circ} $ for prolate shapes, and $ \pm60^{\circ} $ for oblate shapes. These orientations describe different modes of rotation: $ \gamma = -120^{\circ} $ and $ 60^{\circ} $ indicate noncollective rotation around the symmetry axis, while $ \gamma = -60^{\circ} $ and $ 0^{\circ} $ correspond to collective rotation around an axis perpendicular to the symmetry axis.

Cranking constrains the nuclear system to rotate around a fixed axis (the x-axis) with a specified rotational frequency. Pairing correlations depend on both the rotational frequency and nuclear deformation. The resulting cranked-Lipkin-Nogami equation takes the form of the well-known Hartree-Fock-Bogolyubov-like (HFB) equation [22]. For a given rotational frequency and deformation point on the lattice, pairing correlations are treated self-consistently by solving this equation within a sufficiently large space of Woods-Saxon single-particle states.

The symmetries of the rotating potential can be used to simplify the cranking equations. In the reflection-symmetric case, both the signature quantum number r and the intrinsic parity π remain good quantum numbers. The solution characterized by $ (\pi, r) $ provides the energy eigenvalue, from which the energy relative to the non-rotating state can be directly obtained. After calculating the Routhians at fixed rotational frequencies, the values are interpolated using a cubic spline function between lattice points. The equilibrium deformation is then determined by minimizing the total Routhian surface (TRS).

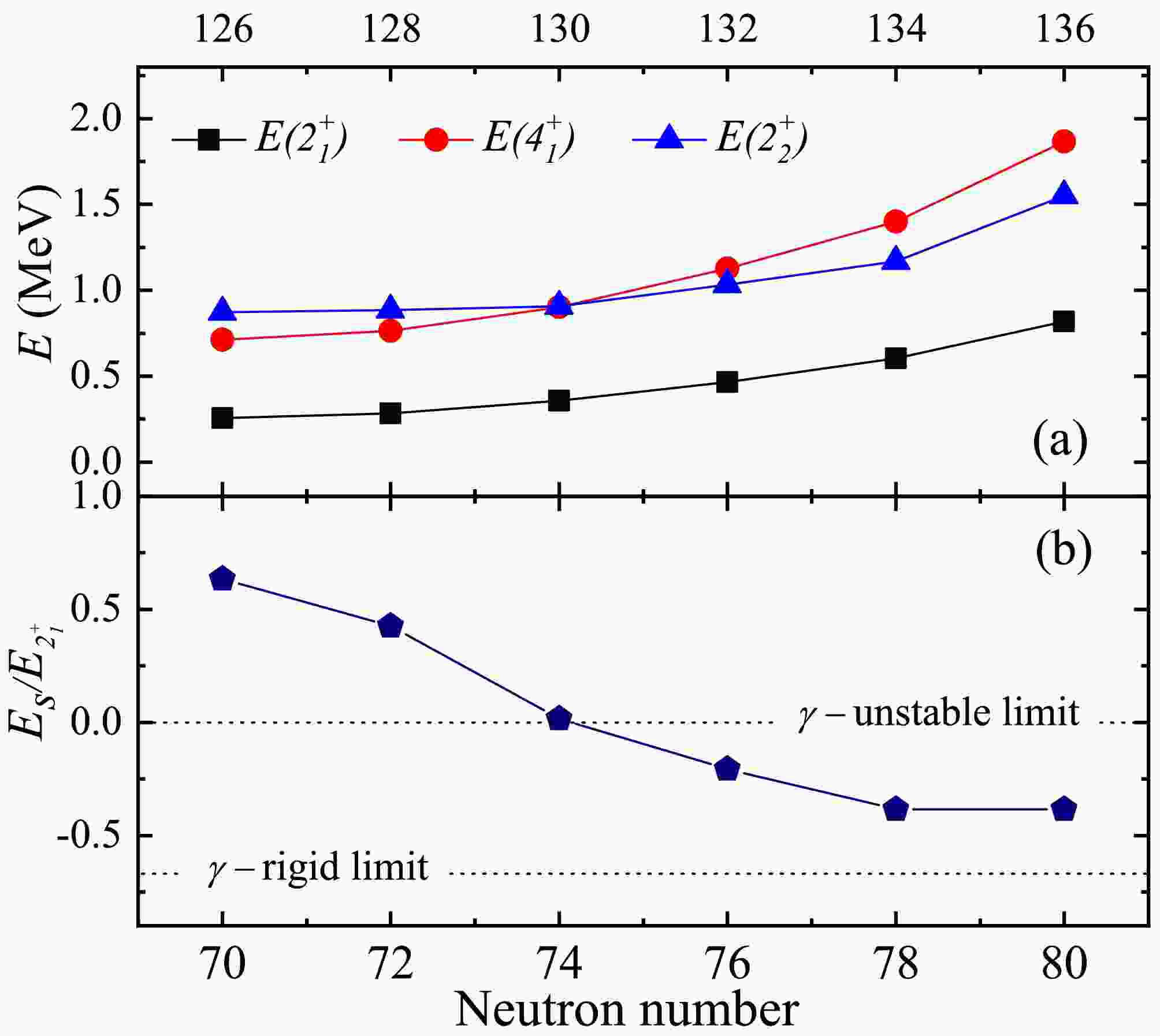
In nuclear structure research, phenomenological or empirical laws are often used as order parameters to reveal the shape phase evolution in nuclei [29]. Several such quantities and their evolution with neutron number are illustrated in Fig. 1. The energy of the first $ E(2_1^+) $ state serves as an indicator of quadrupole deformation $ \beta_2 $ in terms of the general empirical relation $ 6\hbar^2/2J = E(2_1^+)\approx 1225/A^{7/3}\beta_2^{2} $ MeV [30, 31]. As shown in Fig. 1 (a), the energy of the $ 2_1^+ $ state increases as the neutron number approaches the $ N = 82 $ closed shell, which indicates the decreasing of nuclear quadrupole deformation $ \beta_2 $ with neutron far from the close shell number. In addition to the $ E(2_1^+) $ states, the $ B(E2) $ transitions from the first $ 2^{+} $ to the ground state $ 0^{+} $ are a powerful tool for studying the nuclear deformations following the approximation: $ B(E2: 2^{+})\rightarrow 0^{+})\varpropto \beta^{2}_{2} $ [3]. As illustrated in Graph 28 of Ref. [32], the behavior of $ B(E2: 2^+) $ is inversely related to that of $ E(2_1^+) $, as shown in Fig. 1. As the number approaches shell closure, the $ B(E2: 2^+) $ transitions decrease, indicating a reduction of the prolate deformation.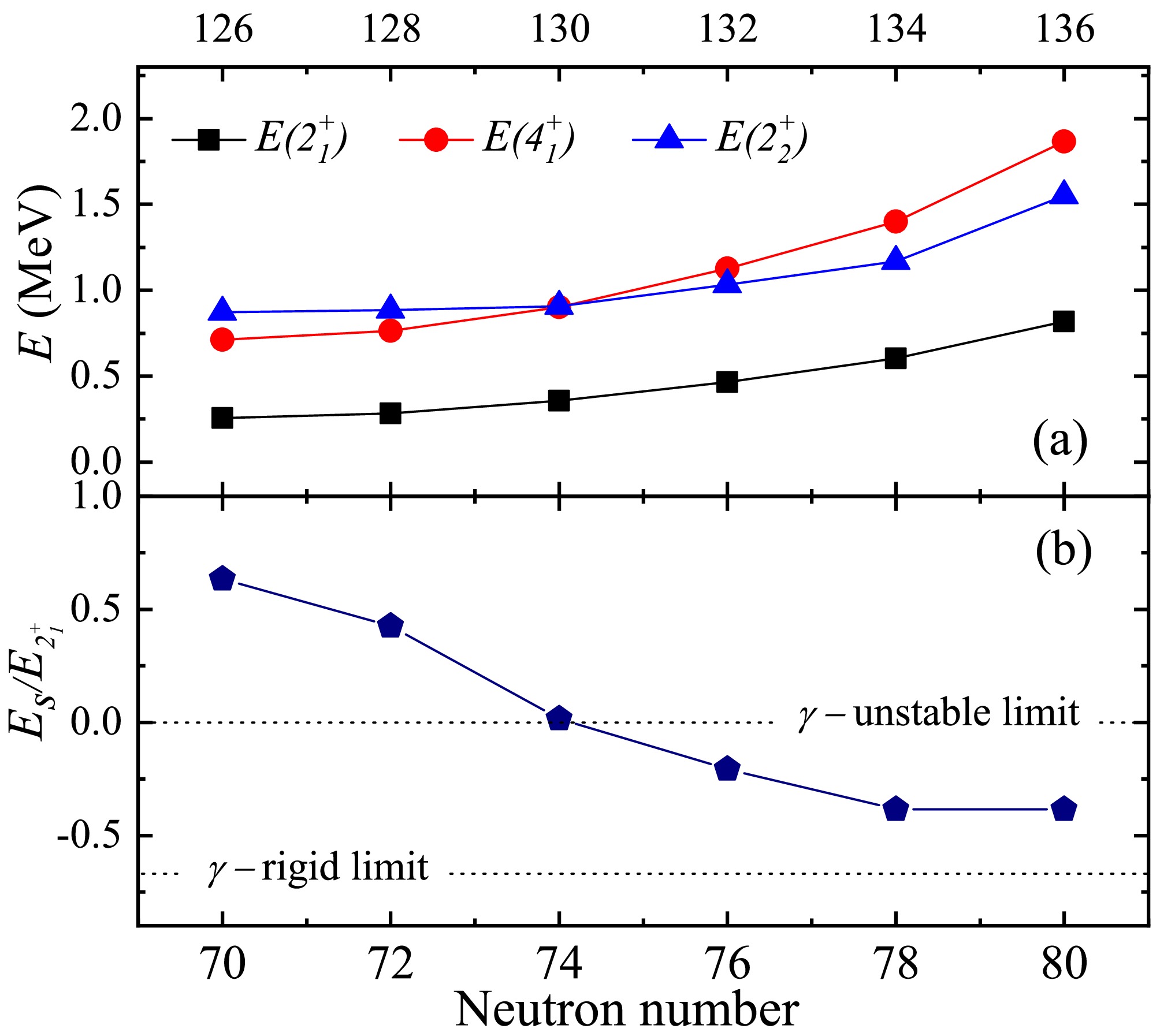

Figure 1.  (color online) (a) Energies of the first excited $2_1^+$, $4_1^+$, $2_2^+$ states, (b) Energy rario of $E_{S}/E_2^+$.

Deviation of the nuclear shape from axial symmetry can significantly influence the second-lowest $ 2_2^+ $ state, commonly associated with the quasi-γ bandhead in even-even nuclei. As shown in Fig. 1 (b), the systematic variation of the relative position of this $ 2_2^+ $ state with respect to the ground-state band can be clearly observed.

Empirically, the ratio $ E_s/E(2_1^+) $, where $ E_s = E(2_2^+) - E(4_1^+) $, plays the role of a global indicator of structural evolution associated with axial asymmetry [33]. In the extreme γ-unstable limit [34], the $ 2_2^+ $ and $ 4_1^+ $ states are completely degenerate, resulting in $ E_s/E(2_1^+) = 0 $, as observed in $ ^{130} {\rm{Ba}}$ nuclei [5]. Conversely, for a rigid triaxial rotor with $ 25^\circ \leq \gamma \leq 30^\circ $ [35], the $ 2_2^+ $ state lies below the $ 4_1^+ $ state, reaching a minimum value of $ E_s/E(2_1^+) = -0.67 $ at the extreme triaxiality of $ \gamma = 30^\circ $.

Nuclei with negative $ E_s/E(2_1^+) $ values between these two limits, $ 0 $ and $ -0.67 $, are typically characterized by γ-soft potential with shallow minimum around $ \gamma \approx 30^\circ $. In contrast, the positive value of $ E_s/E(2_1^+) $ observed in $ ^{126-128} {\rm{Ba}}$ suggests an axially symmetric shape, as their ground states are prolate and the $ 2_2^+ $ state lies at a relatively high excitation energy compared to the $ 2_1^+ $ and $ 4_1^+ $ states.

As shown in Fig. 1 (b), $ ^{132,134,136} {\rm{Ba}}$ exhibit negative values of approximately $ -0.20 $, $ -0.38 $, and $ -0.38 $, respectively, all higher than the rigid triaxial rotor limit of $ -0.67 $. The smallest ratio, around $ -0.38 $ in $ ^{134,136} {\rm{Ba}}$, remains slightly above the empirical value of $ E_s/E(2_1^+) \approx -0.5 $, which characterizes critical-point nuclei with maximal γ softness between prolate and oblate shapes.

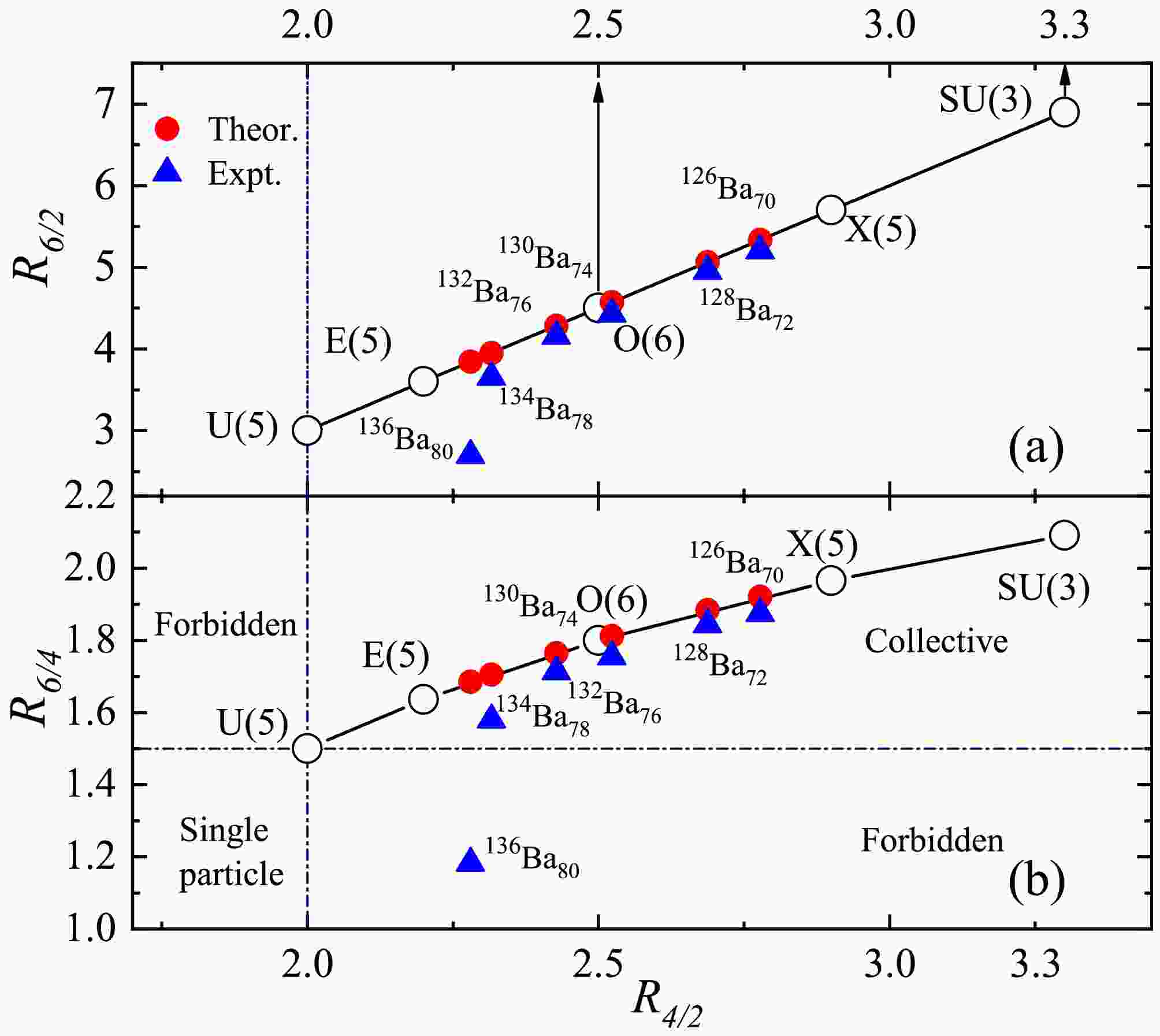
Nuclei in transitional regions often exhibit complex level structures and soft, non-rigid shapes. Direct measurement of certain quantities, such as the triaxial parameter γ, remains challenging. However, the energy ratio $ R_{4/2} \equiv E_{4_1^+}/E_{2_1^+} $ serves as a reliable indicator of nuclear shape deformation and can be used to assess the validity of the axial symmetry assumption. Deformations, including axially deformed, γ-unstable shapes, and spherical shapes, are all descriptions derived from collective models and serve to characterize different nuclear configurations.

For example, the energy ratio $ R_{4/2} $ is approximately $ 3.3 $ for a well-deformed axially symmetric rotor, $ 2.5 $ for a γ-unstable shape, and $ 2.0 $ for a spherical vibrator. These values correspond to the dynamical symmetry limit of SU(3), O(6), and U(5), respectively, in the IBM. More precisely, these symmetries represent different limiting cases: SU(3) for the axially deformed (axially symmetric) rotor, O(6) for the γ-unstable shape, and U(5) for the spherical vibrator. For the E(5) symmetry, which describes a critical point symmetry between the spherical vibrator and γ-unstable shape, the ratio is $ R_{4/2} \approx 2.2 $. For the X(5) symmetry, which is a critical point symmetry between the spherical vibrator and axially deformed states, it is approximately $ R_{4/2} \approx 2.9 $ [42, 43]. It was pointed out that the level energy ratios $ R_{I/2} $ are related to $ R_{4/2} $ [44]. Furthermore, a linear relation between $ R_{I/2} $ and $ R_{4/2} $ was established in [45] with

This relationship can be derived from the Mallmann plot [44], where $ R_{I/2} $ is plotted against $ R_{4/2} $. The linear relationship arises from the proportionality between certain quantities represented by the similar triangles in the plot. This relation is universal, applying to a range of nuclear shapes, including rotational, γ-unstable, and vibrational shapes, as well as the E(5) and X(5) symmetries.

As illustrated for even-even $ ^{126-136} {\rm{Ba}}$ in Fig. 2 (a), the linear relation between the energy ratio $ R_{6/2} $ and $ R_{4/2} $ is presented for the five typical shapes or symmetry limits, in comparing both the theoretical and experimental values. The theoretical ratio is given by $ R_{6/2} = 3R_{4/2}-3 $ as described in Eq. (5), while the experimental ratio is defined as $ R_{6/2} = E_{6^+}/E_{2^+} $. As shown in Fig. 2 (a), the ratio of even-even $ ^{126-132} {\rm{Ba}}$ follow a trajectory from vibrational towards an axially deformed shape, passing through an intermediate structure resembling γ-unstable shape, as noted in Ref. [46]. The calculated $ R_{6/2} $ value of these nuclei generally agrees well with the corresponding experimental results, particularly for $ ^{130} {\rm{Ba}}$, which is a typical example of the O(6) symmetry in the IBM, indicating the extreme γ-unstable limit, as shown in Fig. 1 (a).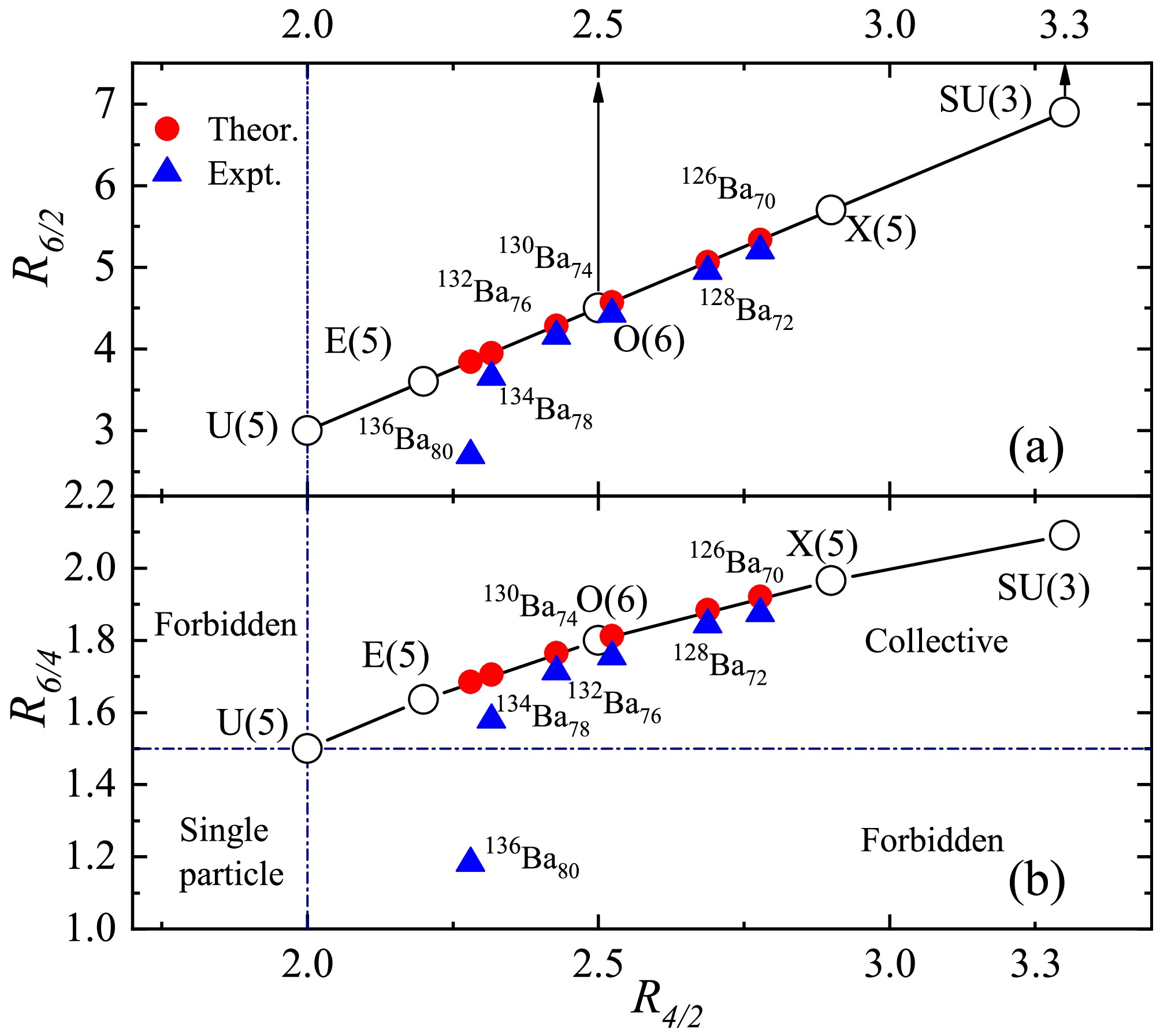

Figure 2.  (color online) (a) A linear plot of the energy ratio $R_{6/2}$ versus $R_{4/2}$ for the typical five symmetries (empty circles), together with the calculated (solid circles) and experimental values (solid triangles) for comparison. (b) Similar energy ratio to (a) but for $R_{6/4}$ versus $R_{4/2}$. “Theor.” represents theoretical values obtained using the empirical formula in Eq. (5), while the experimental data (“Expt.”) are taken from $^{126}{\rm{Ba}}$ [36], $^{128}{\rm{Ba}}$ [37], $^{130}{\rm{Ba}}$ [38], $^{132}{\rm{Ba}}$ [39], $^{134}{\rm{Ba}}$ [40] and $^{136}{\rm{Ba}}$ [41].

From the analytical perspective, the experimental energy ratio $ R_{6/2} $ for $ ^{134} {\rm{Ba}}$ is $ 3.66 $, closely matching the theoretical E(5) symmetry value of $ 3.95 $ with a deviation of approximately 7%. However, a more significant discrepancy between theoretical and experimental energy ratio exists for $ ^{136} {\rm{Ba}}$. Notably, Cizewski et al. pointed out [47] that the energy ratio $ R_{6/4} $ versus $ R_{4/2} $ provides a more universally applicable description across nearly all collective nuclei (see Fig. 2 (b)). The ratio $ R_{6/4} $ is less sensitive to variations in the moment of inertia, making it a more robust and less model-dependent parameter than $ R_{6/2} $, particularly in transitional regions.

In Reference [47], the onset of quadrupole collective motion is defined at $ R_{4/2} = 2.0 $, which corresponds to $ R_{6/4} = 1.5 $ in the collective model. Their plot of $ R_{6/4} $ versus $ R_{4/2} $ divides the parameter space into four regions: single-particle, collective, and two forbidden regions. Nuclei with $ R_{4/2} < 2.0 $ and $ R_{6/4} < 1.5 $ are characterized by single-particle excitations, while those with $ R_{4/2} \geq 2.0 $ and $ R_{6/4} \geq 1.5 $ correspond to collective excitations. The two forbidden regions, where $ R_{4/2} > 2.0 $ but $ R_{6/4} < 1.5 $, and $ R_{4/2} < 2.0 $ but $ R_{6/4} > 1.5 $, indicate conditions where the yrast structure does not align with either single-particle or collective excitation patterns.

As shown in Fig. 2 (b), the energy ratio $ R_{6/4} $ is plotted against $ R_{4/2} $, similar to Fig. 2 (a), with the calculated energy ratio given by $ R_{6/4} = 3 - 3/R_{4/2} $ and the experimental energy ratio by $ R_{6/4} = E_{6^+}/E_{4^+} $. For even-even $ ^{126-136} {\rm{Ba}}$, except for $ ^{136} {\rm{Ba}}$ ($ N = 80 $), the experimental energy ratio of $ R_{6/4} $ fall within the region where $ R_{4/2} \geq 2 $ and $ R_{6/4} \geq 1.5 $, which is the characteristic of collective excitations. As noted by Cizewski et al. in [47], several $ N = 80 $ nuclei, such as $ ^{136} {\rm{Ba}}$, exhibit energy ratio that fall into the forbidden region. The $ R_{4/2} $ value of these nuclei shown in Fig. 2 (b) is all greater than 2.0, suggesting a collective, possibly non-axial structure, while the $ R_{6/4} $ value point to a non-collective structure, typically associated with single-particle excitations. Since the yrast energy ratios are influenced by the coexistence of collective and non-collective excitations, a spherical vibrator mode may provide a more suitable description for these nuclei. This is particularly relevant for nuclei near closed shells, where low-energy excitations are primarily governed by the motion of a few valence nucleons within spherical shell model orbitals. In contrast, as one moves away from shell closure, quadrupole collective excitations—ranging from vibrations near shell closure to rotations in mid-shell—become dominant. For isotopes $ ^{134-136} {\rm{Ba}}$ near the $ N = 82 $ shell, their relatively spherical shape suggests that their excitations can be understood as a coupling between single-particle states and collective vibrational motion.

It is shown in Figs. 1-2 that, as the neutron number increases from $ N = 70 $ to $ N = 80 $, the collective characteristic linked to quadrupole deformation gradually diminish. Specifically, it is shown that $ ^{130} {\rm{Ba}}$ lies at the γ-unstable point, while $ ^{136} {\rm{Ba}}$ exhibits a non-collective structure. Since nuclear rotational properties are shaped by the deformation and configuration of the ground state, it is intriguing to explore the shapes that emerge from soft, γ-unstable, and non-collective configurations.

The above conclusions are based on phenomenological and empirical laws that describe nuclear deformation and low-energy states. To gain deeper insight into the microscopic mechanisms underlying these phenomena, we employ the TRS approach. This method allows us to not only compare TRS results with previous experimental data based on collective models and the IBM but also to uncover the microscopic origins of these experimental observations. By comparing the TRS calculations with experimental findings, we can validate and refine predictions from collective models and the IBM, ultimately advancing a more comprehensive understanding of nuclear structure. In the next section, we present result of the TRS calculations and its integration with experimental data and other theoretical frameworks, providing a more precise perspective on nuclear deformation and structural characteristics.

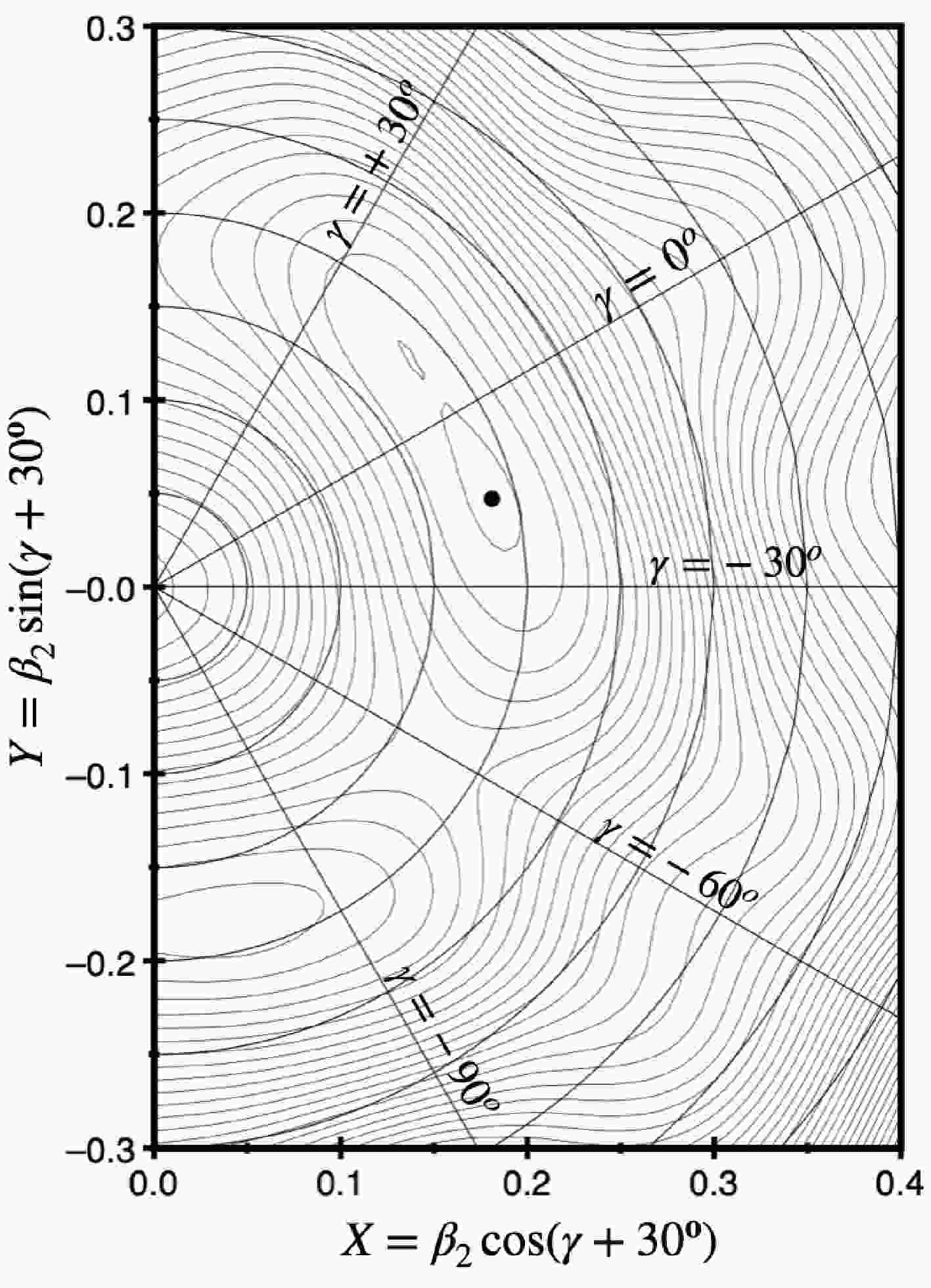
Within the framework of TRS calculations, the equilibrium deformation denoted by the black dot can be extracted from the potential energy surface. As illustrated in the example of $ ^{130} {\rm{Ba}}$ presented in Fig. 3, the equilibrium deformation at the ground state is around $ \beta_2 = 0.184 $, $ \gamma = -10.5^{\circ} $ $ \beta_4 = -0.006 $. The non-zero γ deformation indicates the flexibility of the shape in $ ^{130} {\rm{Ba}}$, which agrees with the empirical prediction of the γ-unstable shown in Fig. 1. Since this nucleus is soft, the deformations and shapes may change easily. As known that the dependence of the deformations can be studied by the single-particle level diagram qualitatively. In Fig. 4, we present the Single-particle energy levels as functions of quadrupole deformation $ \beta_2 $ and non-axil deformation γ.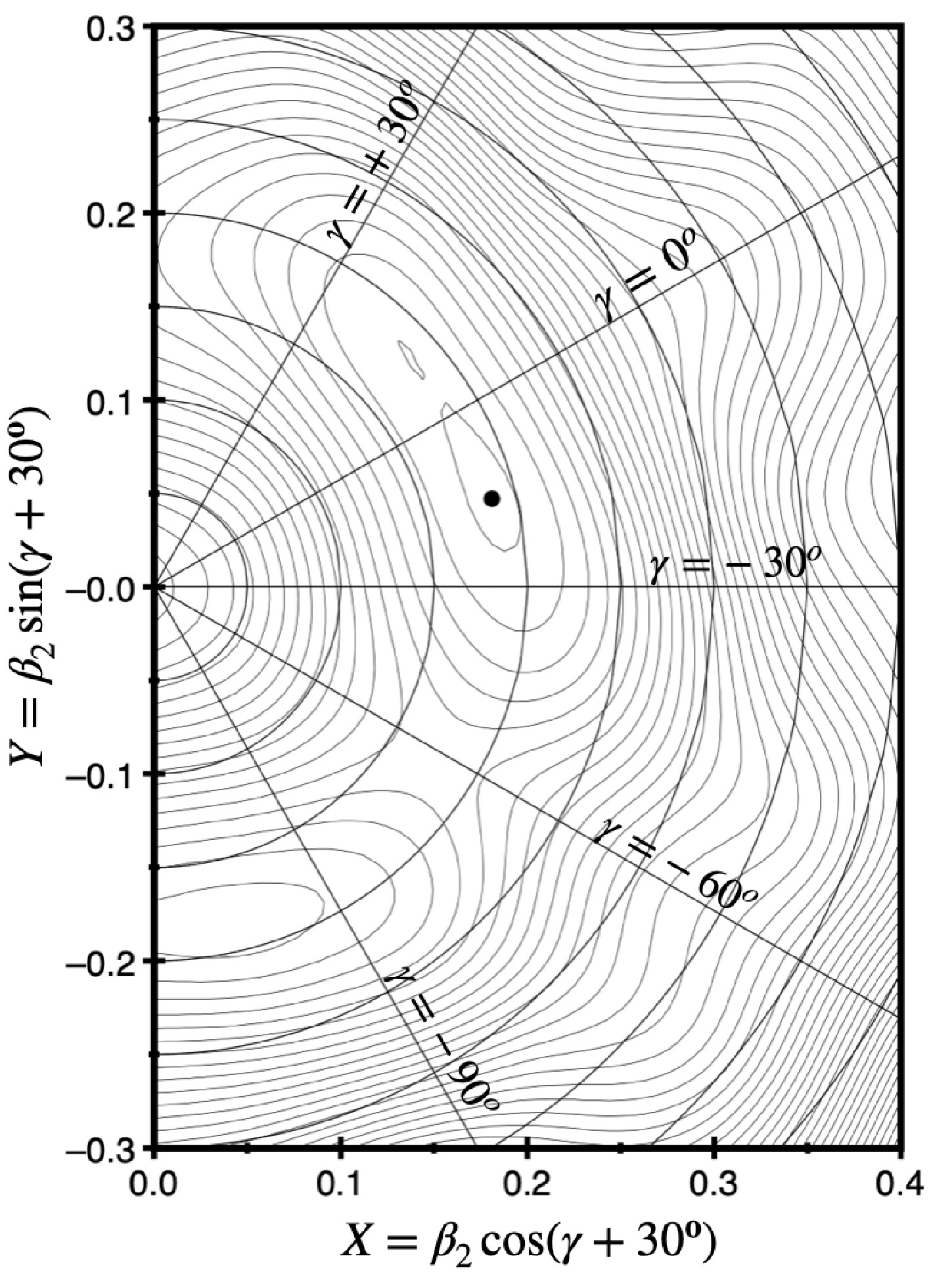

Figure 3.  (color online) Example of the potential energy surface projected on the Cartesian quadrupole coordinates for $^{130}{\rm{Ba}}$. The equilibrium deformation denoted by the black point is obtained by minimizing the TRS. Quadrupole deformation $\beta_2$ can be read from the circles and the typical γ deformations representing the prolate shape ($\gamma = 0^{\circ}$ and $\gamma = -120^{\circ}$), triaxial shape ($\gamma = \pm30^{\circ}$), and oblate shape ($\gamma = \pm60^{\circ}$) are marked.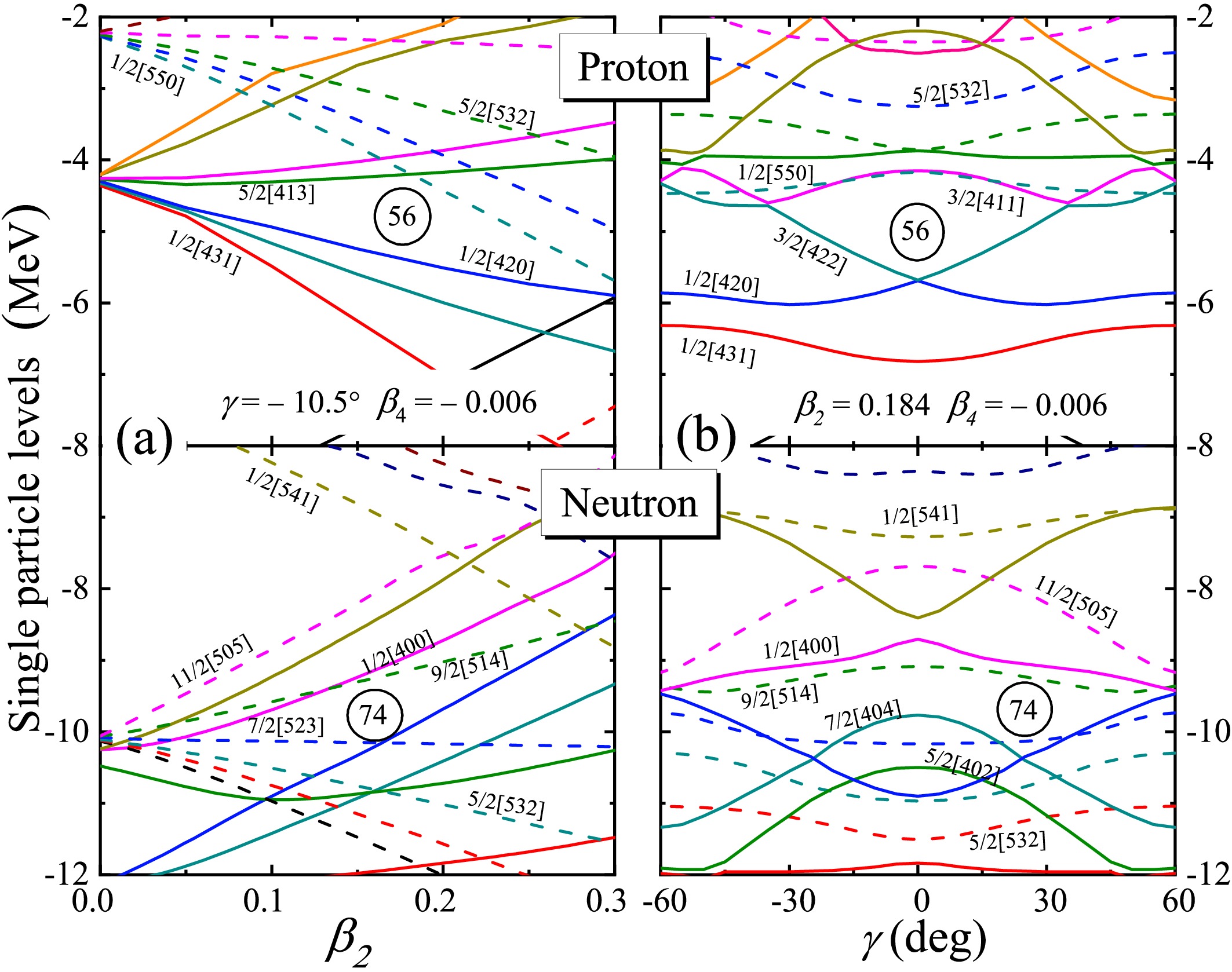

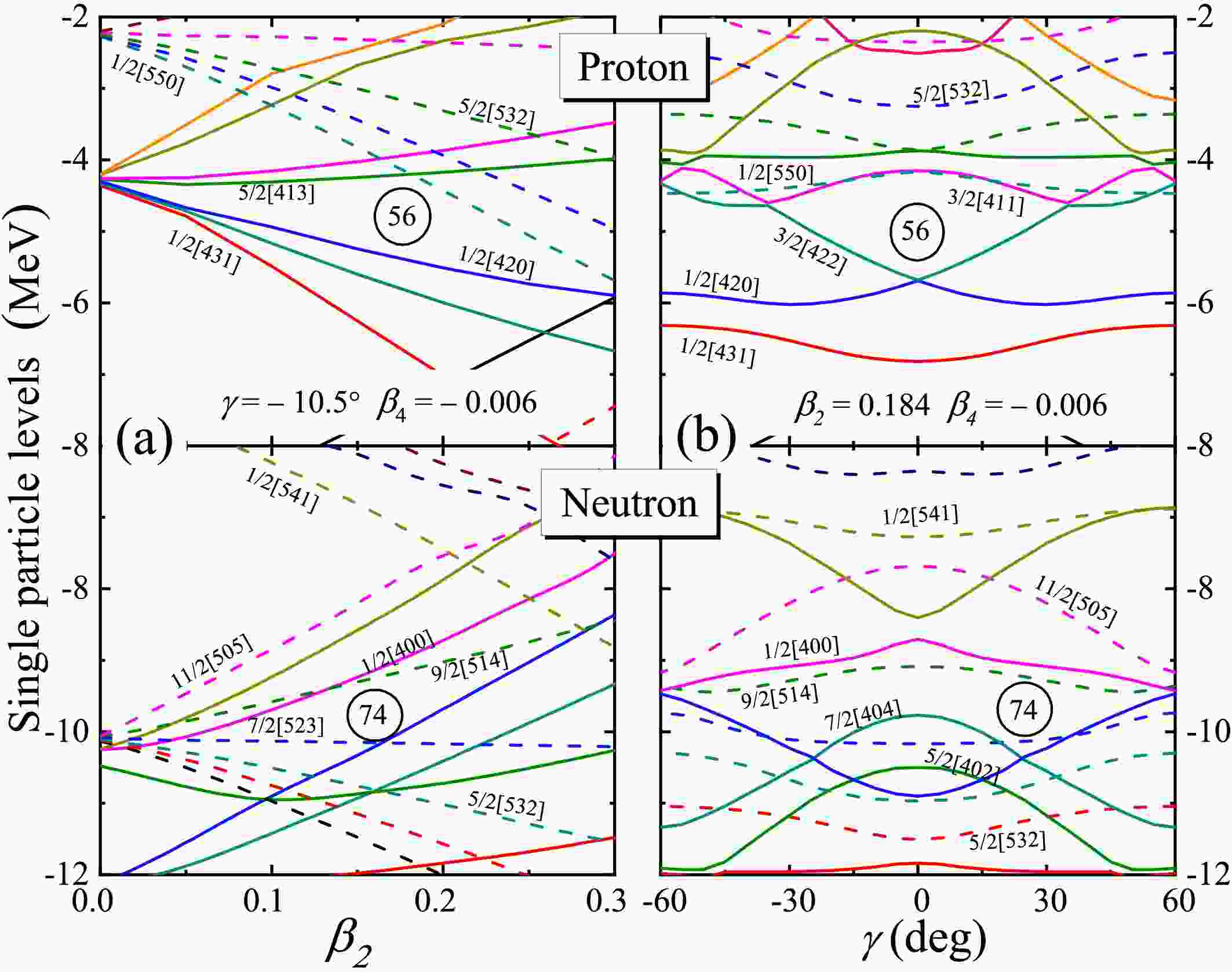
Figure 4.  (color online) (a) Single-particle levels calculated with a Woods-Saxon potential for $^{130}{\rm{Ba}}$ as a function of $\beta_2$ of proton (upper) and neutron (lower) at $\gamma = -10.5^{\circ}$ and $\beta_4 = -0.006$. The solid and dashed lines denoted the positive and negative parity levels and marked with the asymptotic labels $[Nn_z\Lambda]\Omega$. (b) Similar to (a), the single-particle levels as a function of γ of proton (upper) and neutron (lower) for ground state $\beta_2 = 0.184$ and $\beta_4 = -0.006$.

Notably, in Fig. 4 (a), there are some differences compared to the standard modified harmonic oscillator Nilsson diagram (see Ref. [48]), which can be attributed to the virtual crossings being preserved and the considerable γ deformation. The proton Fermi surface of $ Z = 56 $ lies in the lower part of the $ h_{11/2} $ orbitals, favoring an elongate shape. In contrast, neutrons $ N = 74 $ gap appears at $ \gamma\approx\pm15^{\circ} $ which indicates the γ-soft deformation and it agrees with the empirical result of γ-unstale of $ ^{130} {\rm{Ba}}$ as shown in Fig. 1 and Fig. 2. Additionally, occupying medium- to high-Ω orbitals of the $ h_{11/2} $ subshell, which can lead to significant γ deformation or oblate deformation at $ \gamma = \pm60^{\circ} $. It exhibits a strong dependence on γ deformation compared to the lower-Ω orbitals. This behavior aligns with the well-established deformation-driving properties of spin-aligned unique parity orbitals [6, 49]. When the Fermi surface is near the bottom of the shell, prolate shapes or shapes with positive γ values are energetically favored. As the Fermi surface moves upward through the shell, collective triaxial deformation becomes prominent, and ultimately, near the top of the shell, an oblate shape is preferred.

In rapidly rotating nuclei, the Coriolis and centrifugal interactions can become sufficiently strong to alter nucleonic motion and disrupt superfluid (pairing) correlations and nuclear shape (mean-field).

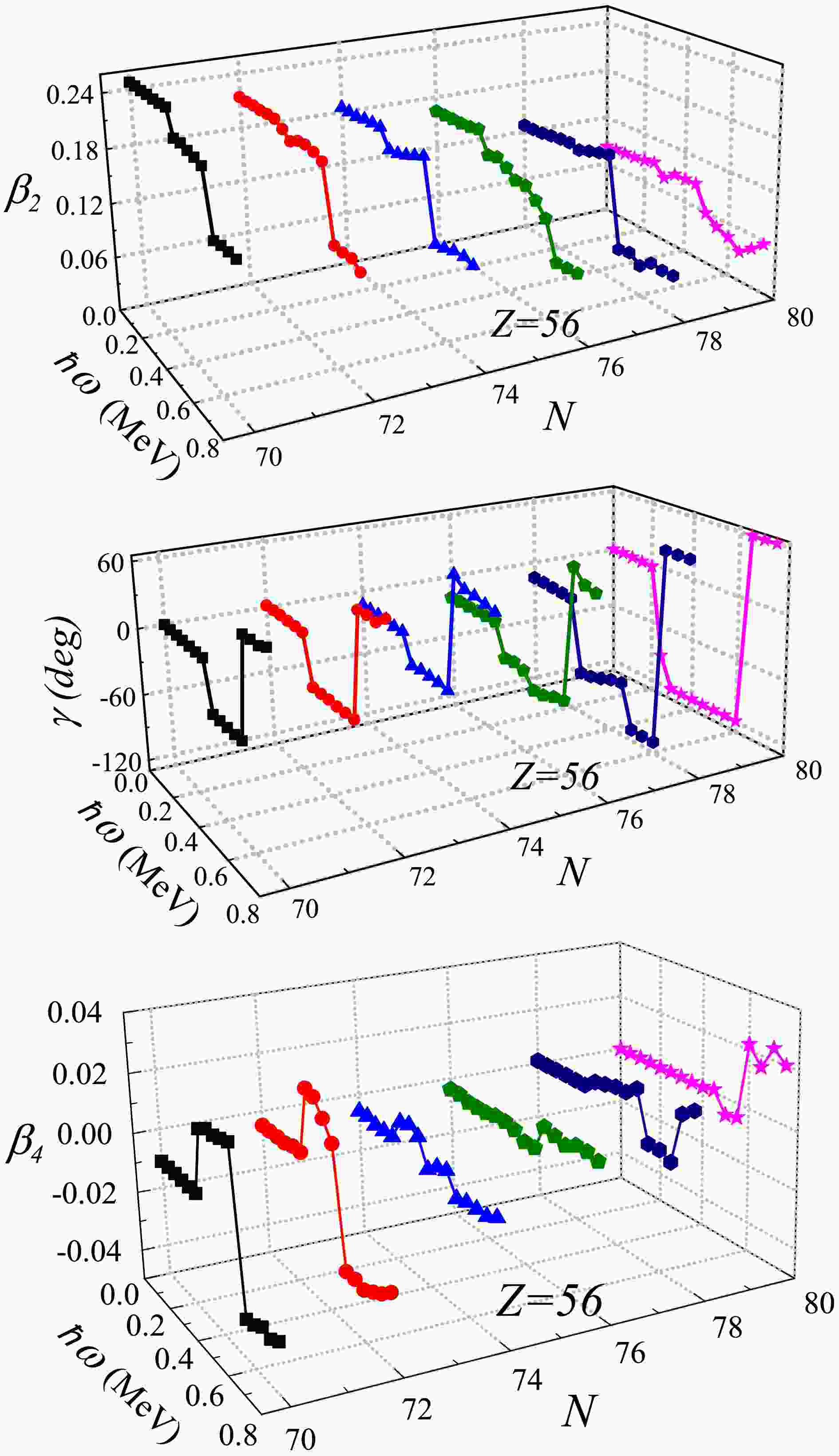
Figure 5 illustrates the evolution of the axial $ \beta_2 $ deformation, non-axial γ deformation and hexadecapole $ \beta_4 $ deformation for even-even $ ^{126-136} {\rm{Ba}}$ isotopes. The well deformed prolate shapes with ($ \beta_{2}\approx0.25, \gamma\approx0.0, \beta_4\approx-0.011 $) and ($ \beta_{2}\approx0.22, \gamma\approx0.0, \beta_4\approx-0.006 $) are presented in $ ^{126,128} {\rm{Ba}}$, whcih corresponds to the results in [36, 37]. The significant triaxial deformations shown in Figure 5 (middle) are predicted for the ground states of $ ^{130-134} {\rm{Ba}}$ isotopes [38−41, 50, 51]. The ground state deformations ($ \beta_{2}, \gamma,\beta_4 $) at $ \hbar\omega = 0 $ reveal systematic trends with increasing neutron number, consistent with experimental data shown in Fig. 1, and reflect the interplay between shell effects and deformation-driving interactions. The transitions in shape from prolate to γ-soft and then to spherical in isotopes $ ^{126-136} {\rm{Ba}}$ are consistent with the microscopic analysis performed using self-consistent relativistic mean-field theory combined with BCS calculations, as reported in Ref. [52]. Unstable γ deformations observed in isotopes $ ^{132} {\rm{Ba}}$ and $ ^{134} {\rm{Ba}}$ have been recognized as potential candidates for $ E(5) $ behavior according to the self-consistent Hartree-Fock-Bogoliubov approximation [53] and the $ ^{134} {\rm{Ba}}$ has been studied as the promising candidate Ref. [52], as well as by the self-consistent Relativistic Hartree Bogoliubov formalism in Ref. [54].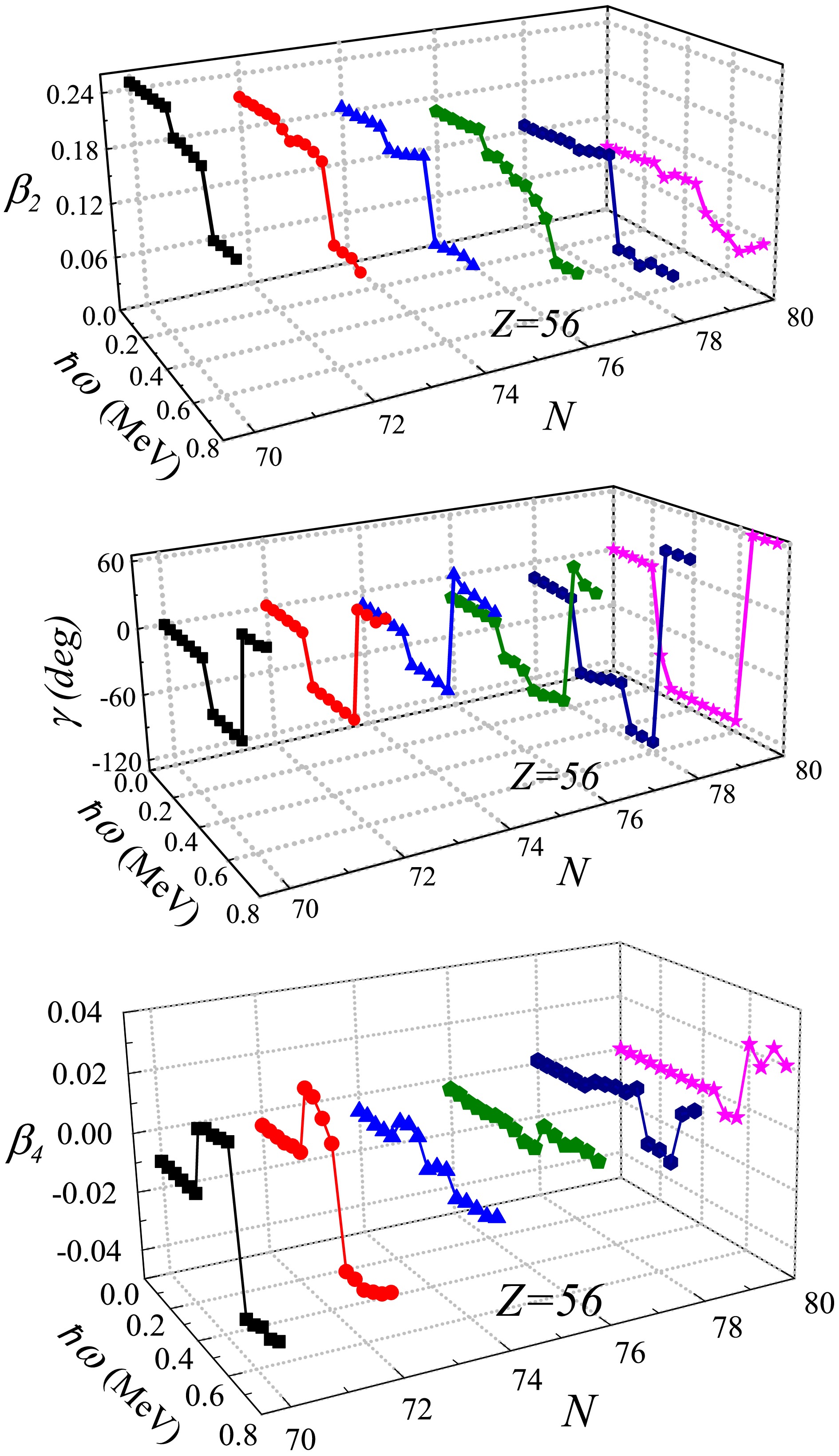

Figure 5.  (color online) Calculated deformation parameters $\beta_2$ (top), γ (middle) and $\beta_4$ (bottom) of yrast states for even-even $^{126-136}{\rm{Ba}}$ isotopes as a function of the rotational frequency $\hbar\omega$.

Recently, the impact of hexadecapole deformation has garnered attention in nuclear studies due to its association with enhanced electric hexadecapole transitions and the low-energy $ k^{\pi} = 4^{+} $ band cf. Ref. [55]. As illustrated in Fig. 5, the transition of hexadecapole $ \beta_4 $ deformations from negative to positive values corresponds to a change in shape from more prolate to more oblate, which agrees with the calculations presented in Refs. [49, 56].

The results shown in Fig. 4 and Fig. 5 demonstrate the feasibility and effectiveness of the TRS approach in describing the shape evolution of atomic nuclei. The consistency between the TRS calculations and empirical observations in Fig. 1 and Fig. 2 confirms that the model can reliably capture both axial and triaxial deformation features across the Ba isotopic chain. The evolution of single-particle energy levels emphasizes the essential role of proton and neutron Fermi configurations in determining the preference for prolate, triaxial, or oblate shapes. The calculated deformation parameters ($ \beta_{2}, \gamma $, $ \beta_4 $) reveal systematic trends with increasing neutron number, consistent with experimental data, and reflect the interplay between shell effects and deformation-driving forces. Therefore, the TRS approach not only proves effective in describing nuclear shape evolution but also provides a possible microscopic foundation under this model for the phenomena observed through phenomenological and empirical laws in Fig. 1 and Fig. 2.

The equilibrium deformation is determined by minimizing the total Routhian surface at each rotational frequency, as illustrated in Fig. 3. With changes in the rotation frequency, the locations of the equilibrium deformations displayed on the potential energy surfaces in Fig. 3 may also shift. In Fig. 6, we present a schematic illustration of the positions of the energy minima on the potential energy surface (PES) in the TRS for even-even $ ^{126-136} {\rm{Ba}}$ isotopes, with rotational frequency increasing from $ 0.0 $ to $ 0.80 $ MeV. The circles in the figure represent the positions of the energy minima corresponding to different values of rotational frequency. Each red circle in Fig. 6 represents an energy minimum, corresponding to the black dot in Fig. 3, indicating the equilibrium deformation at different rotational frequencies.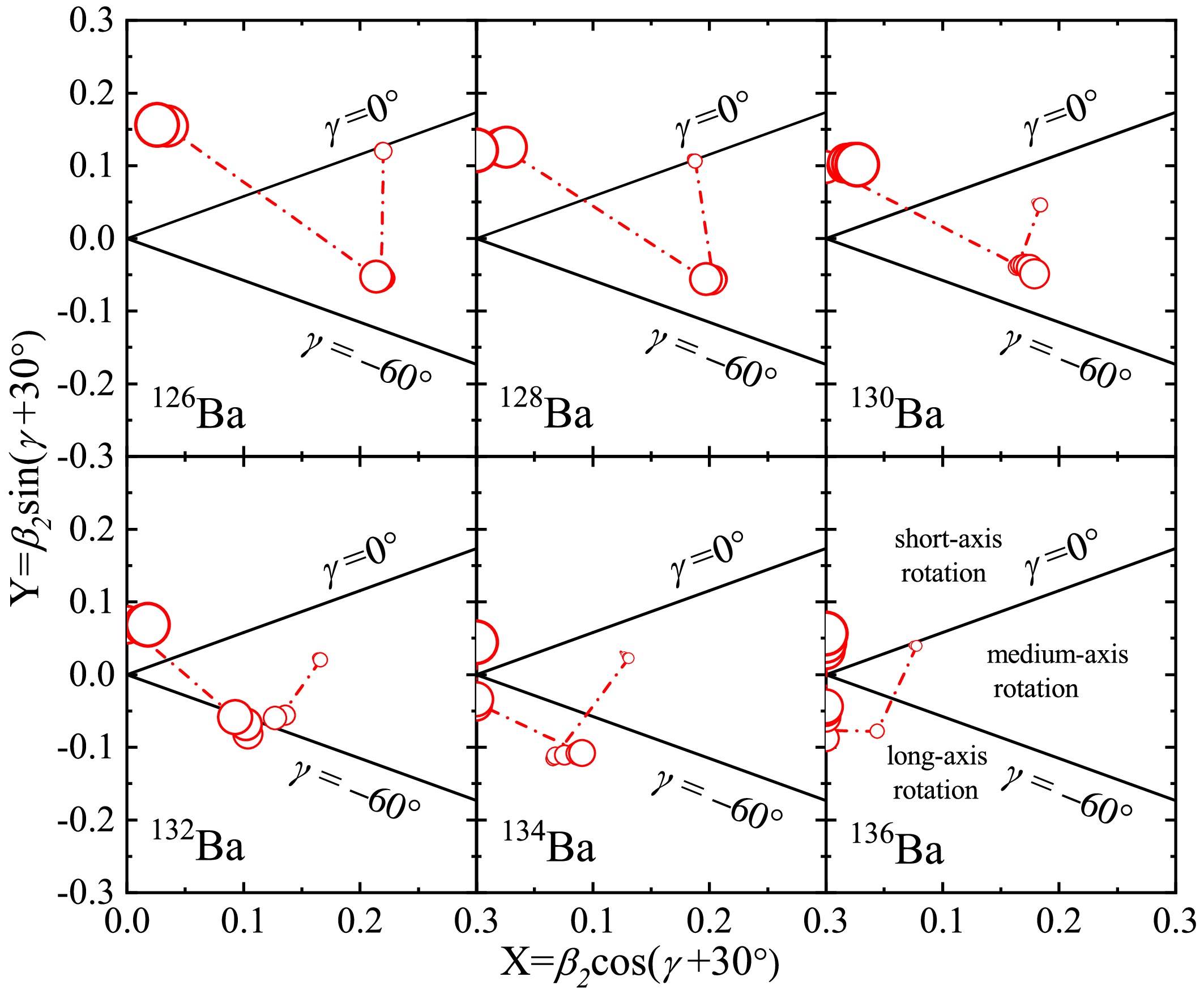

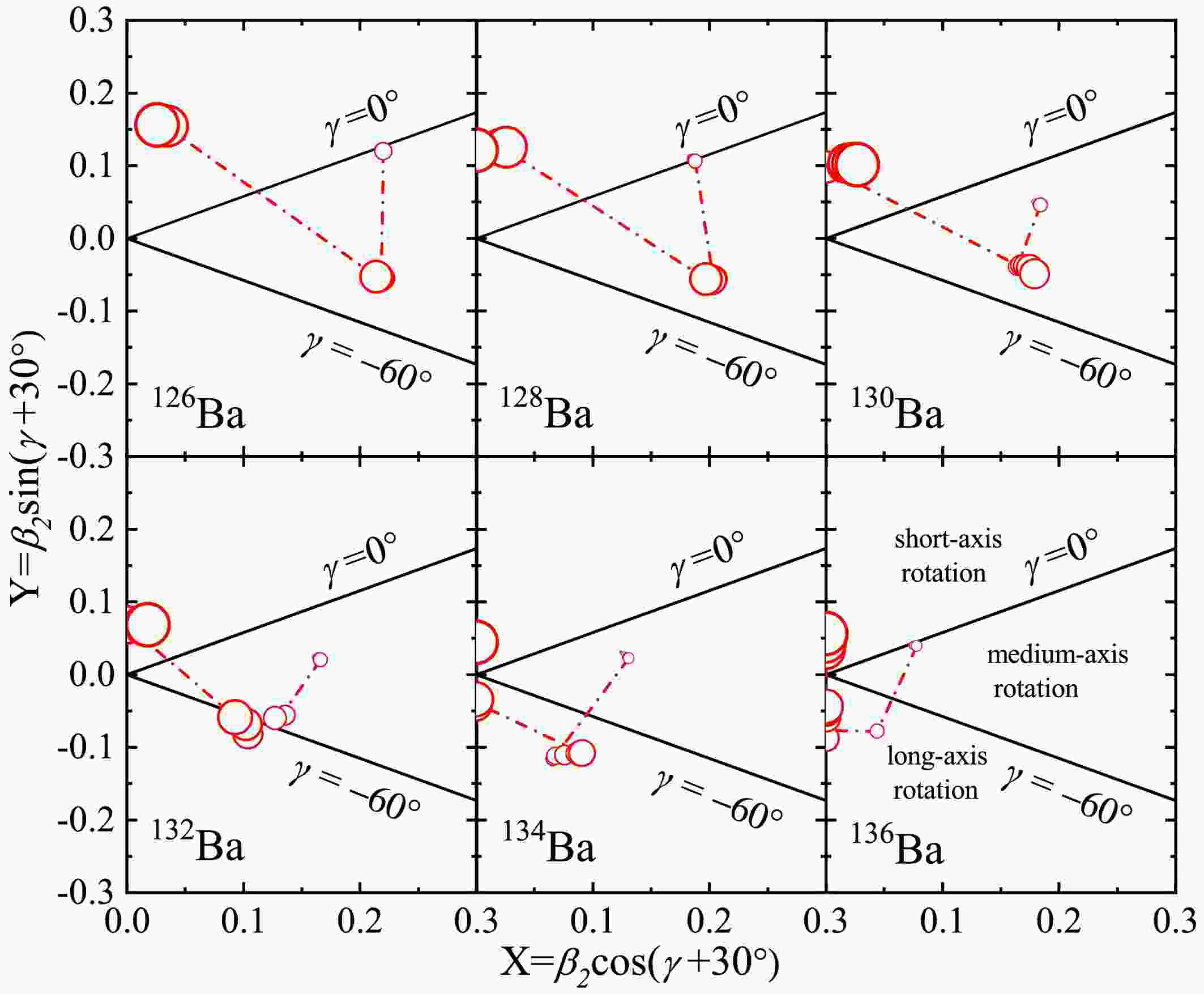
Figure 6.  (color online) Schematical illustration of the positions of the energy minima in the TRS for even-even $^{126-136}{\rm{Ba}}$ isotopes, the gradually increasing circles represent the rotational frequency $\hbar\omega$ increased from 0.00 to 0.80 MeV, the γ range can be divided into three sectors $(-120^{\circ}$, $-60^{\circ})$, $(-60^{\circ}$, $0^{\circ})$, and $(0^{\circ}$, $60^{\circ})$, which respectively represent rotation about the long, medium, and short axes, respectively.

As the rotational frequency increases, the positions of these minima shift, indicating the evolution of the nuclear shape and deformation. To visually capture this evolution, we created the schematic diagram in Fig. 6, where the varying sizes of the circles represent the changes in the minima locations as frequency increases. In the case of even-even $ ^{126-130} {\rm{Ba}}$ isotopes, the rotational axis evolves from intermediate-axis rotation ($ -60^\circ < \gamma < 0^\circ $) to short-axis rotation ($ 0^\circ < \gamma < 60^\circ $) with increasing rotational frequency. For the even-even $ ^{132-136} {\rm{Ba}}$ isotopes, the transition starts with intermediate-axis rotation and moves towards long-axis rotation ($ -120^\circ < \gamma < -60^\circ $), ultimately shifting towards short-axis rotation as the frequency increases.

To explore the evolution of nuclear shape and the corresponding rotational axes, we present the calculated collective angular momenta for the even-even $ ^{126-136} {\rm{Ba}}$ nuclei in Fig. 7, including both proton and neutron components. As discussed previously, the even-even $ ^{126-136} {\rm{Ba}}$ nuclei exhibit a rotational axis transition from an intermediate-axis, through a long-axis, to a short-axis rotation with increasing rotational frequency.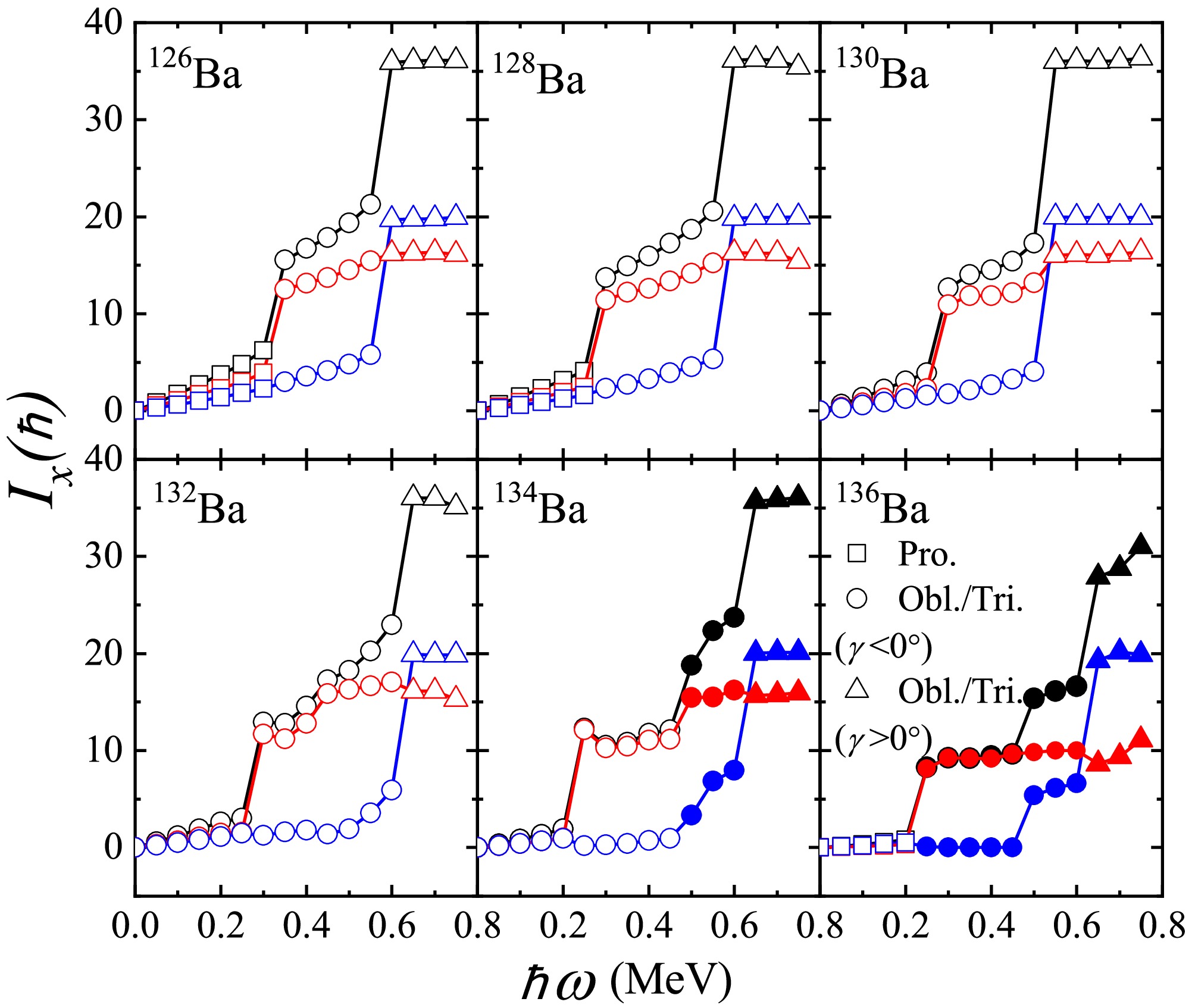

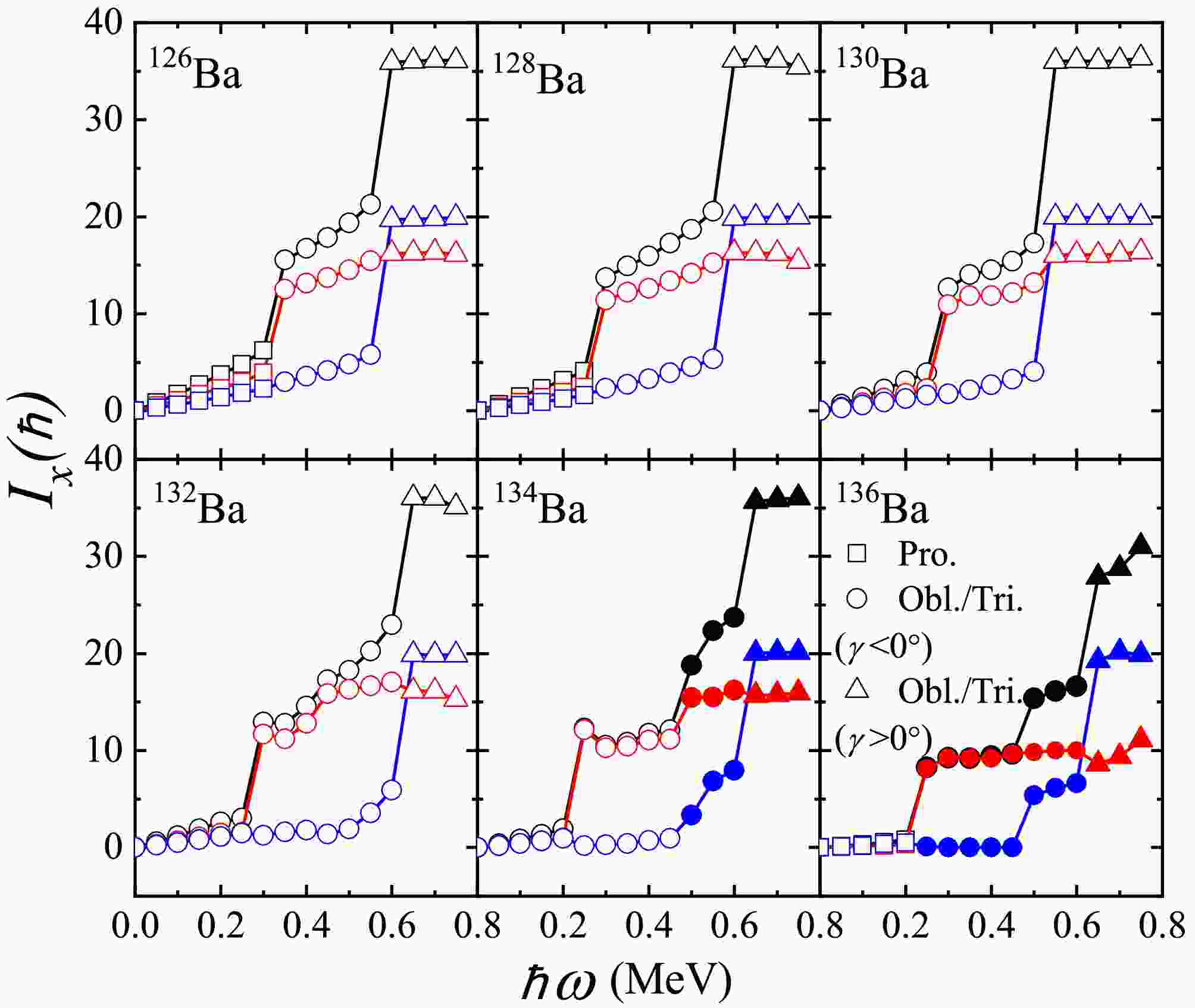
Figure 7.  (color online) Calculated aligned angular momentum (black symbols) against rotational frequency $\hbar\omega$ for even-even $^{126-136}{\rm{Ba}}$ isotopes, together with the proton (blue symbols) and neutron (red symbols) components. The squares, circles and triangles represent prolate(Pro.), oblate/triaxial (Obl./Tri.) ($\gamma<0^{\circ}$) and oblate/triaxial ($\gamma>0^{\circ}$) (the solid symbols denote non-collective mode), respectively.

The first substantial increase in total aligned angular momentum can be attributed to the neutron contribution. The rotational alignment of a pair of $ h_{11/2} $ neutrons at $ \hbar\omega\sim 0.3 $ MeV is evident due to the significant gain of approximately $ 10 \hbar $. A second increase in rotational alignment appears to occur at a higher frequency, around $ \hbar\omega\sim 0.5 $ MeV, where proton alignment becomes more favorable. This leads to distinct differences in the shape and rotational axis driving tendencies between protons and neutrons. The proton and neutron $ h_{11/2} $ configurations favor shapes with $ \gamma > 0^{\circ} $ (non-collective oblate/traxial) and $ \gamma < 0^{\circ} $ (collective oblate/triaxial), respectively [36−39, 50, 57].

Therefore, the alignments are seen to depend sensitively on the nuclear shape and rotational axis. The significant nuclear shape change associated with the alignment of the $ (\nu h_{11/2})^2 $ configuration may explain why the $ 10^+ $ bandhead of this two-quasineutron configuration is found to be isomeric, with measured mean lifetimes of $ \tau = 12.5\pm0.3 $ ns in $ ^{132} {\rm{Ba}}$ [50] and $ 91\pm2 $ ns in $ ^{136} {\rm{Ba}}$ [41].

High-j nucleons occupying orbitals close to the Fermi surface are strongly influenced by the Coriolis interaction, which tends to align single-particle angular momenta along the rotation axis [58]. The $ ^{136} {\rm{Ba}}$ nucleus lies near the neutron shell closure ($ N = 82 $) and in the proton mid-shell between the $ Z = 50 $ and $ 64 $ shell closures. In this region, an interplay between quadrupole collectivity and single-particle degrees of freedom can exist even in relatively low-lying states [57]. The $ \nu(h_{11/2})^2 $ configuration is expected to be dominant in the $ ^{134,136} {\rm{Ba}}$ isotopes [57, 59], where the first neutron alignment drives the nuclear shape from triaxial/oblate towards non-collective prolate ($ \gamma = -120^{\circ} $) or non-collecitve oblate ($ \gamma = +60^{\circ} $). This evolution corresponds to the non-collective configuration predicted by the empirical laws shown in Fig. 2, while the TRS calculations provide a clear representation of the collective and non-collection shape characterized by different γ values, see Fig. 6.

The quasiparticle driving interaction competes with the core's restoring interaction, which favors $ \gamma = 0 $ at $ \hbar\omega = 0 $. As ω increases, progressively negative γ values become energetically preferred due to the irrotational flow behavior of collective rotation [60].

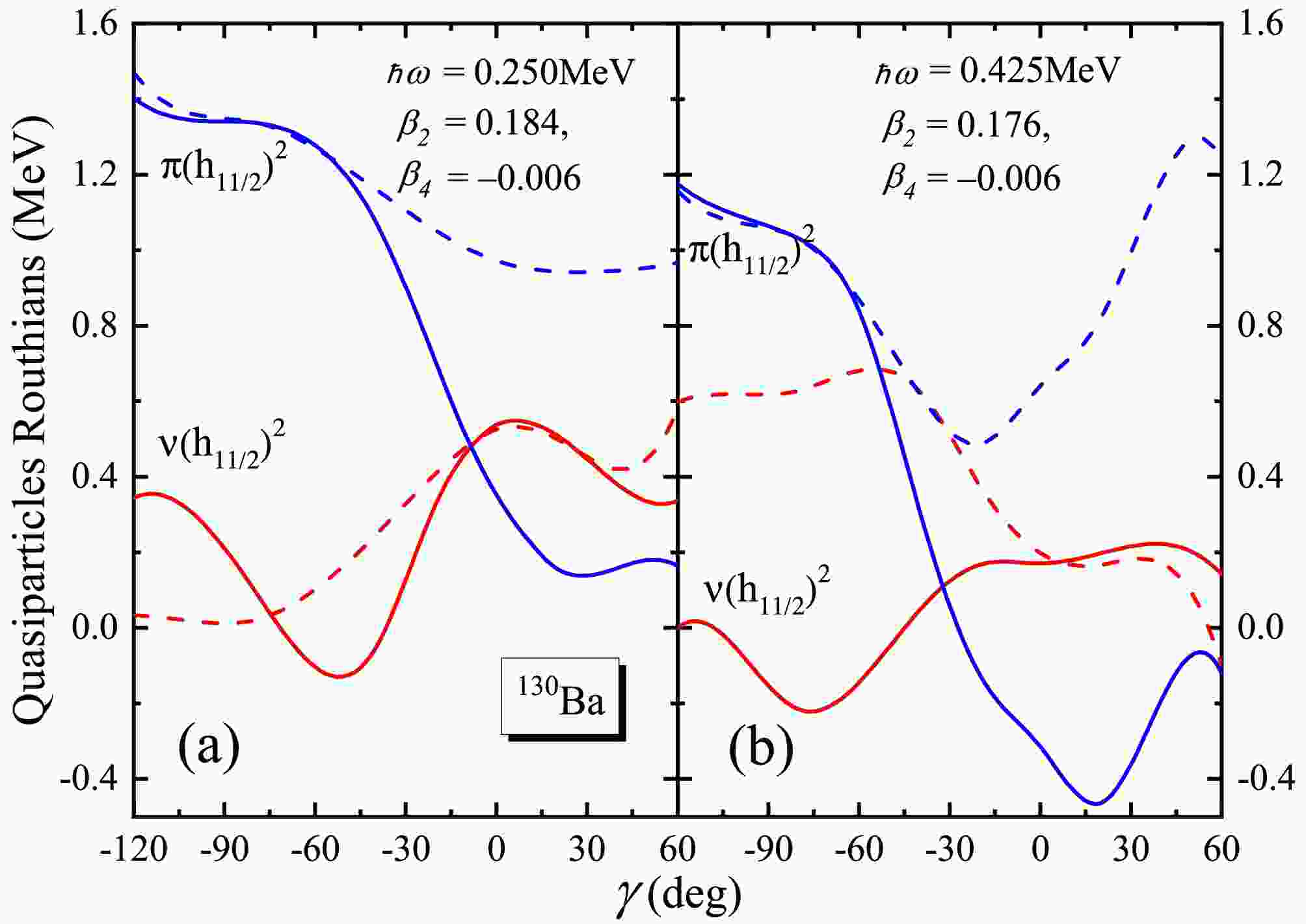
The shape-driving interactions (proportional to the slope in Fig. 8), are exerted by the quasiparticles, particularly the two-quasiproton and two-quasineutron configurations in the $ h_{11/2} $ orbital. As shown in Fig. 8, the $ (\nu h_{11/2})^2 $ quasineutron configuration influences the evolution of the shape more strongly than the $ (\pi h_{11/2})^2 $ quasiproton configuration near the first rotational alignment frequency, as depicted in Fig. 8(a). Consequently, γ values tend to cluster around $ \gamma \sim -40^\circ $, where oblate and triaxial shapes with negative γ dominate, as shown in Fig. 7.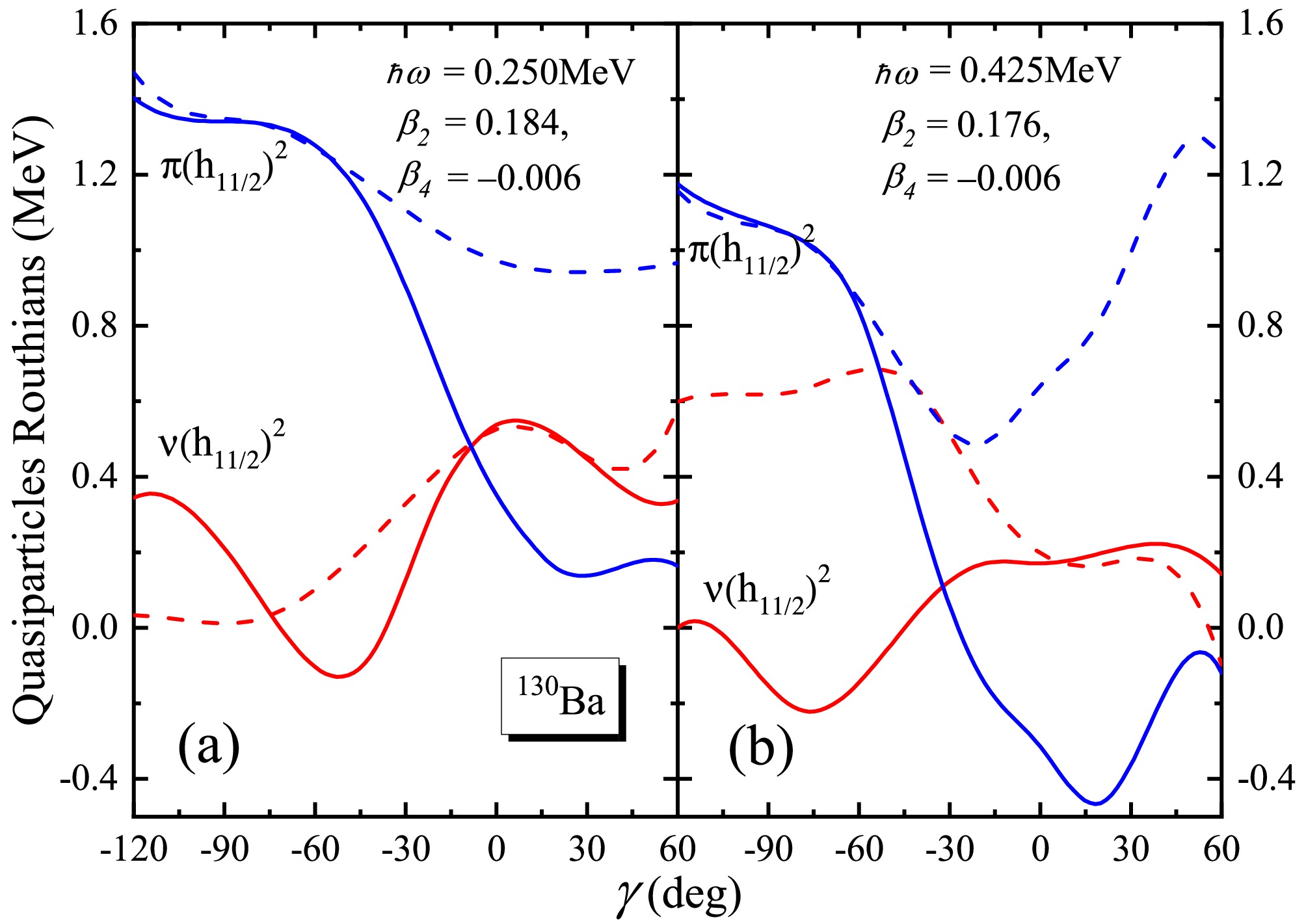

Figure 8.  (color online) (a) Calculated $(\pi h_{11/2})^2$ and $(\nu h_{11/2})^2$ quasiparticles Routhians as functions of triaxial deformation γ for $^{130}{\rm{Ba}}$ at a given frequency (close to the first rotational alignment frequency) $\hbar\omega = 0.250$, $\beta_2 = 0.184$ and $\beta_4 = -0.006$. (b)Similar to (a), but for a given frequency (close to the second rotational alignment frequency) $\hbar\omega = 0.425$ at the $\beta_2 = 0.176$ and $\beta_4 = -0.006$. The full line stands for the positive signature states and the dashed for the negative signature partner band.

At higher rotational frequencies, the behavior changes somewhat. The $ (\pi h_{11/2})^2 $ configuration exerts a strong driving interaction towards positive γ values near the second alignment frequency. Adding the $ (\pi h_{11/2})^2 $ pair may ultimately shift the nucleus towards a positive γ oblate/triaxial shape. This behavior is influenced by the Fermi surface configuration and the rotational alignment of nucleon pairs, which is crucial in dictating the transition from collective to non-collective excitations as observed in these isotopes. The shift from prolate/triaxial to non-collective triaxial/oblate shape is thus a direct consequence of the interaction between the rotational motion and the underlying orbital structure.

Following the second rotational alignment, the collective band structure is lost, and the irregular yrast sequence of an oblate nucleus emerges, with single-particle angular momentum aligned along the short axis.

In summary, phenomenological and empirical laws were applied to indicate shape (phase) evolution in even-even $ ^{126-136} {\rm{Ba}}$, such as $ E_S/E(2_1^+) $, which serves as a global indicator of structural evolution involving axial asymmetry and the shape (phase) evolution from an axially symmetric shape to a γ-soft shape. The γ-unstable shape emerging in $ ^{130} {\rm{Ba}}$ is verified by the TRS calculations in terms of the Woods-Saxon single-particle energy levels as a function of $ \beta_2 $ and γ. It reveals that the medium- to high-Ω orbitals of a high-j shell are significantly affected by γ deformation. Moreover, the analysis of energy ratios ($ R_{6/4} $ versus $ R_{4/2} $) reveals the presence of both collective and non-collective excitations in $ ^{136} {\rm{Ba}}$ ($ N = 80 $), suggesting that a spherical vibrator description may be more appropriate, which influences the non-collective configurations in high spin states as demonstrated by the TRS calculations. These TRS calculations not only reproduce the observed trends but also offer a possible microscopic foundation for the phenomenological and empirical laws, elucidating how specific configurations of single-particle orbitals and nucleon alignments drive the shape evolution and phase transitions in $ ^{126-136} {\rm{Ba}}$.

Additionally, the TRS calculations for even-even $ ^{126-136} {\rm{Ba}}$ illustrate the shape variations linked to the transition in rotational axes, progressing from intermediate-axis rotation to long-axis rotation, and finally to short-axis rotation as the frequency increases. These shape variations are driven by the rotational alignment of specific nucleon pairs at two critical frequencies. Near the first critical frequency ($ \hbar\omega \sim 0.3 $ MeV), the alignment of the $ h_{11/2} $ neutron pair results in a significant negative γ deformation. At the second critical frequency ($ \hbar\omega \sim 0.5 $ MeV), positive γ deformation becomes more favorable due to the rotational alignment of the $ h_{11/2} $ proton pair.

These findings bridge the gap between empirical observations and microscopic nuclear structure, offering deeper insights into the mechanisms driving nuclear deformation and phase transitions.