Predictions for the synthesis of new superheavy nuclei with ²⁵²Cf target

In recent years, the successful synthesis of new superheavy elements (SHEs) with Z = 114-118 has been achieved through fusion reactions with the $ ^{48} {\rm{Ca}}$ projectile and the $ ^{242,244} {\rm{Pu}}$, $ ^{243} {\rm{Am}}$, $ ^{245,248} {\rm{Cm}}$, $ ^{249} {\rm{Bk}}$ and $ ^{249} {\rm{Cf}}$ targets [1−5]. These advancements mark the completion of the seventh period of the periodic table. Theoretical models predict the existence of an “island of stability” within the region around Z = 114, 120, 124 or 126 and N = 184 [6−9]. To synthesize new elements beyond Z = 118 and reach the predicted “island of stability”, many fusion reactions, such as $ ^{64}{\rm{Ni}} $+$ ^{238} {\rm{U}}$, $ ^{58} {\rm{Fe}}$+$ ^{244} {\rm{Pu}}$, $ ^{54} {\rm{Cr}}$+$ ^{248} {\rm{Cm}}$, $ ^{50} {\rm{Ti}}$+$ ^{249} {\rm{Bk}}$, $ ^{50} {\rm{Ti}}$+$ ^{249} {\rm{Cf}}$ and $ ^{51} {\rm{V}}$+$ ^{248} {\rm{Cm}}$, have been experimentally investigated [10−14]. However, no evidence confirming the discovery of the new SHE was detected in these experiments. Therefore, it is essential to establish advanced experimental facilities with improved detection capabilities. Additionally, precise theoretical predictions are crucial for identifying the optimal reaction systems.

Until now, many new isotopes were synthesized using advanced accelerators [15−22]. Based on the experimental results, diverse theoretical approaches have been developed to describe the fusion reactions, including the quantum molecular dynamics (QMD) type model [23−26], the cluster dynamical decay model [27], the fusion-by-diffusion (FBD) model [28, 29], the statistical model [30], the two-step model [31−33], the time-dependent Hartree-Fock (TDHF) theory [29, 34−36] and multidimensional Langevin-type dynamical equations [37−41]. Moreover, the dinuclear system (DNS) model has emerged as a reliable tool [42−61]. In the DNS model, the fusion-evaporation process is divided into the capture, fusion, and survival stages. The reaction system needs to overcome the Coulomb barrier and forms a DNS. The fusion process in the DNS occurs at the bottom of the potential pocket. This is treated as a diffusion process along nucleon degree of freedom guided by the potential energy surface. The fusion probability is determined by solving a set of master equations, while the subsequent de-excitation process is treated via the statistical model.

In searching for the new isotopes at the edge of the SHE region, several experiments based on the $ ^{249-251} {\rm{Cf}}$ targets have been conducted [1, 13, 62−64]. The analysis of these experimental results indicates the feasibility of using Cf targets for the synthesis of neutron-rich superheavy isotopes. Oak Ridge National Laboratory stands as the major global supplier of heavy actinides, with its isotope production program generating a significant quantity of $ ^{252} {\rm{Cf}}$ (10.2 g) in the High Flux Isotope Reactor by multiple neutron capture [65−68]. Besides, the $ ^{252} {\rm{Cf}}$ can also be produced at Research Institute of Atomic Reactors in Russia [69]. Owing to the high neutron excess, the $ ^{252} {\rm{Cf}}$ target holds promise for exploring the boundaries of nuclear existence and offers a potential alternative to the commonly used $ ^{249} {\rm{Cf}}$ target.

For the synthesis of SHE beyond Z = 118, the $ ^{48} {\rm{Ca}}$-induced fusion reactions are limited by the challenges of obtaining a sufficient amount of Es and Fm targets. Therefore, the heavier stable projectiles, such as $ ^{45} {\rm{Sc}}$, $ ^{50} {\rm{Ti}}$, $ ^{51} {\rm{V}}$, $ ^{54} {\rm{Cr}}$ and $ ^{55} {\rm{Mn}}$, can be alternatives in future experiment. Additionally, the employment of neutron-rich radioactive projectiles offers a pathway to explore the N = 184 region. By combining these projectiles with the available $ ^{252} {\rm{Cf}}$ target produced at Oak Ridge National Laboratory, a range of feasible fusion reactions emerges for the production of new superheavy isotopes with Z = 118–123. In this paper, the reliability of the DNS model has been examined. These reactions are investigated within the DNS model, presenting the maximal ER cross sections and corresponding incident energies.

This article is organized as follows: In Sec. II, we describe the theoretical framework of the DNS model. In Sec. III, the reliability of the DNS model has been examined. The calculated results for synthesizing new superheavy nuclei via the stable beams are presented. The dependence of the maximal evaporation residue (ER) cross sections, the optimal incident energies, the capture cross sections, the fusion and survival probabilities on the increasing charge number of the formed compound nuclei are investigated. Additionally, the radioactive beam-induced reactions for reaching the region of N = 184 are also discussed. In Sec. IV, a summary of this work is provided.

In the DNS model, the ER cross section of the fusion reaction can be expressed as a summation over the partial waves $ {J} $ as follows:

In the formula, $ T\left ( E_{\rm{{c.m.}}},J \right ) $ denotes the transmission probability for the colliding nuclei of overcoming the Coulomb barrier. $ P_{\rm{{CN}}}\left ( E_{\rm{{c.m.}}},J\right ) $ is the complete fusion probability for the formation of the compound nucleus [70−73]. The survival probability $ W_{\rm{{sur}}}\left ( E_{\rm{{c.m.}}},J \right ) $ characterizes the likelihood that the formed compound nucleus undergoes de-excitation through neutron emission instead of fission [74]. The expression for the nucleus-nucleus interaction potential incorporating quadrupole deformation can be expressed as [78]:

Here $ \beta_{1,2} $ represent the dynamical quadrupole deformation for projectile and target given by $ C_1 \beta_1^2/C_2 \beta_2^2 = A_1/A_2 $. $ \beta_{1,2}^{0} $ denote the static deformation parameters, which usually taken as the quadrupole deformation parameters [6]. $ \theta_{1,2} $ are the collision angles of statically deformed projectile and target. The tip-tip collision favors nucleon transfer and is chosen in the calculation [75]. $ C_{1,2} $ are the stiffness parameters of the nuclear surface given by the liquid drop model [76]. The Coulomb potential $ V_{\mathrm{C}} $ is calculated by Wong formula [77]:

The nuclear potential $ V_{\mathrm{N}} $ is described by the double-folding potential in the sudden approximation [78, 79]:

with

Here $ C_{0} $ = 300 MeV$ \cdot\mathrm{fm^{3}} $, $ f_{\mathrm{in}} $ = 0.09, $ f_{\mathrm{ex}} $ = -2.59, $ f_{\mathrm{in}}^{'} $ = 0.42 and $ f_{\mathrm{ex}}^{'} $ = 0.54 [79]. $ Z_{1,2} $ and $ N_{1,2} $ are the proton and neutron numbers of the nuclei. $ \rho_{1} $ and $ \rho_{2} $ are the nuclear density distribution functions taken as the two-parameter Woods-Saxon types as follows:

and

Here $ \rho_{0} $ = 0.17 fm^-3, and the surface diffusion coefficients $ a_{1,2} $ are taken as 0.55 fm. $ \Re _1(\theta_1) $ and $ R_2(\theta_2) $ are the surface radii of the nuclei calculated as follows:

$ R_{i} $ denote the spherical radii of the nuclei, $ Y_{2}^{0}(\theta) $ is the spherical harmonic function of degree 2 and order 0.

The capture cross section $ \sigma _{\rm{{cap}}} $ can be written as [48]:

Considering the barrier distribution, the transmission probability of overcoming the Coulomb barrier can be expressed as [54]:

$ T({E_{\rm{{c.m.}}}},B,J) $ is the transmission probability calculated by the Ahmed formula [54, 80−82], with the approximation of the total interaction potential energy around the barrier decided by the selected $ V_{\mathrm{C}} $ and $ V_{\mathrm{N}} $.

The barrier distribution function $ f\left ( B \right ) $ is taken as an asymmteric Gaussian function [54]:

Here B is the Coulomb barrier. $ B_\mathrm{m} = a V_\mathrm{B}^\mathrm{Sp} + (1 - a)V_\mathrm{B}^\mathrm{S} $, $ \Delta_1 = \dfrac{b}{2}(C_1 \left( \beta_1^S \right)^2+C_2 \left( \beta_2^S \right)^2) $, $ \Delta_2 = \dfrac{c}{2}(C_1 \left( \beta_1^S \right)^2+C_2 \left( \beta_2^S \right)^2) $. $ \beta_{1,2}^S $ correspond to the deformation parameters of the projectile and the target at the saddle-point configuration, $ V_\mathrm{B}^\mathrm{Sp} $ represents the Coulomb barrier of the configuration with two spherical nuclei. $ V_\mathrm{B}^\mathrm{S} $ denotes the Coulomb barrier at the saddle point. For deformed systems, the values of the parameters are a = 0.37, b = 0.12, c = 1.12 [83].

Within the dinuclear system, the nucleon transfer process is driven by the potential energy surface along the mass asymmetry degree $ \eta = \left(A_{1}-A_{2}\right) /\left(A_{1}+A_{2}\right) $. The potential energy surface is defined as [48]:

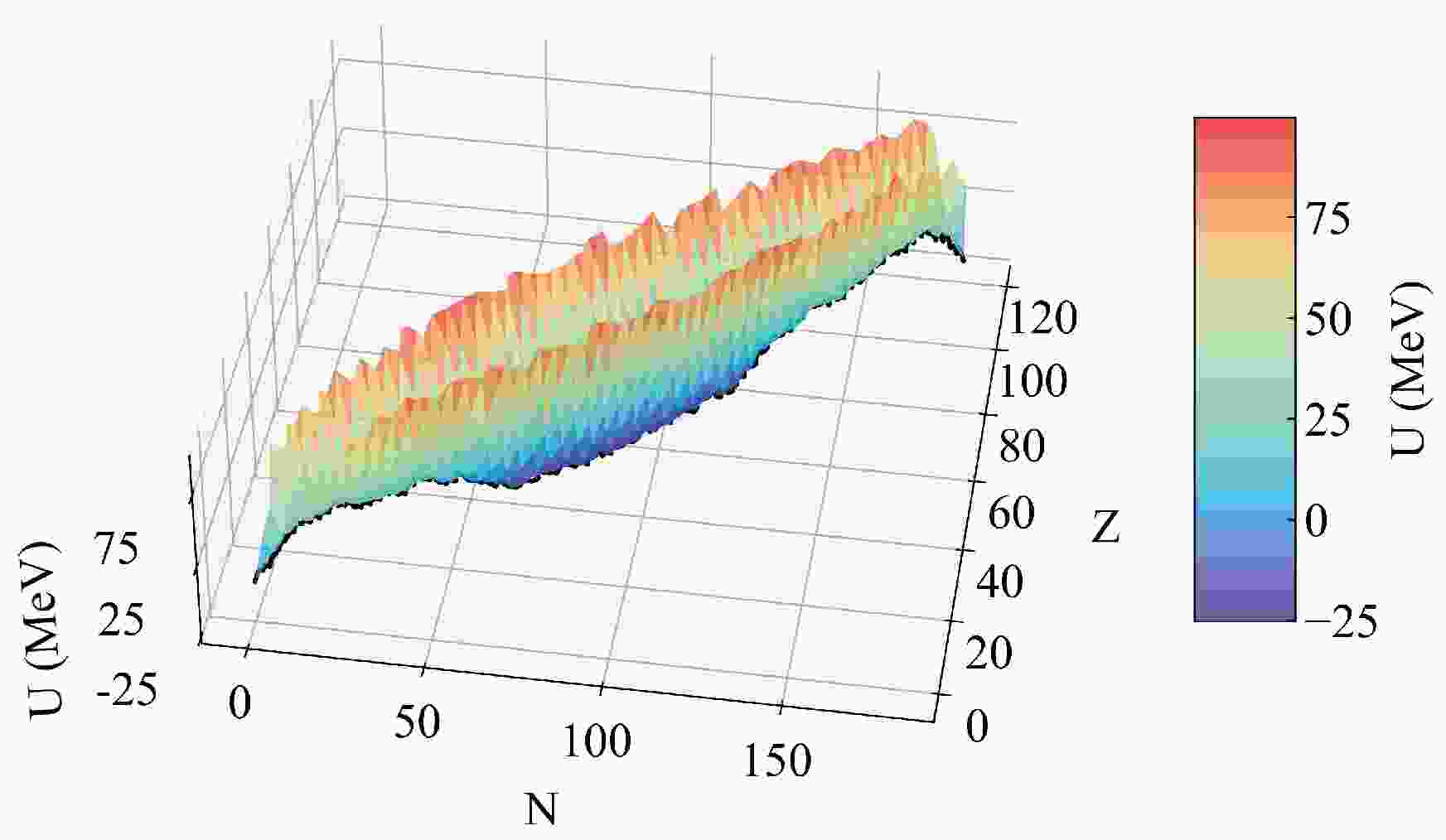
Here, $ {E_{\rm{B}}}\left( {Z,N} \right) $, $ {E_{\rm{B}}}\left( {{Z_{\rm{1}}},{N_{\rm{1}}}} \right) $ and $ {E_{\rm{B}}}\left( {{Z_{\rm{2}}},{N_{\rm{2}}}} \right) $ represent the binding energies of the compound nucleus, the projectile and the target given by the macroscopic-microscopic model [6], with the shell and pairing corrections included. $ V^\mathrm{CN}_\mathrm{rot} $, $ V_{\mathrm{C}} $ and $ V_{\mathrm{N}} $ are the rotation energy of the compound nuclei, Coulomb potential and nuclear potential, respectively.

Fig. 1 presents the potential energy surface of the reaction $ ^{48}\mathrm{Ca} + ^{249} {\rm{Cf}}$. In the fusion stage, the nucleon transfer process occurs at the nadir of the potential energy surface. This minimal trajectory along the degree of η is defined as the driving potential, as plotted in Fig. 2. The difference in driving potential from the peak at the Businaro-Gallone (B.G.) point to the incident point is defined as the inner fusion barrier, expressed as $ {B_{\mathrm{fus}}} = U\left( {{\eta _\mathrm{B.G.}}} \right) - U\left( {{\eta _\mathrm{i}}} \right) $ [84, 85]. For the reaction $ ^{48}\mathrm{Ca} + ^{249} {\rm{Cf}}$, the $ {B_{\mathrm{fus}}} $ value is 12.23 MeV. This substantial inner fusion barrier height poses a challenge to the fusion process. The compound nucleus is formed when the dinuclear system surpasses the $ {B_{\mathrm{fus}}} $, failing to surpass this barrier results in the quasi-fission process. Consequently, the fusion probability $ P_{\mathrm{CN}} $ is determined by the summation of the distribution probabilities of overcoming the inner fusion barrier, which is determined by the selected $ V_{\mathrm{C}} $ and $ V_{\mathrm{N}} $, as follows [54]: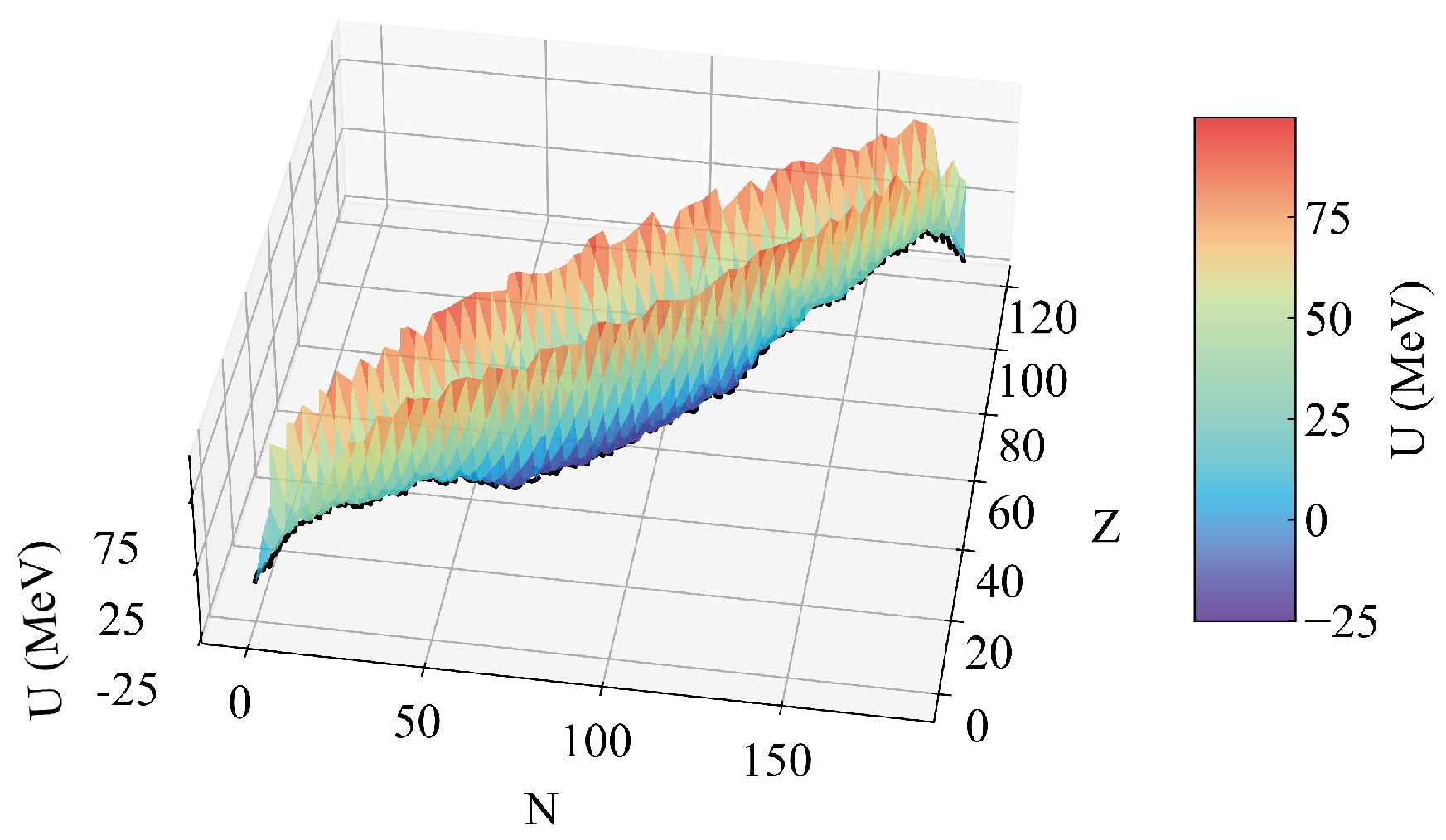

Figure 1.  (Color online) The potential energy surface of the reaction $ ^{48}\mathrm{Ca} + ^{249} {\rm{Cf}}$ at J = 0. The black line indicates the valley of the potential energy surface.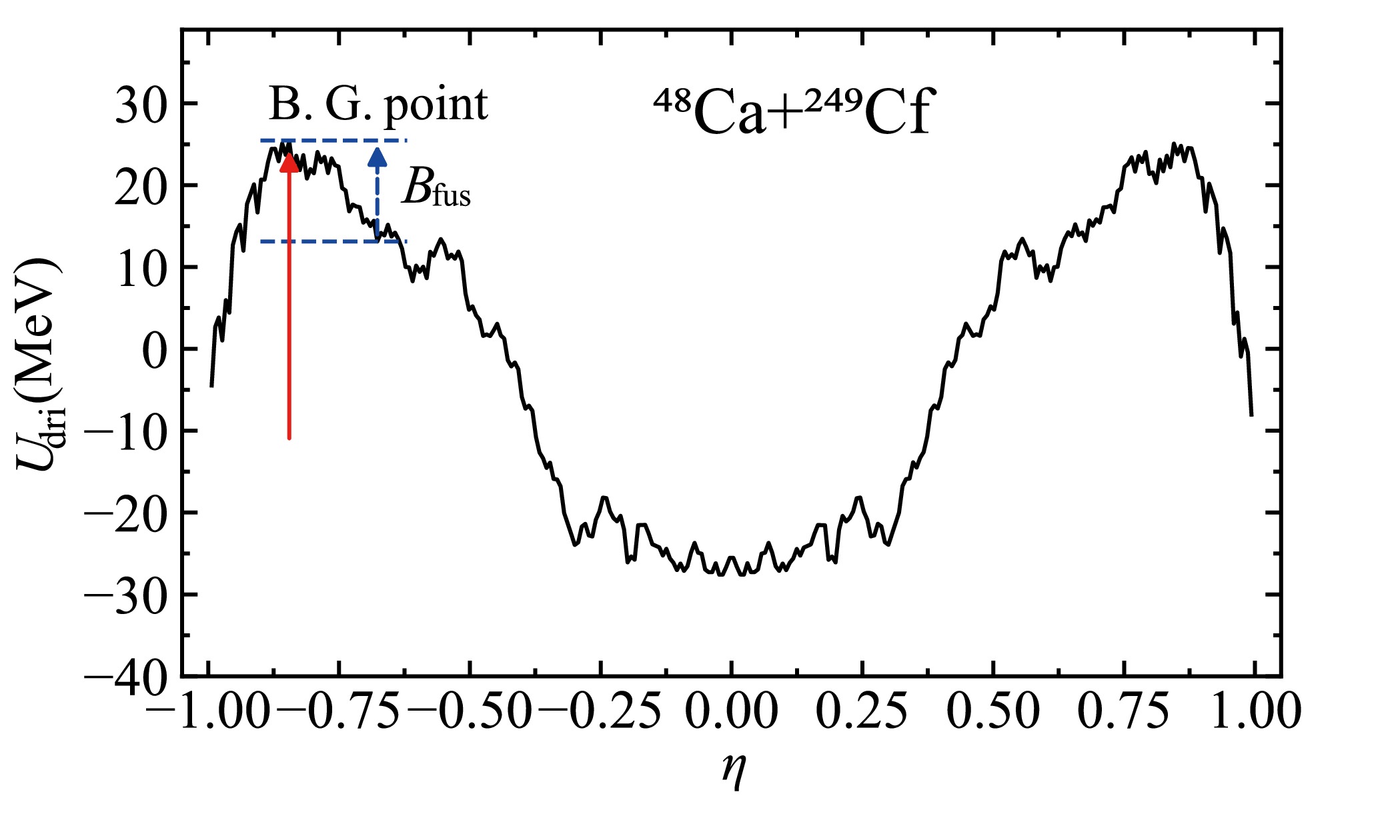

Figure 2.  (Color online) The driving potential of the reaction $^{48}\mathrm{Ca} + ^{249}{\rm{Cf}}$ as a function of mass asymmetry at J = 0. The entrance channel is represented by the blue dashed arrow. The red solid arrow denotes the B.G. point.

The interaction time $ \tau_{\mathrm{int}}(J) $ is determined using the deflection function method [86]. The distribution probability $ P\left ( Z_{\rm{{1}}},N_{\rm{{1}}},E_{\rm{{1}}},t \right ) $ is obtained through the solution of the two-dimensional master equation:

The nucleon transfer process is driven by the potential energy surface, with the local excitation energy serving as a key factor. The local excitation energy $ \varepsilon^* $ is determined by the dissipation of relative motion along the potential energy surface and is expressed as $ \varepsilon^*(t) = E^{\text{diss}}(t) - \left[ U({Z_1},{N_1},{Z_2},{N_2}) - U({Z_\mathrm{P}},{N_\mathrm{P}},{Z_\mathrm{T}},{N_\mathrm{T}}) \right] $ [75]. The excitation energy $ E_{1} $ for state $ (Z_{1}, N_{1}) $ is then calculated as $ E_{1} = \varepsilon^*(t = \tau_{\mathrm{int}})A_1/A $, where A is mass number of compound nuclei.

The potential energy surface not only determines the local excitation energy but also influences the nucleon transfer rate by influencing energy dissipation, thereby playing a crucial role in the dynamic evolution of the master equation. $ W_{{Z_{1}, N_{1}; Z_{1}^{\prime}, N_{1}}} $ represents the mean transition probability from state $ (Z_{1}, N_{1}) $ to state $ (Z_{1}^{\prime}, N_{1}) $ [87], $ d_{Z_1, N_1} $ is the microscopic dimension for the corresponding state. The quasi-fission rate $ \Lambda_{\mathrm{qf}} $ and fission rate $ \Lambda_{\mathrm{fis}} $ is determined by the one-dimensional Kramers formula [88], with the local temperature given by the Fermi gas model $ \Theta(t) = \left( \dfrac{\varepsilon^*(t)}{A / 12} \right)^{1/2} $. The energy dissipated into the DNS is expressed as $ E^{\text{diss}}(J, t) = E_{\text{c.m.}} - B - \dfrac{\left(J'(t)\hbar\right)^2}{2\zeta_{\text{rel}}} - E_{\text{rad}}(J, t) $. Here $ E_{\text{rad}}(J, t) = \left[E_{\text{c.m.}} - B - \dfrac{\left(J\hbar\right)^2}{2\zeta_{\text{rel}}}\right] e^{-t/\tau_R} $ represents the radial energy. $ J'(t) = J_{\text{st}} + (J - J_{\text{st}})e^{-t/\tau_J}) $ is the relative angular momentum at time t. $ J_{\text{st}} = \dfrac{\zeta_{\text{rel}}}{\zeta_{\text{tot}}}J $ and J is the initial entrance angular momentum. $ \zeta_{\text{rel}} $ and $ \zeta_{\text{tot}} $ are the relative and total moments of inertia, respectively. The characteristic relaxation times are $ \tau_R = 2 \times 10^{-22} \, \text{s} $ for the radial energy and $ \tau_J = 12 \times 10^{-22} \, \text{s} $ for the angular momentum.

The motion of nucleons is described by the single-particle Hamiltonian $ H(t) = H_0(t) + V(t) $ [75], with

Here $ K,K' $ refer to the fragment 1 and 2, respectively. $ \varepsilon_{\nu_K} $ and $ u_{\alpha_K,\beta_{K'}} $ represent the single-particle energies and interaction matrix elements, respectively. The single-particle matrix element can be parameterized as follows [89]:

$ U_{K,K'}(t) $ and $ \delta_{\alpha_K, \beta_{K'}} $ are detailed in Refs. [48, 90]. The proton transition probability is microscopically derived as follows:

The expression for neutron transition probability is analogous. The memory time is given by $ \tau_{\text{mem}} = \hbar \left[ 2\pi/\sum\nolimits_{KK'} V_{K,K'} V^*_{K,K'} \right]^{1/2} $. The matrix element V of the interaction potential in Eq. (16) is considered to result from nucleon transfer between the two Fermi surfaces of the dinuclear system fragments [91].

During the evolution process of the relative motion, the nuclei becomes excited due to the dissipation of relative kinetic energy. The excitation energy opens a valence space $ \Delta \varepsilon_K = \sqrt{\frac{4 \varepsilon^*_K}{g_K}} $ in fragment K. Only the particles in this valence space are actively involved in excitation and transfer processes. The averages of these quantities are calculated within the valence space, with $ \varepsilon^*_K = \varepsilon^* \frac{A_K}{A} $ and $ g_K = \frac{A_K}{12} $. The number of valence states is given by $ N_K = g_K\Delta \varepsilon_K $, and the number of valence nucleons is $ m_K = N_K/2 $. This leads to the expression of the dimension $ d(m_1, m_2) = \binom{N_1}{m_1} \binom{N_2}{m_2} $ [75, 89].

In the survival stage, the primary competition arises between fission and neutron emission [47]. The survival probability of emitting x neutrons is calculated by the statistical model as follows:

$ P\left(E_{\mathrm{CN}}^{*}, x, J\right) $ denotes the realization probability for emitting x neutrons [92]. $ E_{i}^{*} $ is the excitation energy of the compound nucleus before the emission of the i-th neutron. The partial decay width for the evaporation of neutron $ \Gamma_{\rm{{n}}} $ and the fission decay width $ \Gamma_{\rm{{f}}} $ can be calculated with the Weisskopf-Ewing theory [93] and the Bohr-Wheeler transition-state method [94]. The temperature-dependent fission barrier is expressed as follows [54, 95, 96]:

Here $ {B_{\rm{f}}}^{\rm{LD}} $ is the macroscopic part of the fission barrier and $ {B_{\rm{f}}}^{\rm{M}} $ denote the microscopic part given by the microscopic shell correction energy at the ground state [6]. $ x_{\rm{LD}} $ and $ T_{i} $ represent the temperature dependent parameter and the nuclear temperature, respectively [54, 95]. $ {E_{\rm{D}}} $ is the shell damping energy [54]. $ J_{\rm{g.s.}} $ and $ J_{\rm{s.d.}} $ are the moments of inertia of the compound nucleus in the ground state and at the saddle point, respectively [97, 98].

In order to verify the reliability of utilizing the DNS model for predicting the synthesis of the new superheavy nuclei, the theoretical results based on the DNS model are compared with the corresponding experimental data for fusion reactions $ ^{48} {\rm{Ca}}$+$ ^{245} {\rm{Cm}}$$ \rightarrow $$ ^{293-\mathrm{xn}} {\rm{Lv}}+{\rm{xn}}$, $ ^{48} {\rm{Ca}}$+$ ^{248} {\rm{Cm}}$$ \rightarrow $$ ^{296-\mathrm{xn}} {\rm{Lv}}+{\rm{xn}}$, $ ^{48} {\rm{Ca}}$+$ ^{249} {\rm{Bk}}$$ \rightarrow $$ ^{297-\mathrm{xn}} {\rm{Ts}}+{\rm{xn}}$ and $ ^{48} {\rm{Ca}}$+$ ^{249} {\rm{Cf}}$$ \rightarrow $$ ^{297-\mathrm{xn}} {\rm{Og}}$+xn, as shown Fig. 3. Theoretically, the existence of superheavy nuclei with Z > 104 is primarily due to the shell effect. The calculation of the fission barrier heavily relies on the contribution of the shell correction, and the reduction of the shell correction with increasing excitation energy is described by the $ {E_{\rm{D}}} $ values. Fig. 3 illustrates that the subjective selection range of $ {E_\mathrm{D}} $ (22-30 MeV) [102, 103] can result in an order of magnitude error range in the calculated ER cross sections. The influence of $ {E_\mathrm{D}} $ intensifies with the increasing number of the evaporated neutrons, expanding the error range, while the optimal incident energies remain insensitive to the $ {E_\mathrm{D}} $ range.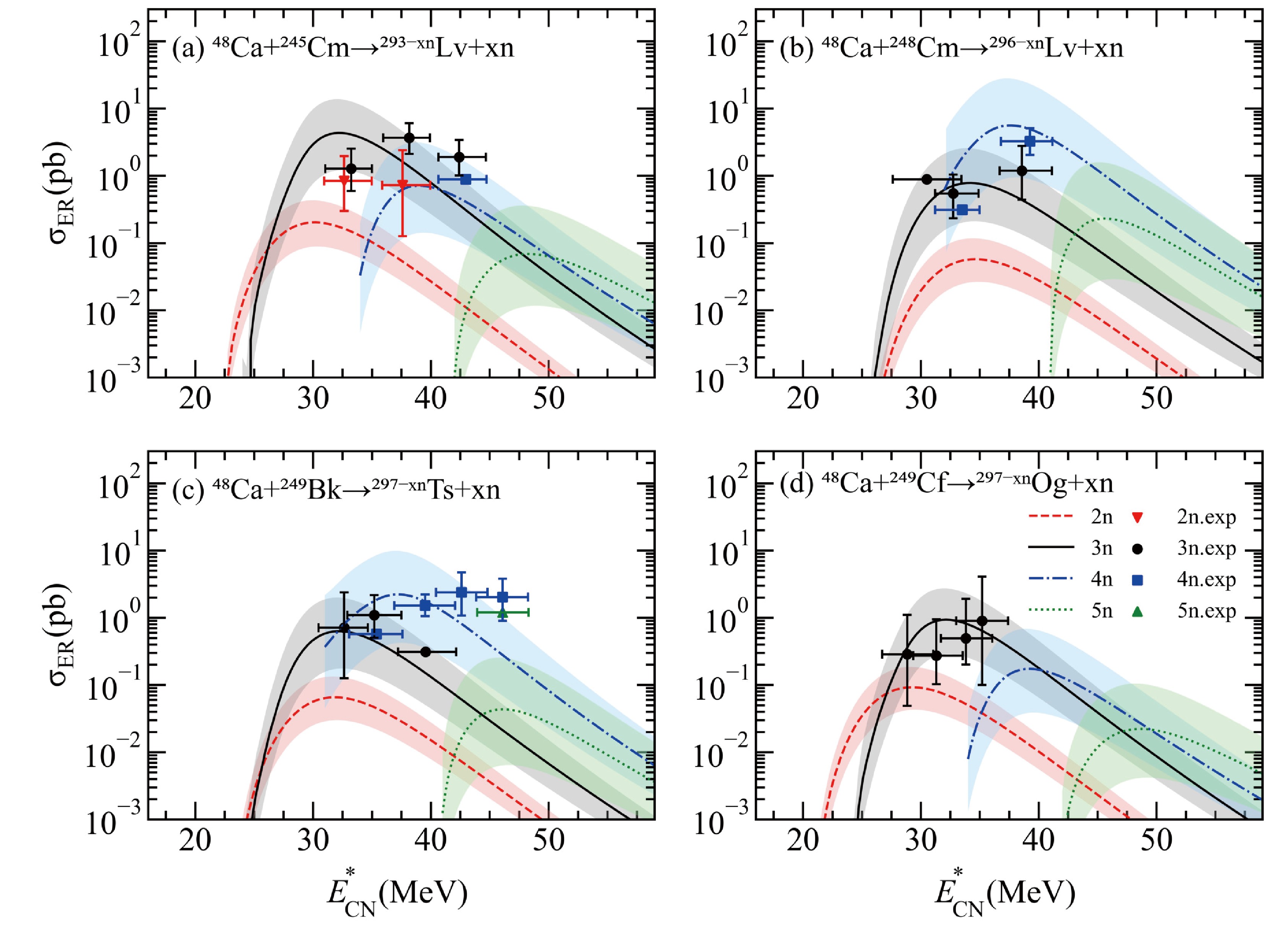

Figure 3.  (Color online) Comparison of the calculated results with the available experimental data [1, 62, 64, 99−101]. The calculated ER cross sections in the 2n, 3n, 4n, and 5n channels are denoted by the red dashed lines, black solid lines, blue dash-dotted lines, and green dotted lines, respectively. The experimental data for the 2n, 3n, 4n, and 5n channels are presented by the solid red inverted triangles, black circles, blue squares, and green triangles with the error bars, respectively.

In Fig. 3, an agreement is observed between the ER cross sections calculated by the DNS model and experimental data [1, 62, 64, 99−101], with the deviations well within acceptable error margins. The difference between the experimental and calculated values of the single data of the 5n-emission channel in Fig. 3 (c) can be attributed to the suppressed survival probability given by the statistical model. The DNS model predicts a maximal ER cross section of $ 4.3 ^{+9.5}_{-3.1} $ pb for the reaction $ ^{48} {\rm{Ca}}$+$ ^{245} {\rm{Cm}}$ at the 3n-emission channel, $ 5.6 ^{+22.4}_{-4.6} $ pb for the reaction $ ^{48} {\rm{Ca}}$+$ ^{248} {\rm{Cm}}$ at the 4n-emission channel, $ 2.2^{+7.7}_{-1.8} $ pb for the reaction $ ^{48} {\rm{Ca}}$+$ ^{249} {\rm{Bk}}$ at the 4n-emission channel and $ 0.9^{+1.8}_{-0.7} $ pb for the reaction $ ^{48} {\rm{Ca}}$+$ ^{249} {\rm{Cf}}$ at the 3n-emission channel. These predictions align well with the corresponding experimental values of $ 3.7 ^{+3.6}_{-1.8} $ pb, $ 4.5 ^{+3.6}_{-1.9} $ pb, $ 2.4 ^{+3.3}_{-1.4} $ pb and $ 0.9 ^{+3.2}_{-0.8} $ pb, respectively, at the same emission channel. These results provide support for the application of the DNS model in predicting the optimal projectile-target combinations and the corresponding incident energies for producing new superheavy nuclei.

In Table 1, the ER cross sections for the production of new isotopes with Z = 118-123 via the $ ^{252} {\rm{Cf}}$-based reactions employing the $ ^{48}\mathrm{Ca} $, $ ^{45}\mathrm{Sc} $, $ ^{50}\mathrm{Ti} $, $ ^{51}\mathrm{V} $, $ ^{54}\mathrm{Cr} $ and $ ^{55}\mathrm{Mn} $ projectiles are presented. The new isotopes $ ^{297} {\rm{Og}}$, $ ^{296} {\rm{Og}}$ and $ ^{295} {\rm{Og}}$ can be produced via the 3n, 4n and 5n-emission channel of the reaction $ ^{48}\mathrm{Ca} $+$ ^{252} {\rm{Cf}}$, with maximal ER cross sections of 94,470 and 71 fb, respectively. For synthesizing new elements with Z = 119-123, the reactions $ ^{45} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{294} {\rm{119}}$+3n (140 fb at 204.0 MeV), $ ^{50} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{299} {\rm{120}}$+3n (3.4 fb at 226.3 MeV), $ ^{51} {\rm{V}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{300} {\rm{121}}$+3n (0.61 fb at 234.5 MeV), $ ^{54} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{303} {\rm{122}}$+3n (0.018 fb at 249.8 MeV), $ ^{55} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{304} {\rm{123}}$+3n (0.0018 fb at 259.6 MeV) are worthy of further investigation. Notably, for the reaction $ ^{48} {\rm{Ca}}$+$ ^{252} {\rm{Cf}}$, the maximal ER cross section is observed in the 4n-emission channel. For the other $ ^{252} {\rm{Cf}}$ based reactions, the maximal ER cross sections appear in the 3n-emission channel, and these maximal ER cross sections decreases with the increasing charge number of the formed compound nuclei.

$\mathrm{Reaction\ Channel}$	$E_{\mathrm{c.m.}}$ (MeV)	$E^{*}_\mathrm{CN}$ (MeV)	$\sigma_{\mathrm{ER}}^{\mathrm{max}}$ (fb)
$^{48}{\rm{Ca}}$+$^{252}{\rm{Cf}}$ $\rightarrow$ $^{297}{\rm{Og}}$+3n	$205.8$	$33.0$	$ 9.4 ^{+17.7}_{-6.5}\times10^{1}$
$^{296}{\rm{Og}}$+4n	$210.8$	$38.0$	$ 4.7 ^{+14.7}_{-3.7}\times10^{2}$
$^{295}{\rm{Og}}$+5n	$217.8$	$45.0$	$ 7.1 ^{+32.7}_{-6.0}\times10^{1}$
$^{45}$Sc+$^{252}{\rm{Cf}}$ $\rightarrow$ $^{294}{\rm{119}}$+3n	$204.0$	$34.0$	$ 1.4 ^{+2.6}_{-1.0}\times10^{2}$
$^{293}{\rm{119}}$+4n	$212.0$	$42.0$	$ 5.0 ^{+13.2}_{-3.7}\times10^{1}$
$^{292}{\rm{119}}$+5n	$223.0$	$53.0$	$ 5.1 ^{+16.6}_{-4.0}\times10^{-1}$
$^{50}{\rm{Ti}}$+$^{252}{\rm{Cf}}$ $\rightarrow$ $^{299}{\rm{120}}$+3n	$226.3$	$34.0$	$ 3.4 ^{+5.3}_{-2.2}$
$^{298}{\rm{120}}$+4n	$234.3$	$42.0$	$ 8.2 ^{+19.5}_{-5.9}\times10^{-1}$
$^{297}{\rm{120}}$+5n	$244.3$	$52.0$	$ 1.2 ^{+3.6}_{-0.9}\times10^{-1}$
$^{51}{\rm{V}}$+$^{252}{\rm{Cf}}$ $\rightarrow$ $^{300}{\rm{121}}$+3n	$234.5$	$34.0$	$ 6.1 ^{+8.4}_{-3.8}\times10^{-1}$
$^{299}{\rm{121}}$+4n	$243.5$	$43.0$	$ 2.3 ^{+4.5}_{-1.6}\times10^{-1}$
$^{298}{\rm{121}}$+5n	$255.5$	$55.0$	$ 3.3 ^{+7.4}_{-2.2}\times10^{-3}$
$^{54}{\rm{Cr}}$+$^{252}{\rm{Cf}}$ $\rightarrow$ $^{303}{\rm{122}}$+3n	$249.8$	$35.0$	$ 1.8 ^{+1.8}_{-1.0}\times10^{-2}$
$^{302}{\rm{122}}$+4n	$260.8$	$46.0$	$ 6.1 ^{+8.4}_{-3.6}\times10^{-3}$
$^{301}{\rm{122}}$+5n	$273.8$	$59.0$	$ 5.0 ^{+6.5}_{-2.9}\times10^{-4}$
$^{55}{\rm{Mn}}$+$^{252}{\rm{Cf}}$$\rightarrow$ $^{304}{\rm{123}}$+3n	$259.6$	$36.0$	$ 1.8 ^{+1.5}_{-0.9}\times10^{-3}$
$^{303}{\rm{123}}$+4n	$270.6$	$47.0$	$ 4.4 ^{+4.9}_{-2.2}\times10^{-4}$
$^{302}{\rm{123}}$+5n	$292.6$	$69.0$	$ 2.5 ^{+2.0}_{-0.7}\times10^{-5}$

Table 1.  The $^{252}{\rm{Cf}}$-based reaction systems for producing new superheavy nuclei. The reaction channels, the optimal incident energies $E_{\mathrm{c.m.}}$, the corresponding excitation energies $E^{*}_{\mathrm{CN}}$ and the maximal ER cross sections $\sigma_{\mathrm{ER}}^{\mathrm{max}}$ are listed in columns 1-4, respectively.

To further investigate the influence of the proton number of the formed compound nucleus $ Z_{\rm{CN}} $ on the synthesis of new elements with Z = 119-123, the predicted maximal ER cross sections, the optimal incident energies and the Q values of the corresponding reactions are presented in Fig. 4. Fig. 4(a) illustrates an exponential decrease in the ER cross sections with the increasing $ Z_{\rm{CN}} $. In Fig. 4(b), the corresponding optimal incident energies increase with the rising $ Z_{\rm{CN}} $. It is noteworthy, as revealed in Table. I, that the corresponding $ E^{*}_{\rm{CN}} $ fall within the range of 33-36 MeV, thereby exerting a limited impact on the optimal incident energies. The observed variations in the optimal incident energies can be attributed to the distinct Q values, as depicted in Fig. 4(c). A higher $ Z_{\rm{CN}} $ suppresses the Q value of the reaction system, consequently enhancing the optimal incident energy.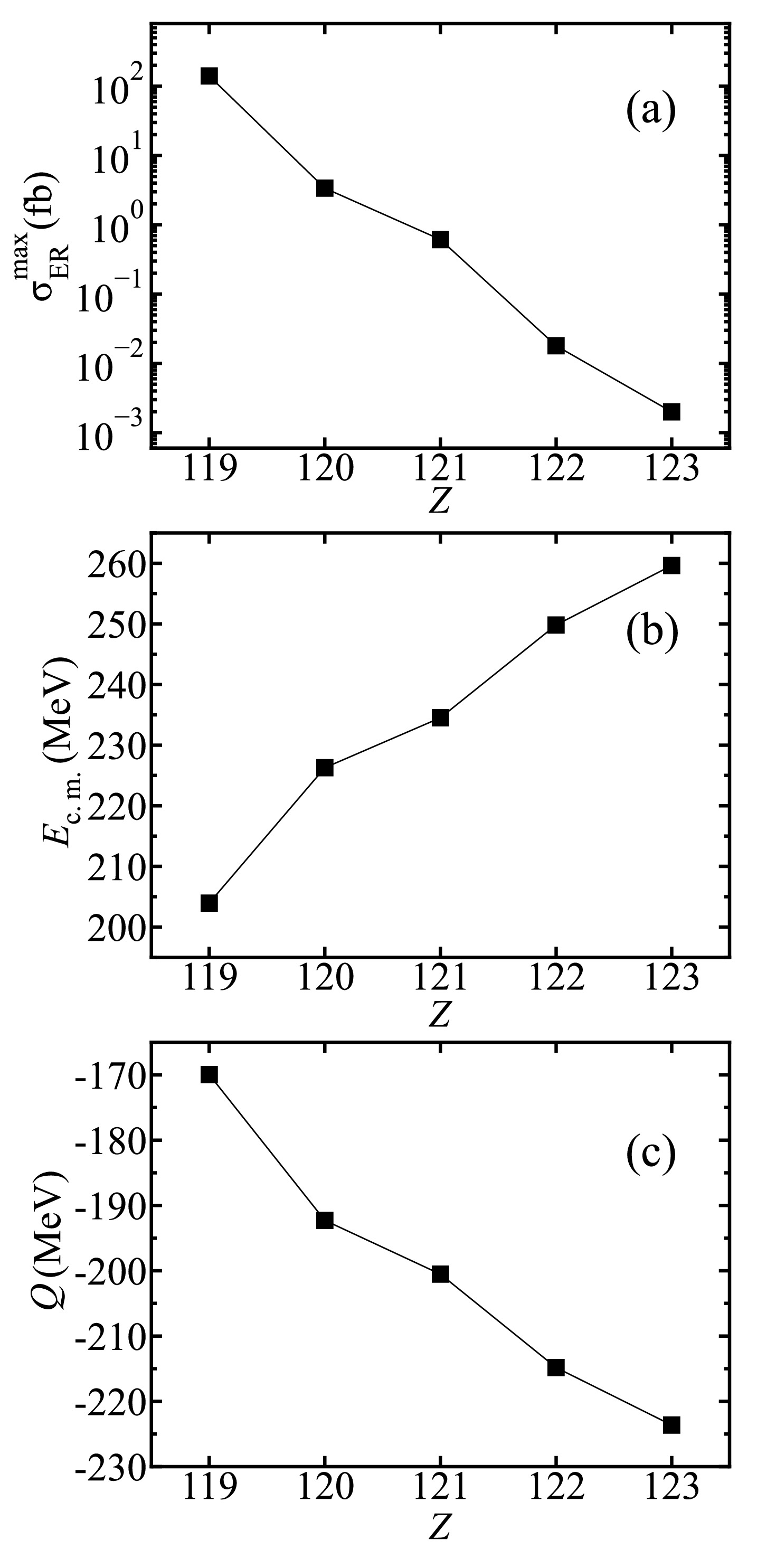

Figure 4.  (Color online) (a) The calculated maximal ER cross sections, (b) the corresponding optimal incident energies and (c) the Q values for the synthesis of the SHEs with Z = 119-123 via the reactions $ ^{45}\mathrm{Sc} + ^{252} {\rm{Cf}}$, $ ^{50}\mathrm{Ti} + ^{252} {\rm{Cf}}$, $ ^{51}\mathrm{V} + ^{252} {\rm{Cf}}$, $ ^{54}\mathrm{Cr} + ^{252} {\rm{Cf}}$ and $ ^{55}\mathrm{Mn} + ^{252} {\rm{Cf}}$.

For an comprehensive investigation into the influence of $ Z_{\rm{CN}} $ on the maximal ER cross sections, thorough discussions of the capture, fusion, and survival stages are essential. In Fig. 5(a) the capture cross sections for producing new elements with Z = 119-123 with the $ ^{252} {\rm{Cf}}$ target at $ E^{*}_{\rm{CN}} $ = 35, 40 and 45 MeV are plotted. It reveals an increase in the capture cross sections with rising $ E_{\mathrm{CN}}^{*} $ due to the escalating probability of overcoming the Coulomb barrier. The capture cross sections show an increasing trend with apparent odd-even staggering, which can be attributed to the influence of the Coulomb barrier. Fig. 5(b) illustrates the excitation energies associated with the Coulomb barriers $ V_{\rm{b}}+Q $ for the corresponding reactions. It can be observed that the $ V_{\rm{b}}+Q $ values have a decreasing trend with the ascending $ Z_{\rm{CN}} $, and the $ V_{\rm{b}}+Q $ values are lower for SHE with even $ Z_{\rm{CN}} $, resulting in the aforementioned increasing trend and odd-even staggering of the capture cross section with the rise of $ Z_{\rm{CN}} $.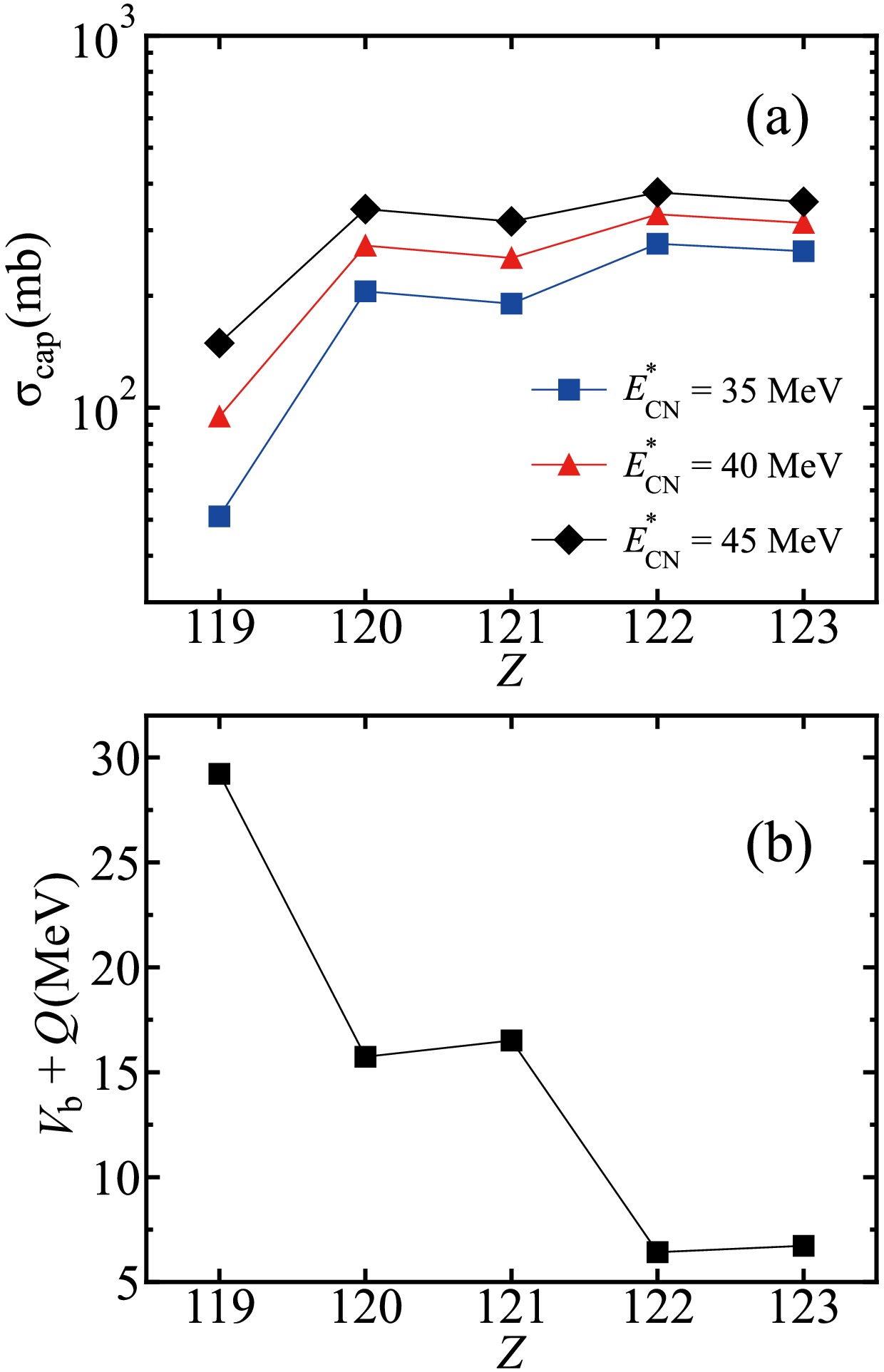

Figure 5.  (Color online) (a) The calculated capture cross sections for the synthesis of the SHEs with Z = 119-123 via the reactions $^{45}\mathrm{Sc} + ^{252}{\rm{Cf}}$, $^{50}\mathrm{Ti} + ^{252}{\rm{Cf}}$, $^{51}\mathrm{V} + ^{252}{\rm{Cf}}$, $^{54}\mathrm{Cr} + ^{252}{\rm{Cf}}$ and $^{55}\mathrm{Mn} + ^{252}{\rm{Cf}}$ with $E^{*}_{\rm{CN}}$ = 35 MeV, 40 MeV and 45 MeV. (b) The excitation energies of the corresponding Coulomb barriers of the reactions $^{45}\mathrm{Sc} + ^{252}{\rm{Cf}}$, $^{50}\mathrm{Ti} + ^{252}{\rm{Cf}}$, $^{51}\mathrm{V} + ^{252}{\rm{Cf}}$, $^{54}\mathrm{Cr} + ^{252}{\rm{Cf}}$ and $^{55}\mathrm{Mn} + ^{252}{\rm{Cf}}$.

For the fusion stage, Fig. 6(a) presents the fusion probabilities for synthesizing new elements with Z = 119-123 at $ E^{*}_{\rm{CN}} $ = 35, 40 and 45 MeV. The fusion probabilities exhibit an enhancement with higher $ E^{*}_{\rm{CN}} $, driven by the increased likelihood of overcoming the inner fusion barrier. A decreasing trend in the fusion probabilities is observed with the ascending $ Z_{\rm{CN}} $, especially between Z = 119–120 and Z = 121–122. This trend can be attributed to the different inner fusion barriers. Fig. 6(b) complements this analysis by presenting the $ B_{\rm{fus}} $ values of the corresponding reactions. It reveals that the $ B_{\rm{fus}} $ value increases with the rise of $ Z_{\rm{CN}} $, notably between the $ ^{45} {\rm{Sc}}$-induced reaction and $ ^{50} {\rm{Ti}}$-induced reaction, as well as between the $ ^{51} {\rm{V}}$-induced reaction and $ ^{54} {\rm{Cr}}$-induced reaction. The rise in the mass number of the projectile contributes to an increased mass asymmetry in the reaction system, and the entrance channel deviates from the B.G. point, resulting in the higher $ B_{\rm{fus}} $ value. The $ B_{\rm{fus}} $ value also increases with rising angular momentum. The high inner fusion barrier hinders the fusion process, leading to the suppressed fusion probability.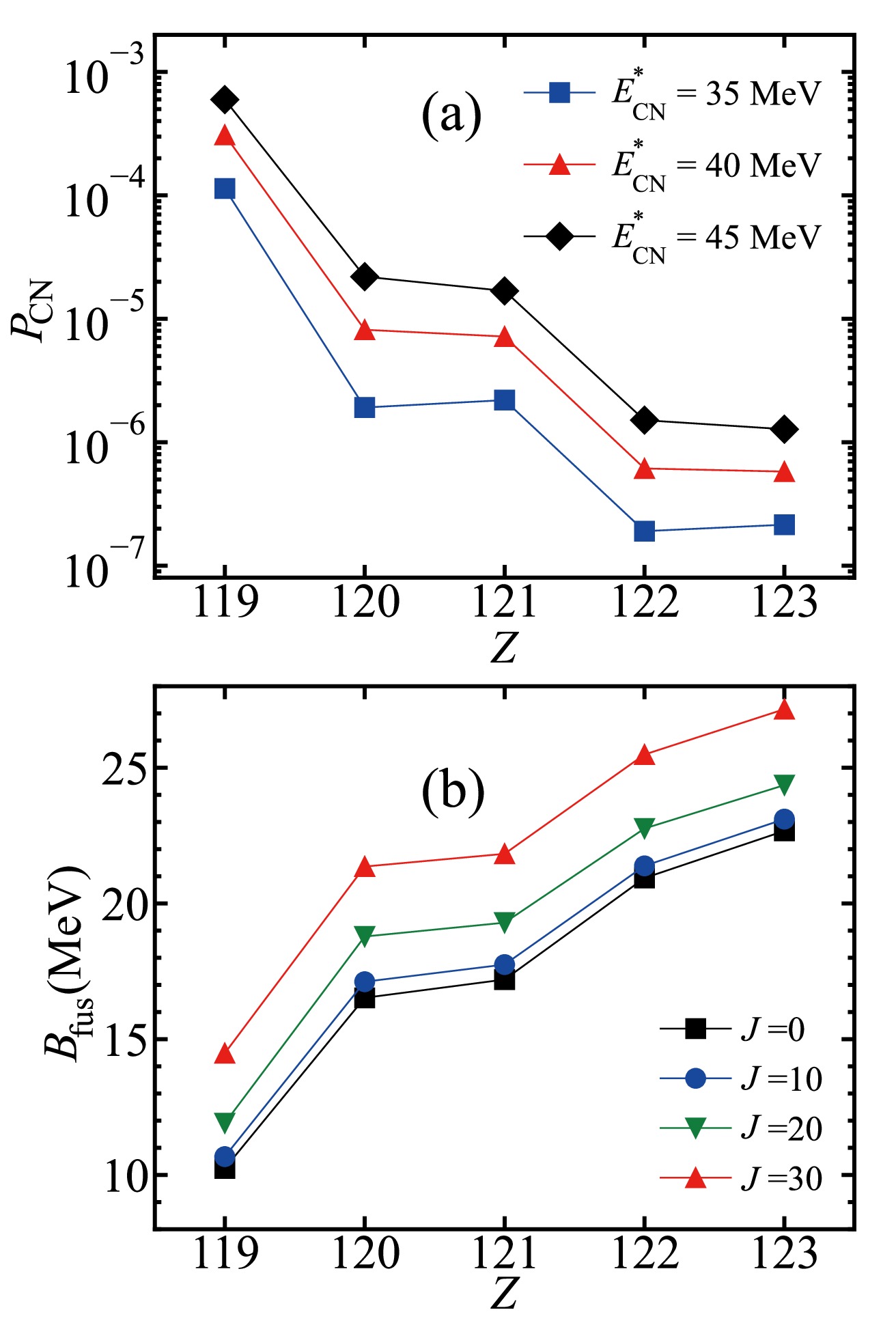

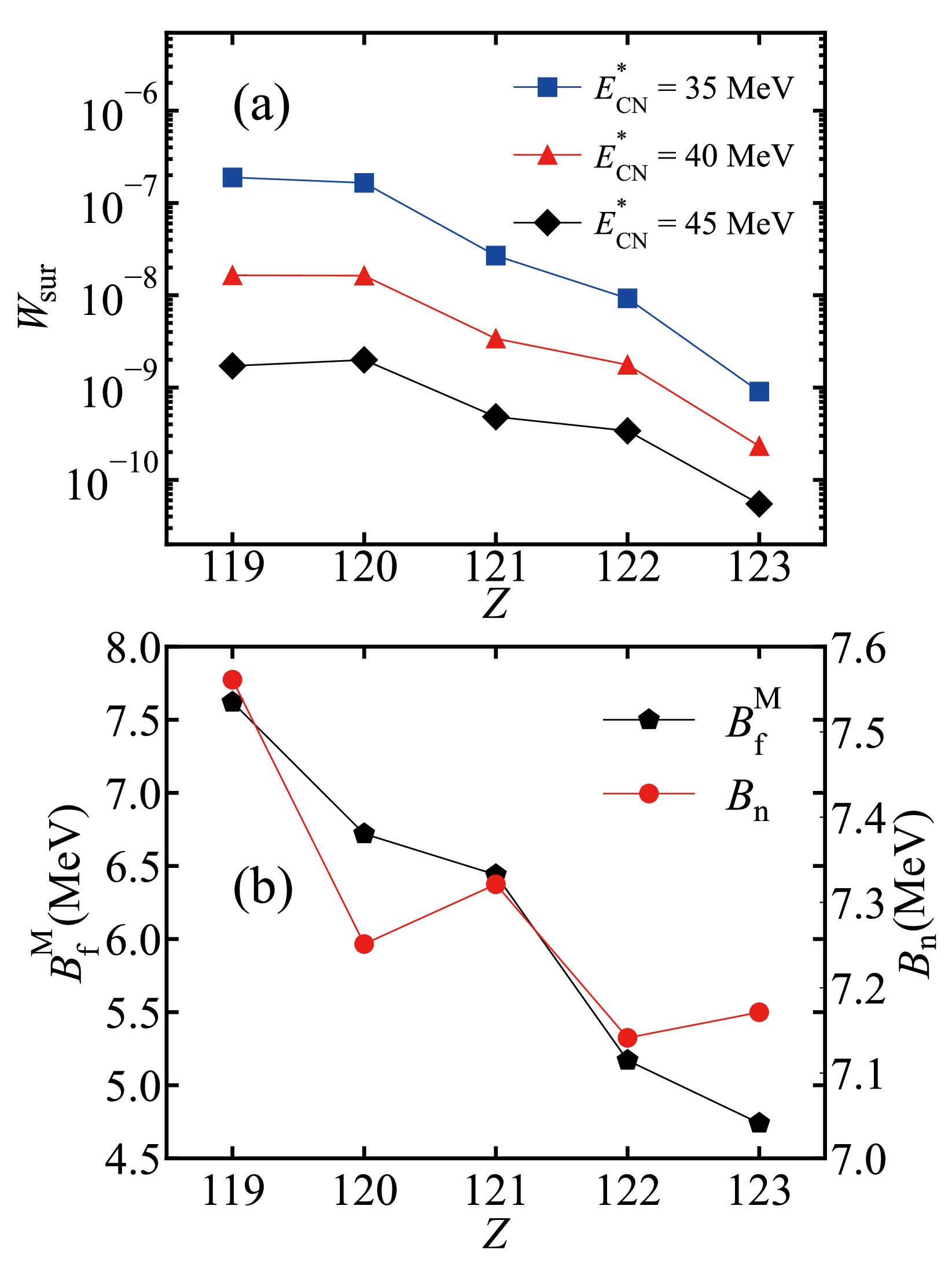
Figure 6.  (Color online) (a) The calculated fusion probabilities for the synthesis of the SHEs with Z = 119-123 via the reactions $^{45}\mathrm{Sc} + ^{252}{\rm{Cf}}$, $^{50}\mathrm{Ti} + ^{252}{\rm{Cf}}$, $^{51}\mathrm{V} + ^{252}{\rm{Cf}}$, $^{54}\mathrm{Cr} + ^{252}{\rm{Cf}}$ and $^{55}\mathrm{Mn} + ^{252}{\rm{Cf}}$ with $E^{*}_{\rm{CN}}$ = 35 MeV, 40 MeV and 45 MeV. (b) The $B_{\rm{fus}}$ values of the reactions $^{45}\mathrm{Sc} + ^{252}{\rm{Cf}}$, $^{50}\mathrm{Ti} + ^{252}{\rm{Cf}}$, $^{51}\mathrm{V} + ^{252}{\rm{Cf}}$, $^{54}\mathrm{Cr} + ^{252}{\rm{Cf}}$ and $^{55}\mathrm{Mn} + ^{252}{\rm{Cf}}$ at J = 0, 10, 20, 30.

In Fig. 7(a), the survival probabilities of the formed nuclei with Z = 119-123 at $ E^{*}_{\rm{CN}} $ = 35, 40 and 45 MeV are presented. It can be observed that the survival probability at $ E^{*}_{\rm{CN}} $ = 35 MeV is comparatively higher, exhibiting a decreasing trend with increasing $ E_{\mathrm{CN}}^{*} $. This can be attributed to the diminished stability of compound nuclei at higher excitation energies. Additionally, Fig. 7(a) reveals a decreasing trend in the survival probabilities with increasing $ Z_{\rm{CN}} $, featuring an odd-even staggering. Within the DNS model, the survival probability is determined by the competition of fission and neutron emission. This process is mainly influenced by the $ B^{\rm{M}}_{\rm{f}} $ values and the neutron separation energy $ B_{\rm{n}} $ of the formed compound nuclei, as presented in Fig. 7(b). Notably, a decreasing trend is observed in $ B^{\rm{M}}_{\rm{f}} $ values with increasing $ Z_{\rm{CN}} $, resulting in the enhanced fission probabilities and suppressed survival probabilities for compound nuclei with higher $ Z_{\rm{CN}} $. Moreover, Fig. 7(b) reveals an odd-even staggering in $ B_{\rm{n}} $ values, with reduced values for even-$ Z_{\rm{CN}} $ compound nuclei. This phenomenon contributes to an increased probability of neutron emission for compound nuclei with even $ Z_{\rm{CN}} $, thereby leading to the odd-even staggering in the survival probabilities. The combined impact of the $ B^{\rm{M}}_{\rm{f}} $ and $ B_{\rm{n}} $ values results in the decreasing trend of the survival probabilities coupled with odd-even staggering.

Figure 7.  (Color online) (a) The calculated survival probabilities of the compound nuclei with Z = 119-123 in the 3n-emission channel with $E^{*}_{\rm{CN}}$ = 35 MeV, 40 MeV and 45 MeV. (b) The $B^{\rm{M}}_{\rm{f}}$ and $B_{\rm{n}}$ values of the corresponding superheavy nuclei.

Owing to its substantial neutron excess, $ ^{252} {\rm{Cf}}$ stands out as a promising target material for approaching the predicted shell closure N = 184. Given the constrained neutron number of the stable projectiles, the application of neutron-rich radioactive beams in fusion reactions becomes necessary to reach this region. In this case, the combinations of the $ ^{252} {\rm{Cf}}$ target and corresponding radioactive projectiles with Z = 20–25 are selected. In the DNS model, the shell effects are incorporated in the de-excitation process. Nuclei with shell closure possess higher stability and are less likely to fission, and the shell effects are reflected by the increase in the fission barrier height in Eq. (20), thereby increasing their survival probability.

In evaluating the potential of radioactive beam-induced reactions, it is essential to consider both the maximal ER cross sections and the beam intensities $ I_{0} $, as the production rate is proportional to the product of these two factors, expressed as $ \psi = \sigma_{\mathrm{ER}}^{\mathrm{max}}\times I_{0} $. In Table 2, the half-lives of the radioactive projectiles, the optimal incident energies, the maximal ER cross sections, the beam intensities proposed by ATLAS [105] and the ψ values of reactions synthesizing nuclei with N = 184 are presented. It can be observed in Table 2 that not only do the maximal ER cross sections of the 3n-emission channel surpass those of the 4n and 5n-emission channels, but the half-lives and beam intensities of the corresponding radioactive nuclei are also more substantial. Consequently, the 3n-emission channel are more advantageous for reaching the region of N = 184. The reactions $ ^{53} {\rm{Ca}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{302} {\rm{Og}}$+3n (21 fb at 200.7 MeV), $ ^{54} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{303} {\rm{119}}$+3n (8.0 fb at 210.8 MeV), $ ^{55} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{304} {\rm{120}}$+3n (0.23 fb at 227.4 MeV), $ ^{56} {\rm{V}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{305} {\rm{121}}$+3n (0.034 fb at 236.9 MeV), $ ^{57} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{303} {\rm{119}}$+3n (0.0030 fb at 253.7 MeV) and $ ^{58} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{307} {\rm{123}}$+3n (0.00042 fb at 265.2 MeV) are worthy of further investigation for producing $ ^{302} {\rm{Og}}$, $ ^{303} {\rm{119}}$, $ ^{304} {\rm{120}}$, $ ^{305} {\rm{121}}$, $ ^{306} {\rm{122}}$ and $ ^{307} {\rm{123}}$.

$ \mathrm{Reaction\ Channel} $	$ T_{\mathrm{1/2}}^{\mathrm{projectile}} $ (ms)	$ E_{\mathrm{c.m.}} $ (MeV)	$ E^{*}_\mathrm{CN} $ (MeV)	$ \sigma_{\mathrm{ER}}^{\mathrm{max}} $ (fb)	$ I_{\mathrm{0}} $ p/s	ψ fb×p/s
$ ^{53} {\rm{Ca}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{302} {\rm{Og}}$+3n	$ 461 $	$ 200.7 $	$ 33.0 $	$ 2.1 ^{+2.1}_{-1.1}\times 10^{1} $	$ 5.4\times 10^{4} $	$ 1.1 ^{+1.1}_{-0.6}\times 10^{6} $
$ ^{54} {\rm{Ca}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{302} {\rm{Og}}$+4n	$ 90 $	$ 205.2 $	$ 38.0 $	$ 1.2 ^{+1.6}_{-0.7}\times 10^{1} $	$ 7.5\times 10^{3} $	$ 9.0 ^{+11.6}_{-5.3}\times 10^{4} $
$ ^{55} {\rm{Ca}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{302} {\rm{Og}}$+5n	$ 22 $	$ 209.6 $	$ 45.0 $	$ 1.3 ^{+1.7}_{-0.8}\times 10^{1} $	$ 3.6\times 10^{2} $	$ 4.7 ^{+6.1}_{-2.9}\times 10^{3} $
$ ^{54} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{303} {\rm{119}}$+3n	$ 526 $	$ 210.8 $	$ 28.0 $	$ 8.0 ^{+8.0}_{-4.4} $	$ 1.2\times 10^{6} $	$ 9.6 ^{+9.5}_{-5.2}\times 10^{6} $
$ ^{55} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{303} {\rm{119}}$+4n	$ 96 $	$ 220.9 $	$ 41.0 $	$ 2.2 ^{+2.6}_{-1.2}\times 10^{-1} $	$ 1.9\times 10^{5} $	$ 4.2 ^{+4.9}_{-2.3}\times 10^{4} $
$ ^{56} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{303} {\rm{119}}$+5n	$ 26 $	$ 225.0 $	$ 48.0 $	$ 1.6 ^{+2.1}_{-0.9}\times 10^{-1} $	$ 2.7\times 10^{4} $	$ 4.3 ^{+5.7}_{-2.4}\times 10^{3} $
$ ^{55} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{304} {\rm{120}}$+3n	$ 1300 $	$ 227.4 $	$ 33.0 $	$ 2.3 ^{+1.9}_{-1.1}\times 10^{-1} $	$ 1.6\times 10^{7} $	$ 3.7 ^{+3.1}_{-1.8}\times 10^{6} $
$ ^{56} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{304} {\rm{120}}$+4n	$ 200 $	$ 236.0 $	$ 43.0 $	$ 4.2 ^{+4.3}_{-2.0}\times 10^{-2} $	$ 2.9\times 10^{6} $	$ 1.2 ^{+1.3}_{-0.6}\times 10^{5} $
$ ^{57} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{304} {\rm{120}}$+5n	$ 95 $	$ 248.6 $	$ 58.0 $	$ 1.6 ^{+1.3}_{-0.6}\times 10^{-2} $	$ 5.3\times 10^{5} $	$ 8.5 ^{+6.9}_{-3.2}\times 10^{3} $
$ ^{56} {\rm{V}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{305} {\rm{121}}$+3n	$ 216 $	$ 236.9 $	$ 32.0 $	$ 3.4 ^{+2.6}_{-1.6}\times 10^{-2} $	$ 1.8\times 10^{8} $	$ 6.1 ^{+4.7}_{-2.9}\times 10^{6} $
$ ^{57} {\rm{V}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{305} {\rm{121}}$+4n	$ 350 $	$ 249.4 $	$ 45.0 $	$ 2.6 ^{+2.4}_{-1.1}\times 10^{-3} $	$ 3.7\times 10^{7} $	$ 9.6 ^{+4.7}_{-2.9}\times 10^{4} $
$ ^{58} {\rm{V}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{305} {\rm{121}}$+5n	$ 191 $	$ 266.0 $	$ 63.0 $	$ 8.5 ^{+5.0}_{-2.5}\times 10^{-4} $	$ 6.9\times 10^{6} $	$ 5.9 ^{+3.5}_{-1.7}\times 10^{3} $
$ ^{57} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{306} {\rm{122}}$+3n	$ 21100 $	$ 253.7 $	$ 37.0 $	$ 3.0 ^{+1.7}_{-1.2}\times 10^{-3} $	$ 1.0\times 10^{9} $	$ 3.0 ^{+1.7}_{-1.2}\times 10^{6} $
$ ^{58} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{306} {\rm{122}}$+4n	$ 7000 $	$ 271.0 $	$ 54.0 $	$ 5.3 ^{+2.5}_{-1.0}\times 10^{-4} $	$ 4.0\times 10^{8} $	$ 2.1 ^{+1.0}_{-0.5}\times 10^{5} $
$ ^{59} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{306} {\rm{122}}$+5n	$ 1050 $	$ 271.0 $	$ 54.0 $	$ 5.3 ^{+2.5}_{-1.0}\times 10^{-4} $	$ 1.0\times 10^{8} $	$ 5.3 ^{+2.5}_{-1.0}\times 10^{4} $
$ ^{58} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{307} {\rm{123}}$+3n	$ 3000 $	$ 265.2 $	$ 38.0 $	$ 4.2 ^{+2.0}_{-1.4}\times 10^{-4} $	$ 1.0\times 10^{9} $	$ 4.2 ^{+2.0}_{-1.0}\times 10^{5} $
$ ^{59} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{307} {\rm{123}}$+4n	$ 4590 $	$ 288.8 $	$ 61.0 $	$ 4.6 ^{+0.8}_{-0.5}\times 10^{-5} $	$ 1.0\times 10^{9} $	$ 4.6 ^{+0.8}_{-0.5}\times 10^{4} $
$ ^{60} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ $ \rightarrow $ $ ^{307} {\rm{123}}$+5n	$ 280 $	$ 306.8 $	$ 79.0 $	$ 2.8 ^{+0.2}_{-0.1}\times 10^{-5} $	$ 1.0\times 10^{9} $	$ 2.8 ^{+0.2}_{-0.1}\times 10^{4} $

Table 2.  The radioactive beam-induced reactions with $ ^{252} {\rm{Cf}}$ target for producing the superheavy nuclei with $ N = 184 $. The reaction channels, the half-lives of corresponding projectiles [104], the optimal incident energies $ E_{\mathrm{c.m.}} $, the corresponding excitation energies $ E^{*}_{\mathrm{CN}} $ and the maximal ER cross sections $ \sigma_{\mathrm{ER}}^{\mathrm{max}} $ are listed in columns 1-5, respectively. The beam intensities $ I_{0} $ [105] and the corresponding ψ values are listed in columns 6-7.

In Fig. 8, the predicted ER cross sections of these six reactions are plotted. It illustrates an exponential decrease in the maximal ER cross section as the charge number of the projectile increases. The maximal ER cross sections range from 21 fb to 0.00042 fb, falling well below the detection limitation (approximately 0.1 pb). Taking into account the beam intensities, the reactions $ ^{54}\mathrm{Sc} + ^{252} {\rm{Cf}}$ and $ ^{56}\mathrm{V} + ^{252} {\rm{Cf}}$ exhibit relatively large ψ values of 9.6$ \times10^{6} $ fb$ \times $p/s and 6.1$ \times10^{6} $ fb$ \times $p/s. Considering experimental feasibility, the reactions $ ^{55}\mathrm{Ti} + ^{252} {\rm{Cf}}$ and $ ^{57}\mathrm{Cr} + ^{252} {\rm{Cf}}$ emerge as better options, with the half-lives for the corresponding projectiles to be 1.2 s and 21.1 s, along with the ψ values to be 3.7$ \times10^{6} $ fb$ \times $p/s and 3.0$ \times10^{6} $ fb$ \times $p/s.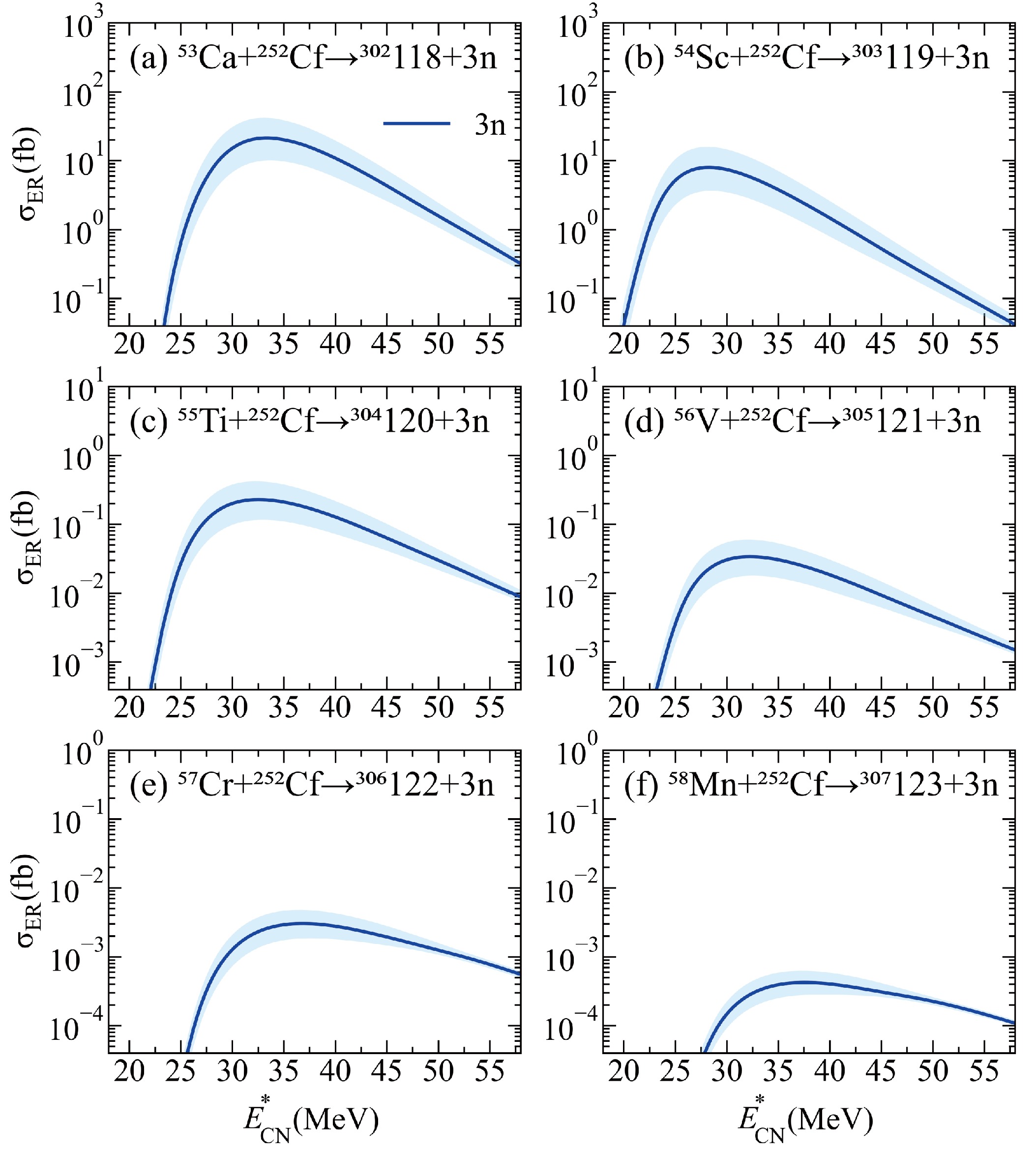

Figure 8.  (Color online) The predicted ER cross sections of the reactions $^{53}\mathrm{Ca} + ^{252}{\rm{Cf}}$ $\rightarrow$ $^{302}{\rm{118}}+{\rm{3n}}$ (a), $^{54}\mathrm{Sc} + ^{252}{\rm{Cf}}$ $\rightarrow$ $^{303}{\rm{119}}+{\rm{3n}}$ (b), $^{55}\mathrm{Ti} + ^{252}{\rm{Cf}}$ $\rightarrow$ $^{304}120+{\rm{3n}}$ (c), $^{56}\mathrm{V} + ^{252}{\rm{Cf}}$ $\rightarrow$ $^{305}{\rm{121}}+{\rm{3n}}$ (d), $^{57}\mathrm{Cr} + ^{252}{\rm{Cf}}$ $\rightarrow$ $^{306}{\rm{122}}+{\rm{3n}}$ (e) and $^{58}\mathrm{Mn} + ^{252}{\rm{Cf}}$ $\rightarrow$ $^{307}{\rm{123}}+{\rm{3n}}$ (f). The calculation uncertainties are given by the shaded areas.

In Fig. 9, the superheavy nuclei region (Z $ \geq $ 114) at the top-right part of the nuclear chart is presented. The predicted ER cross sections of the unknown isotopes with Z = 118-123 are summarized in this figure. The results suggest that synthesizing superheavy nuclei with Z = 119-123 using stable beams and $ ^{252} {\rm{Cf}}$ target is tough with present experimental facility. The synthesis of new superheavy nuclei via stable beam-induced reactions is constrained by the limited neutron number of the projectile, resulting in the limited neutron number of the synthesized nuclei. Consequently, radioactive beam-induced reactions present an alternative approach for the synthesis of neutron-rich superheavy nuclei, offering comparable ER cross sections.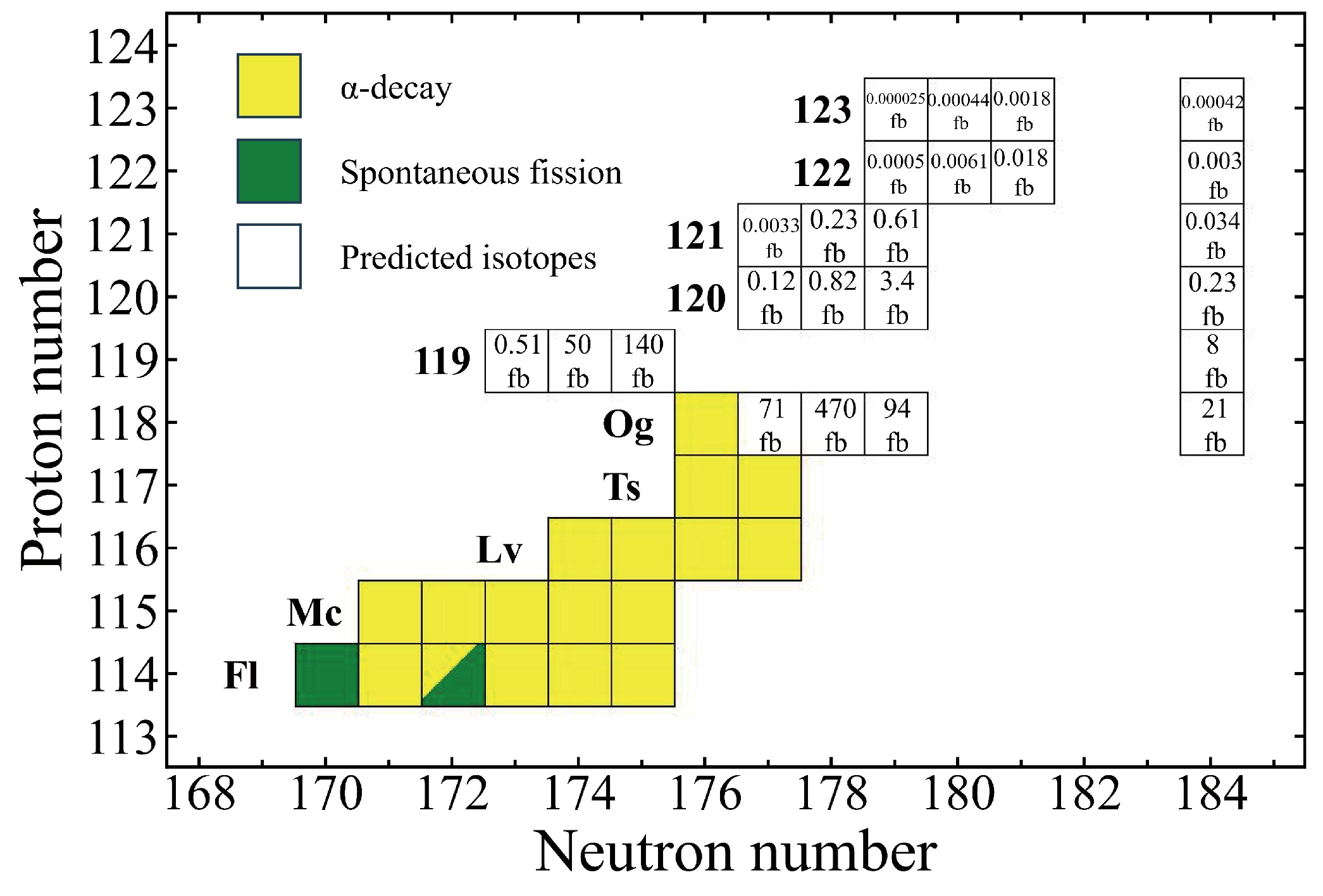

Figure 9.  (Color online) The superheavy nuclei region with Z $\geq$ 114 at the top-right part of the nuclear map. The known and predicted nuclei are marked by the filled and open squares, respectively. The α decay and spontaneous fission are indicated by the colors yellow and olive, respectively.

The synthesis of superheavy nuclei with N = 184 using radioactive beams with Z = 20-25 and $ ^{252} {\rm{Cf}}$ target is similarly challenging. However, with anticipated advancements in beam intensities and detection efficiency, the potential to expand the nuclear chart boundaries and approach the predicted closed neutron shell using $ ^{252} {\rm{Cf}}$ target remains promising. Considering the decreasing trend observed in ER cross sections as the proton number of the projectile increases, lighter radioactive beams emerge as an alternative option for synthesizing new neutron-rich superheavy nuclei.

In this paper, the reliability of the DNS model is examined with the experimental results of the reactions $ ^{48} {\rm{Ca}}$+$ ^{245,248} {\rm{Cm}}$, $ ^{249} {\rm{Bk}}$ and $ ^{249} {\rm{Cf}}$. Based on the neutron-rich actinide target $ ^{252} {\rm{Cf}}$, the fusion reactions synthesizing new superheavy nuclei with Z = 118-123 are investigated. Our study reveals that the new isotopes $ ^{297} {\rm{Og}}$, $ ^{296} {\rm{Og}}$ and $ ^{295} {\rm{Og}}$ can be produced via the reaction $ ^{48}\mathrm{Ca} $+$ ^{252} {\rm{Cf}}$ with maximal ER cross sections of 94,470 and 71 fb, respectively. The 3n-emission channels of the reactions $ ^{45} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$, $ ^{50} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$, $ ^{51} {\rm{V}}$+$ ^{252} {\rm{Cf}}$, $ ^{54} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$, $ ^{55} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ are worthy of further investigation to synthesize new elements with Z = 119-123. The maximal ER cross sections, along with optimal incident energies are predicted to be 140 fb (204.0 MeV), 0.61 fb (234.5 MeV), 0.018 fb (249.8 MeV), 0.0018 fb (259.6 MeV), respectively. The maximal ER cross sections have an exponential decreasing trend with the increasing proton number of the compound nucleus, coupled with a corresponding rise in optimal incident energies. Furthermore, the impact of various factors, including the Q value, the Coulomb barrier, the inner fusion barrier, the neutron separation energy and the fission barrier are discussed on the capture, fusion and survival stages, respectively.

Additionally, the radioactive beam-induced reactions with the $ ^{252} {\rm{Cf}}$ target are investigated to achieve the predicted neutron shell closure N = 184. The reactions $ ^{53} {\rm{Ca}}$+$ ^{252} {\rm{Cf}}$, $ ^{54} {\rm{Sc}}$+$ ^{252} {\rm{Cf}}$, $ ^{55} {\rm{Ti}}$+$ ^{252} {\rm{Cf}}$, $ ^{56} {\rm{V}}$+$ ^{252} {\rm{Cf}}$, $ ^{57} {\rm{Cr}}$+$ ^{252} {\rm{Cf}}$ and $ ^{58} {\rm{Mn}}$+$ ^{252} {\rm{Cf}}$ are predicted to be favorable for producing superheavy nuclei with N = 184. The maximal ER cross sections (the optimal incident energies) are 21 fb (200.7 MeV), 8.0 fb (210.8 MeV), 0.23 fb (227.4 MeV), 0.034 fb (236.9 MeV), 0.0030 fb (253.7 MeV) and 0.00042 fb (265.2 MeV). The predicted results fall below the current detection limitation, requiring the advancement in the beam intensity and detection techniques in future experiments.